Devoir n° 31 - 2nd s

Classe: 
Seconde

Exercice 1 

1) Soit $E=\sqrt{98}-3\sqrt{2}-2\sqrt{45}$
 
a) Montrer que $E=4\sqrt{2}-6\sqrt{5}$
 
b) Montrer que $E<0$
 
2) Soit $F=-3\sqrt{2}-5\sqrt{5}$
 
a) Montrer que $E-F=7\sqrt{2}-\sqrt{5}$
 
b) Comparer $7\sqrt{2}$ et $\sqrt{5}$
 
c) En déduire une comparaison de $E$ et $F$
 
d) Comparer $E^{2}$ et $F^{2}$
 
3) Calculer $A$ en donnant le résultat sous la forme d'une fraction irréductible : $$A=\dfrac{1}{3}+\dfrac{5}{4}\times\dfrac{7}{3}-\dfrac{1}{2}$$

Exercice 2 

1) Calculer $C=|2\pi-7|+|\sqrt{5}-2|-(\sqrt{5}-2\pi+5)$
 
2) Soient $a\in\mathbb{R}^{+}$ et $b\in\mathbb{R}^{-}.$ Simplifier : $$\sqrt{64a^{2}b^{2}}-5a\sqrt{b^{2}}+5b\sqrt{4a^{2}}$$
3) On donne les ensembles : 
 
$E=\{x\in\mathbb{R}\;;\ 2\leq x\leq 5\}$ et $E=\{y\in\mathbb{R}\;;\ -3\leq y\leq -1\}$
 
a) Écrire $E$ et $F$ sous forme d'intervalles.
 
b) Donner un encadrement de $(-3x)\;;\ x^{2}\;;\ (-y)$ et $(-xy)$

Exercice 3 

Soit $a$ un angle aigu. Montrer que :
 
1) $(\cos^{2}a+\sin^{2}a)(\cos^{2}a-\sin^{2}a)=1-2\sin^{2}a$
 
2) $\tan a+\dfrac{1}{\tan a}=\dfrac{1}{\cos a\sin a}$

Exercice 4 

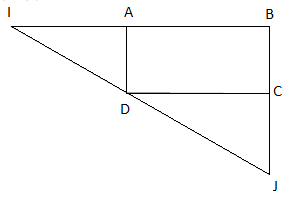
Dans la figure ci-dessous (qui n'est pas en vraie grandeur) on donne : $ABCD$ un rectangle tels que $AB=6\;;\ AD=2$ et $AI=4.$
La droite $(BC)$ coupe $(DI)$ en un point $J.$
 
1) a) Montrer que $BJ=5$
 
b) En déduire que $CJ=3$ et $DJ=3\sqrt{5}$
 
2) a) Calculer $\tan(\widehat{AID})$
 
b) Donner une valeur approchée à $10^{-3}$ près de $(\widehat{AID})$
 
3) Soit $H$ le projeté orthogonal de $C$ sur $(DJ)$
 
a) Montrer que $CH=\dfrac{6\sqrt{5}}{5}$
 
b) Calculer $\cos(\widehat{DCH}).$ En déduire $\sin(\widehat{DCH})$ et $\tan(\widehat{DCH})$

 
$$\text{Durée : 3 h}$$
 
 
Auteur: 
Mouhamadou Ka

Commentaires

Anonyme (non vérifié)

dim, 01/08/2023 - 14:56

Très bien

Anonyme (non vérifié)

dim, 01/08/2023 - 14:56

Très bien

Ajouter un commentaire