Droites perpendiculaires et droites parallèles - 6e
Classe:
Sixième
I. Droites perpendiculaires
I.1. Présentation
Deux droites perpendiculaires sont deux droites sécantes en formant un angle droit.
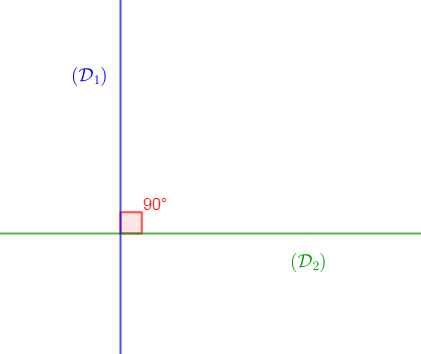
Les droites $(\mathcal{D}_{1})$ et $(\mathcal{D}_{2})$ sont perpendiculaires
On note : $(\mathcal{D}_{1})\perp(\mathcal{D}_{2})$
On lit : la droite $(\mathcal{D}_{1})$ est perpendiculaire à la droite $(\mathcal{D}_{2})$
I.2. Construction
I.2.1. La règle et l'équerre
On trace la droite $(\mathcal{D}_{1})$ avec la règle.
On pose un coté de l'angle droit de l'équerre sur $(\mathcal{D}_{1})$
On trace la droite $(\mathcal{D}_{2})$ sur l'autre coté de l'angle droit de l'équerre :
On prolonge $(\mathcal{D}_{2})$ par la règle et on met le codage
I.1.2 La règle et le compas
On trace la droite $(\mathcal{D}_{1})$ avec la règle
On choisit deux points distincts sur $(\mathcal{D}_{1})$
A partir de chaque point; on trace un arc de cercle qui dépasse le milieu du segment formé par les deux points.
On trace la droite $(\mathcal{D}_{2})$passant par les deux points formés par les intersections des deux arcs.
On a : $(\mathcal{D}_{1})\perp(\mathcal{D}_{2})$ et on met le codage.
I.3. Propriété
Activité
Tracer une droite $(\mathcal{D})$ puis placer un point $A$ n'appartenant pas $(\mathcal{D}).$
Tracer la droite $(\mathcal{D'})$ passant par $A$ tel que : $(\mathcal{D}')\perp(\mathcal{D}).$
Combien peut-on tracer de droites $(\mathcal{D'})$ passant par $A$ ?
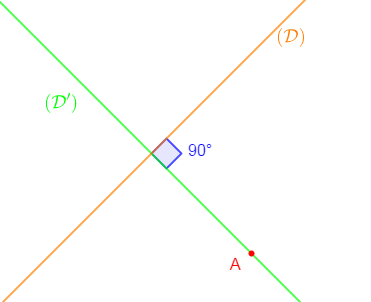
Énoncé
Par un point du plan passe une et une seule droite perpendiculaire à une droite donnée.
I.4. Médiatrice d'un segment
Activité
Soit $[AB]$ un segment du plan et $O$ son milieu.
Tracer la droite $(\mathcal{D})$ passant par $O$ et perpendiculaire à $(AB).$
Que représente $(\mathcal{D})$ pour $[AB]$ ?
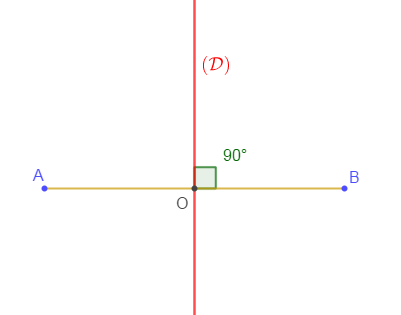
Définition
Une médiatrice d'un segment est une droite qui passe par le milieu de ce segment et perpendiculaire au support de ce segment.
Traduction mathématique
$\mathcal{(D)}$ est la médiatrice de $[AB]$ signifie que $\mathcal{(D)}$ passe par le milieu de $[AB]$ et est perpendiculaire à $(AB).$
Propriété 1
Tout point de $\mathcal{(D)}$ est situé à égale distance des extrémités de ce segment.
Propriété 2
Tout point situé à égale distance des extrémités d'un segment appartient à la médiatrice de ce segment.
I.5. Hauteur d'un triangle
La hauteur d'un triangle est la droite qui passe par un sommet et perpendiculaire au support du coté opposé à ce sommet.
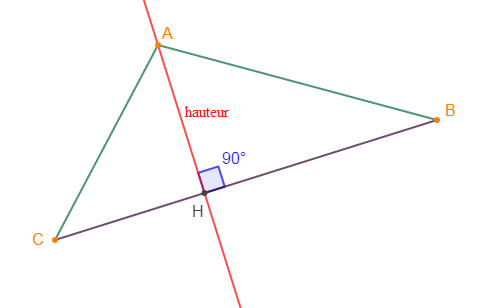
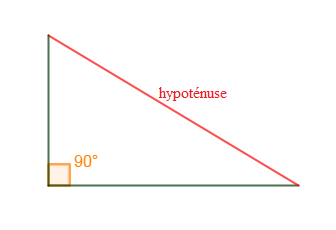
I.6. Triangle rectangle
Un triangle rectangle est un triangle dont les supports de deux cotés sont perpendiculaires.
Le troisième coté opposé à l'angle droit est appelé l'hypoténuse.
II. Droites parallèles
II.1. Présentation
Activité
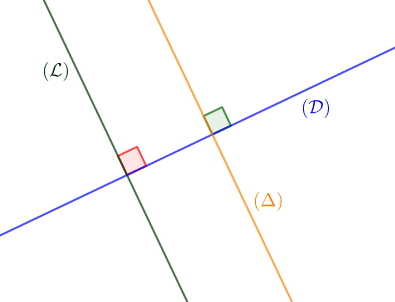
Soit $\mathcal{(D)}$ une droite du plan. Tracer la droite $\mathcal{(L)}$ perpendiculaire à $\mathcal{(D)}$ puis la droite $(\Delta)$ perpendiculaire à $\mathcal{(D)}.$
Que peut-on dire des droites $\mathcal{(L)}$ et $(\Delta)$ ?
Définition
Deux droites sont parallèles lorsqu'elles sont perpendiculaires à une même droite.
On écrit : $\mathcal{(L)}\parallel(\Delta)$.
On lit : la droite $\mathcal{(L)}$ est parallèle à la droite $(\Delta)$.
Traduction mathématique
Données : $\mathcal{(L)}\perp\mathcal{(D)}\ $ et $\ (\Delta)\perp\mathcal{(D)}$
Conclusion : $\mathcal{(L)}\parallel(\Delta)$
II.2. Construction
II.2.1. La règle et l'équerre
On trace la droite $(\Delta)$ avec la règle et on place un point $A$ n'appartenant pas à $(\Delta).$
On pose un coté de l'angle droit de l'équerre sur $(\Delta)$ et sur l'autre côté de l'angle droit, on place la règle.
En maintenant une légère pression sur la règle, on fait glisser l'équerre jusqu'au point $A.$
On retire la règle et on trace la droite $(\mathcal{L})$ passant par $A.$
On prolonge $(\mathcal{L})$ par la règle et on met le codage
II.2.2. La règle et le compas
On trace la droite $(\Delta)$ avec la règle
On choisit deux points distincts $A\ $ et $\ B$ sur $(\Delta)$
A partir de chaque point ; on trace un arc de cercle de rayon la longueur du segment $[AB].$
Ensuite, on prend comme centre le point $A$ et avec le compas on trace un arc de cercle qui coupe le premier arc au point $C.$
Après, on passe en $B$, en conservant la même ouverture $AC$ et on place le point $D.$
Enfin, on trace la droite $(\mathcal{L})$ passant par les deux points $C\ $ et $\ D.$
On a : $(\mathcal{L})\parallel(\Delta)$ et on met le codage.
II.3. Propriétés
Activité
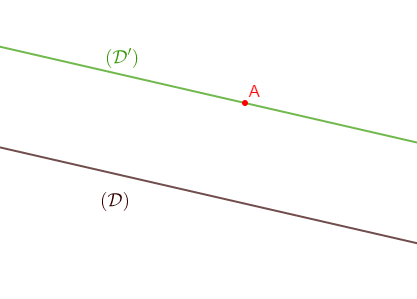
Soient $\mathcal{(D)}$ une droite du plan et $A$ un point n'appartenant pas à $\mathcal{(D)}.$
Tracer la droite $\mathcal{(D')}$ passant par $A$ et parallèle à $\mathcal{(D)}.$
Combien y a-t-il de possibilités ?
Propriété 1
Par un point du plan,passe une droite et une seule parallèle à une droite donnée.
Activité
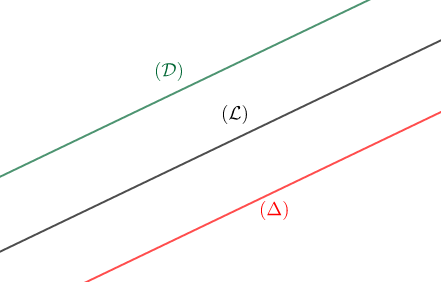
Soient $\mathcal{(L)}$ et $(\Delta)$ deux droites parallèles.
Tracer la droite $\mathcal{(D)}\parallel\mathcal{(L)}.$
Quelle est la position de $\mathcal{(D)}$ par rapport à $(\Delta)$ ?
Propriété 2
Deux droites étant parallèles;toute droite parallèle à l'une est parallèle à l'autre.
Traduction mathématique
Données : $\mathcal{(L)}\parallel(\Delta)\ $ et $\ \mathcal{(L)}\parallel\mathcal{(D)}$
Conclusion : $(\Delta)\parallel\mathcal{(D)}$
Propriété 3
Lorsque deux droites sont parallèles;toute droite perpendiculaire à l'une est perpendiculaire à l'autre.
Traduction mathématique
Données : $\mathcal{(L)}\parallel(\Delta)\ $ et $\ \mathcal{(L)}\perp\mathcal{(D)}$
Conclusion : $(\Delta)\perp\mathcal{(D)}$

Commentaires
Zeynabou (non vérifié)
mar, 04/27/2021 - 01:41
Permalien
Je peux avoir des cours en
Mariama Hadjara... (non vérifié)
mar, 03/01/2022 - 21:52
Permalien
Moi aussi j'aimerais avoir
Mariama Hadjara... (non vérifié)
mar, 03/01/2022 - 21:54
Permalien
J'aimerais aussi avoir des
Ajouter un commentaire