Vous êtes ici

Exercices d'entraînement types du Bac : Dénombrement - Probabilités

Classe:

Terminale

I. Calcul avec des factorielles ou des $\dbinom{n}{p}$

Exercice 1

Simplifier les expressions suivantes :

$\dfrac{21!}{19!}$

$\dfrac{15!(4!)^{2}}{3!5!16!}$

$\dfrac{(n-1)!(n+1)!}{(n!)^{2}}$

$\dfrac{1}{(n+1)!}+\dfrac{1}{(n-1)!}$

Exercice 2

Soit

$\varphi_{n}$ la fonction définie par

$\varphi_{n}(x)=(x+1)^{n}$ ,

$\ n$ étant un entier naturel.

1) Développer l'expression

$\varphi_{n}(x)$ .

2) En déduire les sommes

$\sum_{p=0}^{n}\dbinom{n}{p}\quad\text{et}\quad\sum_{p=0}^{n}(-1)^{p}\dbinom{n}{p}$

3) Déduire de deux écritures de la dérivée de la fonction

$\varphi_{n}$ la formule remarquable :

$\dbinom{n}{1}+2\dbinom{n}{2}+3\dbinom{n}{3}+\cdots+n\dbinom{n}{n}=\sum_{k=1}^{n}k\dbinom{n}{k}=n\cdot 2^{n-1}$

Exercice 3

1) Démontrer les égalités suivantes :

$p\dbinom{n}{p}=n\dbinom{n-1}{p-1}$

$p(p-1)\dbinom{n}{p}=n(n-1)\dbinom{n-2}{p-2}$

2) En remarquant que

$(1+x)^{n}\times(1+x)^{n}=(1+x)^{2n}$ , démontrer que

$\dbinom{n}{0}^{2}+\dbinom{n}{1}^{2}+\cdots+\dbinom{n}{n}^{2}=\dbinom{2n}{n}$

Exercice 4

1) Développer les binômes suivants :

$(2x-3y)^{7}$

$(2+\mathrm{i})^{6}$

$\left(x^{3}\sqrt{2}-\dfrac{1}{x\sqrt{2}}\right)^{4}$

2) Quel est le coefficient de

$x^{4}y^{3}$ dans le développement de

$(2x-3y)^{7}.$

Exercice 5

Résoudre dans

$\mathbb{N}$ les équations suivantes :

$n!=48-6n$

$\dbinom{n}{5}=\dbinom{n}{7}$

$\dbinom{n}{3}-\dbinom{n}{2}=5+\dfrac{n^{3}-6n^{2}}{6}$

II. Dénombrement

Exercice 1

Combien y a-t-il de nombres à 4 chiffres tel que le chiffre des milliers soit impair, le chiffre des centaines strictement inférieur à 7, le chiffre des dizaines pair et le chiffre des unités supérieur ou égal à 4 ?

Exercice 2

Un lycée de 1200 élèves (640 filles et 560 garçons) et de 180 professeurs (72 femmes et 108 hommes) veut se doter d'un conseil de 10 membres, 5 élèves et 5 professeurs. De combien de façons peut-on procéder si

a) on n'impose pas de condition particulière ?

b) on veut que le conseil ait autant de membres masculins que féminins ?

c) on veut que le conseil ait au moins 4 filles et au moins 4 membres masculins ?

Exercice 3

De combien de manières peut-on choisir 2 délégués de nationalités différentes parmi 4 belges, 6 français et 8 anglais ?

Exercice 4

De combien de manières une société de 10 membres peut-elle choisir un groupe de 3 personnes pour effectuer un voyage culturel

a) si Madame Gamma refuse de partir avec Monsieur Zète ?

b) si Mlle Alpha et M. Bêta n'acceptent de participer au voyage que s'ils sont ensemble ?

c) si on est soumis aux deux contraintes précédentes à la fois ?

d) mêmes questions si on veut constituer un groupe de 4 personnes pour le voyage.

Exercice 5

Une compagnie aérienne doit desservir 6 villes, chacune étant reliée, sans escale, à chacune des autres.

a) Combien de lignes la compagnie met-elle en service ?

b) Quel serait le nombre de lignes si la compagnie desservait 12 villes ?

Exercice 6

B. a 5 livres d'algèbre, 3 livres de géométrie et 4 livres d'analyse.

a) De combien de manières peut-il les ranger sur une étagère de sa bibliothèque ?

b) Même question en les regroupant par sujet.

Exercice 7

De combien de façons peut-on ranger 5 boules dans 7 cases

a) si les boules et les cases sont discernables, chaque case ne pouvant recevoir qu'une seule boule ?

b) si les boules et les cases sont discernables, chaque case pouvant recevoir un nombre quelconque de boules ?

c) si les boules sont indiscernables, les cases sont discernables, chaque case ne pouvant recevoir qu'une seule boule ?

d) si les boules sont indiscernables, les cases sont discernables, chaque case pouvant recevoir un nombre quelconque de boules ?

Exercice 8

On lance deux dés sur une table. L'un cubique et ses faces sont numérotées de 1 à 6, l'autre est tétraédrique et ses quatre faces sont numérotées de 1 à 4.

Combien y a t-il de résultats possibles si l'on considère toujours en premier le résultat du dé cubique ?

Exercice 9

Un élève se présente à l'examen oral avec 12 leçons d'histoire étudiées dont 9 sont sues, 10 leçons de géographie étudiées dont 7 sont sues. Il doit tirer une leçon d'histoire et une leçon de géographie et traiter les deux sujets à la fois.

1) Déterminer le nombre de choix possibles.

2) Déterminer le nombre de choix dans chacun des cas suivants :

A = "l'élève sait traiter les deux sujets"

B = "l'élève sait traiter exactement 1 sujet"

C = "l'élève ne sait traiter aucun sujet"

D = "l'élève sait traiter au moins 1 sujet"

E = "l'élève sait traiter au plus 1 sujet"

Exercice 10

Dans une classe de 35 élèves, 20 élèves pratiquent le Basket-ball, 15 élèves pratiquent le Foot-ball. Sachant qu'il y a 2 élèves qui ne pratiquent aucun de ces deux sports, déterminer :

1) le nombre d'élèves qui pratiquent exactement 1 sport.

2) le nombre d'élèves qui pratiquent au plus 1 sport.

Exercice 11

5 garçons et 6 filles désirent former une équipe de volley-ball. Le nombre de joueurs sur le terrain est de 6.

a) Combien y a t-il d'équipes possibles ?

b) Combien y a t-il d'équipe composées de 2 garçons et de 4 filles ?

Exercice 12

Avec les 9 chiffres distincts de 0, combien peut-on écrire de nombres de 5 chiffres différents

a) qui se terminent par 7 ?

b) qui se terminent par 23 ?

c) qui comprennent 4 ?

d) qui ne comprennent pas 9 ?

e) qui ne comprennent que des chiffres impairs ?

f) qui comprennent 5 mais pas 6 ?

g) qui comprennent 2 et 5 sous la forme 25 ? (p,ex. 72518, mais pas 72158)

h) qui comprennent 2 et 5 dans cet ordre ? (p.ex. 924751, mais pas 954721)

i) qui comprennent 2 et 5 dans un ordre quelconque ?

j) dont deux sont pairs et trois impairs ?

Exercice 13

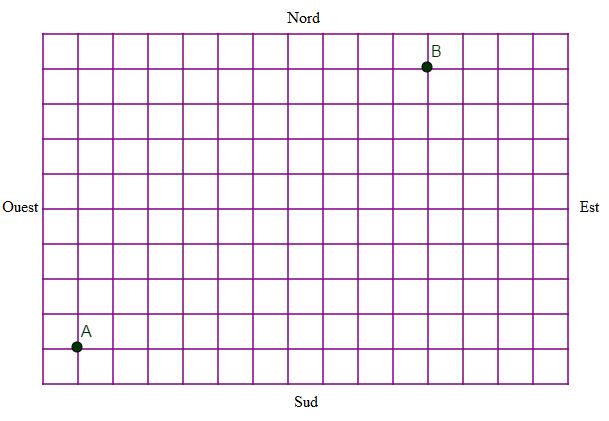
Le quadrillage ci-dessous représente le plan d'une ville moderne. Dans cette partie, la circulation n'est autorisée que vers l'est et vers le nord.

Combien existe-t-il de trajets possibles pour se rendre du point

$A$ au point

$B\ ?$

III. Probabilités

Exercice 1

Une commission européenne est formée de 20 membres : 12 allemands, 6 polonais et 2 hongrois. En en choisissant 2 au hasard, quelle est la probabilité qu'ils aient la même nationalité ?

Exercice 2

Dans une classe il y a 17 filles et 15 garçons, 8 filles ont plus de 17 ans et 10 garçons ont plus de 17 ans.

On choisit au hasard 4 élèves de la classe.

1) Quel est le nombre de choix possibles ?

2) Quelle est la probabilité des événements suivants :

$A$ : "les 4 élèves sont des garçons".

$B$ : "les 4 élèves sont de même sexe".

$C$ : "parmi les 4 élèves il y a des filles et des garçons".

$D$ : "parmi les 4 élèves il y a exactement 1 fille".

$E$ : "parmi les 4 élèves il y a au moins une fille".

$F$ : "parmi les 4 élèves il y a exactement deux élèves de plus de 17 ans".

$G$ : "parmi les 4 élèves il y a exactement 1 fille et exactement deux élèves de plus de 17 ans".

$H$ : "parmi les 4 élèves il y a exactement 1 fille ou exactement deux élèves de plus de 17 ans".

3) Déterminer les probabilités

$p_{A}(F)\;,\ p(A\cap B)$ et

$p_{F}(A)$ .

Les événements

$A$ e

$F$ sont-ils incompatibles ? Sont-ils indépendants ?

Exercice 3

Dans un village il y a 6 bistrots. Six villageois décident, sans se concerter, de passer la soirée dans un des 6 bistrots.

a) Quelle est la probabilité pour que les six personnes aient choisi le même bistrot ?

b) Quelle est la probabilité pour qu'au moins deux personnes aient choisi le même établissement ?

Exercice 4

Pour l'examen oral de géographie, le professeur a réalisé 60 fiches proposant chacune un paragraphe de la matière à réviser. Chaque élève doit en tirer 4 au hasard. Sachant que P. n'a révisé qu'un tiers du programme, quelle est la probabilité pour qu'il :

a) connaisse les 4 sujets tirés ?

b) ne connaisse aucun des 4 sujets tirés ?

c) connaisse 3 des 4 sujets tirés ?

d) rate son examen ?

Exercice 5

Dans un sac il y a 9 boules numérotées de 1 à 9. Calculez la probabilité de tirer

1) deux boules impaires

a) simultanément

b) successivement (sans remise)

2) une paire et une impaire

a) simultanément

b) successivement (sans remise)

Exercice 6

On tire simultanément 3 boules d'une urne qui contient 5 boules rouges, 3 boules blanches et 7 boules noires. Quelle est la probabilité d'obtenir :

a) 1 boule de chaque couleur ?

b) 3 boules de même couleur ?

c) 2 boules rouges et 1 boule d'une autre couleur ?

d) au moins 2 boules noires ?

Exercice 7

Jouer au loto consiste à choisir 6 numéros parmi 49. Calculez la probabilité d'avoir :

a) les 6 bons numéros.

b) 5 bons numéros et le numéro complémentaire.

c) 5 bons numéros.

d) 4 bons numéros.

e) 3 bons numéros.

Exercice 8

Une tombola comprend 1000 billets pour 2 lots gagnants. Quel est le nombre minimal de billets qu'il faut acheter pour que la probabilité de gagner soit supérieure à 0.5 ?

Exercice 9

Une urne

$U_{1}$ contient 5 boules vertes et 3 jaunes, indiscernables au toucher.

Une urne

$U_{2}$ contient 3 boules vertes, 2 jaunes et 1 orange, indiscernables au toucher.

$U_{1}$ et

$U_{2}$ ont même apparence.

On tire au hasard 2 boules de

$U_{1}$ . Si elle sont de même couleur, on les installe dans

$U_{2}$ , puis on tire au hasard 2 boules de

$U_{2}$ .

Sinon on met la boule jaune (tirée de

$U_{1}$ ) dans

$U_{2}$ , puis on tire au hasard 2 boules de

$U_{2}$ .

1) Montrer que les trois événements

$\overline{E}\;,\ E_{1}$ et

$E_{2}$ forment une partition de l'univers où

$\overline{E}\;,\ E_{1}$ et

$E_{2}$ sont les événements définis par :

$E$ : "les 2 boules tirées de

$U_{1}$ sont de même couleur" ;

$E_{1}$ : "les 2 boules tirées de

$U_{1}$ sont vertes" ;

$E_{2}$ : "les 2 boules tirées de

$U_{1}$ sont jaunes".

2) Calculer les probabilités des événements suivants :

$A$ : "les 2 boules tirées de

$U_{2}$ sont vertes" ;

$B$ : "les 2 boules tirées de

$U_{2}$ sont de même couleur".

3) Calculer la probabilité que les 2 boules tirées de

$U_{1}$ soient de même couleur sachant que les 2 boules tirées de

$U_{2}$ sont vertes.

Exercice 10

Une urne

$U_{1}$ contient 2 boules vertes et 3 rouges, indiscernables au toucher.

Une urne

$U_{2}$ contient 5 boules rouges et 3 jaunes, indiscernables au toucher.

$U_{1}$ et

$U_{2}$ ont même apparence.

On tire au hasard 2 boules de l'une de ces deux urnes.

1) Calculer les probabilités des événements suivants :

$E_{1}$ : "on tire 2 boules de

$U_{1}$ " ;

$E_{2}$ : "on tire 2 boules de

$U_{2}$ " ;

$A$ : "les boules tirées sont rouges" ;

$B$ : "les boules tirées sont jaunes" ;

$C$ : "les boules tirées sont de couleurs différentes".

2) Calculer la probabilité de l'événement "les boules tirées sont de

$U_{1}$ " sachant qu'elles sont rouges.

Exercice 11

On jette un dé à 6 faces 8 fois de suites.

On note

$X=k$ l'événement "on a obtenu

$k$ fois le

$n^{o}4$ ".

1) Quelles valeurs peut prendre

$k$ ? Cet ensemble est noté

$X(\Omega)$ .

2) Calculer

$p(X=0)\;,\ p(X=8)\;,\ p(X=1)\;,\ p(X=k)$ pour tout

$k$ de

$X(\Omega)$ puis

$P_{X\geq 4}(X=6)$ .

Exercice 12

Dans cet exercice

$n\in\mathbb{N}$ et

$n\geq 2$ .

Une urne

$U_{1}$ contient 3 boules rouges et 5 boules vertes, indiscernables au toucher.

Une urne

$U_{2}$ contient

$n$ boules rouges, 3 vertes et 2 blanches, indiscernables au toucher.

On tire au hasard 1 boule de

$U_{1}$ , puis on la jette dans

$U_{2}$ . On tire ensuite au hasard 2 boules de

$U_{2}$ .

Si on tire 2 boules rouges de

$U_{2}$ , on gagne 5 euros.

Si on tire 2 boules vertes de

$U_{2}$ , on gagne 2 euros.

Si on tire 2 boules blanches de

$U_{2}$ , on gagne 1 euro.

Si on tire 2 boules de couleurs différentes de

$U_{2}$ , on perd 2 euros.

Soit

$X$ la variable aléatoire "gain en euros à l'issue d'une telle épreuve".

1) Établir la loi de probabilité de

$X$ .

2) Calculer l'espérance mathématique de

$X$ et déterminer

$n$ pour que le jeu soit le plus équitable possible.

3) Calculer l'écart-type de

$X$ lorsque

$n$ vaut 5.

Exercice 13

Une pisciculture dispose de deux bassins

$B_{1}$ et

$B_{2}$ qui contiennent, chacun, des turbots et des soles.

$B_{1}$ contient 10 poissons et

$B_{2}$ contient 12 poissons.

Le nombre total de soles est de 8.

On choisi au hasard un bassin et on extrait un poisson au hasard.

Pour chaque affirmation suivante, dire si elle est vraie ou fausse. Justifier.

1) (A) : Si la probabilité d'obtenir une sole provenant de

$B_{1}$ est

$\dfrac{1}{5}$ , alors

$B_{1}$ contient 2 soles.

2) (B) : Si la probabilité d'obtenir un turbot provenant de

$B_{2}$ est

$\dfrac{1}{3}$ , alors

$B_{1}$ contient 8 turbots.

3) (C) : Si la probabilité d'obtenir une sole sachant qu'elle provient de

$B_{2}$ est

$\dfrac{1}{3}$ , alors

$B_{2}$ contient 4 soles.

4) (D) : La probabilité d'obtenir un turbot est

$\dfrac{7}{11}$ .

5) (A) : Si

$B_{1}$ contient 4 soles, alors la probabilité d'obtenir une sole est

$\dfrac{11}{30}$ .

Exercice 14

On réalise une enquête auprès de 10000 personnes. Parmi elles,

$40\%$ sont fumeurs,

$4\%$ souffrent de bronchites, et

$75\%$ des personnes atteintes de bronchites sont des fumeurs.

1) Compléter le tableau suivant :

$\begin{array}{|c|c|c|c|}\hline&\text{Personnes atteintes}&\text{Personnes non atteintes}&\text{Totaux} \\ &\text{de bronchites}&\text{de bronchites}& \\ \hline\text{Fumeurs} & & & \\ \hline\text{Non fumeurs} & & & \\ \hline\text{Totaux} & & & 10000 \\ \hline\end{array}$

2) On choisit au hasard une de ces 10000 personnes.

a) Déterminer la probabilité de chacun des événements suivants :

$A$ : "la personne choisie est un fumeur" ;

$B$ : "la personne choisie est atteinte de bronchites" ;

$C$ : "la personne choisie est un fumeur non atteint de bronchites".

b) Exprimer littéralement les événements

$A\cap B$ et

$A\cup B$ , puis donner leurs probabilités.

c) Déterminer la probabilité que la personne choisie parmi les fumeurs soit non atteinte de bronchites.

Exercice 15

Un même individu peut être atteint de surdité unilatéral (portant sur une seule oreille) ou bilatérale (portant sur les deux oreilles).

On admet que, dans une population donnée, les deux événements :

$D$ : "être atteint de surdité à l'oreille droite" ;

$G$ : "être atteint de surdité à l'oreille gauche",

sont indépendants et tous deux de probabilité 0.05, ce que l'on note

$p(D)=p(G)=0.05.$

On considère les événements suivants :

$B$ : "être atteint de surdité bilatérale" ;

$U$ : "être atteint de surdité unilatérale" ;

$S$ : "être atteint de surdité (sur une oreille au moins" ;

N.B : on donnera les valeurs numériques des probabilités sous forme décimal approchées à

$10^{-4}$ près.

1) Exprimer les événements

$B$ et

$S$ à l'aide de

$G$ et de

$D$ , puis calculer les probabilités

$p(B)$ de

$B$ et

$p(S)$ de

$S.$

En déduire la probabilité

$p(U)$ de

$U$ .

2) Sachant qu'un sujet pris au hasard dans la population considérée est atteint de surdité, quelle est la probabilité :

a) Pour qu'il soit atteint de surdité à droite ?

b) Pour qu'il soit atteint de surdité bilatérale ?

$S$ étant réalisé, les deux événements sont-ils indépendants ?

3) On considère un échantillon de 10 personnes prises au hasard dans la population considérée, qui est suffisamment grande pour que les choix puissent être assimilés à deux choix successifs indépendants :

a) Quelle est la probabilité pour qu'il y ait exactement

$k$ personnes atteintes de surdité dans l'échantillon ?

b) Calculer la probabilité pour qu'il n'y ait aucun sujet atteint de surdité dans l'échantillon.

Exercice 16

Une urne contient 5 boules noires et 5 boules blanches, indiscernables au toucher. On en prélève

$n$ successivement et avec remise,

$n$ étant un entier naturel supérieur ou égal à 2. On considère les événements suivants :

$A$ : "on obtient des boules des deux couleurs".

$B$ : "on obtient au plus une blanche".

1) a) Calculer la probabilité de l'événement : "toutes les boules tirées sont de même couleur".

b) Calculer la probabilité de l'événement : "on obtient exactement une boule blanche".

c) En déduire que les probabilités

$p(A\cap B)\;,\ p(A)\;,\ p(B)$ sont :

$p(A\cap B)=\dfrac{n}{2^{n}}\;,\quad p(A)=1-\dfrac{1}{2^{n-1}}\;,\quad p(B)=\dfrac{n+1}{2^{n}}$

2) Montrer que

$p(A\cap B)=p(A)\cdot p(B)$ si, et seulement si,

$2^{n-1}=n+1.$

3) Soit

$(u_{n})$ la suite définie pour tout

$n\in\mathbb{N}\;;\ n\geq 2$ par :

$u_{n}=2^{n-1}-(n+1).$

a) Calculer

$u_{2}\;,\ u_{3}\;,\ u_{4}$ .

b) Démontrer que la suite

$(u_{n})$ est strictement croissante.

4) En déduire la valeur de l'entier

$n$ tel que les événements

$A$ et

$B$ soient indépendants.

Exercice 17

Une urne contient 2 boules blanches et 4 boules noires, indiscernables au toucher.

1) On effectue quatre tirages successifs d'une boule sans remise.

a) Calculer la probabilité de tirer dans l'ordre une boule noire, une boule noire, une boule noire et une boule blanche.

b) Calculer la probabilité de tirer une seule boule blanche au cours de ces quatre tirages.

2) On effectue maintenant quatre tirages successifs d'une boule avec remise.

Répondre aux mêmes questions qu'à la question 1).

3) Soit

$n\in\mathbb{N}\;;\ n>0$ , on effectue

$n$ tirages successifs avec remise.

On appelle

$P_{n}$ la probabilité d'obtenir au cours de ces

$n$ tirages une boule blanche uniquement au dernier tirage.

a) Calculer

$P_{1}\;,\ P_{2}\;,\ P_{3}$ et

$P_{n}$ .

b) Soit

$S_{n}=P_{1}+P_{2}+P_{3}+\ldots+P_{n}\quad(n>1).$

Exprimer

$S_{n}$ en fonction de

$n$ et déterminer la limite de

$S_{n}$

Exercice 18

Dans cet exercice,

$A$ et

$B$ étant deux événements,

$p(A)$ désigne la probabilité de

$A$ :

$p_{A}(B)$ la probabilité de

$B$ sachant que

$A$ est réalisé.

1) Le nombre de clients se présentant en cinq minutes dans une station-service est une variable aléatoire

$X$ dont on donne la loi de probabilité :

$p_{i}=p(\{X=i\})$

$\begin{array}{|c|c|c|c|}\hline i & 0 & 1 & 2 \\ \hline p_{i} & 0.1 & 0.5 & 0.4 \\ \hline\end{array}$

Calculer l'espérance mathématique de

$X$ .

2) Dans cette station-service, la probabilité qu'un client achète de l'essence est 0.7 ; celle qu'il achète du gazole est 0.3. Son choix est indépendant de celui des autres clients. On considère les événements suivants :

$C_{1}$ : "en cinq minutes, un seul client se présente" ;

$C_{2}$ : "en cinq minutes, deux clients se présentent" ;

$E$ : "en cinq minutes, un seul client achète de l'essence" ;

a) Calculer

$p(C_{1}\cap E)$ .

b) Montrer que

$p_{C_{1}}(E)=0.42$ et calculer

$p(C_{2}\cap E).$

c) En déduire la probabilité qu'en cinq minutes un seul client achète de l'essence.

3) Soit

$Y$ la variable aléatoire égale au nombre de clients achetant de l'essence en cinq minutes ; déterminer la loi de probabilité de

$Y.$

4) Les variables aléatoires

$X$ et

$Y$ sont-elles indépendantes ?

Exercice 19

On dispose d'un dé cubique dont les faces sont numérotées de 1 à 6. On désigne par

$p_{k}$ , la probabilité d'obtenir, lors d'un lancer numéroté

$k\;;\ (k\text{ est un entier et }1\leq k\leq 6).$

Ce dé a été pipé de telle sorte que :

$-\$ les six faces ne sont pas équiprobables ;

$-\$ les nombres

$p_{1}\;,\ p_{2}\;,\ p_{3}\;,\ p_{4}\;,\ p_{5}\;,\ p_{6}$ dans cet ordre, sont six termes consécutifs d'une suite géométrique.

1) Démontrer que :

$p_{k}=\dfrac{k}{21}$ pour tout entier

$k$ tel que

$1\leq k\leq 6.$

2) On lance ce dé une fois et on considère les événements suivants :

$A$ : "le nombre obtenu est pair".

$B$ : "le nombre obtenu est supérieur ou égal à 3".

$C$ : "le nombre obtenu est 3 ou 4".

a) Calculer la probabilité de chacun de ces événements.

b) Calculer la probabilité que le nombre obtenu soit supérieur ou égal à 3, sachant qu'il est pair.

c) Les événements

$A$ et

$B$ sont-ils indépendants ? Les événements

$A$ et

$C$ sont-ils indépendants ?

3) On utilise ce dé pour un jeu.

On dispose :

$-\$ d'une urne

$U_{1}$ contenant une boule blanche et trois boules noires ;

$-\$ d'une urne

$U_{2}$ contenant deux boules blanches et une boule noire ;

le joueur lance le dé :

$-\$ s'il obtient un nombre pair, il extrait au hasard une boule de l'urne

$U_{1}$ ;

$-\$ s'il obtient un nombre impair, il extrait au hasard une boule de l'urne

$U_{2}$ .

On suppose que les tirages sont équiprobables et le joueur est déclaré gagnant lorsqu'il tire une boule blanche, on note

$G$ cet événement.

a) Déterminer la probabilité de l'événement

$G\cap A$ puis la probabilité de l'événement

$G.$

b) Le joueur est gagnant. Déterminer la probabilité qu'il ait obtenu un nombre pair lors du lancer du dé.

Exercice 20

La durée de vie

$X$ d'un module électronique utilisé sur des moteurs suit la loi exponentielle, de paramètre

$\lambda=5\times 10^{-9}$ , pour un temps exprimé en secondes, que ce module fonctionne ou non.

1) Déterminer la probabilité pour qu'un tel module tombe en panne pendant la première année qui suit sa fabrication.

2) Lorsqu'un module est mis en place sur un moteur, on vérifie qu'il fonctionne. Montrer que la date de fabrication du module n'intervient pas sur sa durée de vie future.

3) Cinq modules sont montés sur chaque moteur et ils sont totalement indépendants les uns des autres. Le moteur ne peut plus fonctionner dès qu'un des modules au moins est en panne.

Quelle est la probabilité pour qu'un moteur tombe en panne la première année à cause des modules ?

Commentaires

Anonyme (non vérifié)

lun, 04/23/2018 - 21:09

Permalien

Pdf

répondre

Anonyme (non vérifié)

lun, 04/23/2018 - 21:11

Permalien

enregistrer les fiches d'exercice

pdf

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Exercices d'entraînement types du Bac : Dénombrement - Probabilités

Formulaire de recherche

I. Calcul avec des factorielles ou des (np)\dbinom{n}{p}

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

II. Dénombrement

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

Exercice 8

Exercice 9

Exercice 10

Exercice 11

Exercice 12

Exercice 13

III. Probabilités

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

Exercice 8

Exercice 9

Exercice 10

Exercice 11

Exercice 12

Exercice 13

Exercice 14

Exercice 15

Exercice 16

Exercice 17

Exercice 18

Exercice 19

Exercice 20

Commentaires

Pdf

enregistrer les fiches d'exercice

Ajouter un commentaire

Plain text

I. Calcul avec des factorielles ou des $\dbinom{n}{p}$