Exercices : Le Losange - 5e
Classe:
Cinquième
Exercice 1
A l'aide des instruments de géométrie, identifie les losanges parmi les figures ci-dessous en écrivant leur numéro.
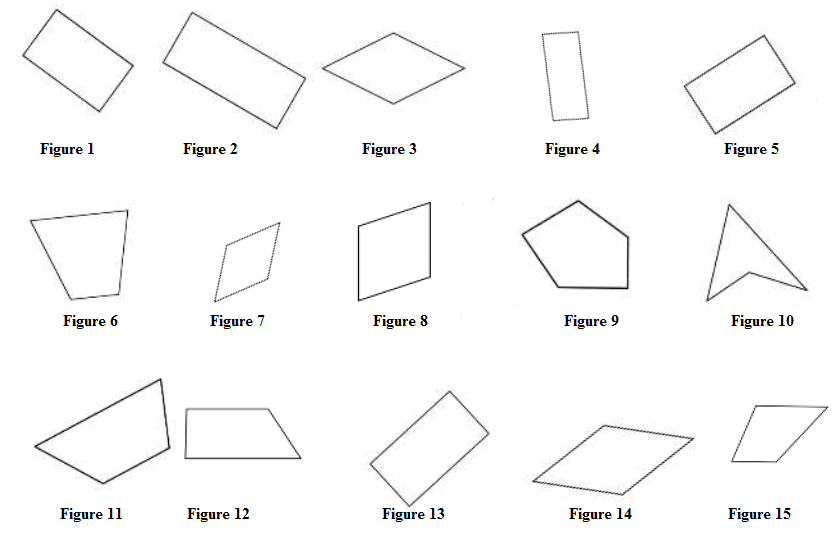
Exercice 2
1) Trace deux cercles $(\mathcal{C}_{1})\ $ et $\ (\mathcal{C}_{2})$ concentriques de centre $O.$
2) le segment $[AB]$ est un diamètre de $(\mathcal{C}_{1})\ $ et $\ [CD]$ est un diamètre $(\mathcal{C}_{2}).$ Les droites $(AB)\ $ et $\ (CD)$ sont perpendiculaires.
3) Quelle est la nature du quadrilatère $ACBD\ ?$ Justifier réponse.
Exercice 3
1) Citer deux parmi les propriétés du losange.
2) Comment reconnaître un losange? Donner deux exemples.
Exercice 4
1) Trace un segment $[MN]$ de $4\;cm$ et construire son milieu $J.$
2) Construire la droite $(d)$ médiatrice de $[MN].$
3) Marque sur cette médiatrice deux points distincts $A\ $ et $\ B$ tels que : $JA=JB.$
4) Quelle est la nature du quadrilatère $ACBD\ ?$ Justifier réponse.
Exercice 5
Reproduis le losange ci-dessous et trace ses diagonales. Code la figure obtenue.
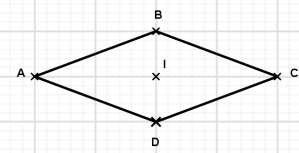
Exercice 6
1) Recopie et complète chacune des phrases ci-dessous par l'un des mots suivants : deux, quatre.
a) Si un quadrilatère a $\ldots\ldots$ côtés égaux alors c'est un losange.
b) Si un parallélogramme a $\ldots\ldots$ côtés consécutifs égaux alors c'est un losange.
2) Recopie et complète chacune des phrases ci-dessous par l’un des mots suivants : parallélogramme, quadrilatère.
a) Si un $\ldots\ldots\ldots\ldots$ a ses diagonales perpendiculaires alors c'est un losange.
b) Si un $\ldots\ldots\ldots\ldots$ a ses diagonales perpendiculaires et de même milieu alors c'est un losange.
c) Si un $\ldots\ldots\ldots\ldots$ a une diagonale qui est en même temps bissectrice alors c'est un losange.
Exercice 7
1) Construis un losange $EFGH$ avec $EF=3\;cm\ $ et $\ EG=5\;cm.$
2) Construis un losange $HOTE$ avec $OE=4\;cm\ $ et $\ HT=3\;cm.$
3) Construis un losange $ANGE$ de périmètre $20\;cm$ avec $AG=9\;cm.$
Exercice 8
$ABCD$ est un losange. La parallèle à $(BD)$ passant par $A$ coupe $(BC)$ en $E.$
1) Justifie que les droites $(AE)\ $ et $\ (AC)$ sont perpendiculaires.
2) Justifie que les points $E\;,\ B\ $ et $\ C$ sont alignés et que $B$ est le milieu du segment $[EC].$
Exercice 9
Soit un segment $[AB].$
1) Construis la médiatrice $(\Delta)$ de $[AB]$, elle coupe $(AB)$ en $O$ puis marque un point $I$ sur $(\Delta).$
2) Quelle est la nature du triangle $AIB\ ?$ Que représente $(\Delta)$ pour ce triangle ?
3) Place le point $I'$ symétrique de $I$ par rapport à $O.$
4) Donne la nature du triangle $AI'B.$ Déduis-en la nature du quadrilatère $AIBI'.$
Exercice 10
Trace un losange $ABCD$ tel que les diagonales $[AC]\ $ et $\ [BD]$ mesurent respectivement $6\;cm\ $ et $\ 4\;cm.$
Exercice 11
Trace le losange $ABCD$ tel que $DA=2.4\;cm\ $ et $\ \widehat{DAB}=30^{\circ}.$
Exercice 12
Reproduis la figure ci-dessous et place le point $C$ de la droite $(d)$ et le point $D$ tels que $ABCD$ soit un losange.
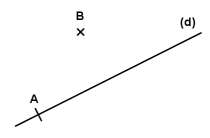
Exercice 13
1) Construis un triangle $OTE$ isocèle en $O$ tel que $\widehat{O}=75^{\circ}.$
2) a) Construis le parallélogramme $TOES$ de centre $I.$
b) Quelle est la nature exacte du quadrilatère $TOES\ ?$ Justifie.
3) a) Trace la droite $(\Delta)$ parallèle à $(OS)$ passant par $E.$
b) Trace la droite $(D)$ passant par $O$ et parallèle à $(TE).$
4) Les droites $(\Delta)\ $ et $\ (D)$ se coupent en $F.$ Justifie que le quadrilatère $FOIE$ est un rectangle.
Auteur:
Diny Faye & adem

Commentaires
Maodo Niang (non vérifié)
dim, 03/23/2025 - 12:54
Permalien
Demande d'une correction pour les exercices de losange
Ajouter un commentaire