Exercices : Vecteurs 3e
Classe:
Troisième
Exercice 1
$L,\ O,\ U$ sont trois points non alignés du plan. $S$ est le milieu du segment $[OU].$
1) Construis le point $I$ tel que : $\overrightarrow{LI}=\overrightarrow{LO}+\overrightarrow{LU}$
2) Démontre que : $\overrightarrow{LO}+\overrightarrow{LU}=2\overrightarrow{LS}$
Exercice 2
Un parallélogramme $ABCD$ a pour centre $O$. Soit $M$ un point quelconque du plan.
1) Construire un point $N$ tel que $\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MN}$
2) Montrer que $\overrightarrow{MN}=2\overrightarrow{MO}$
3) Montrer que $\overrightarrow{MB}+\overrightarrow{MD}=\overrightarrow{MN}$
4) En déduire que $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=4\overrightarrow{MO}$
Exercice 3
Soit un parallélogramme $ABCD.$ Place un point $M$ quelconque sur la diagonale $[BD].$
1) Construis les points $E$ et $F$ vérifiant : $$\overrightarrow{AM}+\overrightarrow{AD}=\overrightarrow{AE}\quad\text{et}\quad\overrightarrow{AM}+\overrightarrow{AB}=\overrightarrow{AF}$$
2) Cite deux vecteurs égaux à $\overrightarrow{AD}$. En déduire que $MBCE$ est un parallélogramme.
3) Cite deux vecteurs égaux à $\overrightarrow{AB}$. Que peut-on en déduire pour le quadrilatère $MDCF\; ?$
4) Démontre, en utilisant les questions précédentes, que les points $E,\ C$ et $F$ sont alignés.
Exercice 4
1) Construire le triangle $ABC$ tel que $AB=5\;cm\;;\ AC=4\;cm$ et $BC=3\;cm.$
2) On pose $\vec{u}=\overrightarrow{AB}\;;\ \vec{v}=\overrightarrow{AC}$. Construire $\vec{u}+\vec{v}$
3) Placer le point $E$ tel que $\overrightarrow{AE}=\vec{u}+\vec{v}$ et diviser le segment $[AE]$ en trois parties égales.
4) On pose $\vec{w}=\overrightarrow{BC}$. Construire $\vec{u}+\vec{v}+\vec{w}$
5) Soit $G$ un point du plan tel que $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}.$
Démontrer que $\overrightarrow{AG}=\dfrac{\overrightarrow{AB}+\overrightarrow{AC}}{3}$
Exercice 5
1) a) Tracer un rectangle $ABCD$ de centre $I.$
Construire le point $K$ tel que $\overrightarrow{IK}=\overrightarrow{IA}+\overrightarrow{IB}$
b) Montrer que le quadrilatère $AKBI$ est un losange.
2) a) Construire le point $P$, symétrique de $I$ par rapport à $B$, et le point $R$, symétrique de $K$ par rapport à $B.$
b) Prouver que les points $I,\ K,\ P$ et $R$ sont sur un même cercle. Indiquer le centre et le rayon de ce cercle. Construire ce cercle sur la figure.
c) En déduire la nature du quadrilatère $IKPR$.
Exercice 6
1) Construire un triangle isocèle $ABC$ de sommet $A$ tel que : $AB=4.5\;cm$ et $BC=5.4\;cm$
Placer le point $H$, pied de la hauteur issue de $A$, et le point $M$, milieu de $[AB].$
2) Justifier que $H$ est le milieu de $[BC].$
3) Calculer la longueur du segment $[MH].$
4) Construire le point $D$, symétrique du point $M$ par rapport au point $H$. Quelle est la nature du quadrilatère $BMCD\; ?$ Justifier la réponse.
5) Démontrer que : $\overrightarrow{AM}+\overrightarrow{BD}=\overrightarrow{MD}$
Exercice 7
Soit $I$ le milieu d'un segment $[AB]$ et $M$ un point n'appartenant pas à $(AB).$
1)Construire les points $C$ et $D$ tels que $$\overrightarrow{IC}=\overrightarrow{IA}+\overrightarrow{IM}\quad\text{et}\quad\overrightarrow{ID}=\overrightarrow{IB}+\overrightarrow{IM}$$
2) Démontrer que $M$ est le milieu de $[CD]$
3) Démontrer que $\overrightarrow{IC}=\overrightarrow{BM}$
4) Soit $E$ le symétrique de $I$ par rapport à $M$. Démontrer que $\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{IE}$
Exercice 8
$A,\ B$ et $C$ sont trois points non alignés.
1) Construis le point $L$ tel que $\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{BL}$
2) La parallèle à $(AC)$ passant par $L$ coupe $(BA)$ en $M$ et $(BC)$ en $N$
Démontre que $\overrightarrow{AC}=\overrightarrow{ML}=\overrightarrow{LN}$
Exercice 9
Soit $ABC$ un triangle ; $\vec{u}$ et $\vec{v}$ deux vecteurs tels que $\vec{u}=\overrightarrow{AB}$ et $\vec{v}=\overrightarrow{AC}$
Soit $I$ le milieu de $[BC]$
1) Démontrer que $\vec{u}+\vec{v}=2\overrightarrow{AI}$
2) Soit $D$ le point tel que $\vec{u}+\vec{v}=\overrightarrow{AD}$ ; la parallèle à $(BC)$ passant par $D$ coupe $(AB)$ en $E$ et $(AC)$ en $F.$
Démontrer que $\overrightarrow{AE}=2\overrightarrow{AB}$ et $\overrightarrow{AF}=2\overrightarrow{AC}$
3) Déterminer le réel $k$ tel que $\overrightarrow{EF}=k\overrightarrow{CB}$
4) Démontrer que $\overrightarrow{AE}+\overrightarrow{AF}=4\overrightarrow{AI}$
Exercice 10
1) Tracer un triangle $BDS$ et marquer le milieu $I$ du segment $[SD]$
2) Construire le point $H$ symétrique du point $B$ par rapport à $I.$
3) Démontrer que $\overrightarrow{HD}=\overrightarrow{SB}$
4) Construire le point $R$, image du point $D$ par la translation de vecteur $\overrightarrow{SB}$
5) Démontrer que le point $D$ est le milieu du segment $[HR].$
Exercice 11
$A,\ B$ et $C$ sont trois points du plan. $M'$ est l'image de $M$ par la translation de vecteur $\overrightarrow{AB}$ et $M''$ est l'image de $M'$ par la translation de vecteur $\overrightarrow{BC}.$
1) Démontrer que $\overrightarrow{MM'}=\overrightarrow{AB}$ et $\overrightarrow{M'M''}=\overrightarrow{BC}$
2) Démontrer que $\overrightarrow{AM}=\overrightarrow{CM''}$
3) Démontrer que $\overrightarrow{MM''}=\overrightarrow{AC}$
Exercice 12
1) Construire un triangle isocèle $ABC$ de sommet $A$ tel que $AB=4.5\;cm$ et $BC=5.4\;cm.$
Placer le point $H$, pied de la hauteur issue de $A$, et le point $M$, milieu de $[AB].$
2) Justifier que $H$ est milieu de $[BC]$.
3) Calculer la longueur du segment $[HA]$.
4) Construire le point $D$, symétrique du point $M$ par rapport au point $H.$
Quelle est la nature du quadrilatère $BMCD$ ? Justifier la réponse.
5) Démontrer que : $\overrightarrow{AM}+\overrightarrow{BD}=\overrightarrow{MD}$
Exercice 13
Dessiner un triangle quelconque $ABC$, placer un point $M$ sur $[AB]$, et un point $N$ sur $[AC]$ de façon à ce que les droites $(MN)$ et $(BC)$ soient parallèles.
1) Soit $K$ le point de $(BC)$ tel que $(NK)$ soit parallèle à $(AB)$. Recopier et compléter : $$\overrightarrow{BK}+\overrightarrow{BM}=\ldots\qquad\overrightarrow{MN}+\overrightarrow{KC}=\ldots$$
2) Quelle est l'image de $B$ par la translation de vecteur $\overrightarrow{MN}+\overrightarrow{KM}\; ?$ Justifier.
Exercice 14
Simplifier les expressions suivantes en précisant les propriétés de l'addition vectorielle utilisées.
$\vec{E}_{1}=\overrightarrow{AB}-\overrightarrow{EG}+\overrightarrow{BC}+\overrightarrow{FG}-\overrightarrow{FE}+\vec{0}-\overrightarrow{AC}$
$\vec{E}_{2}=5\sqrt{3}\overrightarrow{AB}-2\sqrt{2}\overrightarrow{DC}-2\sqrt{3}\overrightarrow{BA}-5\sqrt{2}\overrightarrow{DC}$
Exercice 15
Répondre par vrai on faux en justifiant la réponse
1) Si $ABCD$ est un parallélogramme alors : $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{DB}.$
2) Si $E\;,\ D$ et $F$ sont trois points distincts du plan d'après la relation de Chasles on a : $$\overrightarrow{DE}+\overrightarrow{DF}=\overrightarrow{EF}$$
3) Le vecteur $\overrightarrow{AB}-\overrightarrow{AC}-\overrightarrow{CB}$ est un vecteur nul.
4) Si $ABCD$ est un parallélogramme de centre $O$ alors : $\overrightarrow{AB}+\overrightarrow{AD}=2\overrightarrow{OC}$
5) Si $\overrightarrow{AE}=\overrightarrow{RS}$ alors les segments $[AS]$ et $[RE]$ ont le même milieu.
Exercice 16
Démontrer chacune des égalités suivantes.
1) $\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{BC}$
2) $\overrightarrow{MA}+2\overrightarrow{MB}-3\overrightarrow{MC}=2\overrightarrow{AB}-3\overrightarrow{AC}$
Exercice 17
On donne les égalités vectorielles suivantes : $\overrightarrow{AB}=2\overrightarrow{CD}$ et $\overrightarrow{CD}=4\overrightarrow{EF}.$
1) Exprimer $\overrightarrow{AB}$ en fonction de $\overrightarrow{EF}.$
2) Exprimer $\overrightarrow{EF}$ en fonction de $\overrightarrow{AB}$
3) Conclure.
Exercice 18
Soit $ABC$ un triangle tel que : $AB=2\;cm\;;\ AC=3\;cm$ et $BC=4\;cm.$
1) Construire le point $M$ tel que : $\overrightarrow{AM}=3\overrightarrow{AB}+2\overrightarrow{CA}$
2) Construire le point $M$ tel que : $\overrightarrow{AN}=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{CA}$
3) Montrer que : $\overrightarrow{AM}=3\overrightarrow{AN}$
En déduire que les points $A\;,\ M$ et $N$ sont alignés.
Exercice 19
$ABC$ est un triangle et $G$ le point du plan tel que : $\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}=\vec{0}.$
1) Montrer que le point $G$ est unique.
2) Construire le point $G.$
3) Soit $I$ milieu de $[AB]$; montrer que : $\overrightarrow{IG}=\dfrac{1}{2}\overrightarrow{GC}.$
Exercice 20
1) On considère un triangle $ABC$, tel que : $AB=5\;cm\;;\ BC=6\;cm$ et $AC=7\;cm.$ Soit $I$ milieu de $[AB].$
Construire le point $G$ centre gravité du triangle $ABC.$
2) Sachant que : $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}.$ Démontrer que pour tout point $M$ du plan, on a : $$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}$$
Exercice 21
$ABC$ est un triangle quelconque, les points $D$ et $F$ sont tels que :
$\overrightarrow{AD}=\overrightarrow{BC}-2\overrightarrow{BA}$ et $\overrightarrow{CF}=\overrightarrow{AB}-2\overrightarrow{AC}$
1) Démontrer que :
a) $\overrightarrow{AD}=\overrightarrow{AC}+\overrightarrow{AB}$
b) $\overrightarrow{CF}=\overrightarrow{CB}+\overrightarrow{CA}$
2) Construire les points $D$ et $F.$
3) En déduire que le point $B$ est le milieu du segment $[DF].$
Exercice 22
1) On considère un segment $[AB]$ de milieu $I$, démontrer que pour tout point $M$,
$$\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}$$
2) $ABC$ est un triangle, on suppose qu'il existe un point $H$ tel que
$\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}=\vec{0}$, en utilisant $I$ milieu de $[AB]$, démontrer que $H$ est un point de $[IC].$
Exercice 23
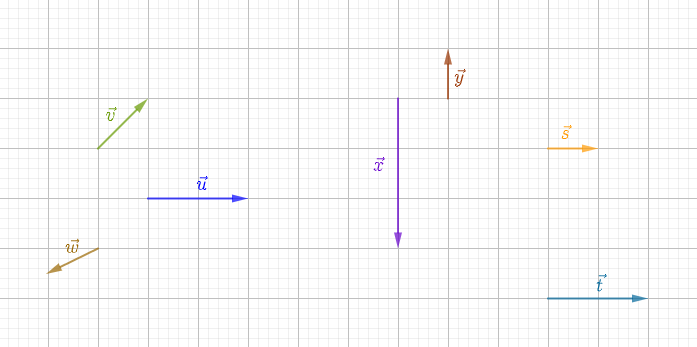
Reproduis la figure ci-dessous en utilisant le quadrillage du cahier puis construis les vecteurs
$\overrightarrow{u}+\overrightarrow{v}$ ;
$\overrightarrow{x}+\overrightarrow{y}$ ;
$\overrightarrow{u}+\overrightarrow{w}$ ;
$\overrightarrow{s}+\overrightarrow{t}$

Exercice 24
a) Construis un triangle $ABC$ tel que $AB=4\;cm$, $AC=3.5\;cm$ et $BC=3\;cm.$
b) Construis les vecteurs :
$\overrightarrow{AB}+\overrightarrow{AC}$ ;
$\overrightarrow{BA}+\overrightarrow{BC}$ et $\overrightarrow{CA}+\overrightarrow{CB}.$
c) Marque le point $E$ milieu de $[AB]$ puis construis le vecteur $\overrightarrow{AE}+\overrightarrow{CB}$
Exercice 25
Soit $ABC$ un triangle.
1) a) Construis les points $E$ et $F$ tels que :
$\overrightarrow{CE}=\dfrac{-1}{3}\overrightarrow{CA}$ et $\overrightarrow{CF}=\dfrac{-1}{3}\overrightarrow{CB}.$
b) Démontre que les droites $(EF)$ et $(AB)$ sont parallèles.
2) a) Construis les points $O$ et $N$ tels que :
$\overrightarrow{EO}=\dfrac{2}{5}\overrightarrow{EF}$ et $\overrightarrow{AN}=\dfrac{2}{5}\overrightarrow{AB}$
b) Démontre que les points $C$, $O$ et $N$ sont alignés.
Exercice 26
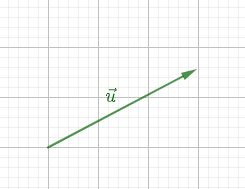
Reproduis la figure ci-dessous en utilisant le quadrillage du cahier puis construis les vecteurs :
$2\overrightarrow{u}\;;\ \overrightarrow{-u}$ ;
$\dfrac{3}{2}\overrightarrow{u}\;;\ -\dfrac{2}{3}\overrightarrow{u}.$

Exercice de Synthèse
a) Tracer un parallélogramme $ABCD$ de centre $O.$
On note $I$ le milieu de $[AB].$
b) Simplifier les sommes vectorielles suivantes en un seul vecteur
$\overrightarrow{OA}+\overrightarrow{OC}=\ldots$
$\overrightarrow{AB}+\overrightarrow{AD}=\ldots$
$\overrightarrow{CD}+\overrightarrow{CB}=\ldots$
$\overrightarrow{OI}+\overrightarrow{OI}+\overrightarrow{AD}=\ldots$
I. $ABCD$ est un parallélogramme alors :
a) $\overrightarrow{AB}=\overrightarrow{DC}$
b) $\overrightarrow{AD}=\overrightarrow{AB}$
c) $\overrightarrow{CB}=\overrightarrow{DA}$
II. Pour trois points quelconques du plan $M$, $N$ et $P$ :
$\overrightarrow{MN}+\overrightarrow{NP}$ est égal à :
a) $\overrightarrow{NP}$ b) $\overrightarrow{PM}$ c) $\overrightarrow{MP}$

Commentaires
Anonyme (non vérifié)
mer, 05/01/2019 - 00:31
Permalien
Vous êtes les meilleurs
Anonyme (non vérifié)
mar, 07/02/2019 - 16:37
Permalien
Je vous remercie de votre
Anonyme (non vérifié)
mer, 01/08/2020 - 00:44
Permalien
Comment faire pour obtenir le
Anonyme (non vérifié)
mer, 01/08/2020 - 00:44
Permalien
Comment faire pour obtenir le
ibrahima BA (non vérifié)
lun, 08/31/2020 - 21:55
Permalien
c'est super
Anonyme (non vérifié)
mar, 02/23/2021 - 13:08
Permalien
mmlljml
Anonyme (non vérifié)
jeu, 07/01/2021 - 17:50
Permalien
Merci pour votre aide
Anonyme (non vérifié)
lun, 07/05/2021 - 16:01
Permalien
Télécharger
Mary (non vérifié)
mar, 08/03/2021 - 12:37
Permalien
Télécharger en pdf
ALHASSANE DABO (non vérifié)
mar, 09/06/2022 - 12:22
Permalien
Bien
Anonyme (non vérifié)
sam, 01/18/2025 - 11:15
Permalien
bon choix des exercices avec
Ajouter un commentaire