Fonction Ln - TL
Classe:
Terminale
1. Définition
Nous admettrons qu'il existe une seule fonction $F$ ayant les trois propriétés suivantes :
$\bullet\ $Elle n'est définie que pour $x>0$, soit sur $]0\ ;\ +\infty[$ ;
$\bullet\ $Elle s'annule pour $x=1$, soit $F(1)=0.$
$\bullet\ $Elle admet pour fonction dérivée $F'$ telle que $F'(x)=\dfrac{1}{x}\forall\,x>0.$
Cette fonction est appelée fonction logarithme népérien $($notée en abrégé $\ln).$
2. Propriétés fondamentales
1. $\forall\;a>0$, $\forall\;b>0$, $\ln ab=\ln a+\ln b.$
2. $\forall a\;>0$, $\forall\;b>0$, $\ln\dfrac{a}{b}=\ln a-\ln b$
3. $\forall\;n\in\mathbb{Z}$, $\forall\;a>0$, $\ln a^{n}=n\ln a$
cas particulier :
$\forall\;a>0$, $\ln\dfrac{1}{a}=-\ln a.$
4. $\forall\;a>0$, $=\ln\sqrt{a}=\dfrac{1}{2}\ln a.$
$\bullet\ $Limites importantes
$\lim\limits_{x\;\longrightarrow\;0^{+}}\ln x=-\infty$
$\lim\limits_{x\;\longrightarrow\;+\infty}\ln x=+\infty$
$\lim\limits_{x\;\longrightarrow\;0^{+}}x\ln x=0$
$\lim\limits_{x\;\longrightarrow\;+\infty}\dfrac{\ln x}{x}$
$\lim\limits_{x\;\longrightarrow\;0^{+}}\dfrac{\ln(1+x)}{x}=1.$
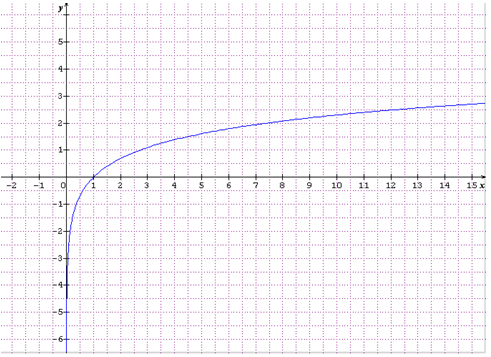
4. Représentation graphique
Par définition, la fonction $\ln$ est dérivable sur $\mathbb{R}^{+\ast}$ et on a :
$(\ln x)^{\prime}=\dfrac{1}{x}\forall\;x>0$
Tableau de variation
Tableau
Tableau de valeurs
$$\begin{array}{|l|c|c|c|c|c|c|} \hline x&0.1&0.3&0.5&1&2&3\\ \hline \ln x&-2.303&-1.204&-0.693&0&0.693&1.099\\ \hline \end{array}$$
$$\begin{array}{|l|c|c|c|c|c|c|} \hline x&4&5&6&7&8&9\\ \hline \ln x&1.386&1.609&1.792&1.946&2.079&2.197\\ \hline \end{array}$$
Exercice d'application :
Donner les équations des tangentes à $\mathfrak{C}$, courbe représentative de $\ln$ aux points d'abscisse respectives $1$ et $\mathrm{e}$
Propriété admise
La fonction la réalise une bijection de $]0\ ;\ +\infty[$ vers $\mathbb{R}.$
Cela signifie que pour tout réel $\lambda$ l'équation $f(x)=\lambda$ admet une solution et une seule.
En particulier, il existe un nombre et un seul, noté $\mathrm{e}$ tel que : $\ln\mathrm{e}=1.$
$\mathrm{e}\approx 2.7182818\ldots$
Une autre conséquence de cette propriété est qu'on a les équivalences suivantes :
1. $\forall a>0\;,\ \forall b>0\;,\quad\ln a=\ln b\Leftrightarrow\;a=b$
2. $\forall a>0\;,\ \forall b>0\;,\quad\ln a>\ln b\Leftrightarrow\;a>b$
3. $\forall a>0\;,\ \forall b>0\;,\quad\ln a<\ln b\Leftrightarrow\;a<b$
4. $(\ln x)<0\Leftrightarrow(0<x<1)$
5. $(\ln x)=0\Leftrightarrow(x=1)$
6. $(\ln x)>0\Leftrightarrow(x>1).$
7. $\forall\;m\in\mathbb{Z}\;,\ \ln x=m\Leftrightarrow\left(x=\mathrm{e}^{m}\right)\text{ car }\ln\mathrm{e}^{m}=m\ln\mathrm{e}=m$

Commentaires
Anonyme (non vérifié)
ven, 04/26/2024 - 12:43
Permalien
J’apprécie énormément
Ajouter un commentaire