Fonctions exponentielles - Fonctions puissances - Croissances comparées - T S
Classe:
Terminale
I Définition et propriétés
I.1 Définition
La fonction $f(x)=\ln x$ est continue et strictement croissante sur $]0\;;\ +\infty[$ donc, c'est une bijection de $]0\;;\ +\infty[$ vers $\mathbb{R}$ d'où, $f$ admet une bijection réciproque $f^{-1}$ qui est continue et strictement croissante de $\mathbb{R}$ vers $]0\;;\ +\infty[.$
$f^{-1}$ est appelée fonction exponentielle notée : $$exp(x)=\mathrm{e}^{x}$$
I.2 Propriétés
$\centerdot\ \ \ln x=y\ $ si, et seulement si, $\ \mathrm{e}^{y}=x$
$\centerdot\ \ \ln\mathrm{e}^{x}=x\;,\quad\mathrm{e}^{\ln x}=x$
$\centerdot\ \ a=b\ $ si, et seulement si, $\ \mathrm{e}^{a}=\mathrm{e}^{b}$
$\centerdot\ \ a\geq b\ $ si, et seulement si, $\ \mathrm{e}^{a}\geq\mathrm{e}^{b}$
$\centerdot\ \ \mathrm{e}^{a+b}=\mathrm{e}^{a}\times\mathrm{e}^{b}$
On a : $a=\ln x\ \Leftrightarrow\ x=\mathrm{e}^{a}\ $ et $\ b=\ln y\ \Leftrightarrow\ y=\mathrm{e}^{b}$ donc,
$\begin{array}{rcl}\mathrm{e}^{a+b}&=&\mathrm{e}^{\ln x+\ln y}\\&=&\mathrm{e}^{\ln xy}\\&=&xy\\&=&\mathrm{e}^{a}\times\mathrm{e}^{b}\end{array}$
D'où : $\mathrm{e}^{a+b}=\mathrm{e}^{a}\times\mathrm{e}^{b}$
$\centerdot\ \ \mathrm{e}^{-a}=\dfrac{1}{\mathrm{e}^{a}}$
En effet, on a : $a=\ln x\ \Leftrightarrow\ x=\mathrm{e}^{a}$
Donc,
$\begin{array}{rcl}\mathrm{e}^{-a}&=&\mathrm{e}^{-\ln x}\\&=&\mathrm{e}^{\ln\frac{1}{x}}\\ &=&\dfrac{1}{x}\ =\ \dfrac{1}{\mathrm{e}^{a}}\end{array}$
D'où, $\mathrm{e}^{-a}=\dfrac{1}{\mathrm{e}^{a}}$
$\centerdot\ \ \mathrm{e}^{a-b}=\dfrac{\mathrm{e}^{a}}{\mathrm{e}^{b}}$
$\centerdot\ \ \forall\;p\in\mathbb{Z}\;,\quad(\mathrm{e}^{a})^{p}=\mathrm{e}^{pa}$
$\centerdot\ \ \mathrm{e}^{0}=1$
$\centerdot\ \ (\mathrm{e}^{x})'=\mathrm{e}^{x}$
En effet, soit $f(x)=y=\ln x$ alors, $f^{-1}(y)=x=\mathrm{e}^{y}.$
Par suite,
$\begin{array}{rcl} (f^{-1})'(y)&=&(\mathrm{e}^{y})'\\ \\&=&\dfrac{1}{f'(x)}\\ \\&=&\dfrac{1}{\dfrac{1}{x}}\ =\ x\ =\ \mathrm{e}^{y}\end{array}$
D'où : $(\mathrm{e}^{x})'=\mathrm{e}^{x}$
$\centerdot\ \ (\mathrm{e}^{u})'=u'\times\mathrm{e}^{u}$ avec $u$, une fonction définie et dérivable sur un intervalle $I$ de $\mathbb{R}.$
Exercice d'application
Simplifier les écritures des nombres $A\ $ et $\ B$ suivants :
$A=\dfrac{\mathrm{e}^{5}\times\mathrm{e}^{-3}}{(\mathrm{e}^{3})^{2}}$
$B=\dfrac{\mathrm{e}^{x}\times\mathrm{e}^{2-y}}{\mathrm{e}^{-y+x}}+\mathrm{e}^{0}$
Résolution
$\begin{array}{rcl} A&=&\dfrac{\mathrm{e}^{5}\times\mathrm{e}^{-3}}{(\mathrm{e}^{3})^{2}}\\ \\&=&\dfrac{\mathrm{e}^{5-3}}{\mathrm{e}^{2\times 3}}\\ \\&=&\dfrac{\mathrm{e}^{2}}{\mathrm{e}^{6}}\\ \\&=&\mathrm{e}^{2-6}\ =\ \mathrm{e}^{-4}\\ \\&=&\dfrac{1}{\mathrm{e}^{4}}\end{array}$
D'où : $A=\left(\dfrac{1}{\mathrm{e}}\right)^{4}$
$\begin{array}{rcl} B&=&\dfrac{\mathrm{e}^{x}\times\mathrm{e}^{2-y}}{\mathrm{e}^{-y+x}}+\mathrm{e}^{0}\\ \\&=&\dfrac{\mathrm{e}^{2}\times\mathrm{e}^{x}\times\mathrm{e}^{-y}}{\mathrm{e}^{-y}\times\mathrm{e}^{x}}+1\\ \\&=&\mathrm{e}^{2}+1\end{array}$
D'où : $B=\mathrm{e}^{2}+1$
II Équations - Inéquations
Exemple
Résoudre dans $\mathbb{R}$
a) $\mathrm{e}^{3x}+\mathrm{e}^{2x}-10\mathrm{e}^{x}+8=0$
b) $2\mathrm{e}^{x}+\mathrm{e}^{-x}-2\leq 0$
Résolution
a) L'équation peut se mettre sous la forme $(\mathrm{e}^{x})^{3}+(\mathrm{e}^{x})^{2}-10\mathrm{e}^{x}+8=0.$
Posons $X=\mathrm{e}^{x}$
Donc, l'équation qui devient $X^{3}+X^{2}-10X+8=0$ admet comme solutions 1, -4 et 2.
Par suite, après retour sur le changement de variable on obtient :
$\mathrm{e}^{x}=1\ \Rightarrow\ x=\ln 1=0$
$\mathrm{e}^{x}=-4$ impossible
$\mathrm{e}^{x}=2\ \Rightarrow\ x=\ln 2$
D'où, $S=\{0\;;\ \ln 2\}$
b) On a :
$\begin{array}{rcl} 2\mathrm{e}^{2x}+\mathrm{e}^{-x}-2\leq 0&\Leftrightarrow&2\mathrm{e}^{x}+\dfrac{1}{\mathrm{e}^{x}}-2\leq 0\\ \\&\Leftrightarrow&\dfrac{2\mathrm{e}^{2x}-2\mathrm{e}^{x}+1}{\mathrm{e}^{x}}\leq 0\end{array}$
Or, $\mathrm{e}^{x}>0$ donc, le signe de $\dfrac{2\mathrm{e}^{2x}-2\mathrm{e}^{x}+1}{\mathrm{e}^{x}}$ dépend uniquement du signe de $2\mathrm{e}^{2x}-2\mathrm{e}^{x}+1.$
Posons $X=\mathrm{e}^{x}$ alors, $2\mathrm{e}^{2x}-2\mathrm{e}^{x}+1$ devient $2X^{2}-2X+1.$
$\Delta=4-8=-4<0$ donc, le trinôme $2X^{2}-2X+1$ est toujours positif.
Par suite, $2\mathrm{e}^{2x}-2\mathrm{e}^{x}+1>0\;,\ \forall\;x\in\mathbb{R}.$
Par conséquent, $2\mathrm{e}^{x}+\mathrm{e}^{-x}-2\leq 0$ est impossible.
D'où, $S=\emptyset$
III Courbe et compléments
Soit $g$ la fonction définie par $g(x)=\mathrm{e}^{x}$ de courbe représentative $C_{g}$ alors, $D_{g}=\mathbb{R}$ et $g'(x)=\mathrm{e}^{x}$
On sait que : $\mathrm{e}^{x}\geq x\;,\ \forall\;x\in\mathbb{R}$ et que $\lim\limits_{x\rightarrow +\infty}x=+\infty$ donc, d'après le théorème de comparaison on a : $\lim\limits_{x\rightarrow +\infty}g(x)=+\infty$
D'où : $\boxed{\lim_{x\rightarrow +\infty}\mathrm{e}^{x}=+\infty}$
Calculons alors $\lim\limits_{x\rightarrow +\infty}\dfrac{g(x)}{x}$
On a :
$\begin{array}{rcl}\lim\limits_{x\rightarrow +\infty}\dfrac{g(x)}{x}&=&\lim\limits_{x\rightarrow +\infty}\dfrac{\mathrm{e}^{x}}{x}\\ \\&=&\lim\limits_{x\rightarrow +\infty}\dfrac{\mathrm{e}^{x}}{\mathrm{e}^{\ln x}}\\ \\&=&\lim\limits_{x\rightarrow +\infty}\mathrm{e}^{x-\ln x}\\ \\&=&\lim\limits_{x\rightarrow +\infty}\mathrm{e}^{x(1-\frac{\ln x}{x})}\\ \\&=&+\infty\quad\text{car }\lim\limits_{x\rightarrow +\infty}\left(1-\dfrac{\ln x}{x}\right)=1\end{array}$
Donc, $\lim\limits_{x\rightarrow +\infty}\dfrac{g(x)}{x}=+\infty$
D'où : $\boxed{\lim_{x\rightarrow +\infty}\dfrac{\mathrm{e}^{x}}{x}=+\infty}$
Ainsi, $C_{g}$ admet une branche parabolique de direction $(y'Oy).$
$\begin{array}{rcl}\lim\limits_{x\rightarrow -\infty}g(x)&=&\lim\limits_{x\rightarrow -\infty}\mathrm{e}^{x}\\ \\&=&\lim\limits_{X\rightarrow +\infty}\mathrm{e}^{-X}\quad\text{avec } X=-x\\ \\&=&\lim\limits_{X\rightarrow +\infty}\dfrac{1}{\mathrm{e}^{X}}\\ \\&=&0\end{array}$
Donc, $\lim\limits_{x\rightarrow -\infty}g(x)=0$
D'où : $\boxed{\lim_{x\rightarrow -\infty}\mathrm{e}^{x}=0}$
Par conséquent, $C_{g}$ admet en $-\infty$, une asymptote horizontale d'équation $y=0$.
Par ailleurs, $g'(x)=\mathrm{e}^{x}>0$ donc, $g$ est strictement croissante.
Tableau de variation
$$\begin{array}{|c|lcr|}\hline x&-\infty&&+\infty\\ \hline g'(x)&&+&\\ \hline&&&+\infty\\ g&&\nearrow&\\&0&&\\ \hline\end{array}$$
Soit $T_{0}$ et $T_{1}$ les tangentes à $C_{g}$ respectivement aux points d'abscisses 0 et 1 alors on a :
$\begin{array}{rcl} T_{0}\ :\ y&=&g'(0)(x-0)+g(0)\\ \\&=&x+1\end{array}$
Donc, $\boxed{T_{0}\ :\ y=x+1}$
$\begin{array}{rcl} T_{1}\ :\ y&=&g'(1)(x-1)+g(1)\\ \\&=&\mathrm{e}(x-1)+\mathrm{e}\\ \\&=&\mathrm{e}x\end{array}$
D'où : $\boxed{T_{1}\ :\ y=\mathrm{e}x}$
Représentation graphique
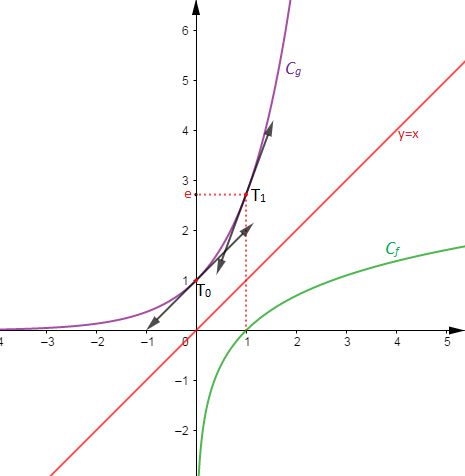
Remarque
Les fonctions $f(x)=\ln x\ $ et $\ g(x)=\mathrm{e}^{x}$ étant réciproques alors, leur courbe représentative $C_{f}\ $ et $\ C_{g}$ sont symétriques par rapport à la première bissectrice d'équation $y=x.$
Autres limites
La fonction $g(x)=\mathrm{e}^{x}$ est dérivable sur $\mathbb{R}$ donc dérivable en 0.
Par suite,
$\begin{array}{rcl}\lim\limits_{x\rightarrow 0}\dfrac{\mathrm{e}^{x}-1}{x}&=&\lim\limits_{x\rightarrow 0}\dfrac{g(x)-g(0)}{x-0}\\ \\&=&g'(0)\\ \\&=&1\end{array}$
D'où : $\boxed{\lim_{x\rightarrow 0}\dfrac{\mathrm{e}^{x}-1}{x}=1}$
$\begin{array}{rcl}\lim\limits_{x\rightarrow -\infty}x\mathrm{e}^{x}&=&\lim\limits_{X\rightarrow +\infty}-X\mathrm{e}^{-X}\quad\text{avec }X=-x\\ \\&=&\lim\limits_{X\rightarrow +\infty}-\dfrac{X}{\mathrm{e}^{X}}\\ \\&=&0\end{array}$
Ainsi, $\boxed{\lim_{x\rightarrow -\infty}x\mathrm{e}^{x}=0}$
$\begin{array}{rcl}\lim\limits_{x\rightarrow 0}x\mathrm{e}^{x}&=&\lim\limits_{x\rightarrow 0}\mathrm{e}^{\ln x}\mathrm{e}^{x}\\ \\&=&\lim\limits_{x\rightarrow 0}\mathrm{e}^{\ln x+x}\\ \\&=&0\quad\text{car }\lim\limits_{x\rightarrow 0}(\ln x+x)=-\infty\end{array}$
Donc, $\boxed{\lim_{x\rightarrow 0}x\mathrm{e}^{x}=0}$
IV Fonctions exponentielles de base $a>0\;,\ a\neq 1$
IV.1 Définition
On appelle fonction exponentielle de base $a>0\;,\ a\neq 1$ la fonction $$g_{a}(x)=a^{x}=\mathrm{e}^{x\ln a}$$
IV.2 Étude
Soit $g_{a}$ la fonction définie par $g_{a}(x)=a^{x}=\mathrm{e}^{x\ln a}$ de courbe représentative $C_{g_{a}}.$
Alors, $D_{g_{a}}=\mathbb{R}$ et on a :
$\begin{array}{rcl}\lim\limits_{x\rightarrow -\infty}g_{a}(x)&=&\lim\limits_{x\rightarrow -\infty}\mathrm{e}^{x\ln a}\\ \\&=&\left\lbrace\begin{array}{rcl} +\infty&\text{si}&0<a<1\\0&\text{si}&a>1\end{array}\right.\end{array}$
$\begin{array}{rcl}\lim\limits_{x\rightarrow +\infty}g_{a}(x)&=&\lim\limits_{x\rightarrow +\infty}\mathrm{e}^{x\ln a}\\ \\&=&\left\lbrace\begin{array}{rcl} 0&\text{si}&0<a<1\\+\infty&\text{si}&a>1\end{array}\right.\end{array}$
Par suite,
$\centerdot\ \ $ si $0<a<1$ alors :
$\lim\limits_{x\rightarrow +\infty}\mathrm{e}^{x\ln a}=0$
Donc, la droite d'équation $y=0$ est une asymptote horizontale à $C_{g_{a}}$ en $+\infty.$
$\lim\limits_{x\rightarrow -\infty}\mathrm{e}^{x\ln a}=+\infty$
Calculons alors, $\lim\limits_{x\rightarrow -\infty}\dfrac{g_{a}(x)}{x}.$ On a :
$\begin{array}{rcl}\lim\limits_{x\rightarrow -\infty}\dfrac{g_{a}(x)}{x}&=&\lim\limits_{x\rightarrow -\infty}\dfrac{\mathrm{e}^{x\ln a}}{x}\\ \\&=&\lim\limits_{X\rightarrow +\infty}\dfrac{\mathrm{e}^{X}}{X}\ln a\quad\text{avec }X=x\ln a\\ \\&=&-\infty\end{array}$
Ainsi, $C_{g_{a}}$ admet une branche parabolique de direction $(y'Oy).$
$\centerdot\ \ $ si $a>1$ alors :
$\lim\limits_{x\rightarrow -\infty}\mathrm{e}^{x\ln a}=0$
Donc, la droite d'équation $y=0$ est une asymptote horizontale à $C_{g_{a}}$ en $-\infty.$
$\lim\limits_{x\rightarrow +\infty}\mathrm{e}^{x\ln a}=+\infty$
Calculons alors, $\lim\limits_{x\rightarrow +\infty}\dfrac{g_{a}(x)}{x}.$ On a :
$\begin{array}{rcl}\lim\limits_{x\rightarrow +\infty}\dfrac{g_{a}(x)}{x}&=&\lim\limits_{x\rightarrow +\infty}\dfrac{\mathrm{e}^{x\ln a}}{x}\\ \\&=&\lim\limits_{x\rightarrow +\infty}\dfrac{\mathrm{e}^{x\ln a}}{\mathrm{e}^{\ln x}}\\ \\&=&\lim\limits_{x\rightarrow +\infty}\mathrm{e}^{x\ln a-\ln x}\\ \\&=&\lim\limits_{x\rightarrow +\infty}\mathrm{e}^{x(\ln a-\frac{\ln x}{x})}\\ \\&=&+\infty\quad\text{car }\lim\limits_{x\rightarrow +\infty}\left(\ln a-\dfrac{\ln x}{x}\right)=\ln a>0\end{array}$
Donc, $C_{g_{a}}$ admet une branche parabolique de direction $(y'Oy).$
Soit $g'_{a}$ la fonction dérivée de $g_{a}$ alors, $$g'_{a}(x)=\left(\mathrm{e}^{x\ln a}\right)'=\ln a\times\mathrm{e}^{x\ln a}$$
Par suite, $g'_{a}(x)>0$ si, et seulement si, $a>1.$
Par conséquent, $g_{a}$ est croissante pour $a>1$ et décroissante si $0<a<1.$
Tableau de variation
$$0<a<1\qquad\qquad\qquad\quad a>1$$
$$\begin{array}{|c|lcr|}\hline x&-\infty&&+\infty\\ \hline g_{a}'(x)&&-&\\ \hline&+\infty&&\\ g_{a}&&\searrow&\\&&&0\\ \hline\end{array}\qquad\begin{array}{|c|lcr|}\hline x&-\infty&&+\infty\\ \hline g_{a}'(x)&&+&\\ \hline&&&+\infty\\ g_{a}&&\nearrow&\\&0&&\\ \hline\end{array}$$
Illustration graphique
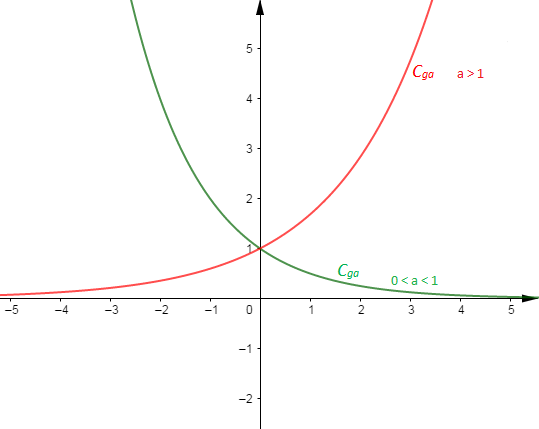
Exercice d'application
Résoudre dans $\mathbb{R}$
1) $4^{x}-3\times 2^{x+2}-2^{6}=0$
2) $2^{2x-1}+3^{x}+4^{x+\tfrac{1}{2}}-9^{\tfrac{x}{2}+1}=0$
Résolution
1) L'équation peut se mettre sous la forme $(2^{2})^{x}-3\times 2^{x}\times 2^{2}-64=0.$
Posons $X=2^{x}$ alors, l'équation devient $X^{2}-12X-64=0$
Soit $\Delta'=36+64=100$ le discriminant réduit de cette dernière équation.
On a alors deux solutions : $X_{1}=\dfrac{6-10}{1}=-4\ $ et $\ X_{2}=\dfrac{6+10}{1}=16$
Après retour sur le changement de variable, on obtient :
$\begin{array}{rcl} 2^{x}=X_{1}&\Leftrightarrow&2^{x}=-4\\ \\&\Leftrightarrow&\mathrm{e}^{x\ln 2}=-4\end{array}$
Ce qui est impossible car la fonction exponentielle est toujours positive.
$\begin{array}{rcl} 2^{x}=X_{2}&\Leftrightarrow&2^{x}=16\\ \\&\Leftrightarrow&\mathrm{e}^{x\ln 2}=16\\ \\&\Leftrightarrow&\mathrm{e}^{x\ln 2}=\mathrm{e}^{\ln 16}\\ \\&\Leftrightarrow&x\ln 2=\ln 16\\ \\&\Leftrightarrow&x=\dfrac{\ln 16}{\ln 2}\ =\ \dfrac{\ln 2^{4}}{\ln 2}\\ \\&\Leftrightarrow&x=\dfrac{4\ln 2}{\ln 2}\ =\ 4\end{array}$
D'où : $S=\{4\}$
2) On a :
$\begin{array}{rcl} 2^{2x-1}+3^{x}+4^{x+\tfrac{1}{2}}-9^{\tfrac{x}{2}+1}=0&\Leftrightarrow&2^{2x}\times\dfrac{1}{2}+3^{x}+4^{x}\times 4^{\tfrac{1}{2}}-9^{\tfrac{x}{2}}\times 9=0\\ \\ &\Leftrightarrow&4^{x}\times\dfrac{1}{2}+3^{x}+4^{x}\times 2-3^{x}\times 9=0\\ \\ &\Leftrightarrow&4^{x}\left(\dfrac{1}{2}+2\right)+3^{x}(1-9)=0\\ \\ &\Leftrightarrow&\dfrac{5}{2}\times 4^{x}-8\times3^{x}=0\\ \\ &\Leftrightarrow&5\times 4^{x}=16\times 3^{x}\\ \\ &\Leftrightarrow&5\times\mathrm{e}^{x\ln 4}=16\times\mathrm{e}^{x\ln 3}\\ \\ &\Leftrightarrow&\dfrac{\mathrm{e}^{x\ln 4}}{\mathrm{e}^{x\ln 3}}=\dfrac{16}{5}\ =\ \mathrm{e}^{\ln\tfrac{16}{5}}\\ \\ &\Leftrightarrow&\mathrm{e}^{x\ln 4-x\ln 3}=\mathrm{e}^{\ln\tfrac{16}{5}}\\ \\&\Leftrightarrow&\mathrm{e}^{x\ln\tfrac{4}{3}}=\mathrm{e}^{\ln\tfrac{16}{5}}\\ \\ &\Leftrightarrow&x\ln\tfrac{4}{3}=\ln\tfrac{16}{5}\\ \\ &\Leftrightarrow&x=\dfrac{\ln\tfrac{16}{5}}{\ln\tfrac{4}{3}}\end{array}$
D'où : $S=\left\{\dfrac{4\ln 2-\ln 5}{2\ln 2-\ln 3}\right\}$
V Fonctions puissances
V.1 Définition
On appelle fonction puissance la fonction définie sur $\mathbb{R}_{+}^{*}$ par $$f_{\alpha}(x)=x^{\alpha}=\mathrm{e}^{\alpha\ln x}\;,\quad\alpha\in\mathbb{R}$$
V.2 Étude
Soit $f_{\alpha}$ la fonction définie par $f_{\alpha}(x)=x^{\alpha}=\mathrm{e}^{\alpha\ln x}$ de courbe représentative $C_{f_{\alpha}}.$
Alors, $D_{f_{\alpha}}=]0\;;\ +\infty[$ et on a :
$\begin{array}{rcl}\lim\limits_{x\rightarrow 0^{+}}f_{\alpha}(x)&=&\lim\limits_{x\rightarrow 0^{+}}\mathrm{e}^{\alpha\ln x}\\ \\&=&\left\lbrace\begin{array}{rcl} +\infty&\text{si}&\alpha<0\\0&\text{si}&\alpha>0\end{array}\right.\end{array}$
$\begin{array}{rcl}\lim\limits_{x\rightarrow +\infty}f_{\alpha}(x)&=&\lim\limits_{x\rightarrow +\infty}\mathrm{e}^{\alpha\ln x}\\ \\&=&\left\lbrace\begin{array}{rcl} 0&\text{si}&\alpha<0\\+\infty&\text{si}&\alpha>0\end{array}\right.\end{array}$
Par suite,
$\centerdot\ \ $ si $\alpha<0$ alors :
$\lim\limits_{x\rightarrow 0^{+}}\mathrm{e}^{\alpha\ln x}=+\infty$
Donc, la droite d'équation $x=0$ est une asymptote verticale à $C_{f_{\alpha}}.$
$\lim\limits_{x\rightarrow +\infty}\mathrm{e}^{\alpha\ln x}=0$
Ainsi, la droite d'équation $y=0$ est une asymptote horizontale à $C_{f_{\alpha}}$ en $+\infty.$
$\centerdot\ \ $ si $\alpha>0$ alors :
$\lim\limits_{x\rightarrow 0^{+}}\mathrm{e}^{\alpha\ln x}=0$
Donc, la fonction $f_{\alpha}$ est prolongeable par continuité en 0 et on a : $$g_{\alpha}(x)\;=\;\left\lbrace\begin{array}{rcl} f_{\alpha}(x)&\text{si}&x>0\\0&\text{si}&x=0\end{array}\right.$$
Étudions la dérivabilité de $g_{\alpha}$ en 0. On a :
$\begin{array}{rcl}\lim\limits_{x\rightarrow 0^{+}}\dfrac{g_{\alpha}(x)-g_{\alpha}(0)}{x-0}&=&\lim\limits_{x\rightarrow 0^{+}}\dfrac{x^{\alpha}}{x}\\ \\&=&\lim\limits_{x\rightarrow 0^{+}}x^{\alpha-1}\\ \\&=&\lim\limits_{x\rightarrow 0^{+}}\mathrm{e}^{(\alpha-1)\ln x}\\ \\&=&\left\lbrace\begin{array}{rcl} +\infty&\text{si}&0<\alpha<1\\0&\text{si}&\alpha>1\end{array}\right.\end{array}$
D'où, on obtient au point d'abscisse 0 :
$-\ \ $ une demi-tangente verticale pour $0<\alpha<1$
$-\ \ $ une demi-tangente horizontale pour $\alpha>1$
Par ailleurs, $\lim\limits_{x\rightarrow +\infty}\mathrm{e}^{\alpha\ln x}=+\infty$
Calculons alors, $\lim\limits_{x\rightarrow +\infty}\dfrac{f_{\alpha}(x)}{x}.$ On a :
$\begin{array}{rcl}\lim\limits_{x\rightarrow +\infty}\dfrac{f_{\alpha}(x)}{x}&=&\lim_{x\rightarrow +\infty}x^{\alpha-1}\\ \\&=&\lim\limits_{x\rightarrow +\infty}\mathrm{e}^{(\alpha-1)\ln x}\\ \\&=&\left\lbrace\begin{array}{rcl} 0&\text{si}&0<\alpha<1\\+\infty&\text{si}&\alpha>1\end{array}\right.\end{array}$
Par conséquent, $C_{f_{\alpha}}$ admet en $+\infty$ :
$-\ \ $ une branche parabolique de direction $(x'Ox)$ pour $0<\alpha<1$
$-\ \ $ une branche parabolique de direction $(y'Oy)$ si $\alpha>1$
Soit $f'_{\alpha}$ la fonction dérivée de $f_{\alpha}$ alors, $$f'_{\alpha}(x)=\left(\mathrm{e}^{\alpha\ln x}\right)'=\dfrac{\alpha}{x}\times\mathrm{e}^{\alpha\ln x}$$
Par suite, $f'_{\alpha}(x)>0$ si, et seulement si, $\alpha>0.$
Par conséquent, $f_{\alpha}$ est croissante pour $\alpha>0$ et décroissante si $\alpha<0.$
Tableau de variation
$$\alpha<0\qquad\qquad\qquad\quad \alpha>0$$
$$\begin{array}{|c|lcr|}\hline x&0&&+\infty\\ \hline f_{\alpha}'(x)&||&-&\\ \hline&+\infty&&\\ f_{\alpha}&||&\searrow&\\&||&&0\\ \hline\end{array}\qquad\begin{array}{|c|lcr|}\hline x&0&&+\infty\\ \hline f_{\alpha}'(x)&||&+&\\ \hline&||&&+\infty\\ f_{\alpha}&||&\nearrow&\\&0&&\\ \hline\end{array}$$
Illustration graphique
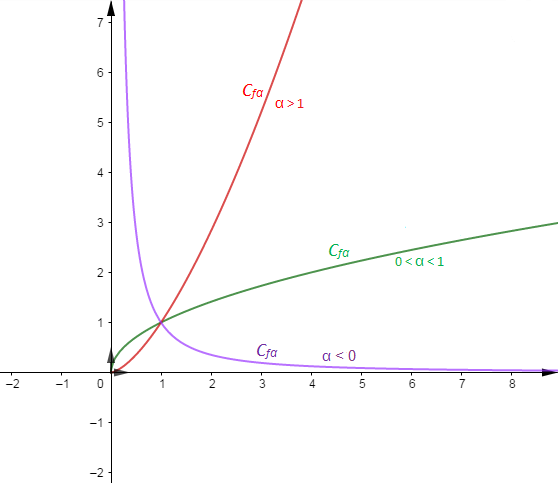
VI Croissances comparées
Dans cette partie nous allons donner des limites de référence permettant de résoudre certaines formes indéterminées qui reviennent de façon récurrente.
En $+\infty$ :
$\centerdot\ \ \lim\limits_{x\rightarrow +\infty}\dfrac{\mathrm{e}^{x}}{x}=+\infty$
$\centerdot\ \ \lim\limits_{x\rightarrow +\infty}\dfrac{\mathrm{e}^{x}}{x^{\alpha}}=+\infty\;;\ $ avec $\alpha>0$
$\centerdot\ \ \lim\limits_{x\rightarrow +\infty}\dfrac{\ln x}{x^{\alpha}}=0\;;\ $ avec $\alpha>0$
$\centerdot\ \ \lim\limits_{x\rightarrow +\infty}(x^{\alpha}\mathrm{e}^{-x})=0\;;\ $ avec $\alpha>0$
$\centerdot\ \ \lim\limits_{x\rightarrow +\infty}\dfrac{a^{x}}{x^{\alpha}}=+\infty\;;\ $ avec $\alpha>0\ \text{ et }\ a>1$
$\centerdot\ \ \lim\limits_{x\rightarrow +\infty}\dfrac{\mathrm{e}^{x}}{|P(x)|}=+\infty\;;\ $ avec $P(x)$ polynôme ; $d^{\circ}P\geq 1$
$\centerdot\ \ \lim\limits_{x\rightarrow +\infty}\dfrac{\ln x}{P(x)}=0\;;\ $ avec $P(x)$ polynôme ; $d^{\circ}P\geq 1$
En 0 :
$\centerdot\ \ \lim\limits_{x\rightarrow 0}(x^{\alpha}\ln x)=0\;;\ $ avec $\alpha>0$
En $-\infty$ :
$\centerdot\ \ \lim\limits_{x\rightarrow -\infty}(x^{\alpha}\mathrm{e}^{x})=0\;;\ $ avec $\alpha>0$
$\centerdot\ \ \lim\limits_{x\rightarrow -\infty}\left(P(x)\mathrm{e}^{x}\right)=0\;;\ $ avec $P(x)$ polynôme ; $d^{\circ}P\geq 1$
Auteur:
Diny Faye & Seyni Ndiaye

Commentaires
Maodo Malick Thiam (non vérifié)
mer, 02/15/2023 - 20:09
Permalien
Vraiment vous faites du bon
Ajouter un commentaire