Généralités sur les fonctions - 2nd

Donner les ensembles de définition des fonctions suivantes :
 

$f:\mathbb{R}\rightarrow\mathbb{R}\;;\ f(x)=x^{2}+2x$

 

$g:[0;\ +\infty[\rightarrow\mathbb{R}\;;\ g(x)=\dfrac{x}{x^{2}-1}$

 

$h:[0;\ +\infty[\rightarrow\mathbb{R}\;;\ h(x)=\sqrt{1-x}$

 

$k:[0;\ 5]\rightarrow\mathbb{R}\;;\ k(x)=\dfrac{x}{x-3}$

$ABCD$ est un rectangle de périmètre $18\;m$ et de coté variable; $AB=x.$

 

1) Exprimer $AB$ en fonction de $x.$

 

2) Soit $f(x)$ l'aire de $ABCD$. Donner l'ensemble de définition de $f$ et déterminer l'expression de $f(x).$

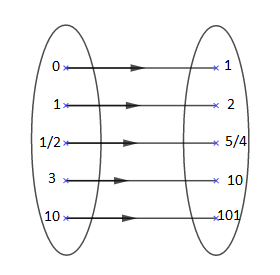
Soient $I$ et $J$deux ensembles non vides. On appelle fonction de $I$ vers $J$, toute relation qui lie, à tout élément $x$ de $I$, au plus un élément $y$ de $J$

$$\begin{array}{ccrcl} f&:&[0;\ +\infty[&\longrightarrow&\mathbb{R} \\ & &x&\longmapsto&x^{2}+1 \end{array}$$

$I=[0;\ +\infty[\;,\ J=\mathbb{R}$

 

 

 

$\centerdot\ \ $ l'ensemble $I$ est appelé de départ et $J$ l'ensemble d'arrivé.

 

$\centerdot\ \ $ $f(x)$ est l'image de $x$ par $f$

 

$\centerdot\ \ $ Si $y=f(x)$, on dit que $x$ est l'antécédent de $y$ par $f.$

 

$\centerdot\ \ $ Si $J=\mathbb{R}$, on dit que $f$ est une fonction numérique.

 

$\centerdot\ \ $ Si $I$ et $J$ sont des parties de $\mathbb{R}$, on dit que $f$ est une fonction numérique de la variable réelle.

 

$\centerdot\ \ $ $f$ définie sur $I$ par $f(x)=\ldots$ est notée parfois

$$\begin{array}{ccrcl} f&:&I&\longrightarrow&\mathbb{R} \\ & &x&\longmapsto&f(x) \end{array}$$

$f\ :\ I\rightarrow\mathbb{R}\;,\ $ l'ensemble $x\longmapsto f(x)$ de définition de $f$ noté $D_{f}$ est l'ensemble des $x$ appartenant à $I$ tels que $f(x)$ existe.
$$D_{f}=\{x\in I/f(x) \text{ existe }\}$$

Soit $(O;\ \vec{i},\ \vec{j})$, un repère orthonormé. On appelle représentation graphique d'une fonction $f$ ou graphe de $f$ ou la courbe de $f$ qu'on peut noter $\mathcal{C}_{f}\;,\ $ l'ensemble des points $M\begin{pmatrix} x\\y\end{pmatrix}$ du plan tels que $y=f(x)$

Soit $f(x)=2x^{2}-3x$ et $\mathcal{C}_{f}$ la courbe de $f.$

 

a) Parmi les points suivants quels sont ceux qui appartiennent à $\mathcal{C}_{f}$

 

$A\begin{pmatrix} 1\\ -1 \end{pmatrix}\;,\ B\begin{pmatrix} \dfrac{3}{2}\\ \\ 0 \end{pmatrix}\;,\ C\begin{pmatrix} -2\\ 2\end{pmatrix}\;,\ E\begin{pmatrix} \sqrt{2}\\ -0.2 \end{pmatrix}\;,\ F\begin{pmatrix} -6\\ 90 \end{pmatrix}$

 

b) Quels sont les points de $\mathcal{C}_{f}$ d'ordonnée 5 ?

 

c) Déterminer les coordonnées du point $G$ d'abscisse $-1$

 

d) Déterminer les points d'intersections de $\mathcal{C}_{f}$ avec les axes du repère

a) $A\begin{pmatrix} 1\\ -1 \end{pmatrix}$, on a :
 

$\begin{array}{rcl} f(x_{A})&=&f(1)\\ \\&=&2(1)^{2}-3\\ \\&=&-1\\ \\&=&y_{A}\end{array}$

 

Donc, $A\in\mathcal{C}_{f}$

 

$B\begin{pmatrix}\dfrac{3}{2}\\ \\ 0 \end{pmatrix}$, on a :
 

$\begin{array}{rcl} f(x_{B})&=&f\left(\dfrac{3}{2}\right)\\ \\ &=&2\left(\dfrac{3}{2}\right)^{2}-3\left(\dfrac{3}{2}\right)\\ \\&=&0 \\ \\ &=&y_{B} \end{array}$

 

D'où,  $B\in\mathcal{C}_{f}$

 

Soit $C\begin{pmatrix} -2\\ 2\end{pmatrix}$ alors, on a :
 

$\begin{array}{rcl} f(x_{C})&=&f(-2)\\ \\&=&2(-2)^{2}-3(-2)\\ \\&=&14\\ \\&\neq&y_{C}\end{array}$

 

D'où,  $C\notin\mathcal{C}_{f}$

 

Soit $E\begin{pmatrix} \sqrt{2}\\ -0.2 \end{pmatrix}$ alors, on a :
 

$\begin{array}{rcl} f(x_{E})&=&f(\sqrt{2})\\ \\&=&2(\sqrt{2})^{2}-3(\sqrt{2})\\ \\&=&4-3\sqrt{2}\\ \\&\neq&y_{E}\end{array}$

 

Donc, $E\notin\mathcal{C}_{f}$

 

$F\begin{pmatrix} -6\\ 90 \end{pmatrix}$ alors, on a :
 

$\begin{array}{rcl} f(x_{F})&=&f(-6)\\ \\&=&2(-6)^{2}-3(-6)\\ \\&=&90\\ \\&=&y_{F}\end{array}$

 

D'où, $F\in\mathcal{C}_{f}$

 

b) Soit $M\begin{pmatrix} x\\ y \end{pmatrix}\in\mathcal{C}_{f}\;,\ y$ est l'ordonnée de $M$ et $x$ est l'abscisse.

 

Déterminer les points d'ordonnée 5 revient à résoudre l'équation $f(x)=5.$

 

$\begin{array}{rcl} f(x)=5&\Leftrightarrow&2x^{2}-3x=5\\ \\ &\Leftrightarrow&2x^{2}-3x=5-0\end{array}$

 

$\Delta=9+40=49\ \Rightarrow\ x_{1}=\dfrac{3-7}{4}=-1\quad\text{et}\quad x_{1}=\dfrac{3+7}{4}=\dfrac{5}{2}$

 

On a donc deux points d'ordonnée 5 : $K\begin{pmatrix}\dfrac{5}{2}\\ \\ 5\end{pmatrix}\ \text{et}\ L\begin{pmatrix} -1\\ 5\end{pmatrix}$

 

c) L'ordonnée du point d'abscisse $-1$ est donnée par 

 

$f(-1)=2(-1)^{2}-3(-1)=5$ ; donc $G\begin{pmatrix} -1\\ 5\end{pmatrix}$

 

d) Pour l'intersection avec l'axe des abscisses, on résout l'équation $f(x)=0$

 

$\begin{array}{rcl} f(x)=0&\Leftrightarrow&2x^{2}-3x=0\\ \\&\Leftrightarrow&x(2x-3)=0\\ \\ &\Leftrightarrow&x=0\quad \text{ou}\quad x=\dfrac{3}{2}\end{array}$

 

Donc on a deux points d'intersection avec l'axe des abscisses : $O\begin{pmatrix} 0\\ 0\end{pmatrix}\ \text{et}\ N\begin{pmatrix} \dfrac{3}{2}\\ \\ 0\end{pmatrix}$

 

Pour l'intersection avec l'axe des ordonnées, on calcule $f(0)$

 

$f(0)=0$ alors l'origine du repère $O\begin{pmatrix} 0\\ 0\end{pmatrix}$ reste l'unique point d'intersection avec l'axe des ordonnées.

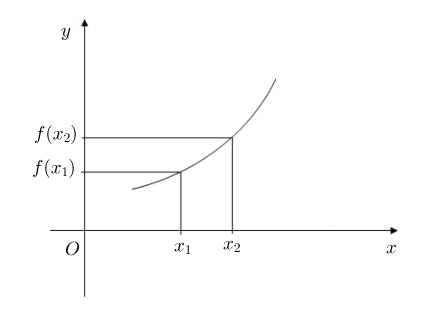
$\centerdot\ \ $ On dit qu'une fonction $f$ est croissante sur un intervalle $I$ si, et seulement si, $$\forall\;x\;,\ y\ \in I\ \text{ si }\ x\leq y\ \Rightarrow\ f(x)\leq f(y)\quad\text{ (ou si }\ x\geq y\ \Rightarrow\ f(x)\geq f(y))$$

 

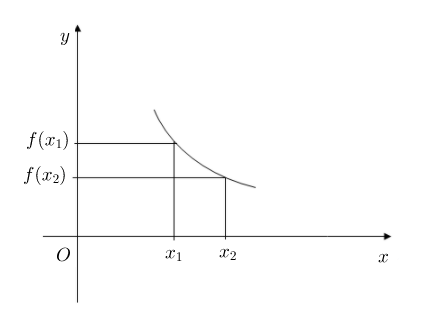
$\centerdot\ \ $ On dit qu'une fonction $f$ est décroissante sur un intervalle $I$ si, et seulement si, $$\forall\;x\;,\ y\ \in I\ \text{ si }\ x\leq y\ \Rightarrow\ f(x)\geq f(y)\quad\text{ (ou si }\ x\geq y\ \Rightarrow\ f(x)\leq f(y))$$

 

$\centerdot\ \ $ On dit qu'une fonction $f$ est constante sur un intervalle $I$ si, et seulement si, $$\forall\;x\;,\ y\ \in I\;,\ f(x)=f(y)$$

Le taux de variation d'une fonction $f$ entre $x_{1}$ et $x_{2}$ noté $$T^{x_{2}}_{x_{1}}=\dfrac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}$$

Déterminer le taux de variation de $f(x)=x^{2}$

 

On a : $$\begin{array}{rcl} T^{x_{1}}_{x_{2}}&=&\dfrac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}} \\ \\&=& \dfrac{x_{2}^{2}-x_{1}^{2}}{x_{2}-x_{1}} \\ \\ &=&\dfrac{(x_{2}-x_{1})(x_{2}+x_{1})}{x_{2}-x_{1}} \\ \\ &=&x_{2}+x_{1}\end{array}$$

Soit $T^{x_{2}}_{x_{1}}=\dfrac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}}$ le taux de variation de $x_{1}$ à $x_{2}$, d'une fonction $f$.

$\centerdot\ \ $ Si $f\text{ est }\nearrow$ alors on a : $x\leq y\ \Rightarrow\ f(x)\leq f(y)$

Ainsi, $x_{2}-x_{1}\geq 0\text{ et }f(x_{2})-f(x_{1})\geq 0\ \Rightarrow\ T^{x_{2}}_{x_{1}}\geq 0$

$\centerdot\ \ $ Si $f\text{ est }\searrow$ alors on a : $x\leq y\ \Rightarrow\ f(x)\geq f(y)$

Donc, $x_{2}-x_{1}\geq 0\text{ et }f(x_{2})-f(x_{1})\leq 0\ \Rightarrow\ T^{x_{2}}_{x_{1}}\leq 0$

En conclusion on a :

$\centerdot\ \ $ Si $T^{x_{2}}_{x_{1}}\geq 0$ sur un intervalle $I$ alors, $f\text{ est }\nearrow$ sur $I$.

$\centerdot\ \ $ Si $T^{x_{2}}_{x_{1}}\leq 0$ sur un intervalle $I$ alors, $f\text{ est }\searrow$ sur $I$.

$f(x)=x^{2}$

 

On a $f\nearrow$ sur $[0;\ +\infty[\ $ et $\ f\searrow$ sur $]-\infty;\ 0]$

 

En effet,  $T^{x_{1}}_{x_{2}}=x_{2}+x_{1}$

 

$\centerdot\ \ $ sur $[0;\ +\infty[\quad x_{1}\geq 0\:\text{ et }\:x_{2}\geq 0\;,\ $ donc, $x_{2}+x_{1}\geq 0\ \Rightarrow\ T^{x_{2}}_{x_{1}}\geq 0$

 

D'où, $\ f \text{ est croissante sur }[0;\ +\infty[$

 

$\centerdot\ \ $ sur $]-\infty;\ 0]\quad x_{1}\leq 0\:\text{ et }\:x_{2}\leq 0\;,\ $ donc, $x_{2}+x_{1}\leq 0\ \Rightarrow\ T^{x_{2}}_{x_{1}}\leq 0$

 

D'où, $\ f \text{ est décroissante sur }]-\infty;\ 0]$

 

Enfin, les variations de $f$ sont représentées dans le tableau ci-après, appelé souvent tableau de variation de $f$

$$\begin{array}{|c|lcccr|} \hline x & -\infty & & 0 & & +\infty\\ \hline &  & & & & \\ \mathrm{variations\ de\ }f & & \searrow & & \nearrow & \\ & & & 0 & & \\ \hline \end{array}$$

$\centerdot\ \ $ On dit qu'une fonction $f$ est paire si, et seulement si, les deux conditions suivantes sont vérifiées

 

$C_{1}\quad$ si $x\in D_{f}$ alors, $-x\in D_{f}$

 

$C_{2}\quad$ $\forall\;x\in D_{f};\quad f(-x)=f(x)$

 

$\centerdot\ \ $ On dit qu'une fonction $f$ est impaire si, et seulement si, les deux conditions suivantes sont vérifiées

 

$C_{1}\quad$ si $x\in D_{f}$ alors, $-x\in D_{f}$

 

$C_{2}\quad$ $\forall\;x\in D_{f};\quad f(-x)=-f(x)$

Étudier la parité des fonctions suivantes :

 

$f(x)=x^{2}-4$

 

$g(x)=x^{3}-3x$

 

$h(x)=\sqrt{x^{2}-1}$

 

$k(x)=\dfrac{x^{2}-4}{x}$

 

$f_{1}=x^{2}-4x+1$

 

$f_{2}=\dfrac{2x}{x^{2}-x}$

$f(x)=x^{2}-4\;,\quad D_{f}=\mathbb{R}$

 

Si $x\in D_{f}$ alors, $-x\in D_{f}$
 

$\begin{array}{rcl} f(-x)&=&(-x)^{2}-4\\ \\&=&x^{2}-4\\ \\&=&f(x)\end{array}$
 

Donc, $f$ est paire

 

$g(x)=x^{3}-3x\;,\quad D_{f}=\mathbb{R}$

 

Si $x\in D_{g}$ alors, $-x\in D_{g}$
 

$\begin{array}{rcl} g(-x)&=&(-x)^{3}-3(-x)\\ \\&=&-x^{3}+3x\\ \\&=&-g(x)\end{array}$
 

Donc, $g$ est impaire

 

$h(x)=\sqrt{x^{2}-1}$
 

$\begin{array}{rcl} h(x)\ \text{ existe }&\Leftrightarrow&x^{2}-1\geq 0\\ \\&\Leftrightarrow&(x-1)(x+1)\geq 0\\ \\&\Leftrightarrow&x\leq -1\ \text{ ou }\ x\geq 1\end{array}$
 

D'où, $D_{h}=]-\infty\;;\ -1]\cup[1\;;\ +\infty[$

 

Si $x\in D_{h}$ alors, $x\leq -1\ \text{ ou }\ x\geq 1\ \Rightarrow\ -x\geq 1\ \text{ ou }\ -x\leq -1$

 

Donc, $-x\in D_{h}$
 

$\begin{array}{rcl} h(-x)&=&\sqrt{(-x)^{2}-1}\\ \\&=&\sqrt{x^{2}-1}\\ \\&=&h(x)\end{array}$
 

Ainsi, la fonction $h$ est paire

 

$f_{1}=x^{2}-4x+1\;,\quad D_{f_{1}}=\mathbb{R}$

 

Si $x\in D_{f_{1}}$ alors, $-x\in D_{f_{1}}$
 

$\begin{array}{rcl} f_{1}(-x)&=&(-x)^{2}-4(-x)+1\\ \\&=&x^{2}+4x+1\\ \\&\neq&f_{1}(x)\ \text{ et }\ \neq -f_{1}(x)\end{array}$
 

Donc, $f_{1}$ n'est ni paire ni impaire

 

$f_{2}=\dfrac{2x}{x^{2}-x}$
 

$\begin{array}{rcl} f_{2}(x)\ \text{ existe }&\Leftrightarrow&x^{2}-x\neq 0\\ \\&\Leftrightarrow&x(x-1)\neq 0\\ \\&\Leftrightarrow&x\neq 0\ \text{ ou }\ x\neq 1\end{array}$
 

Par suite, $D_{f_{2}}=\mathbb{R}\setminus\{0\;;\ 1\}$

 

On a : $1\in D_{f_{2}}$ et $-1\notin D_{f_{2}}$ donc, la condition $C_{1}$ n'est pas vérifiée.

 

Par conséquent, la fonction $f_{2}$ n'est ni paire ni impaire

$\centerdot\ \ $ On dit qu'une fonction $f$ est périodique de période $T$ si, et seulement si, les deux conditions suivantes sont vérifiées

 

$C_{1}\quad$ si $x\in D_{f}$ alors $x+T\in D_{f}$

 

$C_{2}\quad$ $\forall\;x\in D_{f};\quad f(x+T)=f(x)$

$\centerdot\ \ $ Soit $\Delta$ la droite d'équation $x=a$. On dit que $\Delta$ est axe de symétrie de $\mathcal{C}_{f}$ si, et seulement si, les deux conditions suivantes sont vérifiées

 

$C_{1}\quad$ si $x\in D_{f}$ alors, $x+a\text{ et }x-a\in D_{f}$

 

$C_{2}\quad$ $\forall\;x\in D_{f};\quad f(2a-x)=f(x)$

Soit $f$ la fonction définie sur $D_{f}=\mathbb{R}$ par $f(x)=2x^{2}-5x+1.$

 

Montrer que sa représentation graphique admet comme axe de symétrie la droite $\Delta$ d'équation : $x=\dfrac{5}{4}.$

 

En effet,

$$\begin{array}{rcl} f\left(2\left(\dfrac{5}{4}\right)-x\right)&=&2\left(\dfrac{10}{4}-x\right)^{2}-5\left(\dfrac{10}{4}-x\right)+1 \\ \\&=&2\left(\dfrac{100}{16}+x^{2}-5x\right)-\dfrac{50}{4}+5x+1 \\ \\&=&\dfrac{25}{2}+2x^{2}-10x-\dfrac{25}{2}+5x+1 \\ \\&=&2x^{2}-5x+1\\ \\&=&f(x)\end{array}$$

 

Ainsi, la droite $\Delta$ d'équation : $x=\dfrac{5}{4}$ est bien axe de symétrie pour $\mathcal{C}_{f}$

 

$\centerdot\ \ $ Soit $I\begin{pmatrix} a\\b\end{pmatrix}\in\mathcal{C}_{f}$. On dit que $I$ est centre de symétrie de $\mathcal{C}_{f}$ si, et seulement si, les deux conditions suivantes sont vérifiées

 

$C_{1}\quad$ si $x\in D_{f}$ alors $x+a\text{ et }x-a\in D_{f}$

 

$C_{2}\quad$ $\forall\;x\in D_{f};\quad f(2a-x)+f(x)=2b$

Soit $f$ la fonction définie sur $D_{f}=\mathbb{R}\setminus\left\{\dfrac{5}{3}\right\}$ par $f(x)=\dfrac{2x+1}{3x-5}.$

 

Montrer que sa représentation graphique admet $I\begin{pmatrix}\dfrac{5}{3}\\ \\ \dfrac{2}{3}\end{pmatrix}$ comme centre de symétrie.

 

En effet,

$$\begin{array}{rcl} f\left(2\left(\dfrac{5}{3}\right)-x\right)+f(x)&=&\dfrac{2\left(\dfrac{10}{3}-x\right)+1}{3\left(\dfrac{10}{3}-x\right)-5}+\dfrac{2x+1}{3x-5}\\ \\&=&\dfrac{\dfrac{20}{3}-2x+1}{10-3x-5}+\dfrac{2x+1}{3x-5}\\ \\&=&\dfrac{\dfrac{23}{3}-2x}{5-3x}+\dfrac{2x+1}{3x-5}\\ \\&=&\dfrac{-\dfrac{20}{3}+4x}{3x-5}\\ \\ &=&\dfrac{12x-20}{3(3x-5)} \\ \\&=&\dfrac{4}{3}\\ \\&=&2\left(\dfrac{2}{3}\right)\end{array}$$

donc $I\begin{pmatrix}\dfrac{5}{3}\\ \\ \dfrac{2}{3}\end{pmatrix}$ est centre de symétrie pour $\mathcal{C}_{f}$

Soit $M\begin{pmatrix} x\\ f(x)\end{pmatrix}$ et $N\begin{pmatrix} -x\\ f(-x)\end{pmatrix}$ deux points de $\mathcal{C}_{f}.$

 

$\centerdot\ \ $ Si $f$ est paire alors $f(-x)=f(x)$, donc  $M\begin{pmatrix} x\\ f(x)\end{pmatrix}$ et $N\begin{pmatrix} -x\\ f(-x)\end{pmatrix}$ sont symétriques par rapport à l'axe des ordonnées $(y'Oy).$

 

D'où, si $f$ est paire alors l'axe des ordonnées est un axe de symétrie pour la courbe $\mathcal{C}_{f}.$

 

$\centerdot\ \ $ Si $f$ est impaire alors $f(-x)=-f(x)$, donc  $M\begin{pmatrix} x\\ f(x)\end{pmatrix}$ et $N\begin{pmatrix} -x\\ f(-x)\end{pmatrix}$ sont symétriques par rapport à $O$ origine du repère.

 

Ainsi, pour les fonctions impaires, l'origine du repère est un centre de symétrie pour $\mathcal{C}_{f}.$