Géométrie dans l'espace 3e

Classe: 
Troisième

I Notions de base

I.1 Règle en perspective cavalière

$\centerdot\ \ $ Les parties non visibles d'une figure dans l'espace sont représentées dans le plan en pointillés et celles visibles en traits pleins.
 
$\centerdot\ \ $ Tout segment situé dans un plan frontal (plan de face) est représenté sur le dessin en vraie grandeur (éventuellement en fonction de l'échelle donnée).
 
$\centerdot\ \ $ Il y a conservation 
 
$-\ $ du parallélisme (deux droites parallèles dans l'espace sont représentées dans l'espace par deux droites parallèles)
 
$-\ $ du milieu d'un segment (le milieu d'un segment dans l'espace est représenté dans le plan comme le milieu du segment tracé) 
 
$-\ $ des longueurs de segments parallèles (deux segments parallèles de même longueur dans l'espace sont représentés dans le plan comme étant deux segments parallèles de même longueur)
 
$\centerdot\ \ $ IL n'y a pas conservation de la mesure d'un angle si l'un des côtés ne se trouve pas dans le plan frontal.
 
$\centerdot\ \ $ Les droites perpendiculaires au plan frontal sont représentées par des droites appelées fuyantes.

Exemples :

$\centerdot\ \ $ Représentation d'un pavé-cube


 
 

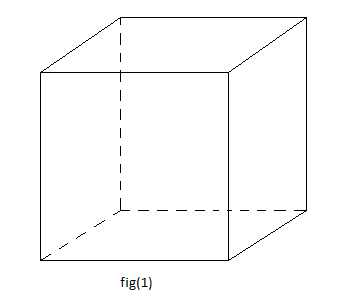
$\centerdot\ \ $ Représentation des plans parallèles sécants à une droite


 

 

$\centerdot\ \ $ Représentation des plans sécants

 
 

 

I.2 Propriétés de base

I.2.1 Droites et plans dans l'espace

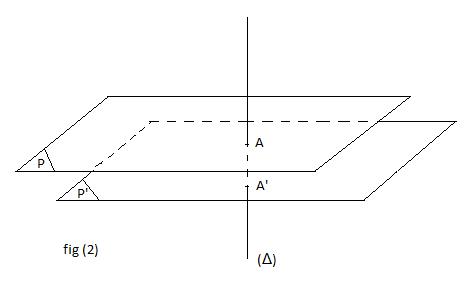
Étant donnés une droite $(\Delta)$ et un plan $\mathcal{P}$ dans l'espace.
La droite $(\Delta)$ et un plan $\mathcal{P}$ sont dits sécants s'ils n'ont qu'un seul point commun (on dira que la droite $(\Delta)$ perce le plan $\mathcal{P}).$

Exemple : voir fig.2

On a $(\Delta)\cap\mathcal{P}=A$

I.2.2 Parallélisme dans l'espace

$\centerdot\ \ $ Plans dans l'espace

Étant donnés deux plans $\mathcal{P}$ et $\mathcal{P}'$ dans l'espace.
On dira que le plan $\mathcal{P}$ est parallèle au plan $\mathcal{P}'$ s'ils sont confondus ou disjoints.

Exemple : voir fig.2

Remarque :

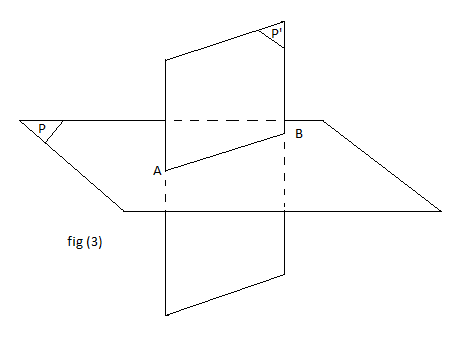
Deux plans non parallèles dans l'espace sont alors sécants et leur intersection donne alors une droite.

Exemple : voir fig.3

$\mathcal{P}\cap\mathcal{P}'=(AB)$

$\centerdot\ \ $ Droites dans l'espace

Étant données deux droites $(\Delta)$ et $(\Delta')$ dans l'espace.
La droite $(\Delta)$ est dite parallèle à la droite $(\Delta')$ si elles sont coplanaires (appartiennent à un même plan) et disjointes ou confondues.

Exemple : pavé-cube


 
 

 
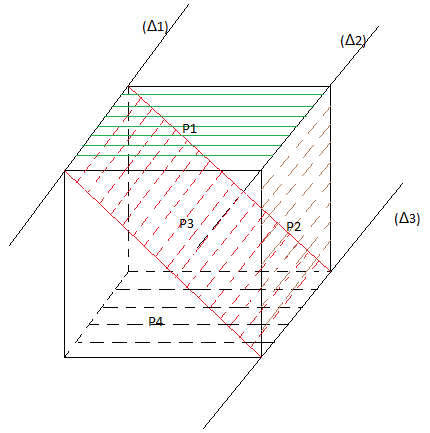
$-\ $ si deux droites sont parallèles dans l'espace, toute droite parallèle à l'une est parallèle à l'autre.
 
On a $(\Delta_{1})\parallel(\Delta_{2})$ et $(\Delta_{2})\parallel(\Delta_{3})$ alors $(\Delta_{1})\parallel(\Delta_{3})$
 
$-\ $ si deux plans sont parallèles, tout plan sécant à l'un est sécant à l'autre et les droites d'intersection sont parallèles.
 
On a $\mathcal{P}_{1}\parallel\mathcal{P}_{4}\;,\ \mathcal{P}_{1}\cap\mathcal{P}_{3}=(\Delta_{1})$ et  $\mathcal{P}_{3}\cap\mathcal{P}_{4}=(\Delta_{3})$
 
alors $(\Delta_{1})\parallel(\Delta_{3})$

I.2.3 Droites et plans perpendiculaires

$\centerdot\ \ $ Droite perpendiculaire à un plan

Soient $(\Delta)$ une droite et $\mathcal{P}$ un plan donnés dans l'espace ; $A$ leur point d'intersection.
 
La droite $(\Delta)$ est dite perpendiculaire au plan $\mathcal{P}$ si elle est perpendiculaire à toute droite de ce plan passant par leur point d'intersection $A.$

 
 

 

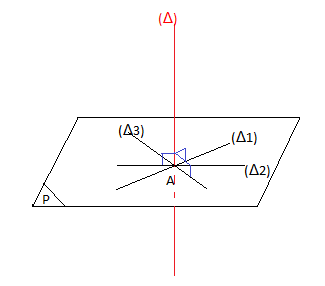
$\centerdot\ \ $ Propriété fondamentale

Si une droite est perpendiculaire à deux côtés d'un triangle, alors elle est perpendiculaire au plan du triangle.

 

 

 
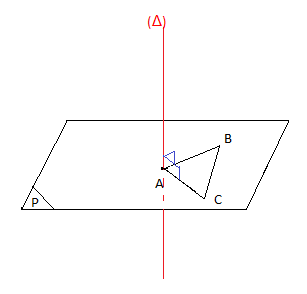
Si $(\Delta)\perp(AB)$ et $(\Delta)\perp(AC)$ alors $(\Delta)\perp(ABC)$

$\centerdot\ \ $ Droites perpendiculaires et plans parallèles 

Si deux plans sont parallèles, toute droite perpendiculaire à l'un est perpendiculaire à l'autre.

 

 
 

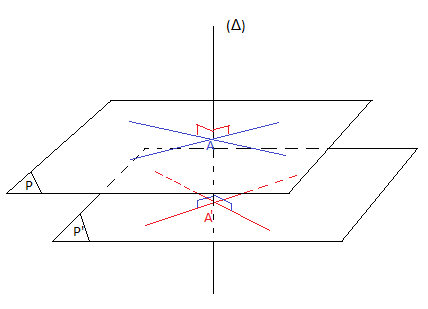
$\centerdot\ \ $ Plans perpendiculaires

Deux plans sont dits perpendiculaires dans l'espace si l'un contient une droite perpendiculaire à l'autre.

 
 

 

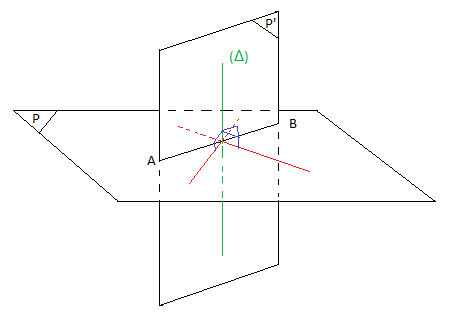
I.2.4 Application

Soit $ABCDEFGH$ un pavé-cube d'arête $4\;cm$ 
 
1) Figure

 
 

 
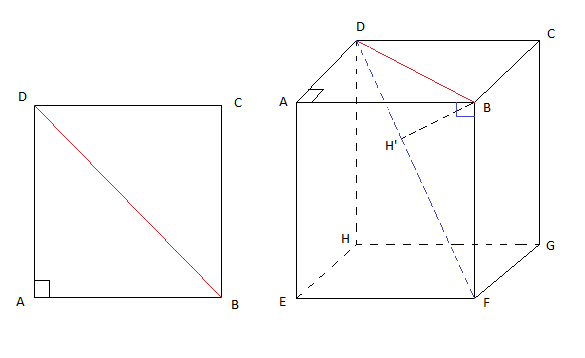
2) Calcul de $BD$
 
On a : $(AB)\perp(AD)$
 
Alors, $ABD$ est un triangle rectangle en $A$
 
d'après le théorème de Pythagore, on aura : $BD^{2}=AB^{2}+AD^{2}$
 
Donc, $BD=\sqrt{AB^{2}+AD^{2}}$
 
Ainsi, $BD=\sqrt{16+16}=\sqrt{32}$
 
D'où, $BD=4\sqrt{2}\;cm$
 
3) a) Démontrons que $BDF$ est rectangle en $B$
 
On a : $(BF)\perp(BA)$ et $(BF)\perp(BC)$
 
Alors, $(BF)\perp(ABC)$ et comme $(BD)\subset(ABC)$, donc $BDF$ est un triangle rectangle en $B$
 
b) Calcul de $DF$
 
On a : $BDF$ un triangle rectangle en $B$
 
d'après le théorème de Pythagore, on aura : $DF^{2}=BF^{2}+BD^{2}$
 
Donc, $DF=\sqrt{BF^{2}+BD^{2}}$
 
Ainsi, $DF=\sqrt{16+32}=\sqrt{48}$
 
D'où, $DF=4\sqrt{3}\;cm$
 
c) Représentation du triangle $BDF$ en vraie grandeur

 
 

 
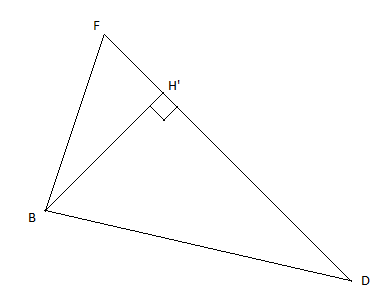
d) Calcul de $\cos\widehat{BDF}$ et $\tan\widehat{BFD}$
 
On a : $BDF$ un triangle rectangle en $B$
 
Alors, $\cos\widehat{BDF}=\dfrac{BD}{DF}$ et $\tan\widehat{BFD}=\dfrac{BD}{BF}$
 
Donc, $\cos\widehat{BDF}=\dfrac{4\sqrt{2}}{4\sqrt{3}}$ et $\tan\widehat{BFD}=\dfrac{4\sqrt{2}}{4}$
 
D'où, $\cos\widehat{BDF}=\dfrac{\sqrt{6}}{3}$ et $\tan\widehat{BFD}=\sqrt{2}$
 
4) Soit $H'$ le pied de la hauteur issue de $B$ sur $[DF]$
 
Calcul de $BH'$ et $DH'$
 
On a : $BDF$ un triangle rectangle en $B$ et $H'$ le pied de la hauteur issue de $B$ sur $[DF]$
 
Alors, $BD\times BF=BH'\times DF$ et $BD^{2}=DH'\times DF$
 
Donc, $BH'=\dfrac{BD\times BF}{DF}$ et $DH'=\dfrac{BD^{2}}{DF}$
 
Ainsi, $BH'=\dfrac{4\sqrt{2}\times 4}{4\sqrt{3}}$ et $DH'=\dfrac{32}{4\sqrt{3}}$
 
D'où, $BH'=\dfrac{4\sqrt{6}}{3}\;cm$ et $DH'=\dfrac{8\sqrt{3}}{3}$

II. Pyramide

II.1 Définition et description

On appelle pyramide, un solide constitué d'un polygone appelé base de la pyramide et dont les sommets sont reliés à un point n'appartenant pas au plan de base appelé sommet de la pyramide.

 
 

 

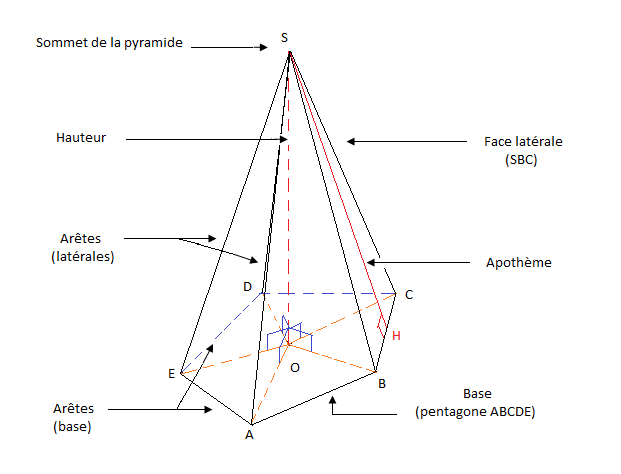
II.2 Exemple : Tétraèdre (pyramide à base triangulaire)


 

 

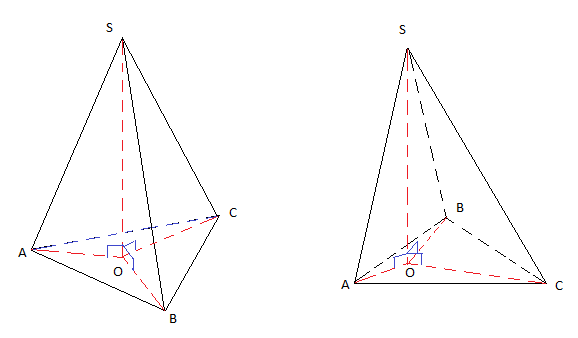
II.3 Pyramide régulière

II.3.1 Définition

On appelle polygone régulier, un polygone ayant ses côtés de même longueur et inscriptible dans un cercle.
Le centre du cercle est appelé le centre du polygone régulier.

Remarque : 

Dans un polygone régulier les angles au centre obtenus à partir de deux sommets consécutifs ont la même mesure.

 
 
 

 
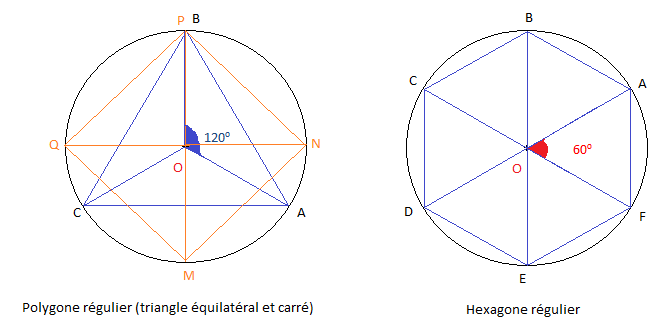
On appelle pyramide régulière, une pyramide dont la base est un polygone régulier et dont le centre du polygone est confondu au pied de la hauteur de la pyramide.

II.3.2 Exemple de pyramide régulière


 
 

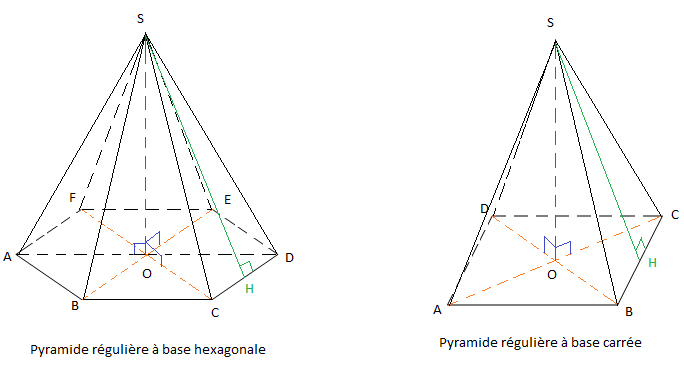
Remarque :

Dans une pyramide régulière les faces latérales sont des triangles isocèles de même aire.

III. Cône de révolution 

III.1 Définition

On appelle cône de révolution, un solide constitué d'un cercle appelé base du cône de révolution et dont les points de sa circonférence sont reliés à un point n'appartenant pas au plan de base, mais se trouvant dans l'axe du cercle de base.

III.2 Description


 

 

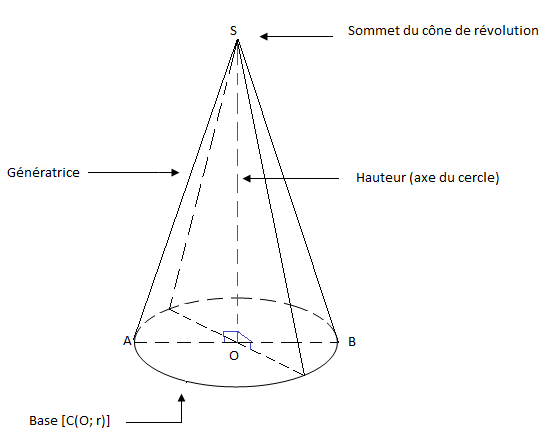
IV. Volume d'une pyramide et d'un cône de révolution

Soient $\mathcal{B}$ l'aire de base d'une pyramide ou d'un cône de révolution et $h$ leur hauteur.
 
Le volume $\mathcal{V}$ d'une pyramide ou d'un cône de révolution est donné par la relation suivante :
$$\mathcal{V}=\dfrac{\mathcal{B}\times h}{3}$$

Remarque :

Pour le cas du cône de révolution, on a :
$$\mathcal{B}=\pi\times R^{2}$$

V. Section d'une pyramide ou d'un cône de révolution parallèlement au plan de base

V.1 Section d'une pyramide régulière à base carrée


 

 
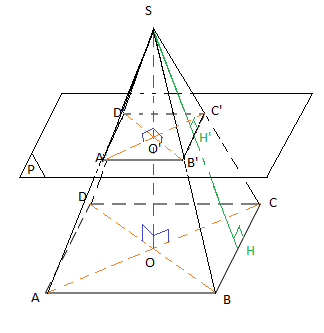
On a : $(ABC)\parallel\mathcal{P}\;,\ (ABCD)\cap(SAB)=(AB)$ et $\mathcal{P}\cap(SAB)=(A'B')$ 
 
Alors, $(AB)\parallel(A'B')$
 
Donc, $SA'B'$ et $SAB$ sont deux triangles en position de Thalès.
 
D'après le théorème de Thalès on aura : $\dfrac{SA'}{SA}=\dfrac{SB'}{SB}=\dfrac{A'B'}{AB}=k\in\mathbb{R}$
 
Par suite, $A'B'=k\times AB$
 
De manière analogue, on aura :
 
$B'C'=k\times BC\;,\ C'D'=k\times CD$ et $D'A'=k\times DA$
 
et comme $AB=BC=CD=DA$ alors, $A'B'=B'C'=C'D'=D'A'$
 
Par conséquent, $A'B'C'D'$ est un losange
 
De plus, on a : $ABD$ un triangle rectangle en $A$
 
d'après le théorème de Pythagore on aura : $BD^{2}=AB^{2}+AD^{2}$
 
Alors, $\dfrac{D'B'^{2}}{k^{2}}=\dfrac{A'B'^{2}}{k^{2}}+\dfrac{A'D'^{2}}{k^{2}}$
 
Donc, $D'B'^{2}=A'B'^{2}+A'D'^{2}$
 
D'après la réciproque du théorème de Pythagore, on aura : $(A'B'D')$ un triangle rectangle en $A'$
 
D'où, $A'B'C'D'$ un carré
 

V.2 Section d'un cône de révolution


 

 
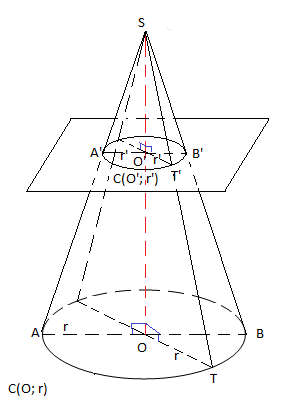
On a : $\mathcal{C}(O\;;\ r)\parallel(\mathcal{P})\;;\ (SOT)\cap\mathcal{C}(O\;;\ r)=(OT)$ et $(SOT)\cap\mathcal{P}=(O'T')$
 
Alors, $(OT)\parallel(O'T')$
 
Donc, $SO'T'$ et $SOT$ sont deux triangles en position de Thalès.
 
D'après le théorème de Thalès, on aura : $\dfrac{SO'}{SO}=\dfrac{ST'}{ST}=\dfrac{O'T'}{OT}=k\in\mathbb{R}$
 
Ainsi, $O'T'=k.OT$
 
D'où, $O'T'=k.r$
 
Si $T$ décrit le cercle $\mathcal{C}(O\;;\ r)$ alors, $T'$ décrira le cerce $\mathcal{C}'(O'\;;\ r'=k.r)$

V.3 Propriétés

$\centerdot\ \ $ La section d'une pyramide ou d'un cône de révolution par un plan parallèle au plan de base est une figure géométrique semblable à la figure de base.
 
$\centerdot\ \ $ Dans le cadre d'une réduction (ou d'un agrandissement), si les distances sont multipliées par $k$ alors les aires seront multipliées par $k^{2}$ et les volumes par $k^{3}.$

VI. Patron d'une pyramide ou d'un cône de révolution

VI.1 Patron d'une pyramide : cas d'une pyramide régulière à base carrée.

Soit $SABCD$ une pyramide régulière à base carrée $ABCD$ telle que $AB=4\;cm$ et $SA=6\;cm$
 
1) Figure 

 
 

 
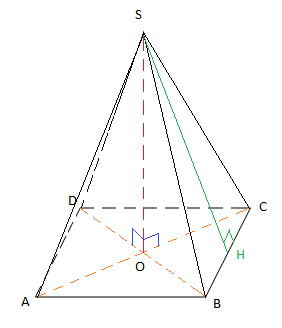
2) Calcul de $OA=OB=OC=OD$
 
On a : $AOB$ un triangle rectangle en $O$, alors $\cos\widehat{OAB}=\dfrac{OA}{AB}$ 
 
Donc, $OA=AB.\cos\widehat{OAB}$ 
 
et comme $\widehat{OAB}=45^{\circ}$
 
alors, $OA=4\times \dfrac{\sqrt{2}}{2}$ d'où : $OA=2\sqrt{2}\;cm$
 
3) Calcul de $SO$
 
On a : $SOA$ un triangle rectangle en $O$, alors $SO^{2}+OA^{2}=SA^{2}$
 
Donc, $SO^{2}=SA^{2}-OA^{2}$
 
Ainsi, $SO=\sqrt{SA^{2}-OA^{2}}$
 
$SO=\sqrt{36-8}=\sqrt{28}$
 
D'où, $SO=2\sqrt{7}\;cm$
 
4) Calcul de $SH$
 
On a : $SHB$ un triangle rectangle en $H$, alors $SH^{2}+HA^{2}=SB^{2}$
 
Donc, $SH^{2}=SB^{2}-HB^{2}$
 
Ainsi, $SH=\sqrt{SB^{2}-HB^{2}}$
 
$SH=\sqrt{36-4}=\sqrt{32}$
 
D'où, $SH=4\sqrt{2}\;cm$

 
 

 
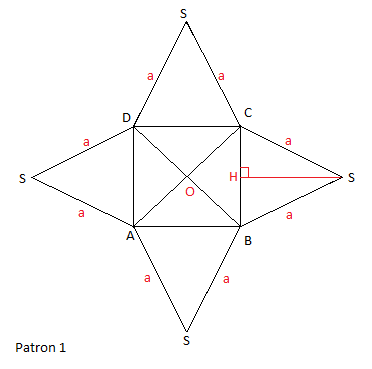
$$\boxed{\mathcal{A}=\mathcal{B}+\mathcal{A}_{L}}$$
 
$$\boxed{\mathcal{A}_{L}=4\times\mathcal{A}(SBC)\;,\quad\mathcal{A}_{L}=4\times\dfrac{BC\times SH}{2}\;,\quad\mathcal{A}_{L}=p\times\dfrac{x}{2}}$$
 
Valables seulement pour les pyramides régulières

 
 

 

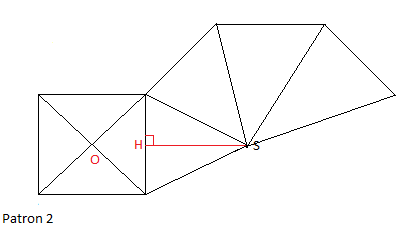
VI.2 Patron d'un cône de révolution

Soit un cône de révolution de sommet $S$ et de base le cercle $\mathcal{C}(O\;;\ r=3\;cm)$ tel que $SO=4\;cm$

 
 

 
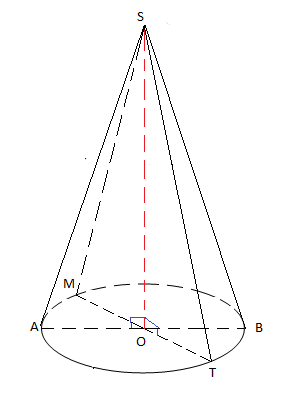
1) Calcul de $SA$
 
On a : $SOA$ un triangle rectangle en $O$
 
d'après le théorème de Pythagore, on aura : $SA^{2}=SO^{2}+OA^{2}$
 
Donc, $SA=\sqrt{SO^{2}+OA^{2}}$
 
$SA=\sqrt{16+9}=\sqrt{25}$
 
D'où, $SA=5\;cm$
 
2) Calcul de $\alpha^{\circ}$
 
On a : $2\pi r=\dfrac{\pi .x.\alpha^{\circ}}{180^{\circ}}$
 
Alors, $\alpha^{\circ}=r\times\dfrac{360^{\circ}}{x}$
 
Donc, $\alpha^{\circ}=3\times\dfrac{360^{\circ}}{5}$
 
D'où, $\alpha^{\circ}=216^{\circ}$

 

 
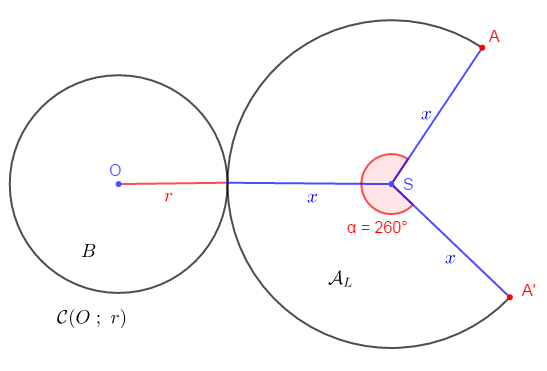
On a :
\begin{eqnarray} 360^{\circ} & \longrightarrow & \pi x^{2} \nonumber \\ \alpha^{\circ} & \longrightarrow & \mathcal{A}_{L} \nonumber\end{eqnarray}
 
Alors, $\mathcal{A}_{L}=\dfrac{\pi x^{2}\times\alpha^{\circ}}{360^{\circ}}$
 
Donc, $\mathcal{A}_{L}=\dfrac{\pi x^{2}}{360^{\circ}}\times\dfrac{r\times 360^{\circ}}{x}$
 
D'où, $$\boxed{\mathcal{A}_{L}=\pi r\times x\;\text{ ou encore }\;\mathcal{A}_{L}=\dfrac{p\times x}{2}}$$
 
Auteur: 
Abdoulaye Ba

Commentaires

Bineta Sarr (non vérifié)

ven, 04/05/2019 - 21:39

Merci beaucoup Abdoulaye

Anonyme (non vérifié)

jeu, 06/27/2019 - 21:22

Merci abdoulaye ba

benadada mohammed (non vérifié)

mar, 03/31/2020 - 17:59

merci beaucoup très bien explique encore une fois merci

Anonyme (non vérifié)

mar, 04/14/2020 - 23:26

Très bien

Stéphie (non vérifié)

ven, 04/17/2020 - 23:40

thanks you Abdoulaye

Mareme wade (non vérifié)

jeu, 07/23/2020 - 15:55

Merci beaucoup Mr Abdoulaye Bâ j'ai beaucoup comprendre la leçon en faisant les exercices

S.O.Ka (non vérifié)

ven, 07/15/2022 - 23:26

Vous êtes le meilleur monsieur

Anonyme (non vérifié)

mar, 08/11/2020 - 02:50

Ce cour est très intéressant

Anonyme (non vérifié)

dim, 04/11/2021 - 22:33

Merci beaucoup ce cour est très intéressant

Anonyme (non vérifié)

dim, 04/11/2021 - 22:33

Merci beaucoup ce cour est très intéressant

Papa oumar fall (non vérifié)

jeu, 04/22/2021 - 13:30

Excellent

Anonyme (non vérifié)

mer, 05/19/2021 - 22:42

C'est tres bien

Anonyme (non vérifié)

mer, 05/19/2021 - 22:43

C'est tres bien

Anonyme (non vérifié)

lun, 06/14/2021 - 23:41

C'est très bien

Daouda Ngom (non vérifié)

ven, 06/18/2021 - 19:05

Vraiment c'est très intéressant surtout la relation liant la génératrice le rayon de la base et l'angle de développement Merci

PRINCE SOW (non vérifié)

ven, 06/18/2021 - 23:03

mer6 ABDOULAYE

Anonyme (non vérifié)

dim, 07/17/2022 - 17:55

La leçon à beaucoup de formule

Anonyme (non vérifié)

mar, 08/06/2024 - 09:35

Merci beaucoup

Ajouter un commentaire