Géométrie dans l'espace - 5e

Classe:

Cinquième

I. Le prisme droit

I.1. Activités

Dessine un cube

$ABCDEFGH.$

Nomme les arêtes, les faces et les sommets.

Solution

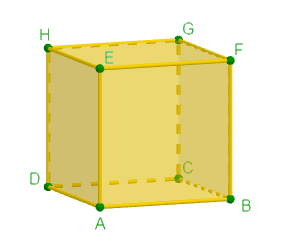
Arêtes :

$[AD]\;,\ [DH]\;,\ [FE]\;,\ [AE]\;,\ [EH]\;,\ [CG]\;,\ [DC]\;,\ [GH]\;,\ [BF]$

$\qquad\quad [AB]\;,\ [BC]\;,\ [FG]$

Faces :

$ADHE\;,\ ABCD\;,\ ABFE\;,\ FGHE\;,\ DCGH\;,\ BCGF$

Sommets :

$A\;,\ B\;,\ C\;,\ D\;,\ E\;,\ F\;,\ G\;,\ H$

I.2. La construction du prisme droit

Définition

Un prisme droit est un solide dont les faces latérales sont des rectangles et dont les bases sont des polygones réguliers superposables.

Exemple

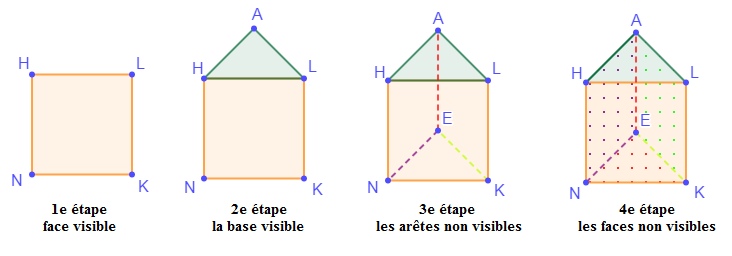
$NEKHAL$ est un prisme droit à bases triangulaires.

$[NE]\;,\ [EK]\;,\ [NK]\;,\ [HA]\;,\ [AL]\;,\ [HL]$ sont des arêtes.

$HAL\$ et

$\ NEK$ sont les bases triangulaires du prisme droit

$NEKHAL.$

Construction d'un autre prisme droit

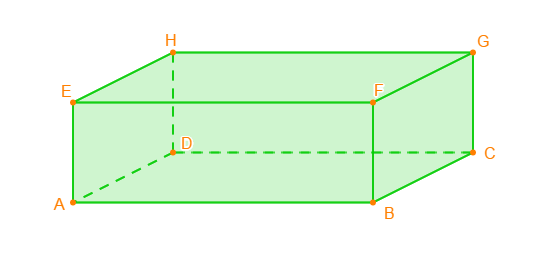
$ABCDEFGH$ est un prisme droit à bases rectangulaires. On l'appelle aussi parallélépipède rectangle.

I.3. Développement et patron du prisme droit

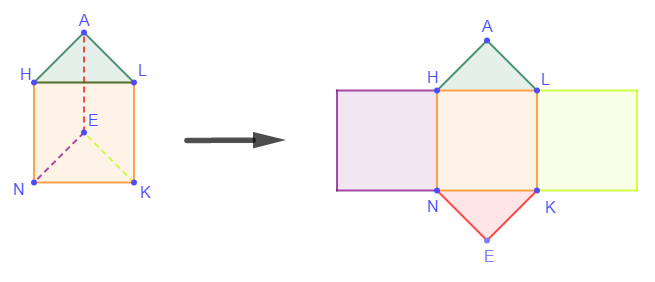
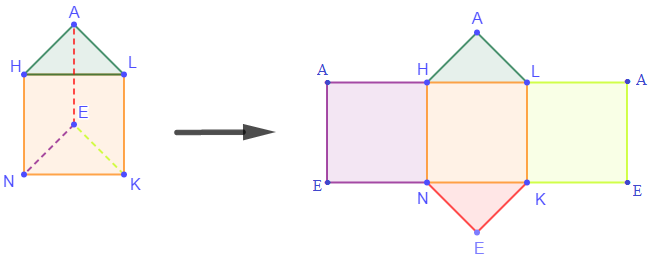
Considérons le prisme

$NEKHAL$ déjà construit, et découpons dans le sens longitudinal.

Maintenant représentons le prisme ouvert.

Exercice d'application

1) Dessine le patron d'un prisme droit dont la base est un triangle rectangle tel que les côtés perpendiculaires mesurent respectivement

$4\;cm\$ et

$\ 3\;cm$ et la hauteur

$6\;cm$

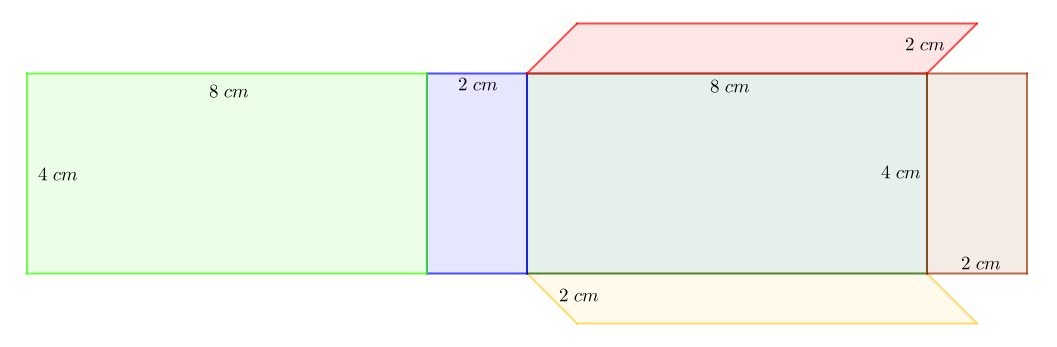
2) Dessine le patron d'un prisme droit à base rectangulaire de longueur

$8\;cm$ , de hauteur

$4\;cm$ et de largeur

$2\;cm$

Solution

1)

2)

II. Aire et volume d'un prisme droit

II.1. Aire d'un prisme droit

Pour déterminer l'aire d'un prisme droit on fait la somme de toutes les aires des faces de ce prisme.

Ainsi, l'aire d'un prisme droit est égale à la somme des aires des bases et de l'aire latérale.

Remarque : l'aire latérale est égale à la somme des aires des faces latérales du prisme.

Exemple

L'aire

$\mathcal{A}$ du prisme droit

$NEKHAL$ est donnée par :

$\mathcal{A}=\mathcal{A}_{_{HAL}}+\mathcal{A}_{_{NEK}}+\mathcal{A}_{_{AHNE}}+\mathcal{A}_{_{HLKN}}+\mathcal{A}_{_{LAEK}}$

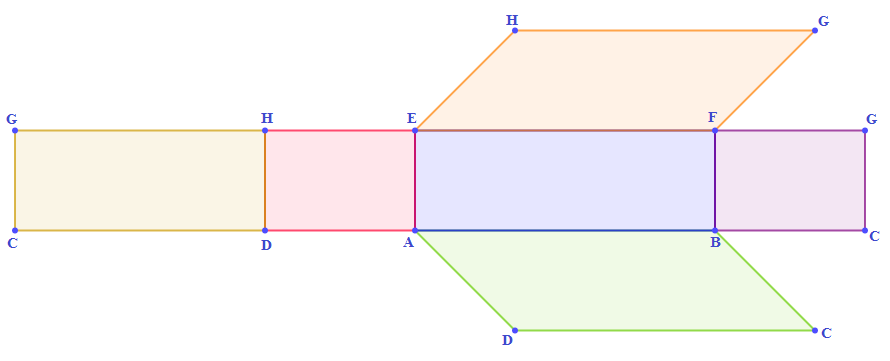
De même, l'aire du prisme droit

$ABCDEFGH$ à bases rectangulaires est donnée par :

$\mathcal{A}=\mathcal{A}_{_{ABCD}}+\mathcal{A}_{_{EFGH}}+\mathcal{A}_{_{CDHG}}+\mathcal{A}_{_{DAEH}}+\mathcal{A}_{_{ABFE}}+\mathcal{A}_{_{BCGF}}$

II.2. Volume d'un prisme droit

Pour calculer le volume

$\mathcal{V}$ d'un prisme droit, on multiplie l'aire de base par la hauteur.

$\mathcal{V}=\mathcal{A}_{_{\text{Base}}}\times\text{Hauteur}$

Exemple

Calculer le volume d'un prisme droit à base rectangulaire de longueur

$5\;cm$ , de hauteur

$3\;cm$ et de largeur

$2\;cm$

Solution

Le volume est donnée par :

$\mathcal{V}=\mathcal{A}_{_{\text{Base}}}\times\text{Hauteur}$

La base étant rectangulaire alors, l'aire de base sera donnée par :

$\begin{array}{rcl}\mathcal{A}_{_{\text{Base}}}&=&L\times\ell\\&=&5\;cm\times 2\;cm\\&=&10\;cm\end{array}$

Donc,

$\mathcal{A}_{_{\text{Base}}}=10\;cm^{2}$

Comme la hauteur est de

$3\;cm$ alors,

$\mathcal{V}=10\;cm^{2}\times 3\;cm=30\;cm^{3}$

Auteur:

Mamadou Siradji Dia

Commentaires

Anonyme (non vérifié)

mar, 10/26/2021 - 16:40

Permalien

Telecharger

répondre

sedric (non vérifié)

mar, 12/07/2021 - 10:19

Permalien

merci bcp

répondre

Anonyme (non vérifié)

mer, 04/13/2022 - 12:54

Permalien

merci beaucoup

répondre

Anonyme (non vérifié)

mer, 05/22/2024 - 00:14

Permalien

Faite des devoirs pour les

Faite des devoirs pour les profs de maths et écrivez des exercises pour les compositions

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Géométrie dans l'espace - 5e

Formulaire de recherche

I. Le prisme droit

I.1. Activités

Solution

I.2. La construction du prisme droit

Définition

Exemple

Construction d'un autre prisme droit

I.3. Développement et patron du prisme droit

Exercice d'application

Solution

II. Aire et volume d'un prisme droit

II.1. Aire d'un prisme droit

Exemple

II.2. Volume d'un prisme droit

Exemple

Solution

Commentaires

Telecharger

merci bcp

merci beaucoup

Faite des devoirs pour les

Ajouter un commentaire

Plain text