Le repérage - 5e

 

Sur une droite graduée, placez les points $A\ $ et $\ B.$ Graduez la demi-droite $[AB)$ en utilisant les nombres entiers naturels et en choisissant comme unité $[AB].$

 

Marquez les six premiers entiers naturels sur cette demi-droite graduée.

 

Soit $C$ le point de $[AB)$ d'abscisse 2. Marquez $D\;,\ E\;,\ F$ respectivement dans cet ordre.

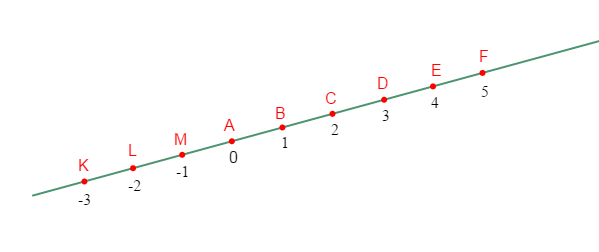
Le point $C$ a pour abscisse 2 s'écrit : $C(2)$

 

Sur cette même droite, on pouvait marquer les points $M\;,\ L\;,\ K$ d'abscisses respectifs $-1\;;\ -2\;;\ -3$

Des nombres sont opposés lorsqu'ils sont des abscisses de deux points symétriques par rapport à 'origine d'une droite graduée.

 

Le point $K$ est le symétrique du point $D$ par rapport à $A.$ Donc, $-3\ $ et $\ 3$ sont opposés.

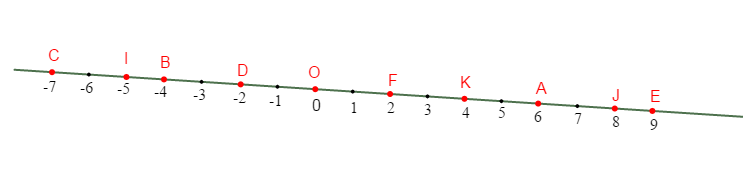
Donne les points de la droite graduée et précise l'abscisse de chaque point.

1) Range les nombres suivants dans l'ordre croissant.

 

$(+0.6)\;;\ (-0.8)\;;\ (0)\;;\ (+1)\;;\ (+2.7)\;;\ (-2.5)\;;\ (+1.4)\;;\ (-1.5)\;;\ (+2)\;;\ (-2.7)$

 

2) Soit les points $A\;,\ B\;,\ C\;,\ D\;,\ E\;,\ F\;,\ G\;,\ H\;,\ I\;,\ J$ d'abscisses respectifs des nombres décimaux relatifs cités en 1)

 

3) Représentez sur une droite graduée ces points en ayant le point $O$ comme origine et les points $K(-3)\ $ et $\ L(+3)$ comme extrémités.

1) Rangement dans l'ordre croissant :

 

$(-2.7)\;;\ (-2.5)\;;\ (-1.5)\;;\ (-0.8)\;;\ (0)\;;\ (+0.6)\;;\ (+1)\;;\ (+1.4)\;;\ (+2)\;;\ (+2.7)$
 

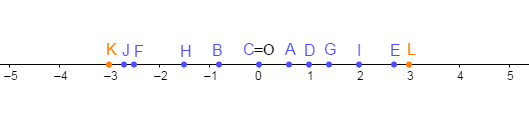
2) On a : $A(+0.6)\;;\ B(-0.8)\;;\ C(0)\;;\ D(+1)\;;\ E(+2.7)$
 

$F(-2.5)\;;\ G(+1.4)\;;\ H(-1.5)\;;\ I(+2)\;;\ J(-2.7)$
 

3) Représentation

Sur un quadrillage on a deux point $I\ $ et $\ J$

 

$-\ $ La droite $(xx')$ est appelée axe des abscisses d'origine $O$ et d'unité $OI.$

 

$-\ $ La droite $(yy')$ d'origine $O$ et d'unité $OJ$ est appelée axe des ordonnées

 

$-\ $ Les axes $(xx')\ $ et $\ (yy')$ sont perpendiculaires.

 

On note ainsi ce repère $(O\;,\ I\;,\ J)$

 

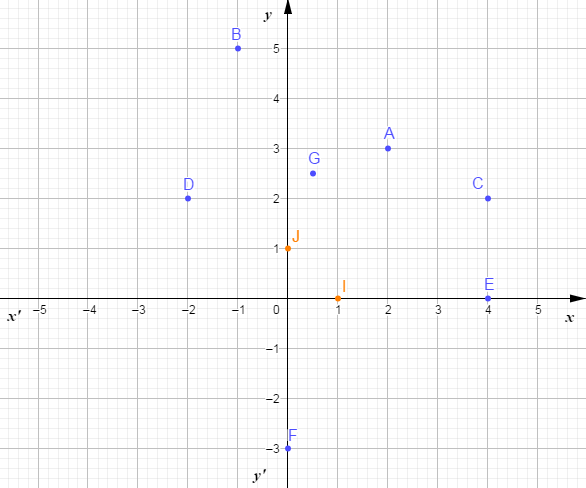
$-\ $ Plaçons les points suivants dans ce repère

 

$A\begin{pmatrix} 2\\3\end{pmatrix}\;;\ B\begin{pmatrix} -1\\5\end{pmatrix}\;;\ C\begin{pmatrix} 4\\2\end{pmatrix}\;;\ D\begin{pmatrix} -2\\2\end{pmatrix}\;;\ E\begin{pmatrix} 4\\0\end{pmatrix}\;;\ F\begin{pmatrix} 0\\-3\end{pmatrix}\;;\ G\begin{pmatrix} \dfrac{1}{2}\\ \\\dfrac{5}{2}\end{pmatrix}$