Équations et Inéquations - 5e

Classe:

Cinquième

I. Équations

I.1. Activité

Matar veut acheter un article coûtant

$2000\;F$ et il ne dispose que de

$400\;F$ Peut-il acheter l'article ?

Sinon propose-lui une solution.

Résolution

La somme dont dispose Matar est inférieur au prix de l'article. Donc, il ne pourra pas acheter cet article.

Si

$x$ est la somme qui lui manque pour pouvoir acheter l'article alors,

$\begin{array}{rcrcl} 400\;F+x=1000\;F&\Rightarrow&x&=&1\,000\;F-400\;F\\\\&\Rightarrow&x&=&600\;F\end{array}$

Donc, il lui faut

$600\;F$ de plus.

I.2. Équation de type $\ a+x=b$

Légalité

$\ a+x=b\$ où

$a\$ et

$\ b$ sont des nombres décimaux relatifs est appelée équation d'inconnue

$x.$

Trouver la valeur de

$x$ est autrement dit résoudre l'équation

$\ a+x=b.$

La solution de cette équation est :

$x=b-a$

L'ensemble des solutions est noté :

$S=\{b-a\}$

Exemple

Résoudre l'équation

$19+x=27$

Soit :

$\begin{array}{rcrcl} 19+x=27&\Rightarrow&x&=&27-19\\\\&\Rightarrow&x&=&8\end{array}$

D'où,

$\boxed{S=\{8\}}$

Application

1) Résoudre dans

$\mathbb{D}$ les équations suivantes :

a)

$12+x=15$

b)

$x+15=12$

c)

$x+19=-7$

d)

$x-12=9$

2) Modou a

$x$ cahiers dans son sac. Sa sœur lui donne 5 autres. Ce qui lui fait un total de 20 cahiers.

Trouve le nombre

$x$ de cahiers qui se trouvait dans son sac.

Solution

1) Résolvons les équations suivantes :

$\begin{array}{rcrcl}\text{a) }\ 12+x=15&\Rightarrow&x&=&15-12\\\\&\Rightarrow&x&=&3\end{array}$

Donc,

$\boxed{S=\{3\}}$

$\begin{array}{rcrcl}\text{b) }\ x+15=12&\Rightarrow&x&=&12-15\\\\&\Rightarrow&x&=&-3\end{array}$

Ainsi,

$\boxed{S=\{-3\}}$

$\begin{array}{rcrcl}\text{c) }\ x+19=-7&\Rightarrow&x&=&-7-19\\\\&\Rightarrow&x&=&-26\end{array}$

D'où,

$\boxed{S=\{-26\}}$

$\begin{array}{rcrcl}\text{d) }\ x-12=9&\Rightarrow&x&=&9+12\\\\&\Rightarrow&x&=&21\end{array}$

Donc,

$\boxed{S=\{21\}}$

2) Trouvons le nombre

$x$ de cahiers qui se trouvait dans le sac de Modou

Le problème de Modou se traduit par l'équation suivante :

$x+5=20$

Donc, trouver le nombre

$x$ revient à résoudre l'équation

$x+5=20$

On a :

$\begin{array}{rcrcl} x+5=20&\Rightarrow&x&=&20-5\\\\&\Rightarrow&x&=&15\end{array}$

D'où,

$\boxed{S=\{15\}}$

Ainsi, on peut dire que Modou avait 15 cahiers dans son sac.

I.3. Équation de type $\ ax=b$

Résoudre une équation de type

$\ ax=b\$ où

$a\$ et

$\ b$ sont des nombres décimaux relatifs avec

$a\neq 0$ , c'est trouver les valeurs de

$x$ qui vérient l'équation. La solution de cette équation est donnée par :

$x=\dfrac{b}{a}$

L'ensemble des solutions est noté :

$S=\left\{\dfrac{b}{a}\right\}$

Exemple

Soit à résoudre l'équation suivante :

$3x=27$

On a :

$\begin{array}{rcrcl} 3x=27&\Rightarrow&x&=&\dfrac{27}{3}\\ \\&\Rightarrow&x&=&9\end{array}$

Donc,

$\boxed{S=\{9\}}$

Application

Résoudre dans

$\mathbb{D}$ les équations suivantes :

a)

$2x-12=0$

b)

$3x+5=26$

c)

$2x-6=4$

Solution

$\begin{array}{rcrcl}\text{a) }\ 2x-12=0&\Rightarrow&2x&=&0+12\\ \\&\Rightarrow&x&=&\dfrac{12}{2}\\ \\&\Rightarrow&x&=&6\end{array}$

Donc,

$\boxed{S=\{6\}}$

$\begin{array}{rcrcl}\text{b) }\ 3x+5=26&\Rightarrow&3x&=&26-5\\ \\&\Rightarrow&3x&=&21\\ \\&\Rightarrow&x&=&\dfrac{21}{3}\\ \\&\Rightarrow&x&=&7\end{array}$

Par suite,

$\boxed{S=\{7\}}$

$\begin{array}{rcrcl}\text{c) }\ 2x-6=4&\Rightarrow&2x&=&4+6\\ \\&\Rightarrow&2x&=&10\\ \\&\Rightarrow&x&=&\dfrac{10}{2}\\ \\&\Rightarrow&x&=&5\end{array}$

D'où,

$\boxed{S=\{5\}}$

II. Inéquations

II.1. Inéquation de type $\ a+x\leq b$

L'inéquation

$\ a+x\leq b\$ où

$\ a\$ et

$\ b$ sont des décimaux donnés est appelée inéquation d'inconnue

$x.$

Dans une inéquation, les deux membres sont séparés par le signe de l'inégalité.

Résoudre l'inéquation

$\ a+x\leq b$ revient à déterminer l'ensemble des solutions pour la valeur de

$x\leq b-a$

Cet ensemble est noté :

$S=]-\infty\;;\ (b-a)]$

Exemple

Résoudre l'inéquation

$\ 5+x\leq 3$

On a :

$\begin{array}{rcrcl} 5+x\leq 3&\Leftrightarrow&x&\leq&3-5\\\\&\Leftrightarrow&x&\leq&-2\end{array}$

D'où,

$\boxed{S=]-\infty\;;\ -2]}$

Graphiquement, on obtient :

L'ensemble des solutions est représenté par la partie non hachurée.

II.2. Inéquation de type $\ a+x\geq b$

Résoudre l'inéquation

$\ a+x\geq b$ revient à déterminer l'ensemble des valeurs de l'inconnue

$x$ vérifiant

$x\geq b-a$

L'ensemble des solutions est noté :

$S=[(b-a)\;;\ +\infty[$

Exemple

Résoudre l'inéquation

$\ -3+x\geq -3$

On a :

$\begin{array}{rcrcl} -3+x\geq -3&\Leftrightarrow&x&\geq&-3+3\\\\&\Leftrightarrow&x&\geq&0\end{array}$

Donc,

$\boxed{S=[0\;;\ +\infty[}$

On peut aussi illustrer graphiquement cet ensemble de solution à travers la figure ci-dessous :

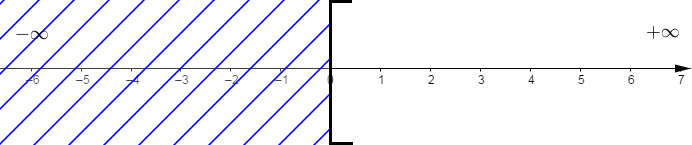
L'ensemble des solutions est représenté par la partie non hachurée.

Remarques

Soit

$a$ un nombre alors, on a :

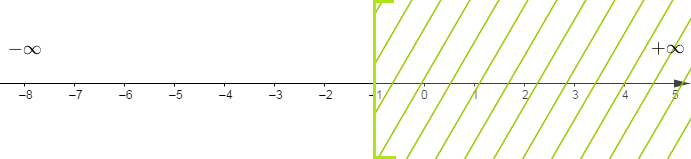
$\centerdot\$ Si

$x>a$ alors, l'ensemble des solutions

$S$ sera noté :

$S=]a\;;\ +\infty[$

Donc, le nombre

$a$ n'appartient pas à l'ensemble

$S$ des solutions.

Graphiquement, on obtient :

La partie non hachurée représente l'ensemble des solutions.

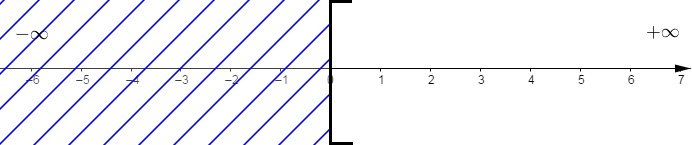
$\centerdot\$ Si

$x\geq a$ alors, l'ensemble des solutions

$S$ est donné par :

$S=[a\;;\ +\infty[$

Ici, le nombre

$a$ appartient à l'ensemble

$S$ des solutions.

La représentation graphique donne :

L'ensemble des solutions est donc représenté par la partie non hachurée.

$\centerdot\$ Si

$x<a$ alors, l'ensemble des solutions

$S$ est :

$S=]-\infty\;;\ a[$

Ainsi, le nombre

$a$ n'appartient pas à cet ensemble.

En représentant graphiquement sur une droite graduée, on obtient :

La partie non hachurée représente l'ensemble des solutions.

$\centerdot\$ Si

$x\leq a$ alors, l'ensemble des solutions

$S$ est donnée par :

$S=]-\infty\;;\ a]$

Le nombre

$a$ appartient à l'ensemble

$S$ des solutions.

La représentation graphique donne :

L'ensemble des solutions est donc représenté par la partie non hachurée.

Application

Résoudre dans

$\mathbb{D}$ les inéquations suivantes :

a)

$2(x+3)-x-5<0$

b)

$4(x-2.5)+5(3+x)\geq 5$

Solution

a) On a :

$\begin{array}{rcrcl} 2(x+3)-x-5<0&\Leftrightarrow&2\times x+2\times 3-x-5&<&0\\\\&\Leftrightarrow&2x+6-x-5&<&0\\\\&\Leftrightarrow&2x-x+6-5&<&0\\\\&\Leftrightarrow&x+1&<&0\\\\&\Leftrightarrow&x&<&-1\end{array}$

Donc,

$\boxed{S]-\infty\;;\ -1[}$

En utilisant une représentation graphique, on obtient :

Ainsi, la partie non hachurée constitue l'ensemble des solutions de cette inéquation.

b) On a :

$\begin{array}{rcl} 4(x-2.5)+5(3+x)&=&4\times x+4\times(-2.5)+5\times 3+5\times x\\\\&=&4x-10+15+5x\\\\&=&9x+5\end{array}$

Donc,

$\begin{array}{rcrcl} 4(x-2.5)+5(3+x)\geq 5&\Leftrightarrow&9x+5&\geq&5\\\\&\Leftrightarrow&9x&\geq&5-5\\\\&\Leftrightarrow&9x&\geq&0\\\\&\Leftrightarrow&x&\geq&0\end{array}$

Par suite,

$\boxed{S[0\;;\ +\infty[}$

La représentation graphique donne :

D'où, l'ensemble des solutions sera représenté par la partie non hachurée.

Auteur:

Mamadou Siradji Dia

Commentaires

Anonyme (non vérifié)

mer, 03/11/2020 - 15:19

Permalien

c'est trop bien mais il y'a

c'est trop bien mais il y'a plus de math que n'importe quel autre matière

répondre

AISSATOU SYLLA (non vérifié)

dim, 10/15/2023 - 19:54

Permalien

pourquoi, t'aime pas les

pourquoi, t'aime pas les maths?

répondre

Anonyme (non vérifié)

mer, 03/11/2020 - 15:19

Permalien

c'est trop bien mais il y'a

c'est trop bien mais il y'a plus de math que n'importe quel autre matière

répondre

Anonyme (non vérifié)

dim, 06/12/2022 - 17:55

Permalien

Trop bien cette paje ca ma

Trop bien cette paje ca ma aider

répondre

Alassan Amalkat... (non vérifié)

ven, 04/28/2023 - 19:05

Permalien

Bien

répondre

Anonyme (non vérifié)

lun, 05/22/2023 - 23:57

Permalien

Merci beaucoup pour votre

Merci beaucoup pour votre aide car en ces temps c'est difficile d'apprendre les maths

répondre

Anonyme (non vérifié)

ven, 06/02/2023 - 13:09

Permalien

Avec ça je comprends mieux

répondre

AISSATOU SYLLA (non vérifié)

dim, 10/15/2023 - 19:58

Permalien

mucha gracias sunudaara, vous

mucha gracias sunudaara, vous vous êtes surpasser pour que tous les élèves du collège au lycée puissent s'appuyer sur sunudaara afin de travailler sur nos lacunes, on adore thank you very much

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Équations et Inéquations - 5e

Formulaire de recherche

I. Équations

I.1. Activité

Résolution

I.2. Équation de type a+x=b\ a+x=b

Application

Solution

I.3. Équation de type ax=b\ ax=b

Application

Solution

II. Inéquations

II.1. Inéquation de type a+x≤b\ a+x\leq b

II.2. Inéquation de type a+x≥b\ a+x\geq b

Remarques

Application

Solution

Commentaires

Ajouter un commentaire

Plain text

I.2. Équation de type $\ a+x=b$

I.3. Équation de type $\ ax=b$

II.1. Inéquation de type $\ a+x\leq b$

II.2. Inéquation de type $\ a+x\geq b$