Les angles - 5e

Classe: 
Cinquième
 

I. Angles opposés par le même sommet

I.1. Définition

Deux angles sont dits opposés par le même sommet si les côtés de l'un sont des demi-droites deux à deux opposées aux côtés de l'autre.

I.2. Construction

Traçons deux droites $(AB)\ $ et $\ (CD)$ sécantes en $O.$

 

 
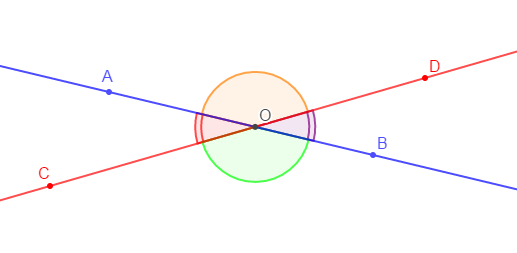
$\widehat{AOD}\ $ et $\ \widehat{COB}$ sont opposés par le même sommet $O.$
 
$\widehat{AOC}\ $ et $\ \widehat{DOB}$ sont opposés par le même sommet $O.$

I.3. Propriétés

Si deux angles sont opposés par le même sommet alors, ils ont la même mesure. Donc,
$$mes(\widehat{AOD})=mes(\widehat{COB})$$
$$mes(\widehat{DOB})=mes(\widehat{AOC})$$

II. Angles formés à partir de deux droites parallèles coupées par une sécante

II.1. Construction

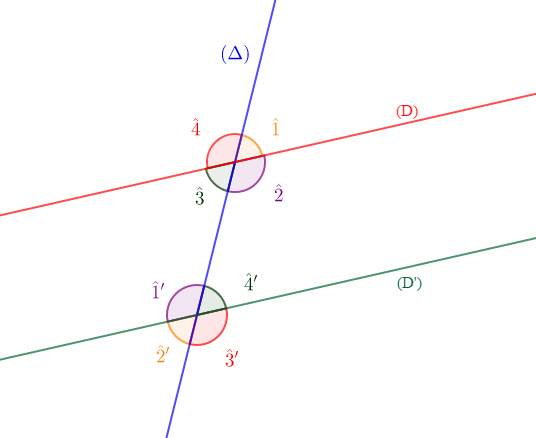
Soit $(D)\ $ et $\ (D')$ deux droites parallèles coupées par une sécante $(\Delta)$

 

 

II.2. Angles alternes externes

Deux angles sont dits alternes externes si, et seulement si :
 
$-\ \ $ Ils n'ont pas de sommet commun
 
$-\ \ $ Ils sont tous à l'extérieur de la bande délimitée par les parallèles
 
$-\ \ $ Ils sont situés de part et d'autres de la sécante

Exemple :

$\widehat{4}\ $ et $\ \widehat{3}'$ sont alternes externes, $\widehat{1}\ $ et $\ \widehat{2}'$ sont alternes externes.
 
Deux droites parallèles coupées par une sécante déterminent deux angles alternes externes de même mesure.

II.3. Angles alternes internes

On dit que deux angles sont alternes internes si, et seulement si :
 
$-\ \ $ Ils n'ont pas de sommet commun
 
$-\ \ $ Ils sont tous à l'intérieur de la bande délimitée par les parallèles
 
$-\ \ $ Ils sont également situés de part et d'autres de la sécante

Exemple :

$\widehat{2}\ $ et $\ \widehat{1}'$ sont alternes internes, $\widehat{3}\ $ et $\ \widehat{4}'$ sont alternes internes.
 
Deux droites parallèles coupées par une sécante déterminent deux angles alternes internes de même mesure.

II.4. Angles correspondants

Deux angles sont dits correspondants si, et seulement si :
 
$-\ \ $ Ils n'ont pas de sommet commun
 
$-\ \ $ Ils sont situés du même côté de la sécante
 
$-\ \ $ L'un est entre les deux droites parallèles et l'autre à l'extérieur de la bande délimitée par les parallèles

Exemple :

$\widehat{2}\ $ et $\ \widehat{3}'$ sont correspondants, $\widehat{3}\ $ et $\ \widehat{2}'$ sont correspondants.
 
Deux droites parallèles coupées par une sécante déterminent deux angles correspondants de même mesure.

III. Angles complémentaires et angles supplémentaires

III.1. Angles complémentaires

On dit que deux angles sont complémentaires si, et seulement si, la somme de leur mesure fait $90^{\circ}.$

Exemple :

Soit $\alpha=30^{\circ}\ $ et $\ \beta=60^{\circ}$, on dit que $\alpha\ $ et $\ \beta$ sont complémentaires car
$$\alpha+\beta=90^{\circ}$$

 

 
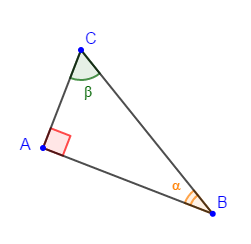
$\widehat{A}=\widehat{C}+\widehat{B}=60^{\circ}+30^{\circ}=90^{\circ}$
 
$\widehat{A}=90^{\circ}$ donc, $\widehat{B}\ $ et $\ \widehat{C}$ sont complémentaires.

III.2. Angles supplémentaires

On dit que deux angles sont supplémentaires si, et seulement si, la somme de leur mesure fait $180^{\circ}.$

Exemple :

Soit $\alpha=80^{\circ}\ $ et $\ \beta=100^{\circ}$, on dit que $\alpha\ $ et $\ \beta$ sont supplémentaires car
$$\alpha+\beta=180^{\circ}$$

 

 
$mes(\widehat{AOB})=80^{\circ}\;;\quad mes(\widehat{BOC})=100^{\circ}$
 
$\widehat{AOB}+\widehat{BOC}=\widehat{AOC}$
 
$mes(\widehat{AOC})=180^{\circ}$ donc, $\widehat{AOB}\ $ et $\ \widehat{BOC}$ sont supplémentaires.

N.B :

Soit $\widehat{a}$ un angle du plan
 
$-\ \ $ si $0^{\circ}<mes\;\widehat{a}<90^{\circ}$ alors, on dit que $\widehat{a}$ est un angle aigu.
 
$-\ \ $ si $mes\;\widehat{a}=90^{\circ}$ alors, on dit que $\widehat{a}$ est un angle droit.
 
$-\ \ $ si $90^{\circ}<mes\;\widehat{a}<180^{\circ}$ alors, on dit que $\widehat{a}$ est un angle obtus.
 
$-\ \ $ si $mes\;\widehat{a}=180^{\circ}$ alors, on dit que $\widehat{a}$ est un angle plat.
 
$-\ \ $ la somme des mesures des angles d'un triangle est toujours égale à $180^{\circ}$
 

Auteur: 
Mamadou Siradji Dia

Commentaires

Khadim dieng (non vérifié)

sam, 04/04/2020 - 09:17

Très bien

landing badji (non vérifié)

ven, 12/13/2024 - 14:14

Merci de votre effort! Je vous suggère d'ajouter les angles intérieurs de même côté supplémentaires et les angles extérieurs de même côté supplémentaire. Exemple: sur la figures on a: 2 et 4' sont des angles intérieurs du même côté et sont supplémentaires. mes (2) + mes (4')= 180° 1 et 3' sont des angles extérieurs du même côté et sont supplémentaires mes (1) + mes (3')=180° Merci!

Ajouter un commentaire