Les pyramides-4e
Classe:
Quatrième
I. Représentation d'une pyramide
Un point, appelé sommet, et un polygone, appelé base, constituent les éléments définissant une pyramide.
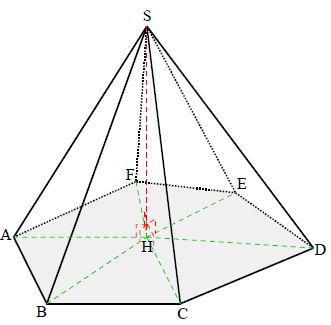
La base est le polygone $ABCDEF$
Le sommet est $S.$
Les triangles $SAB\;,\ SBC\;,\ SCD\;,\ SDE\;,\ SEF\;,\ SFA$ sont les faces latérales.
Le segment $[SH]$ est la hauteur de la pyramide.
$[SH]$ est perpendiculaire à la base donc à toutes les droites de la base , en particulier aux droites $(AH)\;,\ (BH)\;,\ (CH)\;,\ (DH)\;,\ (EH)\text{ et }(FH).$
Si la base est placée dans un plan horizontal, la hauteur $[SH]$ est une verticale.
Les triangles $SAH\;,\ SBH\;,\ SCH\;,\ SDH\;,\ SEH\;,\ SFH$ sont des triangles rectangles en $H$ ; ils définissent des plans verticaux.
Un tétraèdre (pyramide à quatre faces=pyramide à base triangulaire)
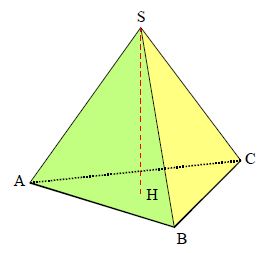
II. Pyramide régulière
Une pyramide est dite régulière si sa base est un polygone régulier
Exemple :
triangle équilatéral carré, pentagone régulier, hexagone régulier...
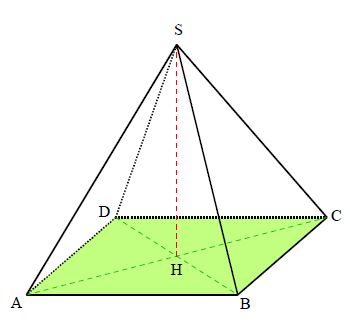
Pour la pyramide $SABCD$ ci-contre :
Sa base est le carré $ABCD.$
Son sommet est $S.$
Le pied $H$ de sa hauteur $[SH]$ est au centre du carré de base.
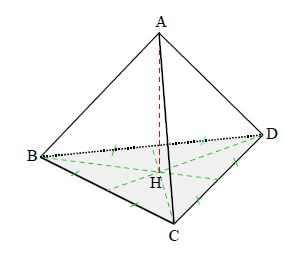
Le tétraèdre régulier
Toutes ses faces sont des triangles équilatéraux identiques ; toutes ses arêtes sont donc égales.
$ABCD$ est un tétraèdre régulier :
$ABC\;,\ ACD\;,\ ABD\;,\ BCD$ sont des triangles équilatéraux.
Ses six arêtes sont égales :
$AB=AC=AD=BC=BD=CD$
$H$, pied de la hauteur du tétraèdre, issue de $A$, est le centre de gravité du triangle $BCD.$
III. Volume de la pyramide
Les fiches précédentes ont permis d'avoir une idée du volume d'une pyramide.
D'une façon générale, le volume d'une pyramide est le tiers du volume du prisme droit qui a la même base et la même hauteur.
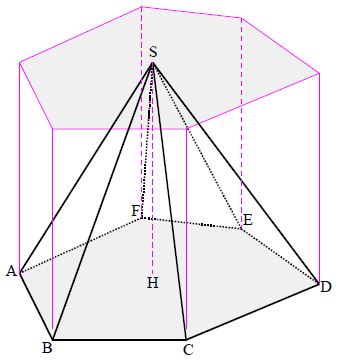
$\text{V(prisme)}=\text{Aire(base)}\times\text{hauteur}$
$\boxed{\text{V(pyramide)}=\dfrac{\text{Aire(base)}\times\text{hauteur}}{3}}$
Pour la pyramide ci-contre :
$\text{Volume}(SABCDEF)=\dfrac{\text{Aire}(ABCDEF)\times SH}{3}$
Exemple :
Volume de la pyramide $IEFGH$ dont la base est un carré de côté 4 cm et dont la hauteur mesure 4 cm.
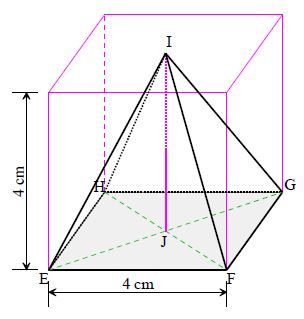
$V=\dfrac{\text{aire}(EFGH)\times\text{hauteur}}{3}$
$V=\dfrac{EF^{2}\times IJ}{3}$
$V=\dfrac{4^{2}\times 4}{3}=\dfrac{64}{3}\approx 21.3\,cm^{3}$
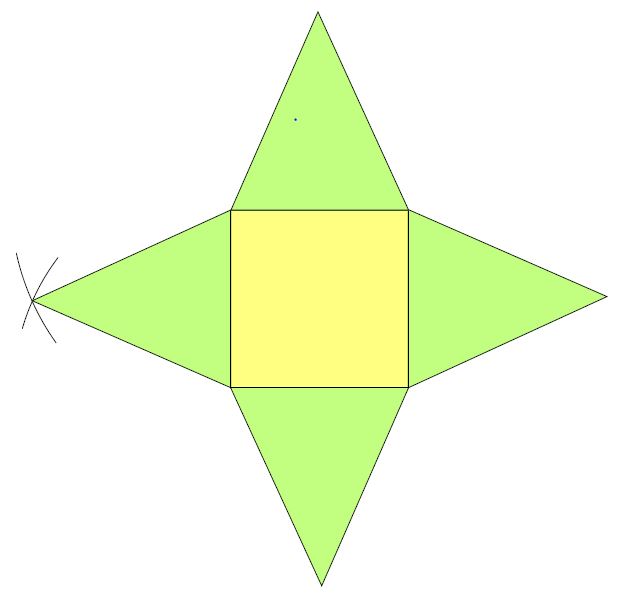
IV. Patron d'une pyramide
Pour réaliser le patron de la précédente pyramide régulière $(IEFGH)$, si sa base $EFGH$ est un carré de 4 cm de côté, il reste à calculer l'arête $IE$ :
Le triangle $IJE$ est rectangle en $J$ car $(IJ)$ est perpendiculaire au plan $EFGH$ donc à $(EJ).$
D'après la propriété de Pythagore :
$IE^{2}=IJ^{2}+EJ^{2}\qquad(1)$
$EJ$ est la moitié de la diagonale $EG$ du carré.
Le triangle $EFG$ est rectangle en $F$ ; d'après la propriété de Pythagore :
$EG^{2}=EF^{2}+FG^{2}$
$EG^{2}=4^{2}+4^{2}$
$EG^{2}=32$
Or : $EJ=\dfrac{EG}{2}$
Donc : $EJ^{2}=\left(\dfrac{EG}{2}\right)^{2}=\dfrac{EG^{2}}{2^{2}}=\dfrac{32}{4}=8\qquad(2)$
En reportant (2) dans (1) :
$IE^{2}=IJ^{2}+EJ^{2}=4^{2}+8^{2}=16+8=24$
$IE\approx 4.9\;cm$

Commentaires
Anonyme (non vérifié)
mer, 06/16/2021 - 23:29
Permalien
Cc c'est
Ajouter un commentaire