Les transformations du plan - 1er S
Classe:
Première
I. Généralités
1) Définitions
Une transformation $f$ du plan est une bijection du plan $\mathcal{P}$ vers lui-même, c'est-à-dire que tout point $M'$ du plan est l'image par $f$ d'un point $M$ unique.
\begin{eqnarray} f\ :\ \mathcal{P} &\rightarrow &\mathcal{P}\nonumber\\ M &\mapsto & M'=f(M)\nonumber \end{eqnarray}
Cela revient aussi à dire que tout point $M$ du plan a un, et un seul, antécédent par $f.$
On appelle transformation réciproque de $f$ la fonction qui, à tout point du plan, associe cet unique antécédent ; elle est notée $f^{-1}.$
$$M\stackrel{f}{\longrightarrow}M'\\\stackrel{f^{-1}}{\longleftarrow}$$
Un point $M$ est dit invariant (ou fixe) par la transformation $f$ si et seulement si $f(M)=M.$
Une figure $\mathcal{F}$ (un ensemble de points quelconque, ça peut être une droite, un cercle, un parallélogramme, ...) est dite invariante par la transformation $f$ si et seulement si :
pour tout point $M$ de $\mathcal{F}$, son image $M'=f(M)$ par $f$ appartient aussi à $\mathcal{F}.$
N.B :
On appelle image d'une figure par une transformation l'ensemble des images de tous les points de la figure.
C'est l'ensemble des points de la forme $f(M)$ lorsque $M$ décrit $\mathcal{F}$ :
$$f(\mathcal{F})=\{f(M)\;,\ M\in\mathcal{F}\}$$
On dit qu'une figure $\mathcal{F}$ est globalement invariante par la transformation $f$ si et seulement si $f(\mathcal{F})=\mathcal{F}.$
Remarque :
Dire que $\mathcal{F}$ est globalement invariante par $f$ ne signifie pas que tous les points de $\mathcal{F}$ sont fixes par $f.$
$\bullet$ Un segment $[AB]$ est globalement invariant par la symétrie centrale dont le centre est le milieu de $[AB]$,mais seul le milieu de $[AB]$ est un point fixe par cette transformation.
$\bullet$ Une droite $(AB)$ est globalement invariante par la translation de vecteur $\overrightarrow{AB}$ alors que cette transformation n'a aucun point fixe.
Définition
La transformation qui, à tout point $M$ du plan associe le point $M$ lui-même s'appelle la transformation identique ou l'identité et se note Id$\mathcal{P}$ ou Id :
Remarque :
Pour cette transformation, tous les points sont invariants.
2) Composition
Soient \begin{eqnarray} f\ :\ \mathcal{P} &\rightarrow &\mathcal{P}\nonumber\\ M &\mapsto & f(M)\nonumber \end{eqnarray} et \begin{eqnarray} g\ :\ \mathcal{P} &\rightarrow &\mathcal{P}\nonumber\\ M &\mapsto & g(M)\nonumber \end{eqnarray} deux transformations.
La composée $(f\circ g)$ est l'application :
\begin{eqnarray} f\circ g\ :\ \mathcal{P} &\rightarrow &\mathcal{P}\nonumber\\ M &\mapsto & M'=f[g(M)]\nonumber \end{eqnarray}
Théorème :
$(f\circ g)$ est une transformation du plan et sa réciproque est :
$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$
Démonstration :
Soit $M$ un point quelconque du plan.
Posons $M'=g(M)$ et $M''=f[M'].$
Alors $(f\circ g)(M)=M''.$
On a $M'=f^{-1}(M'')$ et $M=g^{-1}(M')$, d'où :
$M=g^{-1}\left[f^{-1}(M'')\right]=\left(g^{-1}\circ f^{-1}\right)(M'').$
Il en résulte que : $(f\circ g)^{-1}=f^{-1}\circ g^{-1}.$
Remarques :
$\bullet$ Si $f$, $g$ et $h$ sont trois transformations :
$$(f\circ g)\circ h=f\circ(g\circ h).$$
$\bullet$ En général $g\circ f\neq f\circ g.$
Lorsque $g\circ f=f\circ g$, on dit que les transformations $f$ et $g$ commutent.
II. Transformations usuelles
1) Translation
a) Définition
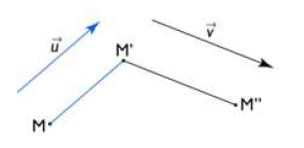
Soit $\overrightarrow{u}$ un vecteur non nul du plan.
La translation de vecteur $\overrightarrow{u}$ est l'application notée \begin{eqnarray} t_{\overrightarrow{u}}\ :\ \mathcal{P} &\rightarrow &\mathcal{P}\nonumber\\ M &\mapsto & M'\nonumber \end{eqnarray}
Le point $M$ a pour image $M'$ par la translation de vecteur $\overrightarrow{u}$ $\left(t_{\overrightarrow{u}}\ :\ M\rightarrow M'\right)$ signifie que $\overrightarrow{MM'}=\overrightarrow{u}$
b) Point invariant
$\bullet$ Si $\overrightarrow{u}\neq\overrightarrow{0}$ alors $t_{\overrightarrow{u}}$ n'a pas de point invariant (un point $M$ est invariant par $f$ s'il est confondu avec son image par $f.$)
$\bullet\bullet$ $\overrightarrow{u}=\overrightarrow{0}$ alors tout point du plan est invariant ; $t\overrightarrow{0}$ est l'application identique du plan
c) Théorème :
La translation de vecteur $\overrightarrow{u}$ est une transformation du plan et sa réciproque est la translation de vecteur $-\overrightarrow{u}.$
Démonstration :
Si $M'=t_{\overrightarrow{u}}(M)$, alors on a : $\overrightarrow{MM'}=\overrightarrow{u}$, d'où $\overrightarrow{M'M}=-\overrightarrow{u}$, donc
$$M=t_{-\overrightarrow{u}}(M')$$
d) Propriété fondamentale
Soient $A$ et $B$ deux points du plan d'images respectives $A'$ et $B'$ par la translation $t_{\overrightarrow{u}}.$
Alors, on a : $\overrightarrow{A'B'}=\overrightarrow{AB}.$
Démonstration :
D'après la relation de CHASLES, on a : $\overrightarrow{A'B'}=\overrightarrow{A'A}+\overrightarrow{AB}+\overrightarrow{BB'}.$
Or, puisque $A'=t_{\overrightarrow{u}}(A)$, on a : $\overrightarrow{A'A}=-\overrightarrow{u}$ et puisque $B'=t_{\overrightarrow{u}}(B)$, on a : $\overrightarrow{BB'}= \overrightarrow{u}.$
D'où : $\overrightarrow{A'B'}=-\overrightarrow{u}+\overrightarrow{AB}+\overrightarrow{u}=\overrightarrow{AB}.$
e) Conséquences de la propriété fondamentale
C.1 : L'image d'une droite $\mathcal{D}$ par une translation est une droite $\mathcal{D'}$ parallèle à $\mathcal{D}.$
C.2 : La translation conserve les distances c'est-à-dire que si $$\left\lbrace\begin{array}{lcl} A'&=& t_{\overrightarrow{u}}(A)\\ \\ B'&=& t_{\overrightarrow{u}}(B') \end{array}\right.$$
alors on a : $A'B'=AB.$
On dit que c'est une isométrie.
C.3 : L'image d'un cercle par une translation est un cercle de même rayon.
C.4 : Une translation conserve les barycentres, c'est-à-dire que :
si $G=bar{(A\;,\ \alpha)\ (B\;,\ \beta)}$ (avec $\alpha+\beta\neq 0)$ et si $$\left\lbrace\begin{array}{lcl} A'&=& t_{\overrightarrow{u}}(A)\\ \\ B'&=& t_{\overrightarrow{u}}(B)\;,\text{ alors}\\ \\ G'&=& t_{\overrightarrow{u}}(G) \end{array}\right.$$
$G'=bar{(A'\;,\ \alpha)\ (B'\;,\ \beta)}.$
Démonstration :
C.1 : Soit $M$ un point de la droite $(AB).$
Alors, il existe un réel $k$ tel que $\overrightarrow{AM}=k\overrightarrow{AB}.$
Mais d'après le propriété fondamentale, on alors $\overrightarrow{AM}=\overrightarrow{A'M'}$ et $\overrightarrow{AB}=\overrightarrow{A'B'}$, d'où :
$\overrightarrow{A'M'}=k\overrightarrow{A'B'}$ et par conséquent $M'\in(A'B').$
Réciproquement, soit $N_{1}$ un point de $(A'B')$ et $N$ le point tel que $t_{\overrightarrow{u}}(N)=N_{1}.$
On a $\overrightarrow{A'N_{1}}=\lambda\overrightarrow{A'B'}$ $(\lambda\in\mathbb{R})$, D'où (propriété fondamentale) : $\overrightarrow{AN}=\lambda\overrightarrow{AB}$, donc $N\in(AB).$
C.2 : D'après la propriété fondamentale, on a : $\overrightarrow{A'B'}=\overrightarrow{AB}$, d'où : $\|\overrightarrow{A'B'}\|=\|\overrightarrow{AB}\|$, soit $A'B'=AB.$
C.3 : Soit $\mathcal{C}(O\;,\ R)$ le cercle de centre $O$ et de rayon $R.$
Soit $M\in\mathcal{C}.$
On a d'après C.2 :
$O'M'=OM=r.$
D'où $M'\in\mathcal{C}(O'\;,\ R)$ avec $M'=t_{\overrightarrow{u}}(O).$
Réciproquement, soit $N_{1}\in\mathcal{C}(O'\;,\ R).$
Il existe $N\in\mathcal{P}$ tel que $t_{\overrightarrow{u}}(N)=N_{1}.$
D'où, comme $t_{\overrightarrow{u}}(O)=O'$, $ON=O'N_{1}=R\Rightarrow N\in\mathcal{C}(O\;,\ R)\mathcal{C}(O\;,\ R).$
Il en résulte que $t_{\overrightarrow{u}}\left(\mathcal{C}(O\;,\ R)\right)=\mathcal{C}(O'\;,\ R).$
C.4 : Soit $G$ le barycentre du système ${(A\;,\ \alpha)\ (B\;,\ \beta)}.$
On a (cf. chapitre sur les barycentres) :
$\overrightarrow{AG}=\dfrac{\beta}{\alpha+\beta}\overrightarrow{AB}$, d'où d'après la propriété fondamentale,
$$\overrightarrow{A'G'}=\dfrac{\beta}{\alpha+\beta}\overrightarrow{A'B'}\Leftrightarrow(\alpha+\beta)\overrightarrow{A'G'}=\beta\left(\overrightarrow{A'G'}+\overrightarrow{G'B'}\right)\Leftrightarrow\alpha\overrightarrow{G'A'}+\beta\overrightarrow{G'B'}=\overrightarrow{0};$$
f) Expression analytique
Le plan est muni d'un repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j}).$
Soit $M$ le point de coordonnées $(x\;,\ y)$, $\overrightarrow{u}$ le vecteur de coordonnées $(\alpha\;,\ \beta)$ et $M'=t_{\overrightarrow{u}}(M).$
On a alors $\overrightarrow{MM'}=\overrightarrow{u}$, ce qui, en termes de coordonnées, se traduit par :
$\left\lbrace\begin{array}{lcl} x'-x&=&\alpha\\ y'-y&=&\beta \end{array}\right.$ $\Leftrightarrow$ $\left\lbrace\begin{array}{lcl} x'&=&x+\alpha\\ y'&=&y+\beta \end{array}\right.$
$x'$ et $y'$ étant les coordonnées de $M'$ dans $(O\;,\ \vec{i}\;,\ \vec{j}).$
Le dernier système constitue une définition analytique de la translation $t_{\overrightarrow{u}}.$
Exemples :
Reconnaitre les applications de $\mathcal{P}$ vers $\mathcal{P}$ définies analytiquement par :
$$f\left\lbrace\begin{array}{lcl} x'&=&x+7\\ y'&=&y-1 \end{array}\right.$$
$$g\left\lbrace\begin{array}{lcl} x'&=&x\\ y'&=&y-8 \end{array}\right.$$
$$h\left\lbrace\begin{array}{lcl} x'&=&x+5\\ y'&=&y+3 \end{array}\right.$$
Réponses :
$f$ est la translation de vecteur $\overrightarrow{u}(7\;,\ -1)$ ; $g$ est la translation de vecteur $\overrightarrow{u}(0\;,\ -8)$ ; $h$ n'est pas une translation.
g) Composée de deux translations
Théorème :
La composée de deux translations $t_{\overrightarrow{u}}$ et $t_{\overrightarrow{v}}$ est la translation $t_{\overrightarrow{u+v}}.$
Cette composée est commutative $\left(\text{i.e }t_{\overrightarrow{v}}\circ t_{\overrightarrow{u}}=t_{\overrightarrow{v}}\circ t_{\overrightarrow{u}}\right).$
Démonstration :
Soit $M\stackrel{t_{\overrightarrow{v}}}{\rightarrow}M'\stackrel{t_{\overrightarrow{u}}}{\rightarrow}M''.$
On a $\overrightarrow{MM'}=\overrightarrow{v}$ et $\overrightarrow{M'M''}=\overrightarrow{u}.$
D'où, d'après la relation de CHASLES, $\overrightarrow{MM''}=\overrightarrow{v}+\overrightarrow{u}.$

2) Homothéties
a) Définition
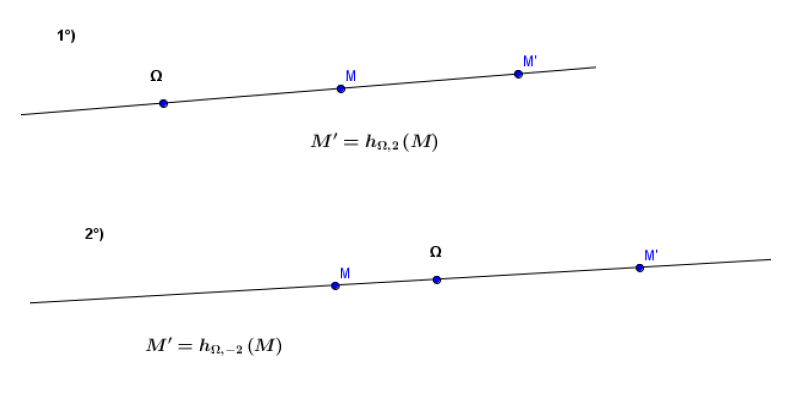
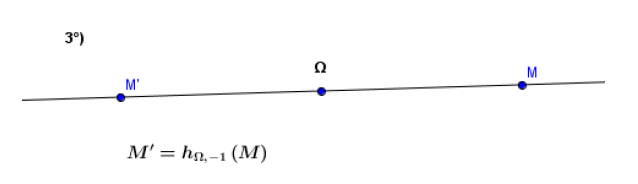
Soit $k$ un réel non nul et $\Omega$ un point du plan.
L'homothétie de centre $\Omega$ et de rapport $k$ est l'application $h_{\Omega\;,\ k}$ de $\mathcal{P}$ vers $\mathcal{P}$ définie par :
\begin{eqnarray} h_{\Omega\;,\ k}\ :\ \mathcal{P}&\longrightarrow &\mathcal{P}\nonumber\\ M&\longmapsto &M'\nonumber \end{eqnarray}
$M'$ est tel que :
$$\overrightarrow{\Omega M'}=k\overrightarrow{\Omega M}\quad(1).$$
Exemples :


Remarques :
$\bullet\ \Omega\;,\ M$ et $M'$ sont toujours alignés.
$\bullet\ h_{\Omega\;,-1}$ est la symétrie centrale de centre $\Omega.$
$\bullet\ h_{\Omega\;,1}$ est l'identité du plan $(M'=M).$
b) Points invariants
Un point $M$ est invariant par $h_{\Omega\;,k}$ si et seulement si $h_{\Omega\;,k}(M)=M$, soit $M'=M$ ou encore $\overrightarrow{\Omega M}=k\overrightarrow{\Omega M}.$
$1^{er}$ cas : Si $k=1$ :
Alors tout point $M$ est invariant.
$2^{ième}$ cas : Si $k\neq 1$ :
On a alors $(1-k)\overrightarrow{\Omega M}=\overrightarrow{0}$, soit $\overrightarrow{\Omega M}=\overrightarrow{0}$, ou encore $\Omega=M.$
Dans ce cas, $\Omega$ est le seul point invariant.
Théorème :
Toute homothétie $h_{\Omega\;,k}$ est une transformation du plan (i.e. une bijection) et la transformation réciproque est $h_{\Omega\;,\dfrac{1}{k}}.$
Démonstration :
Si $\overrightarrow{\Omega M'}=k\overrightarrow{\Omega M}$, alors $\overrightarrow{\Omega M}=\dfrac{1}{k}\overrightarrow{\Omega M}$, donc $M$ est l'image de $M'$ par $h_{\Omega\;,\dfrac{1}{k}}.$
c) Propriété fondamentale
$$\text{Si }\left\lbrace\begin{array}{lcl} A'&=&h_{\Omega\;,\ k}(M)\\ B'&=&h_{\Omega\;,\ k}(B)\;,\text{ alors }\overrightarrow{A'B'}=k\overrightarrow{AB}. \end{array}\right.$$
Démonstration :
On a par hypothèse :
$$\left\lbrace\begin{array}{lcl} \overrightarrow{\Omega A'}&=&k\overrightarrow{\Omega A}\quad(1)\\ \overrightarrow{\Omega B'}&=&k\overrightarrow{\Omega B}\quad(2)\ \;,k\text{ d'où par différence} \end{array}\right.$$
(2)-(1) et en utilisant la relation de CHASLES : $\overrightarrow{A'B'}=k\overrightarrow{AB}.$
d) Conséquences
C.1 : L'image d'une droite par une homothétie est une droite qui lui est parallèle.
C.2 : Une homothétie de rapport $k$ transforme un segment de longueur $\ell$ en un segment de longueur $|k|\times\ell.$
C.3 : $h_{\Omega\;,\ k}$ transforme le cercle $\mathcal{C}(O\;,\ R)$ en le cercle $\mathcal{C'}\left(O'\;,\ |k|\times R\right)$ avec $O'=h_{\Omega\;,\ k}(O).$
C.4 : Une homothétie conserve le barycentre.
Démonstration :
C.1 : Soit $M$ un point de la droite $(AB).$
Il existe un réel $t$ tel que $\overrightarrow{AM}=t\overrightarrow{AB}$, ce qui entraîne en multipliant les deux membres par $k$ :
$k\overrightarrow{AM}=t\left(k\overrightarrow{AB}\right).$
Or, d'après la propriété fondamentale, $\overrightarrow{A'M'}=k\overrightarrow{AM}$ et $\overrightarrow{A'B'}=k\overrightarrow{AB}$, d'où $\overrightarrow{A'M'}=t\overrightarrow{A'B'}.$
On en déduit que $M'\in(A'B').$
Réciproquement, si $M'$ est un point de la droite $(A'B')$, on a $\overrightarrow{A'M'}=t\overrightarrow{A'B'}$ pour un certain réel $t$ et en multipliant les deux membres par $\dfrac{1}{k}$, on démontre de même que $\overrightarrow{AM}=t\overrightarrow{AB}.$
Il en résulte que $h((AB))=(A'B')$ et on a $(A'B')\parallel(AB)$ puisque, d'après la propriété fondamentale, $\overrightarrow{A'B'}=k\overrightarrow{AB}.$
C.2 : Si $AB=\ell$, alors $\|\overrightarrow{AB}\|=\ell.$
Or, d'après la propriété fondamentale, $\overrightarrow{A'B'}=k$
$\overrightarrow{AB}$, donc : $A'B'=\|\overrightarrow{A'B'}\|=\|k\overrightarrow{AB}\|=|k|\times\|\overrightarrow{AB}\|=|k|\times\ell.$
C.3 : Si $M\in\mathcal{C}(O\;,\ R)$, on a $OM=R$, d'où d'après 2), $O'M'=|k|R$, donc $M'\in\mathcal{C}(O'\;,\ |k|R).$
Réciproquement, si $M'\in\mathcal{C}(O'\;,\ |k|R)$, on a $O'M'=|k|R.$
Or $O'M'=|k|OM$, d'après C.2, donc : $|k|OM=|k|R\Rightarrow OM=R\Rightarrow M\in\mathcal{C}(O\;,\ R)$
C.4 : Au cours de la preuve de C.1, nous avons établi au passage la propriété suivante :
« Si $A$, $B$ et $C$ sont trois points du plan d'images respectives $A'$, $B'$ et $C'$ par $h_{\Omega\;,k}$, et si $\overrightarrow{AB}=t\overrightarrow{AC}$, alors on a également $\overrightarrow{A'B'}=t\overrightarrow{A'C'}$ ».
On traduit cette propriété, d'ailleurs également vraie pour une translation $t_{\overrightarrow{u}}$ en disant que $h_{\Omega\;,k}$ est une application affine.
On va s'appuyer sur cela pour prouver C.4.
En effet, si $G$ est le barycentre du système ${(A\;,\ \alpha)$ ; $(B\;,\ \beta)}$, alors on a d'après les propriétés barycentriques :
$\overrightarrow{AG}=\dfrac{\beta}{\alpha+\beta}\overrightarrow{AB}$, d'où puisque $h_{\Omega\;,k}$ est une application affine, $\overrightarrow{A'G'}=\dfrac{\beta}{\alpha+\beta}\overrightarrow{A'B'}$, puis en utilisant la relation de CHASLES, on en déduit facilement (introduire $G'$ dans $\overrightarrow{A'B'}$) que $G'$ est le barycentre du système ${(A'\;,\ \alpha)\;; \ (B'\;,\ \beta)}.$
Il en résulte en particulier qu'une homothétie $h_{\Omega\;,k}$ conserve les milieux, en ce sens que si un point $I$ est le milieu du segment $[AB]$, alors $I'=h_{\Omega\;,k}(I)$ est le milieu du segment $[A'B']$, avec $A'=h_{\Omega\;,k}(A)$ et $B'=h_{\Omega\;,k}(B).$
e) Composée de deux homothéties de même centre
Théorème :
La composée de deux homothéties $h_{\Omega\;,k_{1}}$ et $h_{\Omega\;,k_{2}}$ de même centre $\Omega$ est commutative et est l'homothétie de centre $\Omega$ et de rapport $k_{1}k_{2}$ :
$$h_{\Omega\;,k_{1}}\circ h_{\Omega\;,k_{2}}=h_{\Omega\;,k_{2}}\circ h_{\Omega\;,k_{1}}=h_{\Omega\;,k_{1}k_{2}}$$
Démonstration :
Soit $M\stackrel{h_{\Omega\;,k_{2}}}{\rightarrow}M_{1}\stackrel{h_{\Omega\;,k_{1}}}{\rightarrow}M'.$
Si $M_{1}=h_{\Omega\;,k_{2}}(M)$ et $M'=h_{\Omega\;,k_{1}}(M_{1})$, on a :
$\overrightarrow{\Omega M_{1}}=k_{2}\overrightarrow{\Omega M}$ et $\overrightarrow{\Omega M'}=k_{1}\overrightarrow{\Omega M_{1}}$, d'où $\overrightarrow{\Omega M'}=k_{1}\left(k_{2}\overrightarrow{\Omega M}\right)=k_{1}k_{2}\overrightarrow{\Omega M}.$
Donc $M'=h_{\Omega\;,k_{1}k_{2}}(M).$
N.B :
La composée de deux homothéties de centres différents sera étudiée en exercice (voir plus bas).
f) Expression analytique
Le plan est muni d'un repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
Soit $M(x\;,\ y)$, $\Omega(\alpha\;,\ \beta)$ et $M'(x'\;,\ y')$ l'image de $M$ par $h_{\Omega\;,k}.$
L'égalité $\overrightarrow{\Omega M'}=k\overrightarrow{\Omega M}$ se traduit, en termes de coordonnées, par le système :
$$\left\lbrace\begin{array}{lcl} x'-\alpha&=&k(x-\alpha)\\ y'-\beta&=&k(y-\alpha) \end{array}\right.$$ équivalent à : $\left\lbrace\begin{array}{lcl} x'&=&k(x-\alpha)+\alpha\\ y'&=&k(y-\alpha)+\beta \end{array}\right.$
Ce dernier système est une définition analytique de l'homothétie $h_{\Omega\;,k}.$
3) Symétries axiales
a) Définition
Soient $\mathcal{D}$ et $\Delta$ deux droites non parallèles.
La symétrie d'axe $\mathcal{D}$ et de direction $\Delta$ est l'application \begin{eqnarray} S\ :\ \mathcal{P} &\rightarrow &\mathcal{P}\nonumber\\ M&\mapsto & M'\nonumber \end{eqnarray}
$M'$ est défini de la manière suivante :
« Soit $M_{1}$ l'intersection de $\mathcal{D}$ avec la parallèle à $\Delta$ passant par $M.$
Alors $M'$ est le symétrique de $M$ par rapport à $M_{1}.$ »
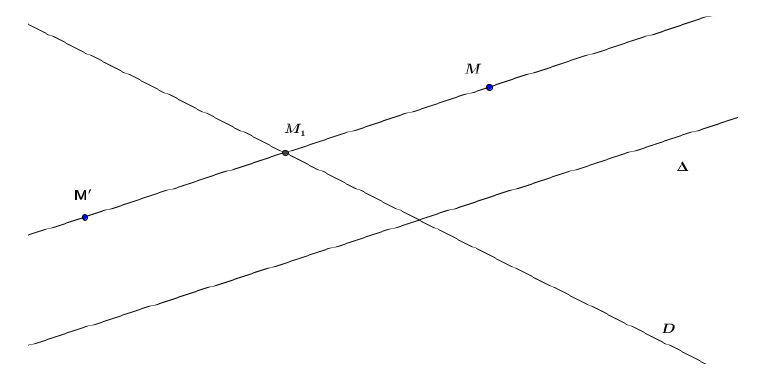
Cas particulier :
Si $\mathcal{D}$ et $\Delta$ sont perpendiculaires, on parle de symétrie orthogonale ou réflexion d'axe $\mathcal{D}.$
b) Réflexion
Définition :
Le point $M$ a pour image $M'$ par la réflexion d'axe $\Delta$ $\left(s_{(\Delta)}\ :\ M\mapsto M'\right)$ signifie que :
$-\ \ $ Si $M\not\in(\Delta)$, $\Delta$ est la médiatrice de $[MM']$
$-\ \ $ Si $M\in(\Delta)$, $M=M'$
Point invariant :
Les points invariants de $s_{(\Delta)}$ sont les points de $\Delta.$
c) Propriétés
P.1 Toute symétrie axiale $S$ est une transformation du plan (c'est-à-dire une bijection) et sa réciproque est $S^{-1}=S.$
(On traduit cette propriété en disant que $S$ est involutive.
On a donc : $S\circ S=Id\mathcal{P}$)
P.2 L'image d'une droite est une droite.
P.3 Toute réflexion est une isométrie :
en particulier ; l'image d'un cercle est un cercle de même rayon.
4) Rotation
a) Définition
Soit $O$ un point donné du plan et $\alpha$ un réel donné.
Le point $M$ a pour image le point $M'$ par la rotation de centre $O$ et d'angle $\alpha$
$\left(r_{(O\;,\alpha)}\ :\ M\rightarrow M'\right)$ signifie que
$-\ \ $ Si $M\neq O$ alors $OM=OM'$ et $\left(\overrightarrow{OM}\;;\ \overrightarrow{OM'}\right)=\alpha[2\pi]$
$-\ \ $ Si $M=O$ alors $M=M'$
Le point $O$ et le réel $\alpha$ sont appelés éléments caractéristiques de $r_{(O\;,\alpha)}$
b) Cas particuliers
$r_{(O\;,0)}$ est l'application identique du plan. (rotation d'angle nul)
$r_{(O\;,\pi)}$ (rotation de centre $O$ et d'angle $\pi$) est la symétrie centrale de centre $O.$
c) Point invariant :
$-\ \ $ Si $\alpha\neq 0+2k\pi$ alors le centre $O$ est le seul point invariant
$-\ \ $ Si $\alpha=0+2k\pi$, alors tout point du plan est invariant ;
d) Transformation réciproque :
Comme $OM'=OM$ et $\left(\overrightarrow{OM'}\;;\ \overrightarrow{OM}\right)=-\alpha\;,\ r_{(O\;,\alpha)}$ est bijective.
La transformation réciproque de $r_{(O\;,\alpha)}$ est la rotation de centre $O$ et d'angle $-\alpha$ et $r_{(O\;,\alpha)^{-1}}=r_{(O\;,-\alpha)}$
Cas particulier :
la est la symétrie de centre O.
III. Propriétés des transformations
Nous admettons tous les résultats ci-dessous :
a) Isométrie
Donnons d'abord la définition d'une isométrie :
Soit $f$ une application du plan dans lui-même.
On dit que $f$ est une isométrie du plan si pour tous points $M$ et $N$ d'images respectives $M'$ et $N'$, on a $MN=M'N'.$
$\bullet$ Les translations, les réflexions et les rotations sont des isométries
Elles conservent les distances et donc les aires et les volumes.
$\bullet$ Si $k\not\in{-1\;;\ 1}$ alors l'homothétie $h_{(O\;,k)}$ n'est pas une isométrie, les distances sont multipliées par $|k|$, les aires par $k^{2}$ et les volumes par $|k|^{3}$
b) Image d'un point d'intersection de deux figures
Soit une transformation $f$, deux figures $F_{1}$ et $F_{2}$ se coupant en $M.$
Alors $M'$, image de $M$ par la transformation $f$, est l'intersection des figures $F'_{1}=f(F_{1})$ et $F'_{2}=f(F_{2})$
c) Images de points alignés
Théorème :
Soient $A$, $B$ et $C$ trois points et $\lambda$ un nombre réel tel que $\overrightarrow{AC}=\lambda\overrightarrow{AB}.$
$A'$, $B'$ et $C'$ leurs images respectives par une translation, une réflexion, une rotation ou une homothétie alors $\overrightarrow{A'C'}=\lambda\overrightarrow{A'B'}$
N.B :
On exprime ces propriétés en disant que ces transformations sont des applications affines.
Conséquences :
L'image du milieu de $[AB]$ est le milieu de $[A'B']\left(\lambda=\dfrac{1}{2}\right)$
$-\ \ $ l'image du segment $[AB]$ est le segment $[A'B'](\lambda\in[0\;;\ 1])$
$-\ \ $ L'image de la droite $(AB)$ est la droite $(A'B')(\lambda\in\mathbb{R})$
d) Images de figure usuelles
Par une translation, une réflexion, une homothétie ou une rotation, l'image d'une figure $F$ (droite, triangle, cercle, parallélogramme, losange, rectangle, carré, etc ...) est une figure $F'$ de même nature.
Notamment, si $f$ est l'une de ces transformations, on a les résultats suivants :
1. l'image du segment $[AB]$ est le segment $[f(A)f(B)]$
2. l'image de la droite $(AB)$ est la droite $(f(A)f(B))$
3. l'image du cercle de centre $\Omega$ et de rayon $R$ est le cercle de centre $f(\Omega)$ et de rayon $R$ (ou $|k|R$ dans le cas d'une homothétie).
Ces transformations conservent :
$\bullet$ le parallélisme : Deux droites parallèles ont pour images deux droites parallèles.
$\bullet$ l'orthogonalité : Deux droites perpendiculaires ont pour images deux droites perpendiculaires.
$\bullet$ les angles géométriques : Si $A'=f(A)$ ; $B'=f(B)$ et $C'=f(C)$ : $\widehat{ABC}=\widehat{A'B'C'}$
$\bullet$ le contact entre figures (tangentes) : Si une droite $\mathcal{D}$ est tangente à un cercle $\mathcal{C}$ en $A$, son image $D'$ par $f$ est tangente à $\mathcal{C}=f(\mathcal{C})$ en $A'=f(A).$
Une translation, une rotation, une homothétie conservent les angles orientés tandis qu'une réflexion transforme un angle orienté en son opposé (on dit qu'elle contrarie les angles orientés).
Définition :
Une isométrie qui conserve l'orientation des angles est un déplacement.
Définition :
Une isométrie qui inverse l'orientation des angles est un antidéplacement.
Théorème :
La composée de deux déplacements ou de deux antidéplacements est un déplacement.
Théorème :
La composée d'un déplacement et d'un antidéplacement (peu importe l'ordre) est un antidéplacement.
IV. Composée de deux réflexions d'axes $\Delta_{1}$ et $\Delta_{2}$
1) Cas où les axes $\Delta_{1}$ et $\Delta_{2}$ sont parallèles
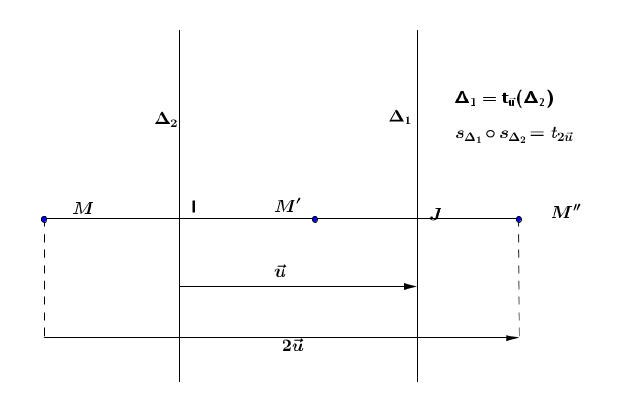
Théorème :
Si $S_{\Delta_{1}}$ et $S_{\Delta_{2}}$ sont deux réflexions d'axes respectifs $\Delta_{1}$ et $\Delta_{2}$, tels que $\Delta_{1}\parallel\Delta_{2}$, la composée $S_{\Delta_{1}}\circ S_{\Delta_{2}}$ est la translation de vecteur $2\overrightarrow{u}$, $\overrightarrow{u}$ étant le vecteur tel que $\Delta_{1}=t_{\overrightarrow{u}}(\Delta_{2}).$
Démonstration :
Soit $M'=S_{\Delta_{2}}(M)$, $M''=S_{\Delta_{1}}(M')$, $I$ et $J$ les milieux respectifs de $[MM']$ et $[M'M''].$
On a : $$\left\lbrace\begin{array}{lcl} \overrightarrow{MM'}&=&2\overrightarrow{IM'}\\ \overrightarrow{M'M''}&=&2\overrightarrow{M'J'} \end{array}\right.\;,$$
d'où par addition membre à membre de ces deux égalités (relation de CHASLES) : $\overrightarrow{MM''}=2\overrightarrow{IJ}.$
On en déduit que $M''=t_{\overrightarrow{u}}(M)$ avec $\overrightarrow{u}=\overrightarrow{ij}.$
2) Cas où les axes $\Delta_{1}$ et $\Delta_{2}$ sont sécants
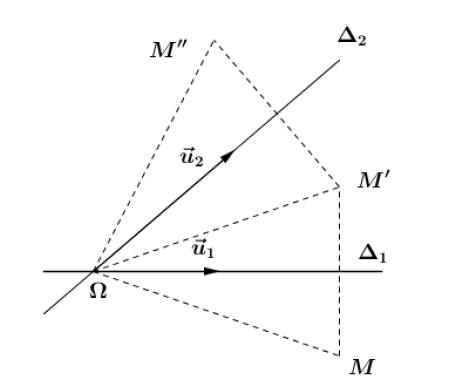
Théorème :
Soit $S_{\Delta_{1}}$ et $S_{\Delta_{2}}$ deux réflexions d'axes respectifs $\Delta_{1}$ et $\Delta_{2}$ sécants en $\Omega$ et de vecteurs directeurs respectifs $\overrightarrow{u_{1}}$ et $\overrightarrow{u_{2}}.$
La composée $S_{\Delta_{1}}\circ S_{\Delta_{2}}$ est alors la rotation de centre $\Omega$ et d'angle $2(\overrightarrow{u_{2}}\;,\ \overrightarrow{u_{1}}).$
Démonstration :
Soit $M'=S_{\Delta_{2}}(M)$ et $M''=S_{\Delta_{1}}(M').$
$\Omega$ étant à la fois sur $\Delta_{1}$ et $\Delta_{2}$, on a :
$S_{\Delta_{1}}\circ S_{\Delta_{2}}(\Omega)=S_{\Delta_{1}}(\Omega)=\Omega\quad (1)$
D'autre part, $S_{\Delta_{1}}$ et $S_{\Delta_{2}}$ étant des isométries, on a :
$\Omega M'=\Omega M\left(\text{ par }S_{\Delta_{2}}\right)$ et $\Omega M'=\Omega M''\left(\text{ par }S_{\Delta_{1}}\right)$, d'où : $\Omega M=\Omega M''\quad (2)$
Par ailleurs, $\left(\overrightarrow{\Omega M}\;,\ \overrightarrow{\Omega M''}\right)=\left(\overrightarrow{\Omega M}\;,\ \overrightarrow{u_{2}}\right)+\left(\overrightarrow{u_{2}}\;,\ \overrightarrow{u_{1}}\right)+\left(\overrightarrow{u_{1}}\;,\ \overrightarrow{\Omega M''}\right).$
Une réflexion étant un antidéplacement :
$\left(\overrightarrow{\Omega M}\;,\ \overrightarrow{u_{2}}\right)=-\left(\overrightarrow{\Omega M'}\;,\ \overrightarrow{u_{2}}\right)$ et $\left(\overrightarrow{u_{1}}\;,\ \overrightarrow{\Omega M''}\right)=-\left(\overrightarrow{u_{1}}\;,\ \overrightarrow{\Omega M'}\right).$
Donc , $\left(\overrightarrow{\Omega M}\;,\ \overrightarrow{\Omega M''}\right)=-\left(\overrightarrow{\Omega M'}\;,\ \overrightarrow{u_{2}}\right)+\left(\overrightarrow{u_{2}}\;,\ \overrightarrow{u_{1}}\right)-\left(\overrightarrow{u_{1}}\;,\ \overrightarrow{\Omega M'}\right)$, soit $$\left(\overrightarrow{\Omega M}\;,\ \overrightarrow{\Omega M''}\right)=2\left(\overrightarrow{u_{2}}\;,\ \overrightarrow{u_{1}}\right)\quad (3)$$
d'après la relation de Chasles sur les angles orientés.
Il résulte des relations $(1)$, $(2)$ et $(3)$ que $S_{\Delta_{1}}\circ S_{\Delta_{2}}$ est la rotation de centre $\Omega$ et d'angle $2\left(\overrightarrow{u_{2}}\;,\ \overrightarrow{u_{1}}\right).$
Remarques :
$\bullet$ L'angle $2\left(\overrightarrow{u_{2}}\;,\ \overrightarrow{u_{1}}\right)$ dépend uniquement des droites $\Delta_{1}$ et $\Delta_{2}$ et non des vecteurs directeurs $\overrightarrow{u_{1}}$ et $\overrightarrow{u_{2}}$ choisis sur cette droites.
Si par exemple on remplace $\overrightarrow{u_{2}}$ par $-\overrightarrow{u_{2}}$, on a :
$2\left(-\overrightarrow{u_{2}}\;,\ \overrightarrow{u_{1}}\right)=2\left(-\overrightarrow{u_{2}}\;,\ \overrightarrow{u_{2}}\right)+2\left(\overrightarrow{u_{2}}\;,\ \overrightarrow{u_{1}}\right)=2\left(\overrightarrow{u_{2}}\;,\ \overrightarrow{u_{1}}\right)[2\pi]$ car $$\left(-\overrightarrow{u_{2}}\;,\ \overrightarrow{u_{2}}\right)=\pi[2\pi]$$
$\bullet$ $S_{\Delta_{1}}$ et $S_{\Delta_{2}}$ ne commutent pas en général car $S_{\Delta_{1}}\circ S_{\Delta_{2}}$ est une rotation d'angle $2\left(\overrightarrow{u_{2}}\;,\ \overrightarrow{u_{1}}\right)$ tandis que $S_{\Delta_{2}}\circ S_{\Delta_{1}}$ est une rotation d'angle $2\left(\overrightarrow{u_{1}}\;,\ \overrightarrow{u_{2}}\right).$
Elles ne commutent que lorsque $\Delta_{1}\perp\Delta_{2}$ auquel cas :
$S_{\Delta_{2}}\circ S_{\Delta_{1}}=S_{\Delta_{1}}\circ S_{\Delta_{2}}=S_{\Omega}$ (symétrie centrale de centre $\Omega).$
$\bullet$ Toute rotation peut être décomposée comme la composée de deux symétries axiales d'axes sécants au centre de cette rotation.
L'un de ces axes pouvant être choisi arbitrairement, il existe une infinité de manières de faire cette décomposition.
Exemple :
Soit $ABC$ un triangle équilatéral direct de centre de gravité $G$ :
On note $A'$, $B'$ et $C'$ les milieux respectifs de $[BC]$ ; $[CA]$ ; $[AB]$ :
Soit $C''=t_{\overrightarrow{A'A}}(C).$
En utilisant des décompositions judicieusement choisies, écrire sous la forme d'une seule transformation les composées suivantes :
$f_{1}=r_{A\;,\dfrac{\pi}{3}}\circ r_{B\;,\dfrac{\pi}{3}}$ ;
$f_{2}=r_{C\;,-\dfrac{\pi}{3}}\circ r_{A\;,\dfrac{\pi}{3}}$ ;
$f_{3}=t_{\overrightarrow{BC}}\circ r_{A'\;,\pi}.$
Solution :
$\bullet$ $(AA')$ et $(AB)$ se coupent en $A$ (évident) et $\left(\overrightarrow{AB}\;,\ \overrightarrow{AA'}\right)=\dfrac{\pi}{6}$, donc $$r_{A\;,\dfrac{\pi}{3}}=S_{(AA')}\circ S_{(AB)}$$
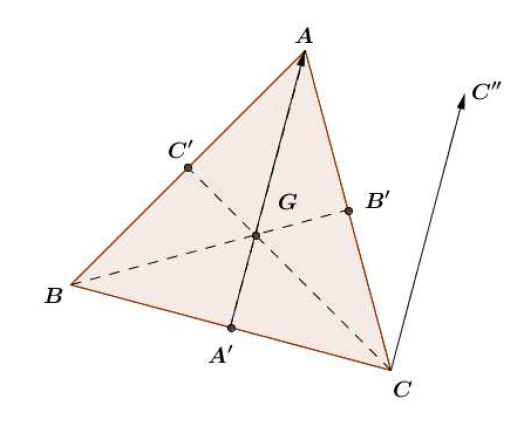
De la même manière, on voit que : $$r_{B\;,\dfrac{\pi}{3}}=S_{(AB)}\circ S_{(BB')}$$
Alors, d'après l'associativité de la composée des applications :
$f_{1}=r_{A\;,\dfrac{\pi}{3}}\circ r_{B\;,\dfrac{\pi}{3}}=S_{(AA')}\circ S_{(AB)}\circ S_{(AB)}\circ S_{(BB')}=S_{(AA')}\circ S_{(BB')}=r_{G\;,\dfrac{-4\pi}{3}}$
car $(AA')$ et $(BB')$ se coupent en $G$ et il n'est pas difficile de voir que :
$2\left(\overrightarrow{BB'}\;,\ \overrightarrow{AA'}\right)=2\left(\overrightarrow{GB'}\;,\ \overrightarrow{GA'}\right)=2\times\left(\dfrac{-2\pi}{3}\right)=-\dfrac{4\pi}{3}.$
$\bullet\ r_{C\;,-\dfrac{\pi}{3}}\circ r_{A\;,\dfrac{\pi}{3}}=S_{(CC'')}\circ S_{(AC)}\circ S_{(AC)}\circ S_{(AA')}=S_{(CC'')}\circ S_{(AA')}=t_{\overrightarrow{BC}}$
car $(CC'')$ et $(AA')$ sont parallèles et $\overrightarrow{A'C}=\dfrac{1}{2}\overrightarrow{BC}.$
$\bullet\ f_{3}=t_{\overrightarrow{BC}}\circ r_{A'\;,\pi}=S_{(CC'')}\circ S_{(AA')}\circ S_{(AA')}\circ S_{(BC)}=S_{(CC'')}\circ S_{(BC)}=r_{C\;,\pi}=S_{C}$.
V. Isométries du plan fixant un point
Théorème :
Soit $f$ une isométrie et $\Omega$ un point du plan.
L'isométrie $f$ se décompose d'une manière unique sous la forme $f=t\circ g$, où $t$ désigne une translation et $g$ désigne une isométrie laissant $\Omega$ fixe.
Démonstration :
Soit $f=t\circ g$ une telle décomposition (en supposant qu'elle existe).
On doit avoir $\Omega'=f(\Omega)=(t\circ g)(\Omega)=t(\Omega).$
La translation $t$ ne peut donc être que la translation de vecteur $\overrightarrow{\Omega\Omega'}.$
De plus $f=t\circ g$ d'où $g=t^{-1}\circ f.$
Donc la décomposition $f=t\circ g$ est, si elle existe, unique.
Posons maintenant $t=t_{\overrightarrow{\Omega\Omega'}}$ et $g=t^{-1}\circ f$ $g$ est bien une isométrie comme la composée de deux isométries.
De plus, $g(\Omega)=\left(t^{-1}\circ f\right)(\Omega)=t^{-1}[f(\Omega)]=\Omega$ , donc $\Omega$ est bien un point fixe de $g.$
Finalement $t\circ g=t\circ\left(t^{-1}\circ f\right)=\left(t\circ t^{-1}\right)\circ f=f.$
Ceci montre l'existence de la décomposition citée dans le théorème.
Le théorème montre qu'une isométrie quelconque peut toujours être obtenue, et ce d'une infinité de manières (le choix de $\Omega$ est arbitraire), comme composée d'une isométrie laissant un point fixe et d'une translation.
Théorème :
1) Une isométrie fixant trois points $A$, $B$ et $C$ non alignés est l'identité.
2) Une isométrie distincte de l'identité fixant au moins deux points distincts $A$ et $B$ est la symétrie axiale d'axe $(AB).$
3) Une isométrie ne fixant que le point $A$ est une rotation de centre $A$ et d'angle non nul.
Démonstration :
Soit $f$ une isométrie.
1) Supposons que $f$ fixe trois points $A$, $B$ et $C$ non alignés.
Soit $M$ un point quelconque du plan et soit $M'=f(M)$ :
$f$ conservant les distances, on doit avoir $AM=AM'$, $BM=BM'$ et $CM=CM'.$
Si $M\neq M'$, les trois points $A$, $B$ et $C$ devraient être tous les trois sur la médiatrice de $[MM']$, ce qui est impossible puisqu'ils ne sont pas alignés.
On a donc $M=M'$ et tous les points du plan sont donc fixes : $f=Id.$
2) Supposons que $f$ fixe deux points $A$ et $B$ distincts et que $f$ ne soit pas l'identité.
Soit $C$ un point qui n'est pas sur la droite $(AB).$
D'après 1), $f(C)=C'\neq C$, sinon on aurait $f=Id.$
$f$ conservant les distances, on doit avoir $AC=AC'$ et $BC=BC'.$
Donc la droite $(AB)$ est la médiatrice de $[CC'].$
Soit $g=S_{(AB)}\circ f.$
On a $g(A)=A$, $g(B)=B$ et $g(C)=S_{(AB)}[f(C)]=S_{(AB)}[C']=C.$
Alors $g$ a trois points invariants non alignés, $A$, $B$ et $C$ et d'après 1) : $g=Id.$
D'où (en composant à gauche par $S_{(AB)}$ : $f=S_{(AB)}\circ\;Id=S_{(AB)}.$
3) Supposons que $f$ ne fixe que le point $A.$
Soit $B$ un point distinct de $A$ et $B'=f(B).$
$f$ conservant les distances, on a $AB=AB'$, donc $A$ appartient à la médiatrice $\Delta$ de $[BB'].$
Soit $g=S_{\Delta}\circ f.$
On a : $g(A)=S_{\Delta}[f(A)]=S_{\Delta}(A)=A$ et $g(B)=S_{\Delta}[f(B)]=S_{\Delta}(B')=B.$
D'après les parties 1) et 2) ci-dessus, $g$ est soit l'identité, soit $S_{(AB)}.$
Si $g$ était l'identité, on aurait $f=S_{\Delta}$ ce qui est absurde, car $f$ n'a que $A$ comme point invariant par hypothèse.
Donc $g=S_{\Delta}\circ f=S_{(AB)}$, d'où (toujours en composant à gauche par $S_{(AB)})$ :
$f=S_{\Delta}\circ S_{(AB)}.$
Les droites $\Delta$ et $(AB)$ étant sécantes en $A$ (si elles étaient parallèles, elles seraient confondues, car elles ont en commun le point $A$, et $B$ appartiendrait à la médiatrice de $[BB']$, ce qui est absurde), $f$ est une rotation de centre $A.$
VI. Déplacements et antidéplacements
1) Déplacements du plan
Soit $f$ un déplacement du plan.
$-\ \ $ Si $f$ fixe un point, ce ne peut être que l'identité ou une rotation.
$-\ \ $ Si $f$ ne fixe aucun point, alors $f=t\circ g$ avec $g$ fixant un point.
$g=t^{-1}\circ f$ est un déplacement fixant un point.
C'est donc l'identité ou une rotation.
a) Si $g$ est l'identité, $f=t\circ\;Id=t.$
b) Si $g$ est une rotation $r$ : $f=t\circ r.$
Décomposons $t$ et $r$ en produit de réflexions bien choisies.
$t=s_{1}\circ s_{2}$ et $r=s_{2}\circ s_{3}$ :
Alors $t\circ r=s_{1}\circ s_{2}\circ s_{2}\circ s_{3}=s_{1}\circ s_{3}$ est donc une translation ou une rotation.
Théorème :
Les déplacements du plan sont les translations et les rotations
2) Antidéplacements du plan
Soit $f$ un antidéplacement du plan.
-Si $f$ fixe un point, ce ne peut être qu'une réflexion
-Si $f$ ne fixe aucun point, alors $f=t\circ g$ avec $g$ fixant un point.
$g=t^{-1}\circ f$ est un antidéplacement fixant un point.
C'est donc une réflexion $s.$
Alors : $f=t\circ s$
Théorème :
Les antidéplacements du plan sont les réflexions et les composées $t\circ s$ ou $t$ est une translation et $s$ une réflexion.
Définition :
Une symétrie glissée est la composition d'une translation de vecteur $\overrightarrow{u}$ et d'une réflexion d'axe $\Delta$ dont $\overrightarrow{u}$ est un vecteur directeur.
On la note $S_{\Delta\;,\overrightarrow{u}}.$
Théorème :
La composée d'une translation et d'une réflexion est une réflexion ou une symétrie glissée.
Démonstration :
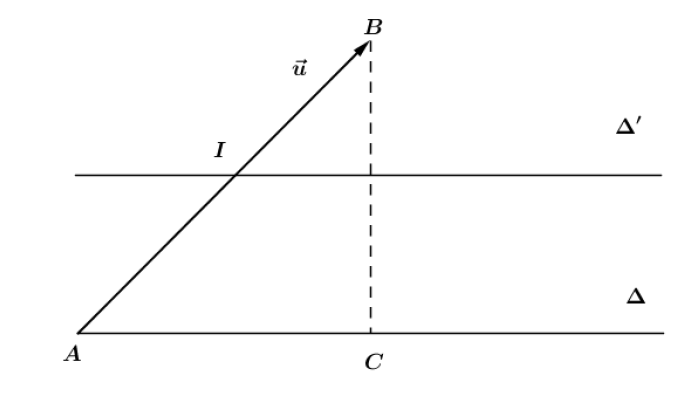
Soit $f=t_{\overrightarrow{u}}\circ S_{\Delta}.$
Soit $A$ un point de $\Delta$ et $B$ le point tel que $\overrightarrow{AB}=\overrightarrow{u}.$
Soit $C$ le projeté orthogonal de $B$ sur $\Delta$ et $\Delta'$ la parallèle à $\Delta$ passant par le milieu $I$ de $[AB].$
On a : $t_{\overrightarrow{u}}=t_{\overrightarrow{AC}+\overrightarrow{CB}}=t_{\overrightarrow{AC}}\circ t_{\overrightarrow{CB}}$ et $t_{\overrightarrow{CB}}=S_{\Delta'}\circ S_{\Delta}$, d'où :
$f=t_{\overrightarrow{AC}}\circ S_{\Delta'}\circ S_{\Delta}\circ S_{\Delta}=t_{\overrightarrow{AC}}\circ S_{\Delta'}.$
$-\ \ $ Si $\overrightarrow{AC}=\overrightarrow{0}$, alors $f=S_{\Delta'}.$
$-\ \ $ Si $\overrightarrow{AC}\neq\overrightarrow{0}$, alors $f=t_{\overrightarrow{AC}}\circ S_{\Delta'}$ avec $\overrightarrow{AC}$ vecteur directeur de $\Delta'.$
Donc $f$ est la symétrie glissée $S_{\Delta'\overrightarrow{AC}}.$
Théorème :
La symétrie glissée $S_{\Delta\;,\overrightarrow{u}}$ est une composée commutative, c'est-à-dire que l'on a : $S_{\Delta\;,\overrightarrow{u}}=t_{\overrightarrow{u}}\circ S_{\Delta}=S_{\Delta}\circ t_{\overrightarrow{u}}.$
Démonstration :
$t_{\overrightarrow{u}}\circ S_{\Delta}\circ t_{-\overrightarrow{u}}$ est un antidéplacement comme composée de trois antidéplacements.
Si $M\in\Delta$, posons $M_{1}=t_{-\overrightarrow{u}}(M).$
On a donc $\overrightarrow{MM_{1}}=-\overrightarrow{u}.$
$\overrightarrow{u}$ étant vecteur directeur de $\Delta$, $M_{1}\in\Delta.$
D'où $\left(t_{\overrightarrow{u}}\circ S_{\Delta}\circ t_{-\overrightarrow{u}}\right)(M)=t_{\overrightarrow{u}}\circ S_{\Delta}(M_{1})=t_{\overrightarrow{u}}(M_{1})=M$ car $\overrightarrow{M_{1}M}=-\overrightarrow{u}.$
$t_{\overrightarrow{u}}\circ S_{\Delta}\circ t_{-\overrightarrow{u}}$ est donc un antidéplacement fixant tout point de $\Delta$ et il en résulte
que :
$t_{\overrightarrow{u}}\circ S_{\Delta}\circ t_{-\overrightarrow{u}}=S_{\Delta}.$
Par conséquent : $t_{\overrightarrow{u}}\circ S_{\Delta}=S_{\Delta}\circ t_{-\overrightarrow{u}}.$
Remarque :
On en déduit que si $f=S_{\Delta\;,\overrightarrow{u}}$ est une symétrie glissée, alors on a $$f\circ f=t_{2\overrightarrow{u}}$$
En effet, $f\circ f=\left(t_{\overrightarrow{u}}\circ S_{\Delta}\right)\circ\left(S_{\Delta}\circ t_{\overrightarrow{u}}\right)=t_{\overrightarrow{u}}\circ t_{\overrightarrow{u}}=t_{2\overrightarrow{u}}.$
D'autre part, $f=t_{\overrightarrow{u}}\circ S_{\Delta}\Rightarrow S_{\Delta}=t_{-\overrightarrow{u}}\circ f.$
Ainsi la connaissance de $f$ permet d'obtenir $\overrightarrow{u}$ et $\Delta.$
Théorème :
Les antidéplacements du plan sont les réflexions et les symétries glissées.
Auteur:
Ka, Faye & Mbengue

Commentaires
Anonyme (non vérifié)
jeu, 07/08/2021 - 17:16
Permalien
<html></html>
Ajouter un commentaire