Vous êtes ici

Multiplication des nombres décimaux arithmétiques 6e

Classe:

Sixième

I. Vocabulaire

Activité 1 :

Pour organiser une fête ; une

$ASC$ loue

$5$ bâches à

$2\,500\;F$ l'unité.

Calculer le montant à payer de deux façons différentes.

Solution

$-\$ Première façon : le montant à payer est de

$2\,500\;F+2\,500\;F+2\,500\;F+2\,500\;F+2\,500\;F=12\,500\;F$

$-\$ Deuxième façon : le montant à payer est de

$2\,500\;F\times 5=12\,500\;F$

Donc, l'

$ASC$ doit payer

$12\,500\;F$ pour la location des

$5$ bâches.

Activité 2 :

Moussa achète à la boutique

$2.5\;Kg$ de sucre en raison de

$650\;F$ le

$Kg.$

Quel est le prix d'achat du sucre ?

Solution

Le prix d'achat du sucre est de :

$625\;F\times 2.5=1\,625\;F$

Le nombre

$1\,625$ est le produit de

$2.5\$ et

$\ 650.$

Les nombres

$2.5\$ et

$\ 650$ sont les facteurs de l'opération (produit).

L'opération effectuée est la multiplication.

Le signe de la multiplication est

$"\times"$

La multiplication dans

$\mathfrak{D}$ est l'opération qui à deux décimaux

$a$ et

$b$ associe le produit noté

$a\times b\;\text{ ou }\;a.b\;\text{ ou encore }\;ab$

$a\$ et

$\ b$ sont les facteurs et le produit est

$a\times b$

Attention :

Il faut utiliser les écritures

$ab$ ou

$a.b$ lorsque les nombres sont inconnus ou variable.

Exemples :

$a\times x=a.x=ax\;;\quad a\times a=a.a=aa=a^{2}$

Par contre :

$3\times 7=21\;;\quad 3.7=3,7 \;;\quad 37=\text{trente-sept}$

II. Propriétés

II.1 Commutativité

Activité :

Calculer de deux façons différentes les opérations suivantes :

$4\times 25\;;\quad 42\times 0.9$

Solution

On a :

$4\times 25=100\$ et

$\ 25\times 4=100$

$42\times 0.9=37.8\$ et

$\ 0.9\times 42=37.8$

Énoncé :

Pour calculer un produit ;on peut changer l'ordre des deux facteurs sans modifier le résultat ; on dit que la multiplication est commutative.

II.2 Associativité

Activité

Calculer de deux façons différentes les opérations suivantes :

$50\times 8\times 3.4\;;\quad 15\times 5\times 10$

Solution

On a :

$50\times 8\times 3.4=1\,360$

$50\times 8\times 3.4=400\times 3.4=1\,360$

$15\times 5\times 10=750$

$15\times 5\times 10=75\times 10=750$

Énoncé :

Pour multiplier trois facteurs;on peut multiplier deux facteurs et le produit est multiplié par le

$3^{e}$ facteur ; on dit que la multiplication est associative.

II.3 Rôle de zéro et de un

Énoncé :

Tout nombre multiplié par zéro a un produit nul; on dit que zéro est l'élément absorbant de la multiplication.

Exemple :

$17\times 0=0$

Énoncé :

Tout nombre multiplié par un a un produit égal à ce nombre lui-même ; on dit que un est l'élément neutre de la multiplication.

Exemple :

$12.5\times 1=12.5$

II.4 Distributivité

Activité 1

Complète puis compare :

$(5\times 7.5)+(5\times 8.5)\;;\quad 5\times(7.5+8.5)$

Solution

Complétons puis comparons

$\begin{array}{rcl}(5\times 7.5)+(5\times 8.5)&=&37.5+42.5\\\\&=&80\end{array}$

$\begin{array}{rcl}5\times(7.5+8.5)&=&5\times 16\\\\&=&80\end{array}$

D'où,

$(5\times 7.5)+(5\times 8.5)=5\times(7.5+8.5)$

Activité 2

Soit

$ABCD$ un rectangle avec

$a=3\;cm\;,\ b=5\;cm\$ et

$\ c=2\;cm.$

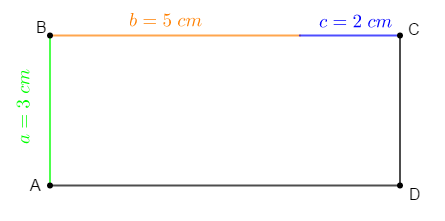
Pour calculer l'aire de

$ABCD$ :

Moussa propose :

$3\times(5+2)$

Abdou propose :

$(3\times 5)+(3\times 2)$

Calcul puis compare

Solution

Calculons puis comparons

Avec la proposition de Moussa, on a :

$\begin{array}{rcl}3\times(5+2)&=&3\times 7\\\\&=&21\end{array}$

Avec la proposition de Moussa, on a :

$\begin{array}{rcl}(3\times 5)+(3\times 2)&=&15+6\\\\&=&21\end{array}$

Donc, l'aire de

$ABCD$ est égale à

$21\;cm^{2}$

Par suite,

$3\times(5+2)=(3\times 5)+(3\times 2)$

Ainsi, Moussa et Abdou obtiennent le même résultat.

Cas général :

Pour multiplier une somme par un nombre ; on peut multiplier chaque terme de la somme par ce nombre et additionner les produits obtenus :

$a\times(b+c)=(a\times b)=a\times b+a\times c$

Pour multiplier une différence par un nombre ; on peut multiplier chaque terme de la différence par ce nombre et soustraire les produits obtenus :

$a\times(b-c)=(a\times b)-(a\times c)=a\times b-a\times c$

On dit que la multiplication est distributive par rapport à l'addition et à la soustraction.

Exercices d'application

Donner une autre écriture puis calculer

$a=(5.8-4.2)\times 2.5$

$b=3\times 100+3\times 2.5$

$c=5\times(25+7.8)$

$d=375\times 2-12.5\times 2$

Solution

Donnons une autre écriture puis calculons

On a :

$a=(5.8-4.2)\times 2.5=5.8\times 2.5-4.2\times 2.5$

Donc,

$\begin{array}{rcl} a&=&5.8\times 2.5-4.2\times 2.5\\\\&=&14.5-10.5\\\\&=&4\end{array}$

Ainsi,

$\boxed{a=4}$

Soit :

$b=3\times 100+3\times 2.5=3\times(100+2.5)$

Par suite,

$\begin{array}{rcl} b&=&3\times(100+2.5)\\\\&=&3\times 102.5\\\\&=&307.5\end{array}$

D'où,

$\boxed{b=307.5}$

On a :

$c=5\times(25+7.8)=5\times 25+5\times 7.8$

Donc,

$\begin{array}{rcl} c&=&5\times 25+5\times 7.8\\\\&=&125+39\\\\&=&164\end{array}$

D'où,

$\boxed{c=164}$

Soit :

$d=375\times 2-12.5\times 2=(375-12.5)\times 2$

Alors,

$\begin{array}{rcl} d&=&(375-12.5)\times 2\\\\&=&362.5\times 2\\\\&=&725\end{array}$

Ainsi,

$\boxed{d=725}$

III. Puissances

III.1 Carré d'un nombre

Le produit de

$a$ par

$a$ noté

$a^{2}$ est une puissance de deux

On lit :

$a$ au carré ou

$a$ à la puissance deux ou

$a$ exposant deux

III.2 Cube d'un nombre

Le produit de

$a^{3}$ est une puissance de trois.

On lit :

$a$ au cube ou

$a$ à la puissance trois ou

$a$ exposant trois.

Exercice d'application

Soit un bassin cubique dont les arêtes mesurent

$5\;m$

Calculer sa surface de base, puis son volume

Solution

Comme le bassin a la forme d'un cube donc, sa base est un carré de côté

$a=5\;m$

Par suite,

$\begin{array}{rcl} \text{Surface de base}&=&a^{2}\\\\&=&5^{2}\\\\&=&25\end{array}$

D'où,

$\boxed{\text{Surface de base}=25\;m^{2}}$

Le volume de ce bassin est donné par :

$\begin{array}{rcl} \text{Volume}&=&a^{3}\\\\&=&5^{3}\\\\&=&125\end{array}$

Ainsi,

$\boxed{\text{Volume du bassin}=125\;m^{3}}$

Commentaires

Anonyme (non vérifié)

lun, 03/17/2025 - 23:11

Permalien

J’ai bien compris la leçon à

J’ai bien compris la leçon à base des exercices d’application

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Multiplication des nombres décimaux arithmétiques 6e

Formulaire de recherche

I. Vocabulaire

Activité 1 :

Solution

Activité 2 :

Solution

Attention :

Exemples :

II. Propriétés

II.1 Commutativité

Activité :

Solution

Énoncé :

II.2 Associativité

Activité

Solution

Énoncé :

II.3 Rôle de zéro et de un

Énoncé :

Exemple :

Énoncé :

Exemple :

II.4 Distributivité

Activité 1

Solution

Activité 2

Solution

Cas général :

Exercices d'application

Solution

III. Puissances

III.1 Carré d'un nombre

III.2 Cube d'un nombre

Exercice d'application

Solution

Commentaires

J’ai bien compris la leçon à

Ajouter un commentaire

Plain text