Partage d'un segment en trois parties égales - 3e
Classe:
Troisième
Nous allons proposer une manière de partager ou de diviser un segment en trois parties égales, en appliquant les propriétés suivantes :
I. Application du théorème de Thalès
On trace un segment $[AB]$ de longueur $a$ (non divisible par 3) à diviser en trois parties de même longueur.
A partir de l'une de ses extrémités, on trace une demi-droite.
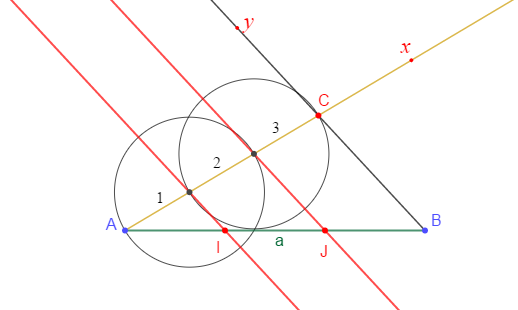
Traçons la demi-droite $[Ax)$ puis avec le compas, reportons trois segments de même longueur sur cette demi-droite et marquons le point $C$ extrémité du troisième segment.
Ensuite, traçons la demi-droite $[By)$ passant par le point $C.$
Enfin, les parallèles à $[By)$ découpent le segment $[AB]$ en trois parties égales :
$$AI=IJ=JB$$
II. Application du point de rencontre des médianes
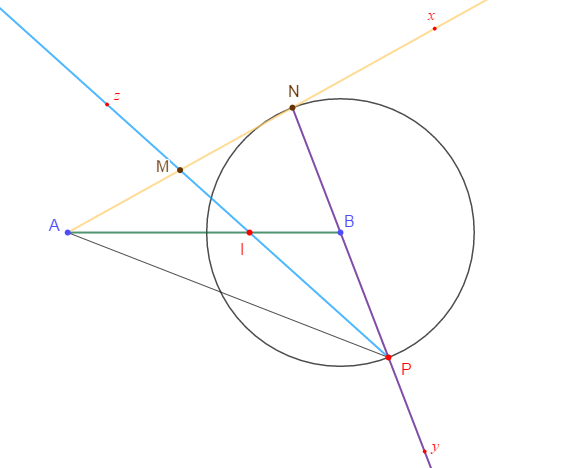
Sur une demi-droite d'origine $A$, on marque deux points $M\ $ et $\ N$ tels que :
$$AM=MN$$
Sur une demi-droite d'origine $N$ passant par $B$, on marque le point $P$ tel que :
$$NB=BP$$
La demi-droite d'origine $P$ passant par $M$ coupe $[AB]$ en $I.$
Remarquons que $AB\ $ et $\ MP$ sont deux médianes du triangle $ANP.$
Elles se coupent donc aux deux tiers à partir de leurs sommets.
$$AI=\dfrac{2}{3}AB$$

Commentaires
Anonyme (non vérifié)
jeu, 08/06/2020 - 03:25
Permalien
Excellent
Anonyme (non vérifié)
mer, 07/28/2021 - 01:14
Permalien
tres bien
Anonyme (non vérifié)
lun, 08/01/2022 - 19:59
Permalien
appr
Ajouter un commentaire