Vous êtes ici

Probabilités - T S

Classe:

Terminale

Exemple :

Une urne contient une boule rouge, une boule noire et une boule verte. On tire successivement deux boules de l'urne en remettant la boule tirée dans l'urne après chaque tirage.

I Vocabulaire

I.1 Univers

L'ensemble des résultats possibles est appelé univers

$\Omega.$

Dans l'exemple on a :

$\Omega=\{(R\;,\ R)\;,\ (R\;,\ N)\;,\ (R\;,\ V)\;,\ (V\;,\ V)\;,\ (V\;,\ R)\;,\ (V\;,\ N)\;,\ (N\;,\ N)\;,\ (N\;,\ R)\;,\ (N\;,\ V)\}$

$\Omega$ est l'ensemble des

$2-$ listes (couples) pris dans un ensemble à trois

$(3)$ éléments

$(1N\;,\ 1R\;,\ 1V).$

Donc

$Card\;\Omega=3^{2}=9$

I.2 Événement

Toute partie

$E\subset\Omega$ est appelée événement.

Exemple :

$A_{1}=\{(R\;,\ R)\}$ = "tirer

$2$ boules rouges"

$A=\{(R\;,\ R)\;,\ (V\;,\ V)\;,\ (N\;,\ N)\}$ = "tirer

$2$ boules de même couleur"

$B=\{(R\;,\ N)\;,\ (R\;,\ V)\;,\ (V\;,\ R)\;,\ (V\;,\ N)\;,\ (N\;,\ R)\;,\ (N\;,\ V)\}$ = "tirer

$2$ boules de couleurs différentes"

$C=\{(R\;,\ V)\;,\ (V\;,\ V)\;,\ (V\;,\ R)\;,\ (V\;,\ N)\;,\ (N\;,\ V)\}$ = "tirer au moins une boule verte"

$D=\{(R\;,\ R)\;,\ (V\;,\ V)\}$ = "tirer

$2$ boules rouges ou

$2$ boules vertes"

On dira qu'un événement

$E$ est réalisé si le résultat de l'expérience appartient à

$E.$

$\centerdot\ \$ Événement certain : l'univers

$\Omega$ est appelé événement certain.

$\centerdot\ \$ Événement impossible : l'ensemble vide

$\emptyset$ est appelé événement impossible.

Dans l'exemple, l'événement "tirer

boules jaunes" est

$\emptyset$ . C'est l'événement impossible. Il ne se réalise jamais.

$\centerdot\ \$ Événement élémentaire : tout singleton de

$\Omega$ est appelé événement élémentaire.

Exemple :

$A_{1}=\{(R\;,\ R)\}\$ et

$\ B_{1}=\{(R\;,\ V)\}$ sont des événements élémentaires.

Remarque :

un événement quelconque est une réunion d'événements élémentaires.

$\centerdot\ \$ Événement

$E\$ ou

$\ F$ : l'événement

$E\$ ou

$\ F$ noté

$E\cup F$ est réalisé si le résultat de l'expérience appartient à

$E$ ou appartient à

$F.$

$A\cup C=\{(R\;,\ R)\;,\ (V\;,\ V)\;,\ (N\;,\ N)\;,\ (R\;,\ V)\;,\ (V\;,\ R)\;,\ (V\;,\ N)\;,\ (N\;,\ V)\}$ = "tirer au moins une boule verte ou

$2$ boules de même couleur"

$\centerdot\ \$ Événement

$E\$ et

$\ F$ : l'événement

$E\$ et

$\ F$ noté

$E\cap F$ est réalisé si le résultat de l'expérience appartient à

$E$ et appartient à

$F.$

$A\cap C=\{(V\;,\ V)\}$

$\centerdot\ \$ Événements incompatibles : deux événements

$E\$ et

$\ F$ sont dits incompatibles si

$E\cap F=\emptyset$ (c'est-à-dire qu'on ne peut réaliser

$E\$ et

$\ F$ en même temps).

Exemple :

$A\$ et

$\ B$ ou encore

$B\$ et

$\ D$ sont incompatibles.

$\centerdot\ \$ Événements contraires : deux événements

$E\$ et

$\ F$ sont dits contraires s'ils sont incompatibles et vérifient

$E\cup F=\Omega.$

L'événement contraire de

$E$ est noté

$\overline{E}.$

Exemple :

$A\$ et

$\ B$ sont contraires

$B\$ et

$\ D$ sont incompatibles mais ne sont pas contraires.

$\centerdot\ \$ Partition de l'univers

$\Omega$ :

$E_{1}\;,\ E_{2}\;,\ \ldots\;,\ E_{n}$ forment une partition de l'univers

$\Omega$ si

$\left\lbrace\begin{array}{rcr} E_{i}\cap E_{j} &=& \emptyset\quad\text{ si }\;i\neq j \\ \\ E_{1}\cup E_{2}\cup\ldots\cup E_{n} &=& \bigcup_{i=1}^{n} E_{i}\;=\;\Omega\end{array}\right.$

Remarque :

deux événements contraires constituent une partition de l'univers

$\Omega.$

II Définition et propriétés

Dans l'exemple nous avons

$Card\;\Omega=9$

Soit

$A_{1}=\{(R\;,\ R)\}$ alors, l'événement

$A_{1}$ a une chance sur

$9$ d'être réalisé.

On dira que la probabilité de

$A_{1}$ notée

$p(A_{1})$ est

$\dfrac{1}{9}.$

$p(A_{1})=\dfrac{1}{9}$

L'événement

$A$ a

$3$ chance sur

$9$ d'être réalisé

$p(A)=\dfrac{3}{9}=\dfrac{1}{3}$

L'événement

$B$ a

$6$ chance sur

$9$ d'être réalisé

$p(B)=\dfrac{6}{9}=\dfrac{2}{3}$

II.1 Définition

on appelle probabilité l'application notée

$\begin{eqnarray} p\ :\ \mathcal{P}(\Omega) &\longrightarrow & [0\;,\ 1] \nonumber \\ A & \longrightarrow & p(A) \nonumber \end{eqnarray}$

qui vérifie

$p(\Omega)=1$

ii)

$\forall\;E\;\text{ et }\;F\;,\ p(E\cup F)=p(E)+p(F)-p(E\cap F)$

avec si

$E=\{e_{i}\;;\ i\in I\}$ , alors

$p(E)=\sum_{i\in I}p(\{e_{i}\})$

II.2 Propriétés

$\centerdot\ \ p(\emptyset)=0$

$\centerdot\ \$ si

$E\cap F=\emptyset$ alors,

$p(E\cup F)=p(E)+p(F)$

$\centerdot\ \ p(E)+p(\overline{E})=1$

$\centerdot\ \$ si

$E_{1}\;,\ E_{2}\;,\ \ldots\;,\ E_{n}$ forment une partition de

$\Omega$ alors,

$\sum_{i=1}^{n}p(E_{i})=1$

$\centerdot\ \$ soit

$\Omega=\{\omega_{1}\;,\ \omega_{2}\;,\ \omega_{3}\;,\ \ldots\;,\ \omega_{n}\}$ avec

$\omega_{i}$ événement élémentaire.

Si les événements élémentaires ont la même probabilité, on dira qu'il y a équiprobabilité et dans ce cas ;

$E$ quelconque

$p(E)=\dfrac{Card\;E}{Card\;\Omega}$

II.3 Événements indépendants

Deux événements

$E\$ et

$\ F$ sont dits indépendants si, et seulement si,

$p(E\cap F)=p(E)\times p(F)$

Exercice d'application

Dans un jeu de

$32$ cartes, on tire simultanément

$4$ cartes.

1) Calculer la probabilité de tirer

a) exactement un roi

b) un roi de cœur

c) exactement un roi et un cœur

d) exactement un roi ou un cœur

2) Les événements de a) et de b) sont-ils indépendants ?

Résolution

L'univers

$\Omega$ est l'ensemble des partes à

$4$ éléments pris dans

$32$ cartes.

$Card\;\Omega=C_{32}^{4}=35\,960$

a) Soit

$A$ l'événement "tirer exactement un roi"

$p(A)=\dfrac{C_{4}^{1}\times C_{28}^{3}}{C_{32}^{4}}=0.36$

b) Soit

$B$ l'événement "tirer un roi de cœur"

$p(B)=\dfrac{C_{1}^{1}\times C_{31}^{3}}{C_{32}^{4}}=0.12$

c) Soit

$C$ l'événement "tirer exactement un roi et un cœur"

$p(C)=\dfrac{C_{1}^{1}\times C_{24}^{3}+C_{3}^{1}\times C_{7}^{1}\times C_{21}^{2}}{C_{32}^{4}}=0.17$

d) Soit

$D$ l'événement "tirer exactement un roi ou un cœur"

On a :

$D=A\cup E$ avec

$E$ l'événement "tirer exactement un cœur"

donc,

$p(D)=p(A\cup E)=p(A)+p(E)-p(A\cap E)$ or,

$\ A\cap E=C$

On a

$p(E)=\dfrac{C_{8}^{1}\times C_{24}^{3}}{C_{32}^{4}}=0.45$

ainsi,

$p(D)=0.36+0.45-0.17=0.64$

$A\$ et

$\ B$ indépendants

$\Leftrightarrow\ p(A\cap B)=p(A)\times p(B)$

On a

$p(A\cap B)=\dfrac{C_{1}^{1}\times C_{28}^{3}}{C_{32}^{4}}=0.09$

$p(A)\times p(B)=0.36\times 0.12=0.04$

On voit bien que

$p(A\cap B)\neq p(A)\times p(B)$

donc

$A\$ et

$\ B$ ne sont pas indépendants.

III Probabilités conditionnelles

Exemple :

Dans une entreprise on compte

$200$ hommes et

$80$ filles. Parmi les hommes on a

$20$ cadres et le reste des ouvriers. Parmi les filles,

$6$ cadres et le reste des ouvriers.

On choisit une personne au hasard.

Déterminer la probabilité pour que la personne choisie soit :

a) un ouvrier

b) un cadre

c) un homme ; une femme

d) un homme sachant que c'est un cadre

e) un cadre sachant que c'est un homme

f) un homme cadre

g) une femme sachant que c'est un cadre

h) un cadre sachant que c'est une femme

Résolution :

Soit le tableau suivant :

$\begin{array}{|c|c|c|c|}\hline & \text{Hommes }(H) & \text{Femmes }(F) & \text{Total} \\ \hline\text{Ouvrier }(O) & 180 & 74 & 254 \\ \hline\text{Cadre }(C) & 20 & 6 & 26 \\ \hline\text{Total} & 200 & 80 & 280 \\ \hline\end{array}$

a) Soit

$O$ l'événement "la personne choisie soit un ouvrier"

On a

$p(O)=\dfrac{C_{254}^{1}}{280}=\dfrac{254}{280}=\dfrac{127}{140}$

$C$ est l'événement "la personne choisie soit un cadre"

On a

$p(C)=\dfrac{C_{26}^{1}}{280}=\dfrac{26}{280}=\dfrac{13}{140}$

c) la personne choisie est un homme. Soit

$H$ cet événement.

On a

$p(H)=\dfrac{C_{200}^{1}}{280}=\dfrac{200}{280}=\dfrac{5}{7}$

Si la personne choisie est une femme, dans ce cas on aura

$p(F)=\dfrac{2}{7}$ avec

$F$ cet événement.

d) On choisit un homme sachant que c'est un cadre. Soit

$(H/C)$ cet événement.

On a

$p(H/C)\;\text{ ou }\;p_{_{C}}(H)=\dfrac{C_{20}^{1}}{26}=\dfrac{20}{26}=\dfrac{10}{13}$

e) Choisir un cadre sachant qu'il est un homme.

On a

$p_{_{H}}(C)=\dfrac{C_{20}^{1}}{200}=\dfrac{1}{10}$

f) Soit

$H\cap C$ l'événement "la personne choisie est un homme cadre".

On a

$p(H\cap C)=\dfrac{20}{280}=\dfrac{1}{14}$

g) La probabilité de l'événement "choisir une femme sachant que c'est un cadre" est donnée par :

$p_{_{C}}(F)=\dfrac{C_{6}^{1}}{26}=\dfrac{6}{26}=\dfrac{3}{13}$

h) Choisir un cadre sachant que c'est une femme.

La probabilité de cet événement est :

$p_{_{F}}(C)=\dfrac{C_{6}^{1}}{80}=\dfrac{6}{80}=\dfrac{3}{40}$

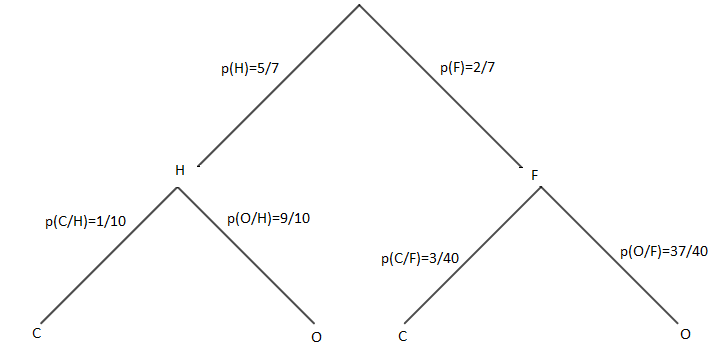
Arbre des probabilités

III.1 Définition

On appelle probabilité de

$B$ sachant

$A$ (qui est la probabilité pour que

$B$ soit réalisé sachant que

$A$ est réalisé) noté

$p_{_{A}}(B)\$ ou

$\ p(B/A).$

On a

$p_{_{A}}(B)\;\text{ ou }\;p(B/A)=\dfrac{p(A\cap B)}{p(A)}$

III.2 Propriétés

Soient

$A\$ et

$\ B$ deux événements quelconques, alors on a :

$\centerdot\ \ p_{_{B}}(A)=\dfrac{p(A\cap B)}{p(B)}$

$\centerdot\ \ p_{_{A}}(B)=\dfrac{p(A\cap B)}{p(A)}$

$\centerdot\ \ p(A\cap B)=p_{_{A}}(B)\times p(A)=p_{_{B}}(A)\times p(B)$

$\centerdot\ \ A\$ et

$\ B$ sont indépendants si

$p_{_{A}}(B)=p(B)$ ou encore si

$p_{_{B}}(A)=p(A)$

$\centerdot\ \$ Formule des probabilités totales ou Loi de Bayes

$E_{1}\;,\ E_{2}\;,\ \ldots\;,\ E_{n}$ forment une partition de

$\Omega\;;\ A$ un événement, alors on a :

$\begin{array}{rcl} p(A) &=& p(A\cap\Omega) \\ \\ &=& p\left[A\cap\left(E_{1}\cup E_{2}\cup\ldots\cup E_{n}\right)\right] \\ \\ &=& p(A\cap E_{1})+p(A\cap E_{2})+\ldots\ldots+p(A\cap E_{n}) \end{array}$

donc,

$p(A)=p(A\cap E_{1})+p(A\cap E_{2})+\ldots\ldots+p(A\cap E_{n})$

ce qui donne

$\boxed{p(A)=p(A/E_{1})\times p(E_{1})+p(A/E_{2})\times p(E_{2})+\ldots\ldots+p(A/E_{n})\times p(E_{n})}$

Cette dernière relation est appelée formule des probabilités totales.

Dans l'exemple précédent, nous pouvons donc écrire :

$\begin{array}{rcl} p(H) &=& p(H\cap O)+p(H\cap C) \\ \\ &=& p(H/O)\times p(O)+p(H/C)\times p(C) \end{array}$

$\begin{array}{rcl} p(C) &=& p(C\cap F)+p(C\cap H) \\ \\ &=& p(C/F)\times p(F)+p(C/H)\times p(H) \end{array}$

IV Schéma de Bernoulli

IV.1 Épreuve de Bernoulli

Une épreuve de Bernoulli est une expérience aléatoire qui n'a que deux issues : le succès (S) et l'échec (E).

Exemple :

$-\$ lancée d'une pièce de monnaie (Pile et Face)

$-\$ naissance d'un enfant (garçon ou fille)

$-\$ lancée de dé ; obtenir

$6$ ou ne pas obtenir

$6$

$-\$ tirage d'une boule ; obtenir une couleur donnée, ne pas obtenir cette couleur.

Considérons un nombre réel

$p\in[0\;,\ 1]$ et soit

$p(S)=p.$

On a

$p(S)+p(E)=1\ \Rightarrow\ p(E)=1-p(S).$ soit

$q$ cette probabilité.

Exemple :

Une expérience consiste à lancer un dé.

Soit les événements

$S=$ "obtenir la face

$6\$ " et

$\ \overline{S}$ = "ne pas obtenir la face

$6$ "

On a

$p(S)=\dfrac{1}{6}\;,\quad p(\overline{S})=\dfrac{5}{6}$

IV.2 Schéma de Bernoulli

Un schéma de Bernoulli est une répétition de

$n$ épreuves de Bernoulli identiques dans les mêmes conditions.

Exemple :

On lance

$6$ fois de suite un dé parfait numéroté de

$1$ à

$6.$

Quelle est la probabilité d'obtenir

$1(6)\;,\ 2(6)\;,\ 3(6)\ ?$

Résolution :

Soient les événements

$S=$ succès="obtenir le numéro

$6$ " et

$E=$ échec="ne pas obtenir le numéro

$6$ "

$-$ obtenir

$1(6)$ signifie avoir réalisé

$SEEEEE.$

Soit

$X$ le nombre de succès obtenus.

On a

$p(X=1)=\dfrac{1}{6}\times\left(\dfrac{5}{6}\right)^{5}\times C_{6}^{1}=0.40$

$-$ obtenir

$2$ fois le numéro

$6$ revient à observer

$SSEEEE.$

Donc

$p(X=2)=\left(\dfrac{1}{6}\right)^{2}\times\left(\dfrac{5}{6}\right)^{4}\times C_{6}^{2}=0.20$

$-$ obtenir

$3$ fois le numéro

$6$ équivaut à réaliser

$SSSEEE.$

Ainsi,

$p(X=3)=\left(\dfrac{1}{6}\right)^{3}\times\left(\dfrac{5}{6}\right)^{3}\times C_{6}^{3}=0.05$

Dans le cas général, la probabilité pour obtenir

$k$ succès sur les

$n$ épreuves est

$p(X=k)=C_{n}^{k}.(p(S))^{k}.(p(E))^{n-k}$

Or,

$p(E)=1-p(S)$

Donc,

$\boxed{p(X=k)=C_{n}^{k}.(p(S))^{k}.(1-p(S))^{n-k}}$

Exercice d'application

Une personne répond au hasard à

$20$ questions. Pour chaque question, on a une réponse juste et deux fausses.

Quelle est la probabilité pour qu'elle trouve

$2$ questions ?

$6$ questions ?

c) au moins

$2$ questions ?

Résolution :

Soient les événements

$S=$ succès="trouver la réponse" et

$E=$ échec="ne pas trouver la réponse".

Alors,

$p(S)=\dfrac{1}{3}$

On est en présence d'un schéma de Bernoulli.

Donc si

$X$ est le nombre de questions trouvées, alors

$p(X=2)=C_{20}^{2}\times\left(\dfrac{1}{3}\right)^{2}\times\left(\dfrac{2}{3}\right)^{18}=0.014$

$p(X=6)=C_{20}^{6}\times\left(\dfrac{1}{3}\right)^{6}\times\left(\dfrac{2}{3}\right)^{14}=0.18$

$\begin{array}{rcl} p(X\geq 2) &=& 1-p(X\leq 1) \\ \\ &=& 1-(p(X=0)+p(X=1)) \\ \\ &=& 1-C_{20}^{0}\times\left(\dfrac{1}{3}\right)^{0}\times\left(\dfrac{2}{3}\right)^{20}-C_{20}^{1}\times\left(\dfrac{1}{3}\right)^{1}\times\left(\dfrac{2}{3}\right)^{19} \\ \\ &=& 0.55 \end{array}$

V Variable aléatoire

V.1 Définition

Un variable aléatoire est une application

$\begin{eqnarray} X\ :\ \mathcal{P}(\Omega) & \longrightarrow & \mathbb{R} \nonumber \\ A &\longrightarrow & X(A) \nonumber \end{eqnarray}$

L'ensemble des valeurs prises par

$X$ est appelé univers image noté

$X(\Omega).$

Exemple :

Une urne contient

$6$ boules rouges,

$4$ boules noires et

$2$ boules vertes. On tire successivement

$3$ boules de l'urne en remettant la boule tirée dans l'urne après chaque tirage.

1) Soit

$X$ la variable aléatoire égale au nombre de boules noires tirées.

Déterminer

$X(\Omega)$

2) Si on tire

$3$ boules de même couleur , on perd

$200\;F$

Si on a

$2$ couleurs, on en gagne

$50\;F$

Si les

$3$ boules tirées sont de couleurs différentes, on gagne

$100\;F$

Soit

$Y$ , la valeur égale au gain du joueur.

Déterminer

$Y(\Omega)$

3) Pour chaque boule rouge tirée, le joueur gagne

$100\;F$ , chaque noire,

$50\;F$ et pour chaque boule verte il perd

$50\;F.$

Un joueur mise

$100\;F.$

Soit

$Z$ la valeur du gain.

Déterminer

$Z(\Omega)$

Solution :

$X(\Omega)=\{0\;,\ 1\;,\ 2\;,\ 3\}$

$Y(\Omega)=\{-200\;,\ 50\;,\ 100\}$

$Z(\Omega)=\{-250\;,\ -150\;,\ -100\;,\ -50\;,\ 0\;,\ 50\;,\ 100\;,\ 150\;,\ 200\}$

V.2 Loi de probabilité

Soit

$X$ une variable aléatoire d'univers image

$X(\Omega)=\{x_{1}\;,\ x_{2}\;,\ \ldots\;,\ x_{n}\}.$

La loi de probabilité est l'application qui associe à chaque

$x_{i}$ de

$X(\Omega)$ sa probabilité

$p(X=x_{i}).$

On le présente sous forme de tableau.

$\begin{array}{|c|c|c|c|c|c|c|} \hline x_{i} & x_{1} & x_{2} & x_{3} & \ldots & \ldots & x_{n} \\ \hline p(X=x_{i}) & & & & & & \\ \hline\end{array}$

Pour le 1) de notre exemple on a

$X(\Omega)=\{0\;,\ 1\;,\ 2\;,\ 3\}$

Ainsi,

$p(X=0)=\dfrac{8^{3}}{12^{3}}=\dfrac{8}{27}=0.29$

$p(X=1)=\dfrac{(4^{1}\times 8^{2})\times 3}{12^{3}}=\dfrac{4}{9}=0.44$

$p(X=2)=\dfrac{(4^{2}\times 8^{1})\times 3}{12^{3}}=\dfrac{2}{9}=0.22$

$p(X=3)=\dfrac{4^{3}}{12^{3}}=\dfrac{1}{27}=0.03$

$\begin{array}{|c|c|c|c|c|} \hline x_{i} & 0 & 1 & 2 & 3 \\ \hline p(X=x_{i}) & 8/27 & 4/9 & 2/9 & 1/27 \\ \hline\end{array}$

V.3 Espérance mathématique - Variance - Écart type

L'espérance mathématique d'une variable aléatoire

$X$ est le réel noté

$E(X)=\sum_{i=1}^{n}x_{i}.p(X=x_{i})=x_{1}.p(X=x_{1})+x_{2}.p(X=x_{2})+\ldots\ldots+x_{n}.p(X=x_{n})$

La variance d'une variable aléatoire

$X$ est le réel noté

$V(X)=E(X^{2})-(E(X))^{2}=\sum_{i=1}^{n}x_{i}^{2}.p(X=x_{i})-(E(X))^{2}$

et son écart type est noté

$\sigma(X)=\sqrt{V(X)}$

Remarque :

Une variable aléatoire

$X$ est dite centrée ou que le jeu est équitable si,

$E(X)=0$

$E(X)>0$ alors le jeu est favorable

$E(X)<0$ on dit que le jeu est défavorable

Exemple :

Considérons le 1) de l'exemple précédent alors, on a :

$\begin{array}{rcl} E(X) &=& \sum_{i=1}^{n}x_{i}.p(X=x_{i}) \\ \\ &=& 0\times\dfrac{8}{27}+1\times\dfrac{4}{9}+2\times\dfrac{2}{9}+3\times\dfrac{1}{27} \\ \\ &=& \dfrac{4}{9}+\dfrac{4}{9}+\dfrac{3}{27} \\ \\ &=& 1 \end{array}$

$\begin{array}{rcl} V(X) &=& E(X^{2})-(E(X))^{2} \\ \\ &=& \sum_{i=1}^{n}x_{i}^{2}.p(X=x_{i})-(E(X))^{2} \\ \\ &=& 0^{2}\times\dfrac{8}{27}+1^{2}\times\dfrac{4}{9}+2^{2}\times\dfrac{2}{9}+3^{2}\times\dfrac{1}{27}-1 \\ \\ &=& \dfrac{4}{9}+\dfrac{8}{9}+\dfrac{9}{27}-1=\dfrac{45}{27}-1 \\ \\ &=& \dfrac{2}{3} \end{array}$

$\sigma(X)=\sqrt{V(X)}=\sqrt{\dfrac{2}{3}}$

Remarque :

Pour un schéma de Bernoulli;

$p(S)=p\;,\ p(\overline{S})=1-p$

On a :

$p(X=k)=C_{n}^{k}.p^{k}.(1-p)^{n-k}$

Soit

$X$ la variable aléatoire égale au nombre de succès alors,

$X(\Omega)=\{0\;,\ 1\;,\ 2\;,\ \ldots\ldots\;,\ n\}$

Et on a :

$E(X)=\sum_{k=0}^{n}C_{n}^{k}.p^{k}.(1-p)^{n-k}=n.p$

$V(X)=np(1-p)$

V.4 Fonction de répartition

La fonction de répartition d'une variable aléatoire est la fonction définie sur

$\mathbb{R}$ par :

$p(X=x_{i})=p_{i}$

$F(x)=\left\lbrace\begin{array}{lcl} 0 &\text{si}& x<x_{1} \\ p_{1} &\text{si}& x_{1}\leq x<x_{2} \\ p_{1}+p_{2} &\text{si}& x_{2}\leq x<x_{3} \\ \vdots \\ p_{1}+p_{2}+p_{3}+\ldots+p_{k} &\text{si}& x_{k}\leq x<x_{k+1} \\ \vdots \\ p_{1}+p_{2}+p_{3}+\ldots+p_{n-1} &\text{si}& x_{n-1}\leq x<x_{n} \\ 1 &\text{si}& x\geq x_{n} \\ \end{array}\right.$

$F$ est une fonction en escalier.

Exemple :

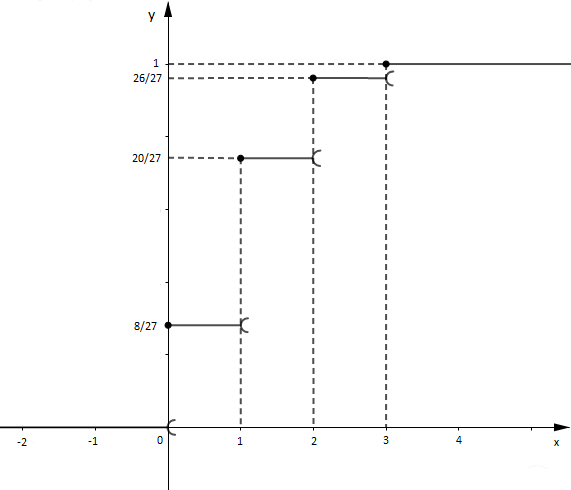
En considérant le 1) de l'exemple précédent on obtient

$\begin{array}{|c|c|c|c|c|} \hline x_{i} & 0 & 1 & 2 & 3 \\ \hline p(X=x_{i}) & 8/27 & 4/9 & 2/9 & 1/27 \\ \hline\end{array}$

Ce qui entraine

$F(x)=\left\lbrace\begin{array}{lcl} 0 &\text{si}& x<0 \\ \\ \dfrac{8}{27} &\text{si}& 0\leq x<1 \\ \\ \dfrac{20}{27} &\text{si}& 1\leq x<2 \\ \\ \dfrac{26}{27} &\text{si}& 2\leq x<3 \\ \\ 1 &\text{si}& x\geq 3 \\ \end{array}\right.$

Auteur:

Diny Faye & Seyni Ndiaye

Commentaires

Elève sérieux (non vérifié)

jeu, 03/27/2025 - 14:12

Permalien

besoin de ce support

bonjoir je vous remerci pour cet excellent résumé et vous sollicite pour m'envoyer le support du cours et vous en remercie d'avance

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Probabilités - T S

Formulaire de recherche

Exemple :

I Vocabulaire

I.1 Univers

I.2 Événement

Exemple :

Exemple :

Remarque :

Exemple :

Exemple :

Remarque :

II Définition et propriétés

II.1 Définition

II.2 Propriétés

II.3 Événements indépendants

Exercice d'application

Résolution

III Probabilités conditionnelles

Exemple :

Résolution :

III.1 Définition

III.2 Propriétés

IV Schéma de Bernoulli

IV.1 Épreuve de Bernoulli

Exemple :

Exemple :

IV.2 Schéma de Bernoulli

Exemple :

Résolution :

Exercice d'application

Résolution :

V Variable aléatoire

V.1 Définition

Exemple :

Solution :

V.2 Loi de probabilité

V.3 Espérance mathématique - Variance - Écart type

Remarque :

Exemple :

Remarque :

V.4 Fonction de répartition

Exemple :

Commentaires

besoin de ce support

Ajouter un commentaire

Plain text