Problèmes types du Bac

Dans la partie A de cet exercice, on étudie la fonction $f$ définie sur $]0;\ +\infty[$ par $f(x)=x+\dfrac{1}{x}+\dfrac{\ln x}{x^{2}}.$ Dans la partie B, on détermine la position de sa courbe représentative par rapport à son asymptote oblique.
 

Partie A

 

1) Soit $g$ la fonction définie sur $]0;\ +\infty[$ par $g(x)=x^{3}-x-2\ln x+1.$

 

a) Montrer que la fonction $g$ est dérivable sur sur $]0;\ +\infty[$ et que pour tout $x\in]0;\ +\infty[\;,$

$$g'(x)=\dfrac{(x-1)(3x^{2}+3x+2)}{x}$$

 

b) Étudier les variations de la fonction $g$ puis déterminer le signe de $g(x).$

 

2) a) Déterminer les limites de $f$ en 0 et en $+\infty$

 

b) Montrer que pour tout $x\in]0;\ +\infty[\;,$

$$f'(x)=\dfrac{g(x)}{x^{3}}$$ puis dresser le tableau de variation de la fonction $f.$

 

Partie B

 

$\mathcal{C}$ désigne la courbe représentative de $f$ dans un repère orthonormal $(O;\ \vec{i},\ \vec{j}).$

 

1) Soit $h$ la fonction définie sur pour tout $]0;\ +\infty[$ par $h(x)=x+\ln x.$

 

a) Étudier le sens de variation de $h$ puis montrer que l'équation $h(x)=0$ admet une solution unique $\alpha$ sur l'intervalle $[0.4;\ 0.7].$

 

b) Montrer que l'on a : $\mathrm{e}^{-\alpha}=\alpha.$

 

2) a) Vérifier que la droite $D$ d'équation $y=x$ est asymptote à la courbe $\mathcal{C}$ en $+\infty.$

 

b) Utiliser les résultats de la question 1)a) pour déterminer la position relative de $\mathcal{C}$ à $D.$

 

c) Construire $\mathcal{C}$ et $D$ dans le repère $(O;\ \vec{i},\ \vec{j}).$

$f$ est la fonction définie sur $\mathbb{R}_{+}^{*}$ par $f(x)=\dfrac{1}{2}\left(x+\dfrac{3}{x}\right).$

On note $\mathcal{C}$ la courbe représentative de $f$ dans un repère orthonormé direct $(O;\ \vec{i},\ \vec{j}).$

 

1) a) Établir le tableau de variation de $f$.

 

b) Vérifier que pour tout $x$ de l'intervalle  $[\sqrt{3},\ 2]\;,\ f(x)\in[\sqrt{3},\ 2].$

 

c) Vérifier que la droite $D$ d'équation $y=\dfrac{1}{2}x$ est asymptote à $\mathcal{C}.$

 

d) Soit $\Delta\ :\ y=x.$ Déterminer $\mathcal{C}\cap\Delta.$

 

e) Tracer $D\;,\ \Delta$ et $\mathcal{C}.$

 

2) Montrer que pour tout $x$ de $\mathbb{R}_{+}^{*}\;,\ f(x)-\sqrt{3}=\dfrac{(x-\sqrt{3})^{2}}{2x}.$

 

3) Soit $(x_{n})_{n\in\mathbb{N}}$ la suite définie par : $$\left\{\begin{array}{rcl} x_{0}&=& 2\\ \\ \forall\;n\in\mathbb{N}\;;\ x_{n+1} &=& \dfrac{1}{2}\left(x_{n}+\dfrac{3}{x_{n}}\right) \end{array}\right.$$

 

a) Représenter sur l'axe $(O;\ \vec{i})$ les premiers termes de la suite $(x_{n}).$

Faites une conjecture sur la suite $(x_{n}).$

 

b) Calculer les cinq premiers termes de la suite $(x_{n}).$

 

c) En se servant du 1)b), montrer à l'aide d'un raisonnement par récurrence que pour tout entier naturel $n\;,\ \sqrt{3}\leq x_{n}\leq 2.$

 

d) Déduire du 3)c), le sens de variation de la suite $(x_{n}).$

 

e) Démontrer que la suite $(x_{n})$ converge. Établir que sa limite est $\sqrt{3}.$

 

4) a) Montrer que pour tout entier naturel $n$,

$$|x_{n+1}-\sqrt{3}|\leq\dfrac{1}{2}(x_{n}-\sqrt{3})^{2}$$

 

b) En déduire que pour tout entier naturel non nul $n$,

$$|x_{n}-\sqrt{3}|\leq\left(\dfrac{1}{3}\right)^{2^{n}-1}$$

 

c) Retrouver à partir du 4)b) que $(x_{n})$ converge vers $\sqrt{3}.$

 

d) Déterminer un entier $k$ tel que pour tout entier naturel $n\;,\ n\geq k\;,\ $ $x_{n}$ est une valeur approchée de $\sqrt{3}$ à $10^{-11}$ près.

Le plan est rapporté au repère orthonormal $R=(O;\ \vec{i},\ \vec{j}).$

Soit $f$ la fonction définie sur $\mathbb{R}$ par : $$f(x)=\mathrm{e}^{x-1}-1$$

Le but du problème est de trouver une approximation de l'une des solutions de l'équation $f(x)=x.$

 

Partie A

 

On se propose d'étudier la fonction $f$ et les solutions de l'équation $f(x)=x.$

 

1) Établir le tableau de variation de $f$ et tracer sa courbe représentative $\mathcal{C}$ dans le repère $R.$

 

2) On pose $g(x)=f(x)-x.$

 

a) Déterminer la limite de $g$ lorsque $x$ tend vers $+\infty.$

 

b) Dresser le tableau de variation de $g$ et démontrer que l'équation $g(x)=0$ admet 2 solutions qu'on notera $a$ et $b\ (a<b).$

 

c) En déduire que l'équation $f(x)=x$ admet comme seules solutions $a$ et $b$ et établir que : $2<b<\dfrac{5}{2}.$

 

Partie B

 

On se propose d'étudier une méthode d'approximation du nombre $b.$

Pour ce faire on introduit les deux suites $(u_{n})_{n\geq 0}$ et $(v_{n})_{n\geq 0}$ définies comme suit : $u_{0}=2\;;\ v_{0}=\dfrac{5}{2}$ et pour tout entier $n\geq 1\;;$

$$\text{si }\ g\left(\dfrac{u_{n-1}+v_{n-1}}{2}\right)>0\ \text{ alors, }\ u_{n}=u_{n-1}\ \text{ et }\ v_{n}=\dfrac{u_{n-1}+v_{n-1}}{2}$$  

$$\text{si }\ g\left(\dfrac{u_{n-1}+v_{n-1}}{2}\right)\leq 0\ \text{ alors, }\ u_{n}=\dfrac{u_{n-1}+v_{n-1}}{2}\ \text{ et }\ v_{n}=v_{n-1}$$

 

1) Calculer $u_{1}\;,\ v_{1}\;,\ u_{2}\;,\ v_{2}.$

 

2) Soit $I=\left[2;\ \dfrac{5}{2}\right].$ Montrer en raisonnant par récurrence que pour tout entier naturel $n$, $u_{n}$ et $v_{n}$ sont éléments de $I.$

 

3) En utilisant le tableau de variations de la fonction $g$ sur l'intervalle $I$ et en raisonnant par récurrence, montrer que $(u_{n})$ est majorée par $b$ et que $(v_{n})$ est minorée par $b.$

 

4) Établir que la suite $(u_{n})$ est croissante et que la suite $(v_{n})$ est décroissante.

Que peut-on en conclure ? 

 

5) Démontrer par récurrence que : $$v_{n}-u_{n}=\left(\dfrac{1}{2}\right)^{n+1}$$

 

6) Montrer que les deux suites $(u_{n})_{n\geq 0}$ et $(v_{n})_{n\geq 0}$ convergent vers $b.$

 

7) Déterminer un entier positif $p$, tel que $v_{p}$ soit une valeur approchée à $10^{-1}$ près par excès de $b.$ Calculer $v_{p}.$

Partie A

 

$g$ est la fonction définie sur $]-1,\ +\infty[$ par $g(x)=\mathrm{e}^{x}-x-2.$

 

1) Étudier la fonction $g$.

 

2) Montrer que $g$ s'annule exactement une fois dans $]-1,\ +\infty[.$

On note $\alpha$ le réel de $]-1,\ +\infty[$ tel que $g(\alpha)=0.$

Donner un encadrement de $\alpha$ d'amplitude $10^{-3}.$

 

3) Déterminer le signe de $g(x)$ sur $]-1,\ +\infty[.$

 

Partie B

 

$g$ est la fonction définie sur $]-1,\ +\infty[$ par $f(x)=\dfrac{\mathrm{e}^{x}-x^{2}}{x+1}.$

 

1) Justifier que pour tout réel $x$ de $]-1,\ +\infty[\;,\ f'(x)=\dfrac{xg(x)}{(x+1)^{2}}.$

 

2) Établir le tableau de variation de la fonction $f.$

 

3) Montrer que $f(\alpha)=2-\alpha$ et en déduire un encadrement de $f(\alpha).$

 

4) Montrer que $$\lim_{x\rightarrow +\infty}\dfrac{f(x)}{x}=+\infty$$

 

5) Construire la courbe représentative $\Gamma$ de la fonction $f$ dans un repère orthogonal $(O;\ \vec{i},\ \vec{j}).$

la fonction $f$ définie sur $[0;\ +\infty[$ par $f(x)=\dfrac{x^{2}+x+1}{x^{2}}\mathrm{e}^{-\frac{1}{x}}$ pour $x>0$ et $f(0)=0.$

On note $\mathcal{C}$ la courbe représentative de $f$ dans un repère orthonormal $(O;\ \vec{i},\ \vec{j}).$

 

Partie A

 

1) Démontrer que la droite $(\Delta)$ d'équation $y=1$ est asymptote à $\mathcal{c}.$

 

2) Pour $x>0$, calculer $\dfrac{f(x)-f(0)}{x}$. Étudier la limite de cette expression quand $x$ tend vers 0.

Que peut-on déduire pour la fonction $f$ ?

Que peut-on en déduire pour la courbe $\mathcal{C}$ ?

 

3) Démontrer que pour tout $x$ de $]0;\ +\infty$ on a $f'(x)=\dfrac{1-x}{x^{4}}\mathrm{e}^{-\frac{1}{x}}.$

 

4) Étudier les variations de la fonction $f$ et dresser le tableau de variation de $f.$

 

Partie B

 

On note $g$ la fonction définie sur $]0;\ +\infty[$ par $g(x)=f(x)-xf'(x).$

 

1) Montrer que dans $]0;\ +\infty[$, les équations $g(x)=0$ et $x^{3}+x^{2}+2x-1=0$ sont équivalentes.

 

2) Démontrer que l'équation $x^{3}+x^{2}+2x-1=0$ admet une seule racine réelle $\alpha$ dont on justifiera un encadrement à $10^{-2}$ près.

 

3) On pose $A=\dfrac{f(\alpha)}{\alpha}$. Encadre $A$ à $2\times 10^{-1}$ près et montrer que $A=f'(\alpha).$

 

4) Pour tout $a>0$, on note $T_{a}$ la tangente à $\mathcal{C}$ au point d'abscisse $a.$

Montrer que $T_{\alpha}$ a pour équation $y=Ax$. Tracer $T_{\alpha}$ puis la courbe $\mathcal{C}.$

 

5) Déduire des équations précédentes que de toutes les tangentes $T_{a}$ à $\mathcal{C}$ (en des points d'abscisses non nulles), seule $T_{\alpha}$ passe par l'origine $O.$

 

6) On admettra que $T_{\alpha}$ est au-dessus de $\mathcal{C}$ sur $]0;\ +\infty[.$

 

a) Par lecture graphique (et sans justification), donner le nombre de solutions de l'équation $f(x)=m$, suivant le réel $m$ donné.

 

b) Par lecture graphique (et sans justification), donner le nombre de solutions de l'équation $f(x)=mx$, selon le réel $m$ donné. 

Préambule 

 

Soit $t$ un entier positif.

A l'instant $t$, une bactérie vit dans un milieu de culture.

A l'instant $t+1$, cette bactérie peut :

mourir avec une probabilité $\dfrac{1}{4}$, continuer à vivre avec une probabilité $\dfrac{1}{4}$, se diviser en deux bactéries identiques avec une probabilité $\dfrac{1}{2}.$

 

Partie A

 

On suppose dans cette partie, qu'à l'instant $t$, il y a deux bactéries $b_{1}$ et $b_{2}$, dans le milieu de culture, chacune se comportant de la même façon, décrite dans le préambule, et indépendamment l'une de l'autre.

On appelle $X$ le nombre total de bactéries à l'instant suivant $t+1.$

 

1) Quelles sont les valeurs possibles prises par $X$ ?

 

2) a) Décrire, à l'aide d'une phrase, l'événement $\{X=2\}.$

 

b) Justifier que la probabilité de l'événement $\{X=2\}$ est égale à $p(\{X=2\})=\dfrac{5}{16}.$

 

Partie B

 

On suppose dans cette partie, qu'à l'instant 0, il y a une seule bactérie dans le milieu de culture, qui se comporte comme décrit dans le préambule.

Ensuite, si à l'instant 1, il y a des bactéries, elles se comportent, à l'instant suivant comme la bactérie initiale et ceci, indépendamment les unes des autres.

Si à un instant, il n'y a plus de bactéries, le processus d'évolution s'arrête.

On se propose d'étudier le nombre de bactéries à l'instant 2.

 

1) On désigne par $A_{n}$ l'événement "à l'instant 1, il y a $n$ bactéries" et par  $B_{n}$ l'événement "à l'instant 2, il y a $n$  bactéries".

 

a) Donner la probabilité $p_{A_{1}}(B_{2})$ qu'il y ait deux bactéries à l'instant 2, sachant qu'il y avait une bactérie à l'instant 1.

 

b) Calculer la probabilité $p(A_{1}\cap B_{2})$ qu'il y ait une bactérie à l'instant 1 et deux bactéries à l'instant 2.

 

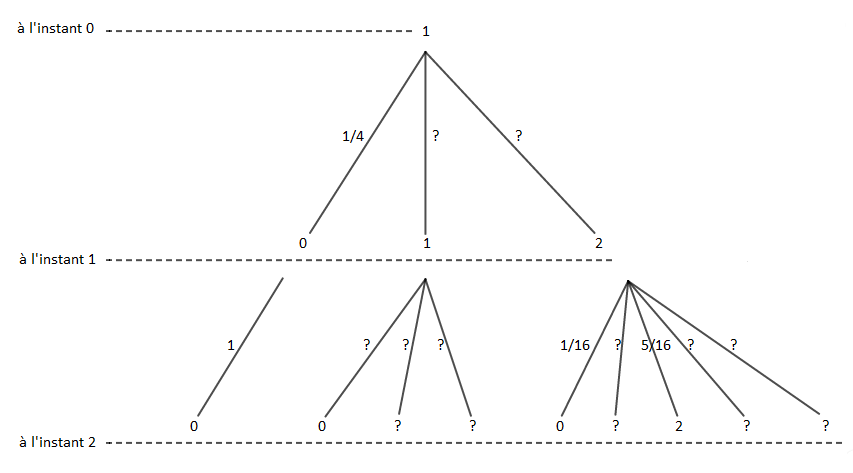
c) Compléter l'arbre donné en annexe en donnant toutes les possibilités pour le nombre de bactéries aux instants 1 et 2 et en inscrivant sur chaque branche de l'arbre, la probabilité correspondante.

 

2) On désigne par $A_{2}$ l'événement "à l'instant 1, il y a 2 bactéries".

 

a)  Donner la probabilité $p_{A_{2}}(B_{2})$ qu'il y ait deux bactéries à l'instant 2, sachant qu'il y avait deux bactéries à l'instant 1.

 

b) Calculer la probabilité $p(A_{2}\cap B_{2})$ qu'il y ait deux bactéries à l'instant 1 et deux bactéries à l'instant 2.

 

3) Soit $Y$ la variable aléatoire représentant le nombre de bactéries à l'instant 2.

 

a) Quelles sont les valeurs que peut prendre $Y$ ?

 

b) Calculer la probabilité de l'événement $\{Y=2\}.$

 

c) Calculer la probabilité de l'événement $\{Y=0\}.$

 

d) Faire un tableau donnant la loi de probabilité de $Y$.

 

e) Calculer l'espérance $E(Y)$ de $Y$.

 

Nombre de bactéries