Série d'exercices : Calcul vectoriel - 2nd
Classe:
Seconde
Exercice 1
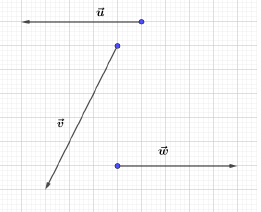
Dans chacun des cas suivants, reproduire le quadrillage, puis construire le vecteur $\vec{w}$ tel que $\vec{w}=\vec{u}+\vec{v}.$
a)

b)
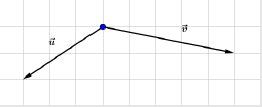
c)
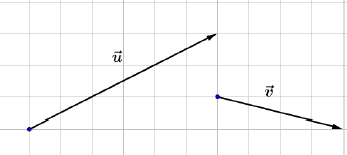
d)
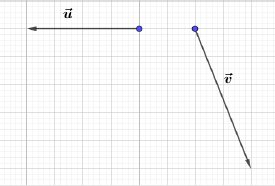
e)
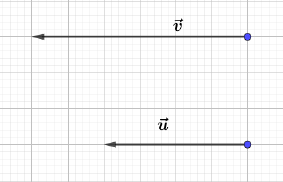
f)
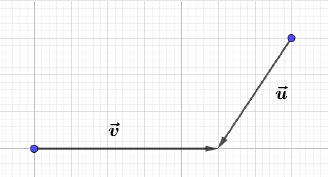
g)
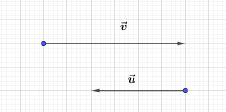
h)

Exercice 2
On considère la figure ci-dessous :
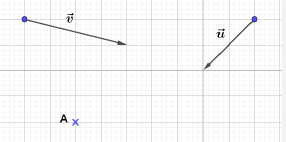
Construire les points $B\ $ et $\ C$ tels que : $\overrightarrow{AB}=\vec{u}+\vec{v}\ $ et $\ \overrightarrow{AC}=\vec{u}-\vec{v}$
Représenter les vecteurs $\vec{u}+\vec{v}\ $ et $\ \vec{u}-\vec{v}$
Exercice 3
Dans chacun des cas suivants, reproduire le quadrillage, puis construire le vecteur $\vec{u}+\vec{v}+\vec{w}$
a)
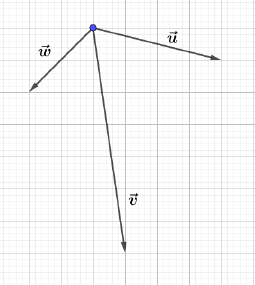
b)
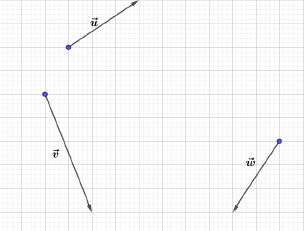
c)
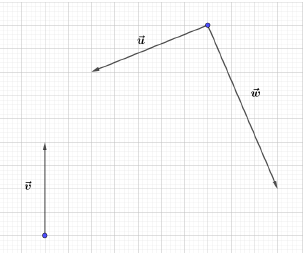
d)
Exercice 4
Soit $ABC$ un triangle. Construire les points $E\ $ et $\ F$ tels que : $\overrightarrow{AE}=\dfrac{4}{3}\overrightarrow{AB}\ $ et $\ \overrightarrow{BF}=-\dfrac{1}{2}\overrightarrow{AC}$
Exercice 5
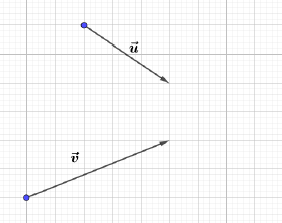
Sur une feuille à carreaux, reproduis la figure ci-dessous, puis construis des points $A\;,\ B\;,\ C\;,\ D$ tels que $\overrightarrow{AB}=5\vec{u}-\dfrac{7}{2}\vec{v}\ $ et $\ \overrightarrow{CD}=-3\vec{u}+2\vec{v}$
Exercice 6
On considère un triangle $ABC$ et on pose $\vec{u}=\overrightarrow{AB}\ $ et $\ \vec{v}=\overrightarrow{AC}.$
Construire les vecteurs $2\vec{u}-3\vec{v}\;,\ -\dfrac{3}{2}\vec{u}+2\vec{v}\;,\ -3\vec{u}-\dfrac{5}{2}\vec{v}.$
Exercice 7
Construire les points $E\ $ et $\ F$ tels que $\overrightarrow{DE}=\vec{w}-3\vec{u}\ $ et $\ \overrightarrow{DF}=-\dfrac{1}{2}\vec{w}+\vec{u}.$
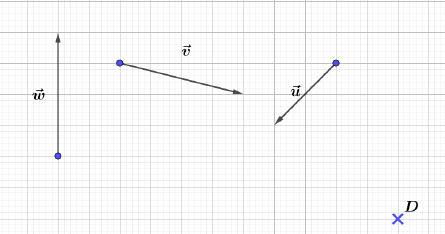
Exercice 8
Compéter à l'aide de la relation de Chasles :
a) $\overrightarrow{IL}=\overrightarrow{IK}+\overrightarrow{K\ldots}$
b) $\overrightarrow{CD}=\overrightarrow{CE}+\overrightarrow{\ldots D}$
c) $\overrightarrow{CD}=\overrightarrow{\ldots J}+\overrightarrow{\ldots}$
d) $\overrightarrow{...D}=\overrightarrow{C\ldots}+\overrightarrow{H\ldots}$
e) $\overrightarrow{CD}=\overrightarrow{\ldots A}+\overrightarrow{A\ldots}$
f) $\overrightarrow{H\ldots}=\overrightarrow{\ldots}+\overrightarrow{BD}$
g) $\overrightarrow{PQ}=\overrightarrow{P\ldots}+\overrightarrow{\ldots Q}$
h) $\overrightarrow{\ldots}=\overrightarrow{AB}+\overrightarrow{\ldots Q}$
i) $\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DJ}+\overrightarrow{JH}=\overrightarrow{\ldots}$
j) $\overrightarrow{AB}=\overrightarrow{\ldots K}+\overrightarrow{\ldots P}+\overrightarrow{\ldots}$
k) $\overrightarrow{\ldots A}=\overrightarrow{BD}+\overrightarrow{\ldots}+\overrightarrow{C\ldots}$
Exercice 9
On considère la figure ci-dessous constituée de triangles équilatéraux. Les points $A\;,\ B\;,...\;,\ L$ sont les sommets des précédents triangles.
Compléter
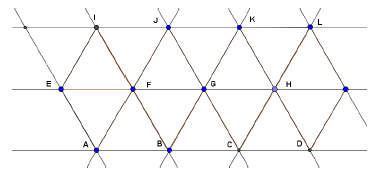
1) $\overrightarrow{AE}+\overrightarrow{AF}=\overrightarrow{A...}$
$\quad$
2) $\overrightarrow{AE}+\overrightarrow{EK}=\overrightarrow{A...}$
$\quad$
2) $\overrightarrow{AE}+\overrightarrow{EK}=\overrightarrow{A...}$
3) $\overrightarrow{EG}+\overrightarrow{GE}=\overrightarrow{\ldots}$
$\quad$
4) $\overrightarrow{EG}+\overrightarrow{AF}=\overrightarrow{E...}$
$\quad$
4) $\overrightarrow{EG}+\overrightarrow{AF}=\overrightarrow{E...}$
Exercice 10
$[AB]$ est un segment de longueur $8\;,cm.$ On se propose de construire un point $M$ tel que : $$\overrightarrow{MA}+3\overrightarrow{MB}=\vec{0}$$
a) Démontrer en utilisant la relation de Chasles que la relation ci-dessus s'écrit aussi : $$4\overrightarrow{MA}+3\overrightarrow{AB}=\vec{0}$$
b) En déduire l'expression de $\overrightarrow{AM}$ en fonction de $\overrightarrow{AB}$ et construire le point $M.$
Exercice 11
En utilisant la relation de Chasles, compléter les égalités suivantes :
a) $\overrightarrow{IJ}=\overrightarrow{IB}+\overrightarrow{B...}$
$\quad$
b) $\overrightarrow{CD}=\overrightarrow{...A}+\overrightarrow{A...}$
$\quad$
b) $\overrightarrow{CD}=\overrightarrow{...A}+\overrightarrow{A...}$
c) $\overrightarrow{MN}=\overrightarrow{...P}+\overrightarrow{\ldots}$
$\quad$
d) $\overrightarrow{...E}=\overrightarrow{F...}+\overrightarrow{P...}+\overrightarrow{G...}$
$\quad$
d) $\overrightarrow{...E}=\overrightarrow{F...}+\overrightarrow{P...}+\overrightarrow{G...}$
e) $\overrightarrow{H...}=\overrightarrow{\cdots}+\overrightarrow{IJ}$
$\quad$
f) $\overrightarrow{\ldots}=\overrightarrow{JK}+\overrightarrow{...M}$
$\quad$
f) $\overrightarrow{\ldots}=\overrightarrow{JK}+\overrightarrow{...M}$
g) $\overrightarrow{AB}+\overrightarrow{CD}+\overrightarrow{BC}=\overrightarrow{\ldots}$
$\quad$
h) $\overrightarrow{AB}=\overrightarrow{...C}+\overrightarrow{...D}+\overrightarrow{\ldots}$
$\quad$
h) $\overrightarrow{AB}=\overrightarrow{...C}+\overrightarrow{...D}+\overrightarrow{\ldots}$
Exercice 12
On donne un triangle $ABC$.
1) Démontrer que, lorsque $M$ varie dans le plan $\mathcal{P}$, le vecteur $\vec{v}_{_{M}}=2\overrightarrow{MA}-5\overrightarrow{MB}+3\overrightarrow{MC}$ reste constant. (Écrire $\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{AB}$ et $\overrightarrow{MC}=\overrightarrow{MA}+\overrightarrow{AC}$)
2) Même question pour le vecteur $-3\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}$
Exercice 13
On donne un triangle $ABC$. On considère les points $A'\;,\ B'\ $ et $\ C'$ tels que : $$\overrightarrow{AA}'=\dfrac{1}{3}\overrightarrow{BC}\;,\quad \overrightarrow{BB}'=\dfrac{1}{3}\overrightarrow{CA}\;,\quad \overrightarrow{CC}'=\dfrac{1}{3}\overrightarrow{AB}$$
Démontrer que : $\overrightarrow{AA}'+\overrightarrow{BB}'+\overrightarrow{CC}'=\vec{0}$
Exercice 14
$ABC$ est un triangle. $J$ est le point tel que $\overrightarrow{BJ}=\dfrac{2}{3}\overrightarrow{BC}.$
1) Exprimer $\overrightarrow{AJ}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}.$
2) Soit $I$ le point tel que $\overrightarrow{AI}=3\overrightarrow{AB}+2\overrightarrow{BC}.$
Montrer que les points $A\;,\ I\ $ et $\ J$ sont alignés.
Exercice 15
$IJK$ est un triangle. Les points $E\ $ et $\ F$ sont tels que :
$$\overrightarrow{IE}=\dfrac{2}{3}\overrightarrow{IJ}\ \text{ et }\ \overrightarrow{IF}=\dfrac{1}{3}\overrightarrow{IK}$$
$M$ est le milieu du segment $[IK].$
1) Exprimer $\overrightarrow{EF}\ $ et $\ \overrightarrow{JM}$ en fonction de $\overrightarrow{IJ}\ $ et $\ \overrightarrow{IK}$
2) Montrer que les droites $(EF)\ $ et $\ (JM)$ sont parallèles.
Exercice 16
$ABCD$ est un parallélogramme de centre $I.$ Les points $E\ $ et $\ F$ sont tels que $\overrightarrow{IE}=\dfrac{2}{3}\overrightarrow{DC}\ $ et $\ \overrightarrow{BF}=\dfrac{3}{2}\overrightarrow{BC}$
Exprimer $\overrightarrow{AE}\ $ et $\ \overrightarrow{AF}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}$
Exercice 17
$ABC$ est un triangle,$\alpha$ un nombre réel. On considère les points $P\;,\ Q\ $ et $\ R$ définis par : $$\overrightarrow{AP}=\alpha\overrightarrow{AB}\;,\quad \overrightarrow{CQ}=\alpha\overrightarrow{CA}\;,\quad \overrightarrow{CR}=\alpha\overrightarrow{BC}$$
1) Exprimer $\overrightarrow{PQ}\ $ et $\ \overrightarrow{PR}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$
2) Existe-t-il des valeurs de $\alpha$ pour que les points $P\;,\ Q\ $ et $\ R$ soient alignés ?
Exercice 18
$A\;,\ B\ $ et $\ C$ sont trois points non alignés. Les points $D\;,\ E\ $ et $\ F$ sont définis par les égalités de vecteurs suivants :
$$\overrightarrow{AD}=3\overrightarrow{AB}\;,\ \overrightarrow{AE}=\dfrac{3}{2}\overrightarrow{AC}\;,\ \overrightarrow{BF}=2\overrightarrow{BC}$$
1) Exprimer $\overrightarrow{DE}\ $ et $\ \overrightarrow{DF}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$
$$\overrightarrow{AD}=3\overrightarrow{AB}\;,\ \overrightarrow{AE}=\dfrac{3}{2}\overrightarrow{AC}\;,\ \overrightarrow{BF}=2\overrightarrow{BC}$$
1) Exprimer $\overrightarrow{DE}\ $ et $\ \overrightarrow{DF}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AC}$
2) Montrer que les points $D\;,\ E\ $ et $\ F$ sont alignés.
Exercice 19
Le segment $[AB]$ est divisé en 6 parties de même longueur. Compléter les relations suivantes par la lettre ou le nombre qui convient.

1) $EC=...EF\quad$ 2) $C...=...G$
$\quad$
3) $AB= A...\quad$ 4) $CE=...AB$
$\quad$
5) $AD=...BF\quad$ 6) $DE=...BF$
$\quad$
3) $AB= A...\quad$ 4) $CE=...AB$
$\quad$
5) $AD=...BF\quad$ 6) $DE=...BF$
Exercice 20
$ABCD$ est un parallélogramme. Les points $E\ $ et $\ F$ sont tels que :
$$\overrightarrow{DE}=\dfrac{2}{3}\overrightarrow{DC}\ \text{ et }\ \overrightarrow{BF}=\dfrac{3}{2}\overrightarrow{BC}$$
1) Exprimer $\overrightarrow{AE}\ $ et $\ \overrightarrow{AF}$ en fonction de $\overrightarrow{AB}\ $ et $\ \overrightarrow{AD}$
2) Montrer que les points $A\;,\ E\ $ et $\ F$ sont alignés.
Exercice 21
Soit $ABC$ un triangle quelconque.
1) Construire les points $D$ et $E$ tels que $\overrightarrow{AD}=\overrightarrow{BC}\;,\quad\overrightarrow{CE}=2\overrightarrow{BA}$
2) Démontrer que $D$ est le milieu de $[CE]$
Exercice 22
Soit $ABC$ un triangle. Construire les points $M$ et $N$ tels que : $$\left\lbrace\begin{array}{rcl}\overrightarrow{AN}+\overrightarrow{AM}&=&\overrightarrow{AB} \\ \overrightarrow{AN}-\overrightarrow{AM}&=&\overrightarrow{AC}\end{array}\right.$$
Exercice 23
Construire trois vecteurs $\vec{u}\;,\ \vec{v}$ et $\vec{w}$ tels que $$\left\lbrace\begin{array}{rcl}\vec{u}+\vec{v}-2\vec{w}&=&\vec{0} \\ \vec{u}-\vec{v}+\vec{w}&=&\vec{0}\end{array}\right.$$
Démontrer que $\vec{u}$ et $\vec{v}$ sont colinéaires au vecteur $\vec{w}$
Exercice 24
Soit $A$ et $B$ deux points distincts du plan, $I$ milieu de $[AB]$
1) Démontrer que pour tout point $M$ du plan $$\overrightarrow{AM}+\overrightarrow{BM}=2\overrightarrow{IM}$$
2) Déterminer et construire l'ensemble $\mathcal{C}$ des points $M$ du plan tels que $$||\overrightarrow{AM}+\overrightarrow{BM}||=2AB$$
Exercice 25
Soit un triangle $DIM$ et soit $A$ le milieu de $[DM]$
a) Construire les points $T$ et $H$ tels que $\overrightarrow{DT}=4\overrightarrow{DI}$ et $\overrightarrow{IH}=3\overrightarrow{IM}$
b) Démontrer que $(TH)//(IA)$
Exercice 26
Soit $ABC$ un triangle quelconque.
1) a) Montrer que l'égalité $\overrightarrow{DA}-3\overrightarrow{DB}+\overrightarrow{DC}=\vec{0}$ équivaut à l'égalité $\overrightarrow{AD}=3\overrightarrow{AB}-\overrightarrow{AC}.$ Construire le point $D.$
b) Montrer que $\overrightarrow{MA}-3\overrightarrow{MB}+\overrightarrow{MC}=-\overrightarrow{MD}$ quelque soit le point $M$
c) Montrer que $\overrightarrow{BA}+\overrightarrow{BC}=-\overrightarrow{BD}$
2) Soit $M$ un point quelconque, on pose $\vec{V}=\overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC}$
Montrer que $\vec{V}=\overrightarrow{BA}+\overrightarrow{BC}$ et placer le point $E$ défini par $\vec{V}=\overrightarrow{AE}$
3) Montrer que les droites $(BD)$ et $(AE)$ sont parallèles
Exercice 27
Soit $ABC$ un triangle
1) Construire les points $M$ et $N$ tels que $\overrightarrow{AM}=-\dfrac{2}{3}\overrightarrow{AB}$ et $\overrightarrow{AN}=-\dfrac{2}{3}\overrightarrow{AC}$
2) Démontrer que $(MN)//(BC)$
3) Soient $S$ et $T$ les milieux respectifs de $[BC]$ et $[MN].$ Démontrer que les points $A\;,\ S$ et $T$ sont alignés.
Exercice 28
Soit $ABC$ un triangle de centre de gravité $G$ et $I$ milieu de $[BC]$
1) Démontrer que pour tout point $M$ du plan $$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}\ ;$$ $$2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}=2\overrightarrow{IA}$$
2) Quel est l'ensemble des points $M$ tels que les vecteurs $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$ et $2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}$ soient colinéaires.
3) Quel est l'ensemble des points $M$ tels que $$||\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}||=||2\overrightarrow{MA}-\overrightarrow{MB}-\overrightarrow{MC}||$$
Exercice 29
$ABCD$ est un parallélogramme, $I$ milieu de $[AB]$ et $J$ celui de $[CD]$
1) Démontrer que les droites $(ID)$ et $(JB)$ sont parallèles.
2) a) Construire les points $M$ et $N$ tels que $\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AC}$ et $\overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AC}$
b) Démontrer que les points $M$ et $N$ appartiennent respectivement aux droites $(ID)$ et $(JB)$
3) Démontrer que $MINJ$ est un parallélogramme
4) Soit $\{E\}=(ID)\cap(BC)$, montrer que $B$ est milieu de $[CE]$
Exercice 30
$ABCD$ est un parallélogramme, $E$ et $F$ deux points définis par $\overrightarrow{AE}=-\dfrac{1}{2}\overrightarrow{AD}$ et $\overrightarrow{EF}=\dfrac{1}{2}\overrightarrow{BA}$
1) Exprimer $\overrightarrow{AC}$ et $\overrightarrow{AF}$ en fonction de $\overrightarrow{AB}$ et $\overrightarrow{AD}$
2) Démontrer que les points $A\;,\ F$ et $C$ sont alignés
3) Exprimer les coordonnées de $A\;,\ F$ et $C$ dans le repère $(A\;;\ \overrightarrow{AB}\;,\ \overrightarrow{AD})$ puis calculer les coordonnées de $\overrightarrow{AF}$ et $\overrightarrow{AC}$
Exercice 31
Soit $ABCD$ un parallélogramme. On considère $E$ défini par $\overrightarrow{CE}=\overrightarrow{DA}-\dfrac{1}{2}\overrightarrow{AB}$ et le point $F$ symétrique de $D$ par rapport à $E$
1) Démontrer que $E$ est le milieu de $[AB]$ et $B$ le milieu de $[CF]$
2) Démontrer que $ADBF$ est un parallélogramme
Exercice 32
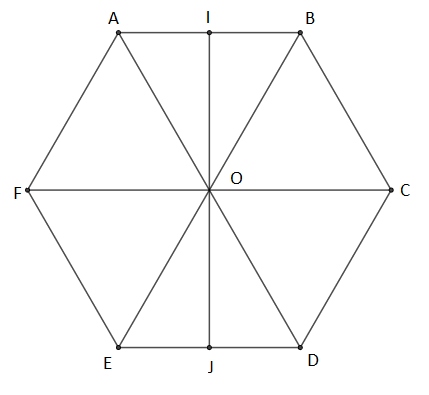
On considère l'hexagone régulier $ABCDEF$ de centre $O$ ci-dessus, et $I$ et $J$ les milieux respectifs des segments $[AB]$ et $[ED].$ En utilisant les lettres de la figure citer :
a) deux vecteurs égaux
b) deux vecteurs colinéaires de sens contraire et normes distinctes.
c) deux vecteurs colinéaires de même sens et de normes différentes.
d) deux vecteurs orthogonaux.
e) deux vecteurs non colinéaires et de même norme.
f) deux vecteurs opposés.
g) deux vecteurs non colinéaires et de norme distinctes.
Exercice 33
On considère la figure ci-dessous :
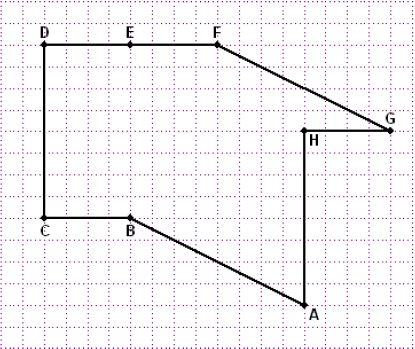
1) Citer tous les vecteurs égaux à $\overrightarrow{AB}.$
2) Citer tous les vecteurs égaux à $\overrightarrow{FE}.$
3) Déterminer un ou plusieurs vecteurs égaux à $\overrightarrow{AB}+\overrightarrow{FE}.$
4) Déterminer un vecteur égal aux vecteurs suivants :
a) $\overrightarrow{AB}+\overrightarrow{AH}\quad$ b) $\overrightarrow{BA}+\overrightarrow{BC}$
$\quad$
c) $\overrightarrow{BC}+\overrightarrow{DE}$
$\quad$
c) $\overrightarrow{BC}+\overrightarrow{DE}$
d) $\overrightarrow{BF}+\overrightarrow{GF}\quad$ e) $\overrightarrow{AE}+\overrightarrow{FB}$
N.B. Pour chacune des réponses, on utilisera uniquement les lettres de la figure.
Exercice 34
$A\;,\ B\;,\ C\;,\ D$ sont quatre points. Démontrer que :
1) $\overrightarrow{AB}-\overrightarrow{CD}-(\overrightarrow{AB}-\overrightarrow{CA})=\overrightarrow{DA}$
2) $\overrightarrow{AD}+\overrightarrow{BC}=(\overrightarrow{AC}+\overrightarrow{BD})$
Exercice 35
Écrire les vecteurs suivants en utilisant le moins de vecteurs possibles :
$\vec{u}=\overrightarrow{DE}+\overrightarrow{AB}-\overrightarrow{DB}$ (1 vecteur)
$\vec{v}=2(\overrightarrow{AB}+\overrightarrow{AC})+\overrightarrow{BC}$ (2 vecteurs)
$\vec{w}=\dfrac{1}{2}\overrightarrow{BA}-2\left(\overrightarrow{DB}-\dfrac{1}{4}\overrightarrow{AC}\right)$ (2 vecteurs)
Exercice 36
$O$ et $A$ sont deux points distincts :
1) Placer les points $M\;,\ N\;,\ P$ tels que :
a) $\overrightarrow{OM}=2\overrightarrow{OA}\quad$ b) $\overrightarrow{ON}=-3.5\overrightarrow{OA}\quad$ c) $\overrightarrow{OP}=-7\overrightarrow{OA}$
2) a) Exprimer le vecteur $\overrightarrow{OM}+\overrightarrow{ON}$ en fonction de $\overrightarrow{OA}.$
b) Exprimer le vecteur $\overrightarrow{OP}$ en fonction de $\overrightarrow{ON}.$
Exercice 37
$A\;,\ B\;,\ C$ et $D$ sont quatre points quelconques du plan.
1) Construire les points $R$ et $S$ tels que $\overrightarrow{AR}=\overrightarrow{AB}+\overrightarrow{CD}$ et $\overrightarrow{AS}=\overrightarrow{AD}+\overrightarrow{CB}.$
Quelle remarque peut-on faire ?
2) Démontrer que $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}.$
Exercice 38
$ABCD$ est un parallélogramme de centre $O.$
1) Calculer la somme vectorielle $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}.$
2) $M$ étant un point quelconque du plan, placer les points $E\;,\ F\;,\ G$ et $H$ tels que :
$\overrightarrow{ME}=\overrightarrow{AB}\;;\ \overrightarrow{MF}=\overrightarrow{BC}\;;\ \overrightarrow{MG}=\overrightarrow{CD}$ et $\overrightarrow{MH}=\overrightarrow{DA}$
Démontrer que le quadrilatère $EFGH$ est un parallélogramme.
Exercice 39
$OAB$ est un triangle, $D$ et $C$ les points tels que : $\overrightarrow{OD}=\overrightarrow{OA}+\overrightarrow{OB}$ et $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\vec{0}.$
1) Démontrer que $O$ est le milieu de $[CD].$
2) $E$ et $F$ sont les points tels que : $\overrightarrow{OE}=\overrightarrow{OA}+\overrightarrow{OC}$ et $\overrightarrow{OF}=\overrightarrow{OB}+\overrightarrow{OC}.$ Démonter que $ABFE$ est un parallélogramme.
Exercice 40
$A\;,\ B\;,\ C\;,\ D$ sont quatre points
1) Construire les points $E\;,\ F$ tels que
$\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{AC}-\overrightarrow{BC}$ et $\overrightarrow{AF}=\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{AD}.$
2) Montrer que $\overrightarrow{FE}=\overrightarrow{AC}+\overrightarrow{DB}$
Exercice 41
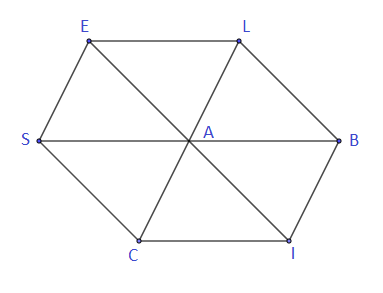
Sur la figure, les quadrilatères $SALE\;,\ SAIC\;,\ SCAE\;,\ BAEL\;,\ LAIB$ et $BACI$ sont des parallélogrammes.
En n'utilisant que les points de la figure, écrire chacune des sommes suivantes sous forme d'un seul vecteur.
$\overrightarrow{AB}+\overrightarrow{AL}\;,\quad \overrightarrow{AB}+\overrightarrow{BL}+\overrightarrow{LA}\;,\quad \overrightarrow{AB}-\overrightarrow{AL}$
$\overrightarrow{AB}+\overrightarrow{AL}+\overrightarrow{AE}\;,\quad \overrightarrow{AE}-(\overrightarrow{CA}+\overrightarrow{SC})\;,\quad \overrightarrow{SA}-\overrightarrow{LB}$
$\overrightarrow{SI}-\overrightarrow{EL}-\overrightarrow{SL}\;,\quad \overrightarrow{SI}-\overrightarrow{EL}+\overrightarrow{SL}$
Exercice 42
Simplifier au maximum l'écriture des vecteurs suivants en utilisant la relation de Chasles :
1) $\vec{u}=\overrightarrow{AB}-\overrightarrow{AC}-\overrightarrow{CB}\;;\quad\vec{v}=\overrightarrow{BC}-\overrightarrow{BA}-\overrightarrow{BD}-\overrightarrow{BC}$
$\vec{w}=\overrightarrow{AB}-\overrightarrow{AC}-\overrightarrow{CB}\;;\quad\vec{t}=\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{AB}$
2) $\vec{u}=\overrightarrow{DA}+\overrightarrow{BC}+\overrightarrow{CD}\;;\quad\vec{v}=\overrightarrow{AB}+\overrightarrow{BC}-\overrightarrow{CD}+\overrightarrow{AD}$
$\vec{w}=\overrightarrow{AC}+2\overrightarrow{CB}+\overrightarrow{BA}\;;\quad\vec{t}=2\overrightarrow{AB}-\overrightarrow{BC}-\overrightarrow{CA}$
3) en fonction de $\overrightarrow{AB}$ et $\overrightarrow{AC}$
$\vec{u}=2\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}+\overrightarrow{BC}\;;\quad\vec{v}=\overrightarrow{BA}+3\overrightarrow{CA}-2\overrightarrow{BC}$
$\vec{w}=\dfrac{2}{5}(\overrightarrow{AB}-5\overrightarrow{BC})+\overrightarrow{CA}\ ;$
$\quad$
$\vec{t}=2(\overrightarrow{MB}-\overrightarrow{AC})+\overrightarrow{MB}-3\overrightarrow{MC}$
$\quad$
$\vec{t}=2(\overrightarrow{MB}-\overrightarrow{AC})+\overrightarrow{MB}-3\overrightarrow{MC}$
Exercice 43
$ABC$ est un triangle. Exprimer le vecteur $\overrightarrow{AM}$ en fonction de $\overrightarrow{AB}$ et $\overrightarrow{AC}$ et construire le point $M$ dans
chacun des cas suivants :
a) $\overrightarrow{AM}+\overrightarrow{BC}=\overrightarrow{AB}\ ;$
$\quad$
b) $2\overrightarrow{MA}+\overrightarrow{AC}=\overrightarrow{AB}$
$\quad$
b) $2\overrightarrow{MA}+\overrightarrow{AC}=\overrightarrow{AB}$
c) $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{AC}\ ;$
$\quad$
d) $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}$
$\quad$
d) $\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\vec{0}$
Exercice 44
$ABCD$ est un parallélogramme, $I$ et $J$ les points tels que :
$\overrightarrow{AI}=\dfrac{1}{2}\overrightarrow{AB}\;;\ \overrightarrow{AJ}=\dfrac{1}{3}\overrightarrow{AD}.$
Soit $G$ le point tels que : $\overrightarrow{IG}=\dfrac{3}{5}\overrightarrow{IJ}.$
Construire la figure et monter que les points $A\;,\ C\;,\ G$ sont alignés.
Exercice 45
Dans un triangle $ABC$, on considère par $M$ le milieu de $[AB]$, par $I$ celui de $[MC]$ et $K$ le point tel que $\overrightarrow{CK}=\dfrac{1}{3}\overrightarrow{CB}$
1) Montrer que $\overrightarrow{AI}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}$ et $\overrightarrow{AK}=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}.$
2) En déduire que les points $A\;,\ I\;,\ K$ sont alignés.
Exercice 46
$ABC$ un triangle,$O$ un point quelconque, $G$ et $P$ les points tels que :
$\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AB}$ et $\overrightarrow{OP}=\overrightarrow{OA}+2\overrightarrow{OB}-3\overrightarrow{OC}$
1) Montrer que $3\overrightarrow{OG}=\overrightarrow{OA}+2\overrightarrow{OB}.$
2) Montrer que les droites $(OP)$ et $(CG)$ sont parallèles.
Exercice 47
Soit $ABCD$ un parallélogramme, $E$ le milieu de $[BC]$ et $F$ le milieu de $[DC].$
1) Démontrer que $\overrightarrow{AC}+\overrightarrow{BD}=2\overrightarrow{BC}$
2) Démontrer que $\overrightarrow{AE}+\overrightarrow{AF}=\dfrac{3}{2}\overrightarrow{AC}.$
Exercice 48 Caractérisation du milieu d'un segment
1) Soit $[AB]$ un segment et $I$ son milieu. Démontrer que :
si $M$ est un point quelconque du plan, alors : $2\overrightarrow{MI}=\overrightarrow{MA}+\overrightarrow{MB}$
2) Soit $[AB]$ un segment et $M$ un point quelconque du plan. Démontrer que, si le point $I$ est défini par la relation vectorielle : $$2\overrightarrow{MI}=\overrightarrow{MA}+\overrightarrow{MB}$$ alors $I$ est le milieu du segment $[AB].$
Exercice 49
1) Soit $ABC$ un triangle, $I$ le milieu de $[AB]$ et $J$ le milieu de $[AC].$
Montrer que $\overrightarrow{IJ}=\dfrac{1}{2}\overrightarrow{BC}.$
2) Soit $ABDC$ un quadrilatère quelconque, $I\;,\ J\;,\ K$ et $L$ les milieux respectifs de $[AB]$, de $[AC]$, de $[DB]$ et de $[DC].$
Démontrer que $IJKL$ est un parallélogramme (on pourra utiliser la question 1).
Quelle condition faut-il rajouter sur $ABDC$ pour que $IJKL$ soit un losange ? un rectangle ? un carré ?
Exercice 50
$ABCD$ un parallélogramme de centre $O\;,\ E$ est le milieu de $[AB]\;,\ F$ celui de $[CD].$ Les droites $(DE)$ et $(BF)$ coupent la droite $(AC)$ en $L$ et $M$ respectivement.
1) Montrer que $L$ est centre de gravité du triangle $ABD.$
En déduire que $\overrightarrow{OL}=\dfrac{1}{3}\overrightarrow{OA}.$
2)Prouver que $\overrightarrow{OM}=\dfrac{1}{3}\overrightarrow{OC}$ et que $O$ est le milieu de $[ML]$
Exercice 51 $\begin{array}{c}\blacktriangleright\,\boxed{\text{Corrigé}}\end{array}$
$ABCD$ est un trapèze tel $\overrightarrow{BC}=2\overrightarrow{AD}\;,\ k$ est un nombre réel et $M$ le point défini par $\overrightarrow{AM}=k\overrightarrow{AB}$ se projette en $K$ sur $(AC)$ parallèlement à $(BC)$ et en $N$ sur $(CD)$ parallèlement à $(BC).$
1) Montrer que $\overrightarrow{MK}=2k\overrightarrow{AD}$ et $\overrightarrow{NK}=(k-1)\overrightarrow{AD}.$
2) Déterminer le réel $k$ pour que $K$ soit le milieu de $[MN]$, puis pour que $\overrightarrow{MN}=\dfrac{3}{2}\overrightarrow{AD}$
Exercice 52
Soit $ABCD$ un carré. On construit sur $[DC]$ et à l'intérieur du carré le triangle équilatéral $DCE.$
On construit sur $[BC]$ et à l'extérieur du carré le triangle équilatéral $BCF.$
1) Exprimer les vecteurs $\overrightarrow{AE}$ et $\overrightarrow{AF}$ en fonction des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AD}.$
2)En déduire que les points $A\;,\ E\;,\ F$ sont alignés.
Exercice 53
Soit un triangle $ABC\;;\ D$ et $E$ les symétriques de $B$ par rapport à $A$ et $C\;;\ F$ et $G$ les milieux des
segments $[DC]$ et $[AE].$
On désigne par $M$ le point d'intersection de $(BF)$ et $(AC)\;,\ N$ celui de $(BG)$ et $(AC).$
Montrer que l'on a $\overrightarrow{AM}=\overrightarrow{MN}=\overrightarrow{NC}.$
On désigne par $I$ et $J$ les milieux de $[AD]$ et $[CE].$
Montrer que les points $I\;,\ F\;,\ G\;,\ J$ sont alignés et que :
$\overrightarrow{IF}=\overrightarrow{FG}=\overrightarrow{GJ}.$
On désigne par $K$ le milieu de $[BF].$ Montrer que les points $K\;,\ N$ et $J$ sont alignés.
On désigne par $P$ le point d'intersection de $(DC)$ et $(AE).$ Montrer que $(MN)$ est parallèle à $(BC).$
Déterminer le réel $\alpha$ tel que $\overrightarrow{BK}=\alpha\overrightarrow{BM}.$
Exercice 54
Soit $ABCD$ un parallélogramme et les points $I$ et $J$ milieux respectifs des segments $[AB]$ et $[CD].$
1) Démontrer que les droites $(ID)$ et $(JB)$ sont parallèles.
2) Construire les points $M$ et $N$ tels que :
$\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AC}$ et $\overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AC}.$
3) Exprimer $\overrightarrow{IM}$ et $\overrightarrow{ID}$ en fonction des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}.$
En déduire que $M$ appartient à la droite $(ID).$
4) Exprimer $\overrightarrow{BJ}$ et $\overrightarrow{BN}$ en fonction des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}.$
En déduire que $N$ appartient à la droite $(JB).$
5) Démontrer que $MINJ$ est un parallélogramme.
6) Soit $E$ le point d'intersection des droites $(ID)$ et $(BC).$
Démontrer que $B$ est le milieu du segment $[CE].$
Exercice 55
Soit $ABC$ un triangle non rectangle ; $O$ le centre et $r$ le rayon de son cercle circonscrit $\mathcal{C}.$
1) On considère le point $H$ défini par : $\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}.$
a) Montrer que : $\overrightarrow{AH}=2\overrightarrow{OA}'\;,\ \overrightarrow{BH}=2\overrightarrow{OB}'$ et $\overrightarrow{CH}=2\overrightarrow{OC}'$, avec $A'\;,\ B'\;,\ C'$ milieux respectifs de $[BC]\;,\ [CA]$ et $[AB].$
b) En déduire que : $(AH)\perp(BC)$ et $(BH)\perp(CA).$
Que représente alors le point $H\;$ ?
2) On désigne par $I\;,\ J\;,\ K$ les milieux de $[AH]\;,\ [BH]\;,\ [CH].$ Montrer que les segments $[OH]\;,\ [IA']\;,\ [JB']\;,\ [KC']$ ont le même milieu $\Omega.$
3) Montrer que : $\overrightarrow{\Omega I}=\dfrac{1}{2}\overrightarrow{OA}\;,\ \overrightarrow{\Omega J}=\dfrac{1}{2}\overrightarrow{OB}$ et $\overrightarrow{\Omega K}=\dfrac{1}{2}\overrightarrow{OC}.$
En déduire que les points $I\;,\ J\;,\ K$ appartiennent au cercle $\mathcal{C}'$ de centre $\Omega$ et de rayon $\dfrac{1}{2}r.$
4) Montrer que : $\overrightarrow{\Omega A}'=-\dfrac{1}{2}\overrightarrow{OA}\;,\ \overrightarrow{\Omega B}'=-\dfrac{1}{2}\overrightarrow{OB}$ et $\overrightarrow{\Omega C}'=-\dfrac{1}{2}\overrightarrow{OC}$
En déduire que les points $A'\;,\ B'\;,\ C'$ appartiennent au cercle $\mathcal{C}'.$
5) On désigne par $A_{1}\;,\ B_{1}\;,\ C_{1}$ les pieds sur $(BC)\;,\ (CA)\;,\ (AB)$ des hauteurs du triangle $ABC.$
Montrer que les points $A_{1}\;,\ B_{1}$ et $C_{1}$ sont éléments du cercle $\mathcal{C}'.$
6) Soit $G$ le centre de gravité du triangle $ABC.$ Montrer que les points $O\;,\ G$ et $H$ sont alignés.
7) Les résultats précédents sont-ils vérifiés lorsque le triangle $ABC$ est rectangle ? Faire par exemple une figure avec le triangle $ABC$ rectangle en $A.$
Que dire des points $O\;,\ G\;,\ H\;,\ \Omega$, lorsque le triangle $ABC$ est équilatéral ?
Notes :
$\centerdot\ \mathcal{C}'$ est appelé cercle d'Euler du triangle $ABC.$
$\centerdot\ $ Lorsque le triangle $ABC$ n'est pas équilatéral, la droite $(OH)$ est appelée droite d'Euler de $ABC.$

Commentaires
M Dramé (non vérifié)
dim, 12/22/2019 - 21:03
Permalien
Demande d'assistance sur lexo 58.
Anonyme (non vérifié)
sam, 01/04/2020 - 23:49
Permalien
J'adores bien
Adja (non vérifié)
mer, 12/16/2020 - 22:20
Permalien
Demande d aide
Anononyme23 (non vérifié)
mer, 12/16/2020 - 22:22
Permalien
Demande d aide
Omar Fall (non vérifié)
dim, 03/13/2022 - 23:08
Permalien
Demande d'aide
Mia Piar (non vérifié)
dim, 03/13/2022 - 23:10
Permalien
Demande d'aide
Anonyme (non vérifié)
ven, 12/06/2024 - 19:11
Permalien
excellent
Ajouter un commentaire