Série d'exercices : Fonction affine et droite du plan - 2nd L
Exercice 1
Représente graphiquement dans un repère orthonormé $\left(O\ ;\ \vec{I}\ ;\ \vec{J}\right)$ chacune des fonctions affines ou linéaires puis donne le le coefficient et la constante.
a. $f(x)=3x$
b. $(x)=2x+3$
c. $f(x)=-\dfrac{3}{2}x$
d. $f(x)=-\dfrac{1}{3}x+4$
Exercice 2:
Dites si les fonctions suivantes sont-elles des fonctions affines ou linéaires , et le cas échéant , précise $m$ et $P.$
a. $f(x)=x$
b. $f(x)=2+x$
c. $f(x)=-\dfrac{7x}{3}+4$
d. $f(x)=-4x^{3}+2$
a. $f(x)=3x+8$
b. $f(x)=x-1$
c. $f(x)=-\dfrac{7x}{3}$
d. $f(x)=-4x^{2}+2x+1$
2. Dites si les représentations graphiques sont-elles des fonctions affines ou linéaires.
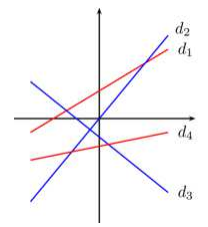
Exercice 3:
Soit $f$ la fonction affine définie par :
$f(x)=-\dfrac{3x}{2}-1$
Calculer les images des nombres :
$-3\ ;\ \dfrac{2}{3}$ et $2$ par $f$ et les antécédents des nombres :
$-2$ et $\dfrac{8}{7}$ par $f.$
Exercice 4:
Calcul du taux d'accroissement
1. Dans chacun des cas calculer le taux d'accroissement de la fonction affine $f.$
1. $f(1)=2$ et $f(3)=-2$
2. $f(2)=1$ et $f(5)=4$
3. $f(-5)=2$ et $f(6)=7$
4. $g(-1)=2$ et $g(-3)=5$
5. $f(-2)=6$ et $f(-2)=4$
6. $f(-2)=2$ et $f(6)=-2$
2. Sans dessin, dire pour chacun des couples de fonctions affines suivants laquelle a un graphe dont la pente est la plus forte :
a. $f\ :\ x\mapsto\,3x+2$ et $g\ :\ x\mapsto\,5x+7$
b. $l\ :\ x\mapsto\,-8x+2$ et $q\ :\ x\mapsto\,3x+9$
Exercice 5:
Détermination d'une application affine
1. Déterminer l'application affine $g$ telle que : $g(3)=-1$ et $g(-6)=5$
2. Déterminer l'application affine h telle que :
$h(-3)=6$ et $g(-1)=3$
3. Déterminer l'application affine $h$ telle que :
$h$ a pour coefficient directeur $-3$ et dont la représentation graphique est une droite qui passe par $A(-5\ ;\ 1)$
4. Déterminer l'application affine $p$ telle que :
$p$ a pour coefficient directeur $2$ et dont la représentation graphique est une droite qui passe par $M(2\ ;\ 3)$
Exercice 6:
Application affine par morceaux
Représenter graphiquement $f$ dans un repère orthonormé $\left(O\;,\ I\;\ J\right)$ définie par :
$f(x)=x+2$ si $x\in]-\infty\ ;\ -2]$
$f(x)=3x+1$ si $x\in[2\ ;\ 3[$
$f(x)=-x+2$ si $x\in]3\ ;\ +\infty[$
Exercice 7:
Application affine par morceaux
On considère la représentation graphique ci-dessous
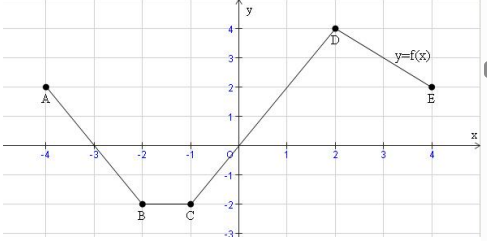
1. Déterminer graphiquement les coordonnées des points : $A$, $B$, $C$, $D$ et $E$
2. Déterminer les images des nombres : $-3$ ; $-1$ ; $1$ ; $2$ et $4$
3. Déterminer les antécédents des nombres : $-2$ ; $2$ et $3$
4. Déterminer la fonction affine par morceaux de cette représentation graphique.
Exercice 8:
Repérage
Le plan est muni d'un repère orthonormé $\left(O\;,\vec{i}\;,\vec{j}\right)$
On donne les points $A(8\;\ -4)$ ; $B(-7\ ;\ 5)$ , et $C=(-2\ ;\ -3)$
1. Place les points $A$ ; $B$ et $C$ dans ce repère.
2. Trouve une équation générale des droites $(AB)$ ; $(BC)$ et $(AC)$
3. Trouve le coefficient directeur de chacune des droites $(AB)$ ; $(BC)$ et $(AC)$
4. Trouve une équation de la droite $(d)$ passant par $M(1\ ;\ 2)$ et parallèle à $(AB)$
5. Trouve une équation de la droite $(d')$ passant par $N(-1\ ;\ -2)$ et perpendiculaire à $(BC)$
Exercice 9:
Dans le plan muni d'un repère orthonormé $\left(O\ ;\ OI\ ;\ OJ\right)$, on donne les droites $(D)$ et $(D')$ telles que :
$(D)\ :\ x-y+1=0$ et $(D')\ :\ x+y+3=0$
1. Montrer que les droites $(D)$ et $(D')$ sont perpendiculaires.
2. Tracer les droites $(D)$ et $(D')$ dans le repère.
3. Déterminer graphiquement les coordonnées du point d'intersection $A$ de $(D)$ et $(D')$.
Exercice 10:
Dans le plan muni d'un repère orthonormé $\left(O\ ;\ OI\ ;\ OJ\right)$, on donne les droites $(D)$ et $(D')$ telles que :
$\left(D_{1}\right)\ :\ y=x$ et $\left(D_{2}\right)\ :\ x+2$
1. Montrer que les droites $(D)$ et $(D')$ sont parallèles.
2. Tracer les droites $\left(D_{1}\right)$ et $\left(D_{2}\right)$ dans le repère.
Exercice 11
Dans le plan muni d'un repère orthonormal $\left(O\ ;\ I\ ;\ J\right)$, on considère les droites $\left(D_{1}\right)\ :\ -x+1$ et $\left(D_{2}\right)\ :\ x-y+3=0$
1. Démontre que les droites $\left(D_{1}\right)$ et $\left(D_{2}\right)$ sont perpendiculaires puis construis les droites $\left(D_{1}\right)$ et $\left(D_{2}\right)$
1. Justifie par le calcul que le point $J$ appartient à la droite $\left(D_{1}\right)$
2. On appelle $E$ le point d'intersection de $\left(D_{1}\right)$ et $\left(D_{2}\right)$
Justifie par le calcul que $E$ a pour couple de coordonnées $\left(-1\ ;\ 2\right)$
3. Calcule la distance $EJ$
Soient les fonctions $f\ :\ x\mapsto\,3x-1$ et $g\ :\ x\mapsto\,-x+3$ et les points $A(0\ ;\ -1)$ ; $B\left(\dfrac{1}{2}\ ;\ \dfrac{5}{2}\right)$ ; $C(-2\ ;\ 5)$ et $D(-2\ ;\ -7)$
1. Parmi les points $A$, $B$, $C$ et $D$, dire lesquels sont sur la représentation graphique de $g.$
2. Parmi les points $A$, $B$, $C$ et $D$, dire lesquels sont sur la représentation graphique de $f$
3. Trace les représentations graphiques de $f$et $g.$
4. Résoudre graphiquement ou algébriquement l'équation $f(x)=g(x)$
5. Donne les coordonnées du point d'intersection de la représentation graphique de $f$ et $g.$
6. Quelle est la position relative des représentations graphiques de $f$ et $g$ ?

Commentaires
Anonyme (non vérifié)
lun, 03/03/2025 - 21:25
Permalien
Ok
Ajouter un commentaire