Série d'exercices : Introduction à la géométrie - le plan et ses parties 6e
Classe:
Sixième
Exercice 1
Donner un objet qui à la forme :
$-\ $ D'un parallélépipède rectangle
$-\ $ D'un cube.
$-\ $ D'un cylindre
$-\ $ D'une sphère.
Exercice 2
1) Marquer deux points $A\ $ et $\ C$ puis tracer la droite $(AC)$ avec la règle.
2) Marque le point $M$ tel que $M$ n'appartient pas à la droite $(AC).$
3) Tracer les droites $(AM)\ $ et $\ (CM).$
4) Nommer les demi-droites d'extrémité $M.$
5) Nommer tous les segments.
Exercice 3
On considère la figure ci-dessous.
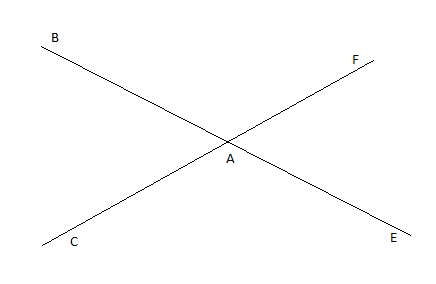
1) Reproduire la figure.
2) Compléter les pointillés par $\in$ ou $\notin .$
$A\ldots(BE)\;;\quad A\ldots(CE)\;;\quad B\ldots(AC)\;;\quad B\ldots(AE)$
3) Que peux-tu dire du point $A$ ?
4) Tracer les droites $(BC)\ $ et $\ (EF).$
Exercice 4
1) Marquer les points $A\;,\ B\ $ et $\ E$ sur une droite $(d).$
2) a) Donner deux autres noms de la droite $(d).$
b) Nommer les demi-droites d'origine $B.$
3) Nommer tous les segments qui sont sur la figure.
Exercice 5
1) Marquer les points $A\;,\ B\ $ et $\ E$ sur une droite $(d).$
2) Marque un point $F$ tel que : $F\notin\;(d).$
3) Tracer les droites $(AF)\;,\ (BF)\ $ et $\ (EF).$
4) Déterminer les points d'intersections des droites
a) $(AF)\ $ et $\ (EF)$
b) $(BF)\ $ et $\ (AE)$
5) Nommer tous les segments
Exercice 6
1) Construire quatre points alignés $M\;,\ N\;,\ P\ $ et $\ Q$ sur une droite $(d)$ dans cet ordre.
2) Nommer trois autres noms de la droite $(d).$
3) Nommer toutes les demi-droites d'origine $P.$
4) Nommer quatre segments dans cette figure.
Exercice 7
Construire une droite $(xy).$
1) Placer les points $A\;,\ B\;,\ C\ $ et $\ D$ sur la droite $(xy).$
2) Nommer toutes les demi-droites d'origine $C.$
3) Nommer toutes les demi-droites d'origine $B.$
Exercice 8
1) Placer les points $A\;,\ B\;,\ C\ $ et $\ E$ appartenant à une droite $(D)$ et le point $F$ n'appartient pas à cette droite $(D).$
2) Quels les points d'intersections des droites :
a) $(AC)\ $ et $\ (CF)$ ?
b) $(AE)\ $ et $\ (CF)$ ?
c) $(CE)\ $ et $\ (BF)$ ?
d) $(CF)\ $ et $\ (BF)$ ?
Exercice 9
Marque cinq points $B\;,\ E\;,\ H\;,\ M\ $ et $\ T$ tels que :
1) $H\;,\ T\ $ et $\ B$ soient alignés.
2) $B\;,\ M\ $ et $\ T$ soient non-alignés.
3) $E\;,\ T\ $ et $\ M$ soient alignés.
Exercice 10
On considère la figure ci-dessous.
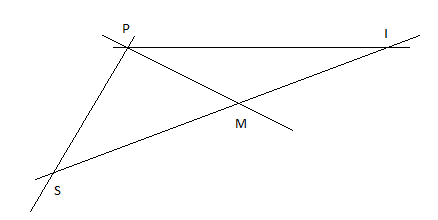
1) Recopier les phrases ci-dessous, puis complète par $\in$ ou $\notin$
$$S\ldots[IM)\;;\quad S\ldots[MI)\;;\quad S\ldots[MI]\;;\quad S\ldots(MI)$$
2) Combien de segments peux-tu nommer sur la figure ?
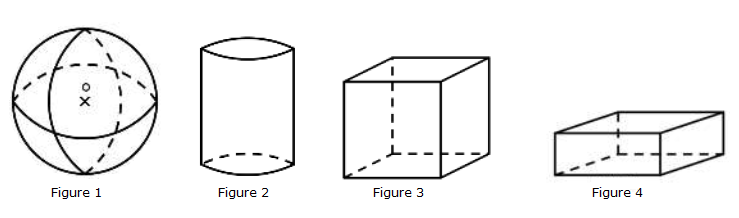
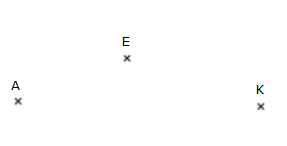


Exercice 11
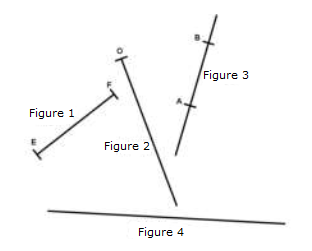
Donne le nom de chacune des figures ci-dessous :

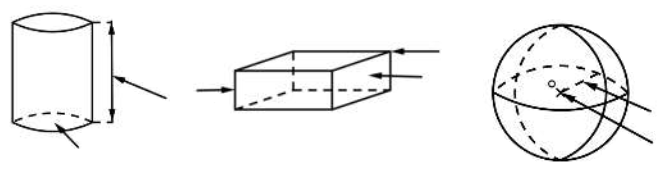
Exercice 12
Reproduis chacune des figures ci-dessous dans ton cahier, puis écris pour chaque flèche le nom correspondant à la partie désignée.

Exercice 13
Pour chaque énoncé, écris le numéro puis choisis la bonne réponse.
$$\begin{array}{|l|c|c|c|}\hline\qquad\qquad\text{Enoncés}&\text{Réponse A}&\text{Réponse B}&\text{Réponse C}\\\hline\text{1. Le nombre d'arêtes}&6&8&12\\\quad \text{d'un parallélépipède est}&&&\\\hline\text{2. Le nombre de sommets}&6&8&12\\\quad \text{d'un cube est}&&&\\\hline\text{3. Le nombre de faces}&6&8&12\\\quad \text{d'un parallélépipède est}&&&\\\hline\text{4. Un parallélépipède a pour face}&\text{un carré}&\text{un losange}&\text{un rectangle}\\\hline\end{array}$$
Exercice 14
On donne les figures ci-dessous. Pour chaque figure, recopie le numéro et indique s'il s'agit d'une droite, d'une demi-droite ou d'un segment.

Exercice 15
Recopie puis complète les phrases ci-dessous avec les mots :
droite, demi-droite, segment, origine, extrémités ou points.
$[AB]$ est un(e) $\ldots\ldots\ldots$ ; les $\ldots\ldots\ldots A\ $ et $\ B$ sont ses $\ldots\ldots\ldots$
$(CD)$ est un(e) $\ldots\ldots\ldots$ ; elle passe par les $\ldots\ldots\ldots C\ $ et $\ D.$
$[EF)$ est un(e) $\ldots\ldots\ldots$ ; le point $E$ est son $\ldots\ldots\ldots$
Exercice 16
1) Par un point donné, combien passe t-il de droites ?
2) Par deux points distincts, combien passe t-il de droites ?
Exercice 17
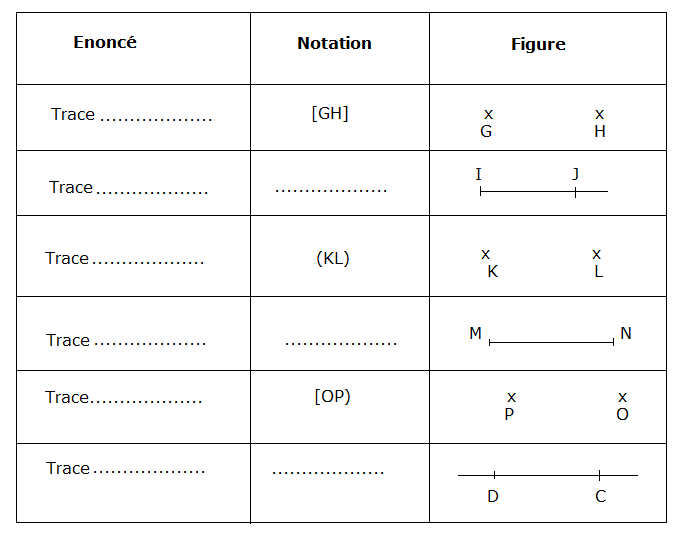
1) Reproduis puis complète le tableau suivant :
$$\begin{array}{|l|c|c|}\hline\qquad\qquad\qquad\text{Enoncés}&\text{Notation}&\text{Figure}\\\hline\text{Trace la droite passant par A et B}&&\\\hline\text{Trace le segment d’extrémités C et D}&&\\\hline\text{Trace la demi-droite d’origine A passant par F}&&\\\hline\end{array}$$
2) Reproduis puis complète le tableau suivant

Exercice 18
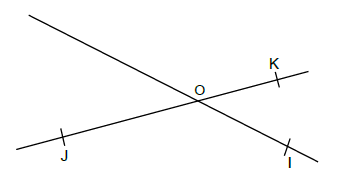
Reproduis la figure ci-dessous puis trace $(EA)\;,\ [EK]\ $ et $\ [AK).$
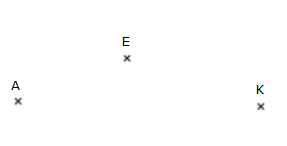
Exercice 19
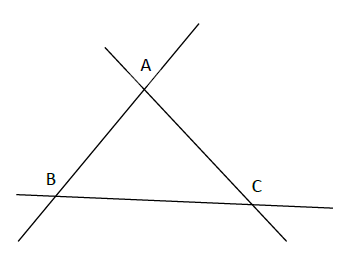
Reproduis la figure ci-dessous dans ton cahier et repasse au crayon :
1) la demi- droite $[AB)$ en rouge ;
2) la droite $(AC)$ en bleu ;
3) le segment $[BC]$ en jaune.

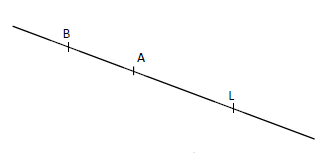
Exercice 20
Sur la figure ci-dessous, les points $A\;,\ B\ $ et $\ L$ sont alignés.
Écris tous les noms possibles :
1) de la droite ;
2) de la demi-droite d'origine $L$ passant par $B$ ;
3) de la demi-droite d'origine $A$ passant par $L$ ;
4) du segment d'extrémités $B\ $ et $\ L.$

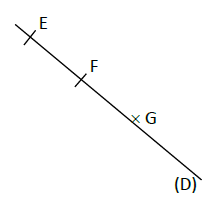
Exercice 21
On considère la figure ci- dessous, cite les points qui sont sur la droite $(D).$

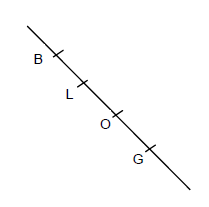
Exercice 22
On considère la figure ci-dessous. Les points $B\;,\ L\;,\ O\ $ et $\ G$ sont alignés.
Recopie et complète par $\in$ ou par $\notin$
$O\ldots\ldots[BG]\quad O\ldots\ldots[BL]\quad O\ldots\ldots[GL]$
$G\ldots\ldots[LO)\quad G\ldots\ldots[OL)\quad G\ldots\ldots[BL)$
$L\ldots\ldots[GO)\quad L\ldots\ldots[GO]\quad G\ldots\ldots(LO)$

Exercice 23
1) Place trois points $E\;,\ F\ $ et $\ G$ non alignés.
2. a) Trace le segment $[EF]$ en rouge.
b) Trace la demi-droite $[FG)$ en bleu.
c) Trace la droite $(EG)$ en vert.
3) Place un point $A$ tel que $A\in[EF].$
4) Place un point $B$ tel que $B\in[FG)\;,\ B\notin [FG].$
5) Place un $C$ point tels que $C\in(EG)\;,\ C\notin[EG).$
Exercice 24
1) Place quatre points $E\;,\ F\;,\ G\ $ et $\ H$ tels que :
$\centerdot\ E\;,\ F\ $ et $\ G$ soient alignés dans cet ordre ;
$\centerdot\ E\;,\ F\ $ et $\ H$ ne soient pas alignés.
2) En utilisant les symboles $\in$ ou $\notin$ recopie et complète
$E\ldots\ldots(FG)\quad E\ldots\ldots[EF]\quad E\ldots\ldots[FG]\quad E\ldots\ldots[EG)$
$F\ldots\ldots[EG)\quad H\ldots\ldots(FG)\quad H\ldots\ldots[FH]\quad G\ldots\ldots[FG).$
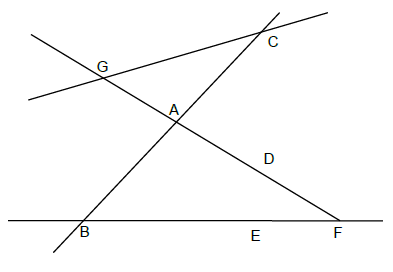
Exercice 25
On donne la figure ci-dessous

1) Remplace les pointillés par $\in$ ou $\notin$
$A\ldots\ldots(xy)\quad B\ldots\ldots(AE)\quad E\ldots\ldots(AB)\quad A\ldots\ldots(AB)$
$B\ldots\ldots[AE)\quad E\ldots\ldots[CB]\quad A\ldots\ldots[CB]\quad B\ldots\ldots[CE)$
$A\ldots\ldots[EB)\quad C\ldots\ldots[EA]\quad H\ldots\ldots(D)$
2) Donne trois noms de la droite $(xy).$
3) Donne tous les noms de la demi- droite $[BE).$
Exercice 26
Reproduis la figure ci-dessous puis trace en bleu les parties suivantes :
$[AG]\;,\ [DE)\;,\ (BA)\;,\ [GC)\;,\ (BE).$

Exercice 27
1) Reproduis la figure ci-dessous
2. a) Marque un point $L$ tel que $O\;,\ I\ $ et $\ L$ soient alignés ;
b) Marque un point $M$ tel que $O\;,\ J\ $ et $\ M$ soient alignés ;
c) Marque un point $P$ tel que $I\;,\ J\ $ et $\ P$ soient alignés ;
d) Marque un point $N$ tel que $I\;,\ K\ $ et $\ N$ soient alignés.
3) Recopie et remplace les pointillés par un nom de droite qui convient :
$L\in\ldots\ldots\quad M\in\ldots\ldots\quad N\in\ldots\ldots\quad P\in\ldots\ldots$

Exercice 28
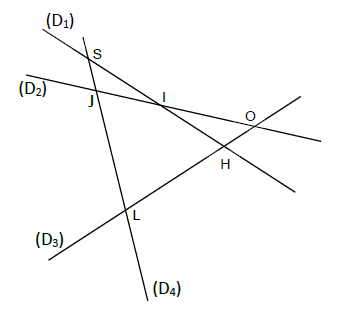
A l'aide de la figure ci-dessous complète :
$-\ $ les droite $(D_{1})\ $ et $\ (D_{2})$ se coupent en $\ldots\ldots$
$-\ \ I$ est le point d'intersection des droites $\ldots\ldots$ et $\ldots\ldots$
$-\ $ les droites $(IJ)\ $ et $\ (OL)$ sont sécantes en $\ldots\ldots$
$-\ $ les droites $(D_{4})\ $ et $\ (OH)$ se coupent en $\ldots\ldots$
$-\ \ldots\ldots$ est le point d'intersection des droites $(LH)\ $ et $\ (SI)$

Exercice 29
Reproduis la figure ci-dessous.
$A$ est le point d'intersection de $(D_{1})\ $ et $\ (D_{2}).$
Les droites $(D_{2})\ $ et $\ (D_{3})$ se coupent en $B.$
Les droites $(D_{4})\ $ et $\ (D_{3})$ se coupent en $C.$
Les droites $(D_{4})\ $ et $\ (D_{5})$ se coupent en $E.$
Place les points $A\;,\ B\;,\ C\ $ et $\ E.$

Exercice 30
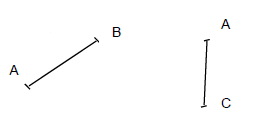
Un professeur de mathématique de sixième demande à ses élèves de tracer sur une même figure un segment d'extrémités $A\ $ et $\ B$ et un autre segment d'extrémités $A\ $ et $\ C.$
Voici la copie de l'élève

Quelle erreur a commise cet élève ?
Exercice 31
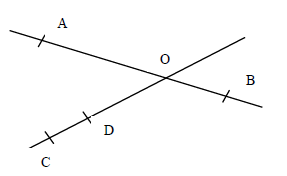
En te basant sur la figure ci-dessous réponds par vrai ou faux :

1) les points $A\;,\ O\ $ et $\ D$ sont alignés ;
2) $O\in[AB]$ ;
3) $O\in[DC]$ ;
4) les segments $[AB]\ $ et $\ [CD]$ n'ont pas de point en commun ;
5) les droites $(AB)\ $ et $\ (CD)$ sont sécantes en $O.$
Exercice 32
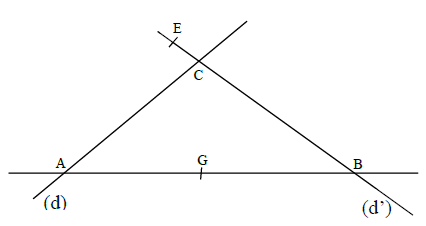
En utilisant les lettres de la figure ci-dessous, nomme de trois autres façons
1) la droite $(d)$ ;
2) la droite $(d').$

Exercice 33
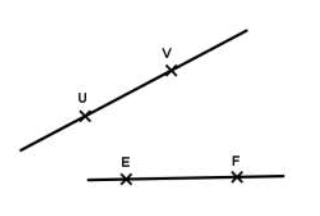
On considère la figure ci-dessous

Fatou dit les droites $(UV)\ $ et $\ (EF)$ ne sont pas sécantes.
A-t-elle raison ? Justifie.
Reproduis cette figure et place :
$-\ $ le point $C$ commun aux droites $(EU)\ $ et $\ (FV)$ ;
$-\ $ le point d'intersection $O$ des droites $(UF)\ $ et $\ (VE).$
$\begin{array}{c}\blacktriangleright\,\boxed{\text{Correction des exercices}}\end{array}$
Auteur:
Diny Faye & adem

Commentaires
Anonyme (non vérifié)
lun, 12/12/2022 - 10:50
Permalien
Série d'exercices très
Anonyme (non vérifié)
lun, 12/12/2022 - 10:51
Permalien
Dommage que ce n'est pas
Ajouter un commentaire