Déterminer l'ensemble de définition d'une fonction
Exercice 1
Déterminer l'ensemble de définition $f$ dans chacun des cas suivants :
1) $f\ :\ \mapsto\sqrt{x^{2}+2x+3}-\sqrt{x^{2}-3x-4}$
2) $f\ :\ x\mapsto\left\lbrace\begin{array}{ll} x+\dfrac{2}{\sqrt{x+4}}&\text{si }x\leq 0\\ \\ x+3-\sqrt{x^{2}+x-2}&\text{si }x>0 \end{array}\right.$
3) $f\ :\ x\mapsto\sqrt{\dfrac{1-3x}{x^{2}+5x}}$
4) $f\ :\ x\mapsto\dfrac{\sqrt{1+3x}}{\sqrt{x^{2}+5x}}$
5) $f\ :\ x\mapsto\dfrac{1}{\sqrt{x^{3}-12x}+16}$
6) $f\ :\ x\mapsto\dfrac{\sqrt{1-x}sq}{|x-3|-5}$
7) $f\ :\ x\mapsto\dfrac{1-\sqrt{x}}{\sin\pi x}$
8) $f\ :\ x\mapsto\dfrac{\tan x}{\sin(x^{2}-\pi^{2})}$
9) $f\ :\ x\mapsto\dfrac{\sqrt{2\sin x-1}}{2\sin^{2}x-1}$
Calculs de limites
Exercice 2
limite d'une fonction en $x_{0}$
Justifier les limites suivantes (en utilisant les limites de références du cours et les théorèmes sur les opérations sur les limites finies) :
$1)\ \lim_{x\rightarrow 1}(x^{3}-3x+5)=3\quad 2)\ \lim_{x\rightarrow -1}(2x^{2}+x-2)=-1\quad 3)\ \lim_{x\rightarrow 2}\dfrac{3x+1}{x-3}=-7$
$4)\ \lim_{x\rightarrow 3}\dfrac{x-1}{x^{2}+1}=\dfrac{1}{5}\quad 5)\ \lim_{x\rightarrow 1}\dfrac{2x^{2}+x-7}{x^{2}+3}=-1\quad 6)\ \lim_{x\rightarrow \dfrac{\pi}{6}}(3\sin x+1)=\dfrac{5}{2}\quad 7)\ \lim_{x\rightarrow 5}\sqrt{x-1}=2$
Extension de la notion de limite
Exercice 3
1) Déterminer la limite pour $x\mapsto+\infty$, et pour $x\mapsto -\infty$, de la fonction $f$, dans les cas suivants :
$\text{a) }f\ :\ x\mapsto x^{2}-3x+1\quad \text{b) }f\ :\ x\mapsto(x^{3}-x)(x+1)\quad \text{c) }f\ :\ x\mapsto x^{2}+|x-3|$
$\text{d) }f\ :\ x\mapsto 2x^{2}-|5x+4|\quad \text{e) }f\ :\ x\mapsto\dfrac{2x^{2}-x}{x+3}\quad \text{f) }f\ :\ x\mapsto\dfrac{x+1}{x^{2}+2}$
$\text{g) }f\ :\ x\mapsto\dfrac{x^{3}-3x}{x^{3}+x+2}\qquad \text{h) }f\ :\ x\mapsto\dfrac{\sqrt{x}+1}{\sqrt{x}-1}$
2) Déterminer la limite quand $x\mapsto x_{0}$ de la fonction $f$ dans les cas suivants :
$\text{a) }f\ :\ x\mapsto\dfrac{1}{x-1}\;,\ x_{0}=1\qquad \text{b) }f\ :\ x\mapsto\dfrac{-3}{x^{2}-4}\;,\ x_{0}=-2\text{ et }x_{0}=2$
$\text{c) }f\ :\ x\mapsto\dfrac{x^{2}+x+3}{(x+3)^{2}(x-2)}\;,\ x_{0}=-3\text{ et }x_{0}=2\quad \text{d) }f\ :\ x\mapsto\tan x\;,\ x_{0}=(2k+1)\dfrac{\pi}{2}$
$\text{e) }f\ :\ x\mapsto\dfrac{2}{1+\cos x}\;,\ x_{0}=\pi\qquad \text{f) }f\ :\ x\mapsto\dfrac{3}{1+2\sin x}\;,\ x_{0}=-\dfrac{\pi}{6}$
Exercice 4
Levée d'indétermination
Déterminer les limites des fonctions suivantes :
$1)\ f\ :\ x\mapsto\dfrac{x^{3}+3x-4}{x-1}\text{ en }1\;,\ -\infty\;,\ +\infty\quad 2)\ f\ : x\mapsto\dfrac{x^{2}+4x+4}{x^{3}+8}\text{ en }-2\;,\ -\infty\;,\ +\infty$
$3)\ f\ :\ x\mapsto\sqrt{1+x^{2}}-x\text{ en }-\infty\;,\ +\infty\quad 4)\ f\ :\ x\mapsto\dfrac{\sqrt{3+x}-2x}{x-1}\text{ en }1\;,\ +\infty$
$5)\ f\ :\ x\mapsto\dfrac{x^{3}+6x+7}{3x^{2}-x-4}\text{ en }-1\;,\ -\infty\;,\ +\infty\quad 6)\ f\ :\ x\mapsto\sqrt{1+x}-x\text{ en }+\infty$
$7)\ f\ :\ x\mapsto\dfrac{\sqrt{x+3}-2}{x-1}\text{ en }1\;,\ +\infty\quad 8)\ f\ :\ x\mapsto\dfrac{\sqrt{x+1}-2\sqrt{x-2}}{x-3}\text{ en }3\;,\ +\infty$
$9)\ f\ :\ x\mapsto\dfrac{\sqrt{3x+2}-\sqrt{11x-6}}{x-\sqrt{x+3}+1}\text{ en }1\quad 10)\ f\ :\ x\mapsto\dfrac{\sqrt{x^{2}+x+3}-3}{x^{2}+x-6}\text{ en }2$
$11)\ f\ :\ x\mapsto x\sqrt{\dfrac{2x}{x+1}}-2x\text{ en }-\infty\;,\ +\infty\quad 12)\ f\ :\ x\mapsto\dfrac{\sqrt{x^{2}-1}+3x}{x}\text{ en }+\infty$
$13)\ f\ :\ x\mapsto\sqrt{x^{2}+4x+3}-x\text{ en }+\infty\quad 14)\ f\ :\ x\mapsto\sqrt{x^{2}+4x+3}-(x+2)\text{ en }+\infty$
$15)\ f\ :\ x\mapsto\sqrt{x^{2}+4x+3}+x\text{ en }-\infty\quad 16)\ f\ :\ x\mapsto\sqrt{x^{2}+4x+3}+x+2\text{ en }+\infty$
$17)\ f\ :\ x\mapsto\sqrt{2x^{2}-3x+1}-\sqrt{x^{2}+x-1}\text{ en }-\infty\;,\ +\infty$
$18)\ f\ :\ x\mapsto\sqrt{x^{2}-1}-\sqrt{x^{2}+x+1}\text{ en }-\infty\;,\ +\infty$
$19)\ f\ :\ x\mapsto x\left(\sqrt{x^{2}+1}-x\right)\text{ en }-\infty\;,\ +\infty\quad 20)\ f\ :\ x\mapsto\dfrac{3\sqrt{x-1}-2\sqrt{x+4}}{\sqrt{x^{2}-9}-2\sqrt{x-1}}\text{ en }+\infty$
Limite d'une fonction trigonométrique en 0
Exercice 5
Utiliser le résultat $\lim_{x\rightarrow 0}\dfrac{\sin x}{x}=1$ pour étudier la limite éventuelle en 0 des fonctions suivantes :
$1)\ f\ :\ x\mapsto\dfrac{\sin5x}{2x}\quad 2)\ f\ :\ x\mapsto\dfrac{x}{\sin3x}\quad 3)\ f\ :\ x\mapsto\dfrac{\sin5x}{\sin4x}\quad 4)\ f\ :\ x\mapsto\dfrac{\tan x}{x}\quad 5)\ f\ :\ \dfrac{\tan2x}{\sin x}$
$6)\ f\ :\ x\mapsto\dfrac{\sin x}{\sqrt{x}}\quad 7)\ f\ :\ x\mapsto\dfrac{1-\cos x}{x^{2}}\quad 8)\ f\ :\ x\mapsto\dfrac{\sin x-x}{\cos x-1}$
$9)\ f\ :\ x\mapsto\dfrac{\sin x-x}{\cos x-1}\quad 10)\ f\ :\ x\mapsto\dfrac{\sin x-\tan x}{3x^{3}}$
$11)\ f\ :\ x\mapsto\dfrac{\tan2x}{\sqrt{1-\cos x}}\quad 12)\ f\ : x\mapsto\dfrac{1-\cos x}{\sin^{2}\pi x}$
$13)\ f\ :\ x\mapsto\dfrac{\sqrt{1-cos4x}}{\sin5x}\quad 14)\ f\ :\ x\mapsto\dfrac{\cos^{2}x-\sqrt{\cos x}}{\sqrt{\cos x}-1}\quad 15)\ f\ :\ x\mapsto\dfrac{\sin(2x^{2}+x)}{x(x+1)}$
$16)\ f\ :\ x\mapsto\dfrac{\sqrt{1+\sin x}-\sqrt{1-\sin x}}{x}\quad 17)\ f\ :\ x\mapsto\dfrac{1-\cos x}{\tan^{2}x}$
$18)\ f\ :\ x\mapsto\dfrac{x(1-\cos x)}{\sin3x-3\sin x}\quad 19)\ f\ :\ x\mapsto\dfrac{2x-\sin x}{1-\cos x}\quad 20)\ f\ :\ x\mapsto\dfrac{x+\sin x+\sin2x}{x(x^{2}-1)}$
Limite d'une fonction trigonométrique en $x_{0}$
Exercice 6
Déterminer les limites éventuelles en $x_{0}$ des fonctions suivantes :
$1)\ f\ :\ x\mapsto\dfrac{\sin(2x-\pi)}{\tan(2x-\pi)}\;,\ x_{0}=\dfrac{\pi}{2}\qquad 2)\ f\ :\ x\mapsto\dfrac{\sin 6x}{2\cos x-\sqrt{3}}\;,\ x_{0}=\dfrac{\pi}{6}$
$3)\ f\ :\ x\mapsto\dfrac{\tan x}{\sin 2x-1}\;,\ x_{0}=\dfrac{\pi}{4}\qquad 4)\ f\ :\ x\mapsto\dfrac{\cos\left(\dfrac{\pi}{4}-x\right)-\tan x}{1-\sin\left(\dfrac{\pi}{4}+x\right)}\;,\ x_{0}=\dfrac{\pi}{4}$
$5)\ f\ :\ x\mapsto\dfrac{\sin x}{5\cos^{2}x+\sin^{2}x-4\cos x}\;,\ x_{0}=\dfrac{\pi}{3}\qquad 6)\ f\ :\ x\mapsto\dfrac{\sin\left(\dfrac{\pi}{6}-x\right)}{1-2\sin x}\;,\ x_{0}=\dfrac{\pi}{6}$
$7)\ f\ :\ x\mapsto\dfrac{\tan\left(x+\dfrac{\pi}{2}\right)}{\sin2x-2+2\sin x-2\cos x}\;,\ x_{0}=-\dfrac{\pi}{3}\quad 8)\ f\ :\ x\mapsto\dfrac{\sin x-\cos x}{x-\dfrac{\pi}{4}}\;,\ x_{0}=\dfrac{\pi}{6}$
$9)\ f\ :\ x\mapsto\dfrac{\sin x+\sqrt{3\cos x}}{-\sin2x+\sqrt{3\cos2x}}\;,\ x_{0}=-\dfrac{\pi}{3}\quad 10)\ f\ :\ x\mapsto\dfrac{\cos x-\sqrt{3\sin x}}{x-\dfrac{\pi}{6}}\;,\ x_{0}=\dfrac{\pi}{6}$
$11)\ f\ :\ x\mapsto\dfrac{1-\sin x-\cos x}{1-\sin x+\cos x}\;,\ x_{0}=\dfrac{\pi}{2}\qquad 12)\ f\ :\ x\mapsto\dfrac{\cos3x}{1-2\sin x}\;,\ x_{0}\dfrac{\pi}{3}$
$13)\ f\ :\ x\mapsto\dfrac{x\sin x-\dfrac{\pi}{2}}{\cos x}\;,\ x_{0}=\dfrac{\pi}{2}\qquad 14)\ f\ :\ x\mapsto\dfrac{\sin x(1-\sin x)}{\cos x}\;,\ x_{0}=\dfrac{\pi}{2}$
Déterminer une limite par lecture graphique
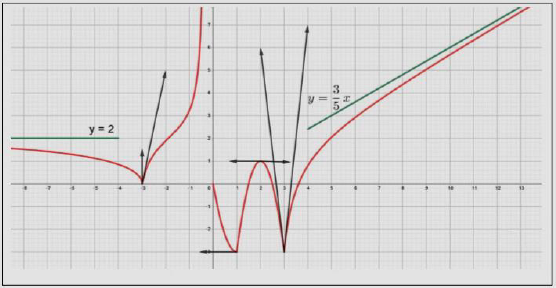
Exercice 7
La courbe $\mathcal{C}_{f}$ ci-dessous représente une fonction $f$ dans un repère orthonormé.
Déterminer graphiquement :
1) Le domaine de définition et de continuité de $f$
2) Les limites suivantes :
$\lim_{\,x\rightarrow 0^{-}}f(x)$ ;
$\lim_{\,x\rightarrow 0^{+}}f(x)$ ;
$\lim_{\,x\rightarrow +\infty}f(x)$ ;
$\lim_{\,x\rightarrow -\infty}f(x).$
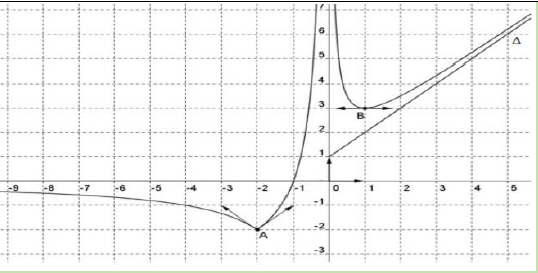
Exercice 8
Sur la figure ci-dessous, est tracée la courbe $\mathcal{C}_{f}$ représentative dans un repère orthonormé $(0\;,\ \vec{i}\;,\ \vec{j})$ d'une fonction $f$ continue sur $\mathbb{R}\setminus{0}.$
On sait de plus que :
$\ast$ La droite $\Delta$ est une asymptote à la courbe $\mathcal{C}_{f}$ au voisinage de $+\infty.$
$\ast$ La droite d'équation $y=0$ est une asymptote à la courbe $\mathcal{C}_{f}$ au voisinage de $-\infty.$
A partir du graphique et des renseignements fournis, déterminer les limites suivantes :
$\lim_{\,x\rightarrow +\infty}f(x)$ ;
$\lim_{\,x\rightarrow -\infty}f(x)$ ;
$\lim_{\,x\rightarrow 0^{-}}f(x)$ ;
$\lim_{\,x\rightarrow +\infty}\dfrac{f(x)}{x}.$
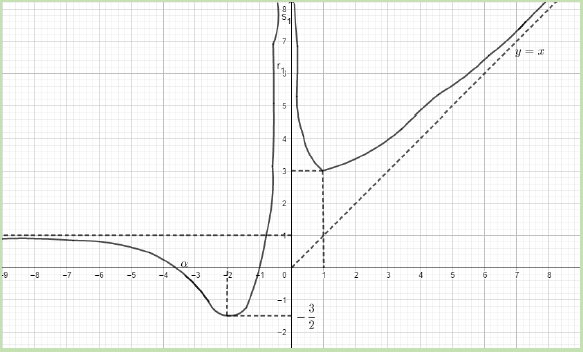
Exercice 9
La courbe ci-dessous est celle d'une fonction $f$ définie sur $\mathbb{R}^{\ast}$, la droite d'équation $y=x$ est une asymptote à la courbe au voisinage de $+\infty$, la droite d'équation : $y=1$ est une asymptote à la courbe au voisinage de $-\infty$ et l'axe des ordonnées est une asymptote verticale.
La courbe coupe l'axe des abscisses en deux points ,l'un d'eux est d'abscisse $-1$ et l'autre d'abscisse $\alpha.$
Déterminer les limites suivantes en utilisant le graphique :
a) $\lim_{\,x\rightarrow -\infty}f(x)\;;\quad\lim_{\,x\rightarrow +\infty}f(x)$ ;
b) $\lim_{\,x\rightarrow 0^{-}}f(x)\;;\quad\lim_{\,x\rightarrow 0^{+}}f(x)$
c) $\lim_{\,x\rightarrow +\infty}[f(x)-x]$
d) $\lim_{\,x\rightarrow\alpha^{-}}\dfrac{1}{f(x)}\;;\quad\lim_{\,x\rightarrow\alpha^{+}}\dfrac{1}{f(x)}$
Utilisation de la limite d'une fonction composée
Exercice 10
Déterminer les limites éventuelles des fonctions suivantes au point considéré :
$1)\ f\ :\ x\mapsto\cos\dfrac{\pi(x+1)}{x}\text{ en }+\infty\quad 2)\ f\ :\ x\mapsto\sqrt{\dfrac{2x^{2}-1}{x}}\text{ en }+\infty\quad 3)\ f\ :\ x\mapsto\sin\dfrac{1}{\sqrt{x}}\text{ en }+\infty$
$4)\ f\ :\ x\mapsto\dfrac{1-\sqrt{|x|}}{2+\sqrt{|x|}}\text{ en }-\infty\quad 5)\ f\ :\ x\mapsto \sqrt{\dfrac{2x+1}{x-3}}\text{ en }+\infty$
$6)\ f\ :\ x\mapsto\sqrt{\dfrac{2x+1}{x-3}}\text{ en }-\dfrac{1}{2}\;,\text{ puis en }3\quad 7)\ f\ :\ x\mapsto\sqrt{\dfrac{1}{x^{2}-1}}\text{ en }+\infty\;,\ -\infty\;,\ -1\;,\ 1$
$8)\ f\ :\ x\mapsto\sin\left(\dfrac{\pi x-1}{2x+1}\right)\text{ en }-\infty\;,\ +\infty\quad 9)\ f\ :\ x\mapsto\dfrac{2\cos^{3}x+3\cos x-5}{\sin^{2x}}\text{ en }0$
Utilisation des théorèmes de comparaison
Exercice 11
Déterminer la limite des fonctions suivantes :
$1)\ f\ :\ x\mapsto 1+x^{2}+\sin\dfrac{1}{x}\text{ en }x_{0}=0\qquad 2)\ f\ :\ x\mapsto\dfrac{\sin x}{x}\text{ en }+\infty\text{ et en }-\infty$
$3)\ f\ :\ x\mapsto\sin\dfrac{1}{x}+\dfrac{1}{x}\text{ en }x_{0}=0\qquad 4)\ f\ :\ x\mapsto\dfrac{\sin x+2}{x}\text{ en }+\infty\text{ et en }-\infty$
$5)\ f\ :\ x\mapsto\cos x-x\text{ en }+\infty\text{ et en }-\infty\qquad 6)\ f\ :\ x\mapsto1+x^{2}\sin\dfrac{1}{x}\text{ en }0$
$7)\ f\ :\ x\mapsto x\sin\dfrac{1}{x}-2\dfrac{\sin x}{x}\text{ en }+\infty\qquad 8)\ f\ :\ x\mapsto x\sin\dfrac{1}{x}\text{ en }0$
$9)\ f\ :\ x\mapsto x^{2}\cos\dfrac{1}{x}\text{ en }0\qquad 10)\ f\ :\ x\mapsto\dfrac{\sqrt{1+x^{2}}-1}{x}\sin\dfrac{1}{x}\text{ en }0$
$11)\ f\ :\ x\mapsto\dfrac{x-E(x)}{x}\text{ en }+\infty\text{ et en }-\infty\quad 12)\ f\ :\ x\mapsto\dfrac{x^{3}-5}{x^{4}+1}\sin2x^{2}\text{ en }+\infty\text{ et en }-\infty$
Étude des branches infinies
Exercice 12
Dans chacun des cas suivants, vérifier que les droites fixées sont asymptotes à la courbe $\mathcal{C}.$
1) $\mathcal{C}\ :\ y=\dfrac{x+2}{2x-3}\quad\mathcal{D}_{1}\ :\ x=\dfrac{3}{2}\quad\mathcal{D}_{2}\ :\ y=\dfrac{1}{2}$
2) $\mathcal{C}\ :\ y=\dfrac{2x-3}{3x-|x+1|}\quad\mathcal{D}_{1}\ :\ x=\dfrac{1}{2}\quad\mathcal{D}_{2}\ :\ y=\dfrac{1}{2}\quad\mathcal{D}_{3}\ :\ y=1$
3) $\mathcal{C}\ :\ y=\dfrac{x^{2}+1}{x-3}\quad\mathcal{D}_{1}\ :\ x=3\quad\mathcal{D}_{2}\ :\ y=x+3$
4) $\mathcal{C}\ :\ y=\dfrac{x^{3}+4x^{2}+3}{x^{2}+2x-1}\quad\mathcal{D}_{1}\ :\ x=-1-\sqrt{2}\quad\mathcal{D}_{2}\ :\ x=-1+\sqrt{2}\quad\mathcal{D}_{3}\ :\ y=x+2$
5) $\mathcal{C}\ :\ y=\sqrt{4x^{2}-3x+1}+x+\dfrac{1}{4}\quad\mathcal{D}_{1}\ :\ y=-x+1\quad\mathcal{D}_{2}\ :\ y=3x-\dfrac{1}{2}$
6) $\mathcal{C}\ :\ y=\sqrt{4x^{2}-3x+}-\sqrt{x^{2}+x}\quad\mathcal{D}_{1}\ :\ y=x-\dfrac{5}{4}\quad\mathcal{D}_{2}\ :\ x=-x+\dfrac{5}{4}$
Exercice 13
Soit $f$ la fonction définie sur $\mathbb{R}$ par :
$$f(x)=\left\lbrace\begin{array}{llll} \sqrt{x+2}&\text{si }x&\geq&-2\\ \\ \dfrac{2x^{2}-|x^{3}|}{x+2}&\text{si }x&<&-2 \end{array}\right.$$
1) Étudier la continuité de $f$ en $2.$
2) Étudier la continuité de $f$ sur $]-\infty\;;\ -2[$ et sur $[-2\;;\ +\infty[.$
3) La fonction $f$ est-elle continue sur $\mathbb{R}$ ?
Continuité et prolongement par continuité
Exercice 14
Déterminer l'ensemble de définition et étudier la continuité de la fonction $f$ dans chacun des cas suivants :
$1)\ f\ :\ x\mapsto3x^{2}+x-1\qquad 2)\ f\ :\ x\mapsto\dfrac{2x+1}{2x-1}\qquad 3)\ f\ :\ x\mapsto\sqrt{x^{2}+5x-5}$
$4)\ f\ :\ x\mapsto|2x+1|+|x-3|\quad 5)\ f\ :\ x\mapsto2x+1+\dfrac{\sqrt{x^{2}}}{x}\quad 6)\ f\ :\ x\mapsto 1+\dfrac{|x|}{x}$
$7)\ f\ :\ x\mapsto E(x)\quad 8)\ f\ :\ x\mapsto x-E(x)\quad 9)\ f\ :\ x\mapsto\left(x-E(x)\right)^{2}+E(x)$
$10)\ f\ :\ x\mapsto\sqrt{2x^{2}-|x+1|}\qquad 11)\ f\ :\ x\sqrt{x+\sqrt{1-x}}$
$12)\ f\ :\ x\mapsto\ \left\lbrace\begin{array}{lcl} -x&\text{ si }&x<0\\ x&\text{ si }&0\leq x\leq 1 \\ x^{2}&\text{ si }&x>1 \end{array}\right.$
Exercice 15
Limite à gauche, limite à droite
1) Montrer que, sur $\mathbb{R}^{\ast}$, on a $3\leq 4-\sin\dfrac{1}{x}\leq 5.$
2) Montrer que, sur $]0\;;\ 1[$, on a: $\dfrac{1}{x}\leq\dfrac{4-\sin\dfrac{1}{x}}{x}.$
3) Étudier la limite, à droite et à gauche, en 0, de la fonction $\text{f: }x\mapsto\dfrac{4-\sin\dfrac{1}{x}}{x}$
Limite à gauche, limite à droite
Exercice 16
Dans chacun des cas suivants, déterminer la limite à droite et à gauche en $x_{0}$ de la fonction $f.$
$1)\ f\ :\ x\mapsto\dfrac{1-\cos x}{x^{2}-2x|x|}\ x_{0}=0\quad 2)\ f\ :\ x\mapsto\ \left\lbrace\begin{array}{lcl} x^{2}-1\;,\ x &\leq & 0 \\ x^{2}+1\;,\ x &>& 0\ x_{0}=0\end{array}\right.$
$3)\ f\ :\ x\mapsto\dfrac{x^{2}+x}{\sqrt{x}^{2}}\ x_{0}=0\quad 4)\ f\ :\ x\mapsto\dfrac{|2x+1|}{2x+1}\ x_{0}=-\dfrac{1}{2}\quad 5)\ f\ :\ x\mapsto x\sqrt{(x-1)^{2}}\ x_{0}=1$
Exercice 17
On considère la fonction f définie par :
$$f(x)=\left\lbrace\begin{array}{lcl} x+1&\text{pour }&x\leq 1\\ 3-ax^{2}&\text{pour }&x>1 \end{array}\right.$$
Pour quelles valeurs de $a$ réel la fonction $f$ est-elle continue en $x_{0}=1$ ?
Exercice 18
Déterminer les réels $A\text{ et }B$ pour que la fonction $f$ soit continue en $\dfrac{\pi}{2}\text{ et }-\dfrac{\pi}{2}:$
$$f(x)=\left\lbrace\begin{array}{lcl} -2\sin x&\text{pour }&x \leq -\dfrac{\pi}{2} \\ \\ \text{A}\sin x+\text{B}&\text{pour }&-\dfrac{\pi}{2}<x<\dfrac{\pi}{2} \\ \\ \cos x&\text{pour }&x \geq\dfrac{\pi}{2} \end{array}\right.$$
Exercice 19
Montrer que la fonction $f$ définie par :
$$\left\lbrace\begin{array}{lllllll} f(x) &=& \dfrac{x^{3}-2x^{2}+x-2}{x-2}&\text{ pour }&x&<& 2 \\ \\ f(x) &=& 5\sin\dfrac{\pi x}{4} &\text{ pour }&x &\geq& 2 \end{array}\right.$$
est continue sur $\mathbb{R}$
Exercice 20
Montrer que les fonctions suivantes sont prolongeables par continuité en $x_{0}$ :
$1)\ f\ :\ x\mapsto\dfrac{x^{3}-x^{2}-2x+2}{x-1}\text{ en }x_{0}=1\quad 2)\ f\ :\ x\mapsto\dfrac{\sqrt{5x-1}-3}{x-2}\text{ en }x_{0}=2$
Exercice 21
1) Soit la fonction $f$ définie sur $[0\;;\ 1]$ par :
$$\left\lbrace\begin{array}{lllllll} f(x) &=& 6x^{2}+x+1 &\text{ pour }&x &\in &\left[0\;;\ \dfrac{1}{6}\right[ \\ \\ f(x) &=& \dfrac{6x+3}{2x+5} &\text{ pour }&x &\in&\left[\dfrac{1}{6}\;;\ 1\right[ \end{array}\right.$$
$f$ admet-elle une limite en $\dfrac{1}{6}$ ?
$f$ est-elle continue sur $[0\;;\ 1]$ ?
2) Soit $g\text{ et }h$ les fonctions numériques définies sur $[0\;;\ 1]$ par :
$$g(x)=\cos(3\pi x)\text{ et }h(x)=\cos(4\pi x).$$
Montrer que la fonction $f\,g$ est continue sur $[0\;;\ 1]$, mais qu'il n'en est pas de même pour la fonction $f\,h.$
3) Si on sait que le produit de deux fonctions est une fonction continue sur $[a\;;\ b]$, peut-on en déduire une conclusion quant à la continuité de chacune de ces fonctions ?
Exercice 22
Soit la fonction $f$ définie sur $\mathcal{R}$ par :
$$\left\lbrace\begin{array}{llllll} f(x) &=& 3x^{2}+ax+1\quad\text{pour }&x &<& 1\quad(a\in\mathcal{R}) \\ \\ f(x) &=& \dfrac{3x-1}{x+2}\quad\text{pour }&x &\geq & 1 \end{array}\right.$$
Déterminer $a$ pour que $f$ soit continue au point 1.
Exercice 23
Soit la fonction $f$ définie sur $\mathcal{R}\setminus \{1\}$ par :
$f(x)=\dfrac{3x^{2}+ax+1}{x-1}\quad(a\in\mathcal{R}).$
Déterminer $a$ pour que $f$ soit prolongeable par continuité au point 1. Définir alors la fonction $g$, prolongement par continuité de $f$ au point 1.
Exercice 24
Soit la fonction $f$ définie par :
$f(x)=\dfrac{\sqrt{x-a}-1}{x+1}$
Déterminer $a$ pour que $f$ soit prolongeable par continuité au point -1.
Définir alors la fonction $g$, prolongement par continuité de f au point -1.
Exercice 25
Soit $a$ un réel.
Déterminer, suivant les valeurs de $a$, les limites éventuelles respectives en $-\infty\;,\ +\infty\;,\text{ en }5$ de la fonction $f_{a}\ :\ x\mapsto\dfrac{a x^{2}+(a^{2}+1)x+a}{x-5}.$
Cette fonction admet-elle un prolongement par continuité au point 5 ?
Exercice 26
Soit $a$ un réel et $f_{a}$ la fonction :
$x\mapsto\dfrac{2x+x-3}{x^{2}+(1-a)x-a}$
1) Déterminer l'ensemble de définition de $f_{a}.$
2) Déterminer l'ensemble $E$ des réels $a$, pour chacun des quels $f_{a}$ admet un prolongement par continuité en $a.$
Pour chaque réel $a\text{ de }E$, déterminer le prolongement par continuité de $f_{a}\text{ en }a.$
Exercice 27
Soit la fonction $g$ définie par $g(x)=\dfrac{|x||x+1|}{(x+1)(x^{2}+x+1)}$
Peut-on définir un prolongement par continuité de $g$ au point -1 ?
Image d'un intervalle.Recherche de solutions d'équations
Exercice 28
Déterminer l'image de l'intervalle $I$ pour chacune des fonctions suivantes :
$1)\ f\ :\ x\mapsto\sin x\;,\text{ avec }I=\left[-\dfrac{\pi}{4}\;;\ \dfrac{\pi}{4}\right]\quad 2)\ f\ :\ x\mapsto\cos x\;,\text{ avec }I=\left[-\dfrac{\pi}{4}\;;\ \dfrac{\pi}{4}\right]$
$3)\ f\ :\ x\mapsto x^{3}-3x^{2}+1\;,\text{ avec }I=]-\infty\;;\ -1]$
$4)\ f\ :\ x\mapsto x^{3}-3x^{2}+1\;,\text{ avec }I=\left[\dfrac{1}{2}\;;\ 1\right]$
Exercice 29
Montrer que les fonctions suivantes sont bornées sur $I$ :
$1)\ f\ :\ x\mapsto\dfrac{1}{x^{2}+1}\text{ avec }I=\mathbb{R}\qquad 2)\ f\ :\ x\mapsto\dfrac{x-1}{x+1}\text{ avec }I=[2\;;\ +\infty[$
Exercice 30
Soit $f\ :\ [0\;;\ 6]\mapsto\mathbb{R}\quad x\mapsto|x^{2}-4x|$
1) Montrer que $f$ est continue sur $I=[0\;;\ 6].$
2) Étudier les variations de $f.$
Déterminer l'image de $I$ par $f.$
3) Soit $m$ un réel appartenant à l'intervalle $[f(0)\;;\ f(6)].$
Déterminer, suivant les valeurs de $m$, le nombre de solutions de l'équation $f(x)=m.$
Exercice 31
Soit $f\ :\ x\mapsto x^{2}-5x+10$
1) Montrer que $f$ est continue et strictement monotone sur $[-2\;;\ 2].$
2) $f$ est-elle strictement monotone sur $[0\;;\ 4]$ ?
3) Déterminer l'intervalle image par $f$ de $[0\;;\ 2 ].$
Exercice 32
Soit $f\ :\ \mathbb{R}\mapsto \mathbb{R}\quad x\mapsto\dfrac{2x+3}{x-2}$
1) Déterminer l'ensemble $D_{f}$ de définition de la fonction f puis l'ensemble image par f de $D_{f}$ (c'est-à dire $f(D_{f}).$
2) Montrer que $f$ est strictement monotone sur $]2\;;\ +\infty[.$
Quel est l'ensemble image par $f$ de $]2\;;\ +\infty[$ ?
3) Montrer que restriction $g$ de $f$ à $]2\;;\ +\infty[$ est une bijection de $]2\;;\ +\infty[$ sur lui-même.
Calculer alors $g^{-1}(x).$
Exercice 33
Soit f la fonction définie par :
$f(x)=x^{3}+5-100.$
1) Montrer que f est continue et strictement monotone sur $\mathbb{R}.$
2) Quel est image par f de l'intervalle $[0\;;\ 6]$ ?
3) Montrer que l'équation $f(x)=0$ admet une solution et une seule $\alpha$ comprise entre 0 et 6.
4) De plus, encadrer $\alpha$ entre deux entiers consécutifs.
Exercice 34
Soit f la fonction définie sur $[0\;;\ \pi[$ par :
$f(x)=\cos x-x.$
1) Montrer que f est une bijection de $[0\;;\ \pi[$ sur un ensemble $J$ que l'on précisera.
2) Montrer que l'équation $f(x)=0$ admet une solution et une seule $\gamma$ comprise entre 6 et 4.
Exercice 35
Dans chacun des cas suivants, justifier l'existence d'une unique solution $\alpha$ à l'équation $f(x)=0$ ; puis déterminer un encadrement à $10^{-2}$ près de $\alpha$
1) $f$ est définie sur $\mathbb{R}$ par :
$f\ :\ x\mapsto x^{3}+3x^{2}+1.x$
2) $f$ est définie sur $\mathbb{R}$ par :
$f\ :\ x\mapsto -x^{3}+3x^{2}+1.$
3) $f$ est définie sur $]-\pi\;;\ 0]$ par :
$f\ :\ x\mapsto x\sin x+\cos x.$
Exercice 36
Montrer que l'équation $x^{4}+4a x+b=0$ ($a\text{ et }b$ réels) ne peut avoir plus de deux solutions distinctes dans $\mathbb{R}.$
Exercice 37
Dans chacun des cas suivants, déterminer suivant les valeurs du paramètre réel $a$, le nombre de solutions de l'équation $f(x)=0$:
$1)\ f\ :\ x\mapsto x^{2}+a x+1\quad 2)\ f\ :\ x\mapsto x^{3}+3a x+1\quad 3)\ f\ :\ x\mapsto\cos x+a$
Exercice 38
Soit f la fonction définie sur $\mathbb{R}$ par :
$f(x)=x^{3}+x^{2}-x+1.$
Déterminer suivant les valeurs de $\lambda$, le nombre de solutions de l'équation $f(x)=\lambda.$
Propriétés des fonctions continues
Exercice 39
Soient $f\text{ et }g$ deux fonctions continues sur un intervalle $[a\;;\ b].$ On suppose que $f(a)=g(b)\text{ et }f(b)=g(a).$
Démontrer qu'il existe un réel $c$ de $[a\;;\ b]$ tel que $f(c)=g(c).$
Exercice 40
Soit f une fonction continue sur un intervalle $[a\;;\ b].$
Soient $p\text{ et }q$ des nombres réels strictement positifs.
Démontrer qu'il existe un réel $c$ de $[a\;;\ b]$ tel que :
$$f(c)=\dfrac{pf(a)+qf(b)}{p+q}.$$
Fonctions réciproques
Exercice 41
Dans chacun des cas suivants, établir que f est une bijection et déterminer la bijection réciproque $f^{-1}.$
$1)\ f\ :\ \mathbb{R}\mapsto\mathbb{R}\qquad 2)\ f\ :\ [0\;;\ 1]\rightarrow[-1\;;\ 0]\qquad 3)\ f\ :\ \mathbb{R}\setminus{1}\rightarrow\mathbb{R}^{\ast}$
$x\mapsto\dfrac{x}{1+|x|}\qquad x\mapsto x^{4}-2x^{2}\qquad x\mapsto\dfrac{x-1}{x}$
Exercice 42
1) La fonction $f\ :\ x\mapsto\sin x$ est continue sur $\mathbb{R}.$
Montrer que sa restriction à $[-\dfrac{\pi}{2}\;;\ \dfrac{\pi}{2}]$, considérée comme application de $[-\dfrac{\pi}{2}\;;\ \dfrac{\pi}{2}]\text{ vers }[-1\;;\ 1]$ admet une fonction réciproque.
Cette fonction réciproque sera notée $\arcsin.$
La fonction $f\ :\ x\mapsto\cos x$ est continue sur $\mathbb{R}.$
Montrer que sa restriction à $[0\;;\ \pi]$, considérée comme application de $[0\;;\ \pi]\text{ vers }[-1\;;\ 1]$ admet une fonction réciproque.
Cette fonction réciproque sera notée $\arccos.$
La fonction $f\ :\ x\mapsto\tan x$ est continue sur $]-\dfrac{\pi}{2}\;;\ \dfrac{\pi}{2}[.$
Montrer qu'elle admet sur cet intervalle une fonction réciproque. Cette fonction réciproque sera notée $\arctan.$
2) Préciser l'ensemble de définition et de continuité de chacune des fonctions $\arcsin\;,\ arccos\text{ et }arctan.$
Construire la courbe représentative de chacune d'elles.
Étudier la parité de ces fonctions.
3) Donner une expression simple de $\arcsin(\sin x)$, $\arccos(\cos x)$, $\arctan(\tan x).$
4) Donner une expression simple de $$\sin(\arcsin x)\;,\ \cos(\arccos x)\;,\ \tan(\arctan x)\;,\ \sin(\arccos x)\;,\ \cos(\arcsin x)$$
5) Montrer que, pour tout réel $x$ de l'intervalle $[-1\;;\ 1]$: $\arcsin x+\arccos x=2.$
Exercice 43
Calculer les limites suivantes des fonctions en $-\infty\text{ et }+\infty$
1) $f(x)=\dfrac{E(x)}{x-1} \;;\quad g(x)= xE(x) $ ;
$h(x) = \dfrac{xsin(x)}{x^2 -x+1}$
2) $f(x) =\sqrt{2x+1}-\sqrt{x}$ ;
$g(x)=\sqrt{x+1}-\sqrt{x}$ ;
$h(x)=\dfrac{\sqrt{x^2-1}+x}{x}$
Exercice 44
A) On définit la fonction $f_{m}$ par $f_{m}(x)=\sqrt{x^2+x+1}-mx$
1) Discuter suivant les valeurs du paramètre $m$ la limite en $+\infty$ et de $ - \infty$ de $f_{m}.$
2) Montre que $f_{0}$ admet des asymptotes dont on déterminera les équations et la position relative par rapport a la courbe de $f_{m}.$
B) On définit la fonction $g_{m}$ par :
$g_{m}(x)=\dfrac{(m^2-m)x^2+2mx+1}{(m-1)x^2+x-2}$
3) Discuter suivant les valeurs du paramètre $m$ la limite $g_{m}$ en $+\infty\text{ et }-\infty$
4) Montre que $g_{O}$ admet une asymptote dont on déterminera une équation
Exercice 45
1) Déterminer les limites aux bornes du domaine de définition de la fonction définie :
a) $f(x)=\dfrac{\sqrt{|x|}+\cos x}{x-\sin x}$ ;
b) $f(x)=\dfrac{\sqrt{x^2 +4x+3}}{2x}$ ;
$h(x)=\dfrac{\sqrt{x+2}-\sqrt{2x+1}}{x-1}$
Exercice 46
Soit une fonction vérifiant : $\lim_{x \to \infty} f(x) = +\infty$.
Étudier lorsque $x$ tend vers $+\infty$ la limite des fonctions suivantes :
a) $f(x)=\dfrac{3f(x)}{3+f(x)}$ ;
b) $h(x)= \dfrac{3f(x)}{3+(f(x))^2}$ ;
c) $i(x)=\dfrac{x+f(x)}{x}$
d) $j(x)=\dfrac{xf(x)}{x+f(x)}$ ;
e) $k(x)=\dfrac{x+f(x)}{x^2+f(x)}$ ;
f) $w(x)=\dfrac{3x-f(x)}{xf(x)}$
Exercice 47
Calculer les limites suivantes en utilisant la composition des fonctions
a) $\lim_{x\to +\infty}\cos\left[\left(\dfrac{x+1}{6x-\pi}\right)\pi\right]$ ;
b) $\lim_{x \to +\infty} \sqrt{\dfrac{2x^2}{x-1}}$
c) $\lim_{x \to 1}\tan \left[\left(\dfrac{x+1}{6x}\right)\dfrac{\pi}{2}\right]$
Exercice 48
Soit $g$ une fonction continue sur $\mathbb{R}$
1) Montrer que $|g|$ est continue sur $\mathbb{R}$
2) La réciproque est elle vraie ?
3) Donner un contre-exemple.
Exercice 49
1) Montrer que si une fonction continue sur un intervalle $I$ ne s'annule pas sur $I$, alors elle garde un signe constant sur cet intervalle.
2) Montrer que tous polynôme de degré impaire admet au moins une racine sur $\mathbb{R}$
3) Donner un exemple de polynômes de degré $2n(n\in\mathbb{N})$ qui ne s'annulent jamais sur $\mathbb{R}$
Exercice 50
1) Étudier les variations de la fonction définie $f\text{ sur }\mathbb{R}\text{ par : }f(x)=x^{3}-3ax+1$
En déduire suivant les valeurs de $a$ le nombre de solution de l'équation $f(x)=0$
2) Soit une fonction $f$ continue sur l'intervalle $[0\;;\ 1]$ à valeur dans $[0\;;\ 1]$ ; montrer que $f$ possède un point fixe c'est à dire qu'il existe un réel $\alpha$ tel que : $f(\alpha)=\alpha$.
Exercice 51
Calculer les limites suivantes en identifiant la limite demandée à un taux de variation
a) $\lim_{x\to +\dfrac{\pi}{6}}\dfrac{12\sin x-6}{6x-\pi}$ ;
b) $\lim_{x \to \dfrac{1}{3}}\dfrac{\sin 3\pi x}{1-2\cos \pi x}$ ;
c) $\lim_{x \to 4} \dfrac{\sqrt{x+5}-3}{x-4}$
d) $\lim_{x \to +\dfrac{\pi}{4}} \dfrac{\tan x -1}{4x-\pi}$ ;
e) $\lim_{x \to 0} \dfrac{12\sin x}{\pi x}$ ;
f) $\lim_{x \to 0} \dfrac{\sin 2x}{\sin \pi x}$
Exercice 52
1) soit la fonction $g: \to \begin{cases}\dfrac{1-\cos x}{x} & si \ x \neq 0 \\ 0 & si \ x = 0 \\ \end{cases}$
a) justifier la continuité de $f$ et montrer que $f$ est dérivable en $0$
b) calculer $f'(0).$
2) Donner pour chaque fonction la dérivée sur un ensemble que l'on précisera
a) $h(x)=x^2(2x-4)^2\;;\quad f(x)=x^3\sqrt{3x-1}$ ;
$g(x)=\dfrac{\sin x}{2x^2+1} \;;\quad q(x)=\dfrac{x}{\sqrt{2x+1}}$
b) $v(x)=\sqrt{\dfrac{x+2}{2x^2+4}}\;;\quad w(x)=\cos (x^2+1)$
$\sin^2 (3x+4\pi)$
Exercice 53
Soit $f$ la fonction définie par $f(x)=\dfrac{5+4x^2}{1+x^2}$ sur l'intervalle $]-1;+\infty[$
1) Montrer que $f$ est dérivable sur $]-1;+\infty[$
et calculer $f^\prime (x)$
2) soit $\phi$ la fonction définie par $\phi (x) =\dfrac{5+4\cos ^2x}{1+\cos ^2 x}$ sur l'intervalle $]-\pi;\pi[$
a) Écris $\phi$ comme la composée de deux fonctions dérivable et calculer $\phi ^\prime (x)$
b) Déduisez en le sens de variation de $\phi$ sur $]-\pi\;;\ \pi[$
Exercice 54
Soit $f$ la fonction définie sur $\mathbb{R}$ .
1) Montrer que $f$ est dérivable ; calculer $f^\prime$ et majorer $|f^\prime (x)|$ sur $\left[-\dfrac{\pi}{12}\;\ \dfrac{\pi}{12}\right]$
2) Montrer que quelque soit $f$ appartenant à $I$ ; $|\cos^2 x- \cos^2 y|\leq \dfrac{1}{2}|x-y|$
Exercice 55
Soit la fonction définie par $g(x)=\sqrt{x+1}$ sur l'intervalle $]-1;+\infty[$
1) Montrer que $g$ est dérivable sur $]-1;+\infty[$ et calculer $g^\prime (x)$ puis encadrer $g^\prime (x)\text{ sur }\left[0;\dfrac{1}{2}\right]$
2) Déduisez en que pour tout $x$ appartenant à $\left[0;\dfrac{1}{2}\right]$ on a : $1+\dfrac{x}{6}\leq g(x) \leq 1+\dfrac{x}{2}$.
Exercice 56
On admet qu'il existe une fonction $f$ dérivable qui vérifie sur $\mathbb{R}$ : $f^\prime (x)=\dfrac{1}{1+[ f(x) ]}$ dont la courbe représentative $(\mathcal{C})$ passe par l'origine $3$ du repère.
1) Déterminer une équation de la tangente $(T)$ à $(\mathcal{C})$ en $0.$
2) Montrer que $(\mathcal{C})$ n'admet pas une tangente parallèle à la droite $(\Delta)$ : $y=2x$
Justifier l'existence de la dérivée seconde $f''$ et montrer que $f''(x)=-2(f(x))^{3}f(x).$
Exercice 57
Soit une fonction définie et dérivable sur l'intervalle $[1;+\infty[$ vérifiant la relation : $$w(1)=0\text{ et }w^\prime (x)=\dfrac{1}{\sqrt{1+x^4}}$$
1) Étudier les variations de $f$ sur l'intervalle $[1;+\infty[$
2) On définie la fonction sur l'intervalle par $g(x)=1-\dfrac{1}{x}$
Comparer $w^\prime\text{ et }g^\prime\text{ puis }g\text{ et }w$ sur $[1;\;\ +\infty[$
3) Montrer alors que $w$ est majorée sur $[1;+\infty[$ et admet une limite $l$ en $+\infty$ ; vérifiant : $0\leq l \leq 1$
Exercice 58
Déterminer une primitive $F$ de la fonction sur intervalle I à préciser dans les cas suivants :
a) $f(x)=9x^4-\dfrac{1}{\sqrt{x}}$ ;
b) $f(x)=9x^2(4-x^3)^8$ ;
c) $f(x)=\dfrac{x^2}{\sqrt{x^3+2}}$ ;
d) $f(x)=\dfrac{1}{(2x+1)\sqrt{2x+1}}$ ;
e) $f(x)=\dfrac{x^4-x^3+3x^2+1}{x^2(x^2+1)^2}$
$\left(\text{trouver }a\text{ et }b f(x)=\dfrac{a}{x^2}+\dfrac{b}{(x^2+1)^2}\right)$
f) $f(x)=\dfrac{\sin x}{\cos^2 x}$ ;
g) $f(x)=\cos^3 x-\cos 2x$ ;
h) $f(x)=9\cos^4 x +\sin x\cos x$
Exercice 59
1) Trouver les primitives sur l'intervalle $]0\;;\ +\infty[$ de la fonction définie par : $f(x)=5x^2+\dfrac{2}{x^2}$
2) Déduisez en les primitives sur l'intervalle $]0\;;\ \pi[$ de la fonction définie par : $g(x)=5\sin^2 x \cos x+\dfrac{2\cos x}{\cos^3 x}$
3) Trouver la primitive vérifiant $g(0)=0$.
Exercice 60
Soit $f(x)\text{ et }w(x)$ deux fonctions définies sur l'intervalle $I=\left[\pi\;;\ \dfrac{\pi}{4}\right[$ par :
$f(x)=\dfrac{\sin x}{\cos^3 x}\text{ et }w(x)=\dfrac{1}{\cos^4 x}$
1) vérifier que $f^\prime (x)=\dfrac{3}{\cos^4 x}-\dfrac{2}{\cos^2 x}$
2) En déduire sur $I$ une primitive de la fonction $w.$
Exercice 61
Soit $f$ une fonction définie sur $\mathbb{R}$ par $f(x)=\dfrac{x^2+2x}{(x^2+x+1)^2}$
1) Montre que $f$ admet une primitive $F$ sur $\mathbb{R}$ de la forme $F(x)=\dfrac{ax+b}{x^2+x+1}$
2) Trouver toutes les primitives de $f$ sur $\mathbb{R}.$
Exercice 62
Soit $f$ une fonction définie dans $\mathbb{R}$ par $f(x)=\cos x-\dfrac{4}{3}\cos ^3 x$
1) Déterminer $f^\prime\text{ et }f''.$
Vérifier que pour tout $x$ de $\mathbb{R}$ ; $f''(x)=-9f(x)$
2) En déduire toutes les primitives de $f\text{ sur }\mathbb{R}$
3) Trouver les primitives sur $\mathbb{R}$ qui s'annule en $\dfrac{\pi}{6}.$

Commentaires
Anonyme (non vérifié)
ven, 10/23/2020 - 17:47
Permalien
merci pour votre effort;
لطفي معلاوي (non vérifié)
jeu, 09/15/2022 - 18:53
Permalien
Format
Pascal (non vérifié)
mar, 06/27/2023 - 11:54
Permalien
Sujets
Anonyme (non vérifié)
ven, 07/19/2024 - 02:49
Permalien
Très cool
Ajouter un commentaire