Série d'exercices sur le dénombrement 1e S

Soit:
 
$E=\{1\;,\ 2\;,\cdots\;,\ 8\;,\ 9\}\;,\qquad A=\{1\;,\ 2\;,\ 3\;,\ 4\}$

$B=\{2\;,\ 4\;,\ 6\;,\ 8\}\text{ et }C=\{3\;,\ 4\;,\ 5\;,\ 6\}.$

Déterminer :

(i) $\overline{A}\;,\quad$ (ii) $A\cap C\;,\quad$(iii) $\overline{A\cap C}$

(iv) $A\cup B\;,\quad$(v) $B\cap \overline{C}$

Soit :

$E=\{a\;,\ b\;,\ c\;,\ d\;,\ e\}\;,\qquad A=\{a\;,\ b\;,\ d\}\quad\text{et}\quad B=\{b\;,\ d\;,\ e\}$

Déterminer :

(i) $A\cup B\quad$(ii) $B\cap A\quad$(iii) $\overline{B}\quad$

(iv) $B\cup \overline{A}\quad$(v) $\overline{A}\cap B\quad$(vi) $A\cup \overline{B}$

(vii) $A\cap \overline{B}\quad$(viii) $\overline{A}\cap \overline{B}\quad$

(ix) $\overline{A\cup B}\quad$(x) $\overline{A}\cup \overline{B}\quad$(xi) $\overline{A\cap B}$

Dans un groupe de 20 camarades, 12 jouent au football et 11 jouent au basket, 4 jouent à la fois au football et au basket.

Dénombrer les élèves qui :

1) jouent seulement au football.

2) ne jouent ni au football ni au basket.

Dans une classe de 30 élèves, chaque élève étudie au moins une des trois langues : anglais, allemand, espagnol.

Un élève étudient les trois langues, 17 élèves étudient l'anglais, 8 étudient l'anglais et l'allemand, 5 étudient l'anglais et l'espagnol, 17 élèves étudient exactement 2 langues, 26 élèves étudient l'allemand ou l'anglais.

1) Combien d'élèves étudient l'allemand ?

2) Combien d'élèves étudient l'espagnol ?

3) Combien d'élèves étudient une seule langue ?

Parmi 40 personnes :

8 parlent le Poulaar, 15 le Diola et 8 le Sereer.

5 parlent le Poulaar et le Diola.

4 parlent le Diola et le Sereer

2 parlent le Poulaar et le Sereer.

2 parlent les trois langues.

1) Combien de personnes parlent au moins l'une des trois langues ?

2) Combien de secrétaires ne connaissent aucune de ces trois langues ?

Un certain produit se vend en liquide ou poudre.

Un sondage fait ressortir les faits suivants :

Le tiers des personnes interrogées n'utilise pas la poudre.

Les deux septièmes des personnes interrogées n'utilise pas le liquide.

427 personnes utilisent le liquide et la poudre.

Le cinquième des personnes interrogées n'utilise pas du tout le produit.

Combien de personnes ont été interrogées au cours de ce sondage ?

Dans un lycée de 800 élèves, il y a 60 enseignants et 30 personnels (administratifs et de service).

$60\%$ de l'ensemble des personnes travaillant dans le lycée(enseignants, élèves et personnels) sont des femmes.

Parmi les enseignants, $55\%$ sont des femmes, et parmi le personnel il y a 14 hommes.

1) Combien y-t-il de femmes dans l'ensemble des personnes travaillant dans le lycée ?

Combien y-t-il de femmes enseignantes ?

2) Représenter ces données dans un tableau à double entrée que l'on complètera.

3) Représenter ces données par un arbre que l'on complètera.

Soit :

$A=\{1\;,\ 2\;,\ 3\}\;,\quad B=\{2\;\ 4\}\quad\text{et}\quad C=\{3\;,\ 4\;,\ 5\}.$

Déterminer :

$A\times B\times C.$

On pourra utiliser un diagramme arborescent.

Soit :

$A=\{a\;,\ b\}\;,\quad B=\{2\;,\ 3\}\quad\text{et}\quad C=\{3\;,\ 4\}$

Déterminer :

(i) $A\times (B\cup C)\;,\quad$(ii) $(A\times B)\cup (A\times C)\;,\quad$(iii) $A\times(B\cap C)\;,\quad$

(iv) $(A\times B)\cap(A\times C)$

Déterminer le nombre d'éléments d'un ensemble $E$ dans les cas suivants :

1) Le nombre de couples de $E$ est 56.

2) Le nombre de triplets de $E$ est 120.

On joue avec deux dés. Le dé $n^{\circ}$ est cubique et ses 6 faces sont numérotées de 1 à 6.

Le dé $n^{\circ}$ est tétraédrique et ses 4 faces sont notées $A\;,\ B\;,\ C\;,\ D.$

Écrire dans un tableau tous les tirages possibles et les dénombrer.

Un établissement propose à ses élèves le choix de langues suivant :

Anglais $(A)$, Allemand $(D)$, Espagnol $(E)$, Italien $(I)$, Russe $(R)$.

Un élève doit choisir deux langues vivantes : LV1 et LV2.

1) En utilisant un diagramme en arbre, énumérer et dénombrer tous les choix possibles

(On remarquera qu'un élève ne peut pas choisir la mème langue en LV1 et LV2)

2) Même question pour le choix de trois langues LV1, LV2, LV3.

Un test d'aptitude consiste à poser à chaque candidat une série de quatre questions indépendantes auxquelles il doit répondre par Oui ou Non

Un candidat répond au hasard. En utilisant une disposition en forme d'arbre, déterminer combien de possibilités il a de répondre au questionnaire.

La figure suivante représente trois villes $A\;,\ B\text{ et }C$ ainsi que les routes qui les relient.

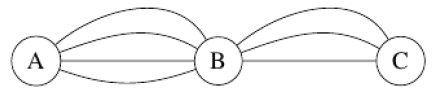
Déterminer :

1) le nombre d'itinéraires distincts menant de $A\text{ à }C$ ?

2) le nombre d'itinéraires aller retour $A-B-C-A$ n'empruntant que des chemins distincts ?

Un fabriquant de chaussures réalise trois modèles différents.

De plus, il peut faire chacun d'eux en trois couleurs et en quatre tailles différentes.

Combien de paires de chaussures distinctes peut-t-il proposer à sa clientèle ?

On veut choisir deux personnes de nationalités différentes parmi 5 camerounais, 10 malgaches et 6 sénégalais.

Combien y a t-il de possibilités ?

Combien de nombres peut-on former avec des chiffres distincts choisis parmi les éléments de
$E=\{1\;;\ 2\;;\ 3\;;\ 4\;;\ 5\}$ ?

En informatique on utilise le système binaire pour coder les caractères.

Un bit (binary digit : chiffre binaire) est un élément qui prend la valeur 0 ou la valeur 1.

Avec 8 chiffres binaires (un octet), combien de caractères peut-on coder ?

On jette six fois de suite un dé dont les faces sont numérotées de 1 à 6 et on note les résultats possibles.

1) Calculer le nombre de résultats possibles.

2) Calculer le nombre de façons d'obtenir :

a) le même numéro six fois ;

b) le numéro 5 exactement une fois.

c) le 6 suivi du numéro 5.

Une urne contient 3 boules vertes, 5 boules jaunes, 4 rouges et 2 noires.

On tire successivement avec remise 4 boules de l'urne.

Déterminer le nombre de tirages :

comportant :

1) a) 4 jaunes

b) 4 vertes

c) 4 boules de même couleur

d) 4 boules de couleurs distinctes deux à deux.

e) 3 jaunes et une verte dans cet ordre

f) 3 jaunes et une verte dans un ordre quelconque.

g) 2 jaunes et 2 vertes dans cet ordre

h) 2 jaunes et 2 vertes

2) Reprendre la question 1) dans le cas où les 4 boules sont tirées successivement sans remise.

Huit coureurs, 3 Sénégalais et 5 étrangers participent à une course et sont classés de 1 à 8.

1) Quel est le nombre d'arrivées possibles ?

2) Quel est le nombre d'arrivées lorsque la course est gagnée par un Sénégalais ?

3) Quel est le nombre de possibilités pour qu'il y ait un Sénégalais et un seul parmi les trois premiers coureurs ?

Un homme d'affaires doit se rendre dans quatre villes $A\;,\ B\;,\ C\text{ et }D.$

Combien de voyages différents peut-il réaliser sachant que :

1) il peut commencer et finir par la ville qu'il veut ?

2) il doit commencer par $D.$

3) il doit commencer par $D$ et finir par $A$ ?

Les numéros d'un réseau téléphonique sont tous formés de 9 chiffres choisis parmi les chiffres :

$0\;,\ 1\;,\ 2\;,\ 3\;,\ 4\;,\ 5\;,\ 6\;,\ 7\;,\ 8\;,\ 9.$

Exemples de numéros théoriquement acceptés :

$000 00 00\;;\ 961 52 87\;;\ 022 23 33\;;\ etc\cdots$

Calculer le cardinal des ensembles suivants :

$\Omega$ : la capacité théorique du réseau.

$A$ : ensemble des numéros composés de 9 chiffres distincts.

$B$ : ensemble des numéros composés de 9 chiffres identiques.

$C$ : ensemble des numéros ne contenant aucun chiffre 0.

$D$ : ensemble des numéros contenant exactement un 0.

$E$ : ensemble des numéros contenant au moins un 0.

$F$ : ensemble des numéros contenant au plus un 0.

$G$ : ensemble des numéros contenant au moins deux 0.

$H$ : ensemble des numéros pairs, chaque numéro étant strictement inférieur à 7000000.

$I$ : ensemble des numéros commençant par un chiffre pair et finissant par un chiffre impair strictement inférieur à 9.

Une classe de 30 élèves, 18 filles et 12 garçons, doit élire un comité comprenant un président, un trésorier et un secrétaire (sachant qu'il n y a ni cumul ni discrimination).

1) Combien de comités peut-on ainsi constituer ?

2) Quel est le nombre de comités comprenant l'élève $X$ ?

3) Quel est le nombre de comités pour lesquels le président est une fille et le secrétaire un garçon ?

4) Sachant que le président est un garçon, le secrétaire une fille, et que $M^{r}\;X$ ne veut pas faire partie du même comité que $M^{elle}\;Y$, quel est le nombre de comités possibles ?

Le code PIN d'un téléphone portable est un nombre de quatre chiffres choisis parmi

$0\;,\ 1\;,\ 2\;,\ 3\;,\ 4\;,\ 5\;,\ 6\;,\ 7\;,\ 8\text{ et }9.$

1) a) Quel est le nombre de codes possibles ?

b) Quel est le nombre de codes formés de quatre chiffres deux à deux distincts ?

2) Le téléphone portable étant éteint, le propriétaire voulant l'allumer sait que les quatre chiffres de ce code sont $1\;,\ 9\;,\ 8\text{ et }5$ mais il ignore l'ordre des chiffres.

a) Combien de codes différents peut-il composer avec ces 4 chiffres ?

b) Si le premier code introduit n'est pas bon, il doit attendre $2\;mn$ avant de pouvoir tenter un second essai ; le délai d'attente entre le second et le troisième essai est $4\;mn$ ; entre le $3^{eme}\text{ et }4^{eme}$ essai est de $8\;mn.$

(Le délai d'attente double entre deux essais successifs).

Combien de codes peut-il introduire au maximum en 24 h ?

Un étudiant possède 14 livres de quatre matières différentes :

4 livres de mathématiques, 5 d'économie, 5 de philosophie, 1 d'anglais.

Il veut ranger ces livres sur une étagère.

1) De combien de façon peut-il le faire s'il ne tient pas compte des matières ?

2) De combien de façons peut-il le faire s'il range d'abord les livres d'anglais, puis ceux d'économie, puis ceux de maths, et enfin ceux de philo ?

3) De combien de façons peut-il le faire s'il range les livres par matière ?

Un professeur dispose de 32 livres sur un rayon de sa bibliothèque.

23 d'entre eux sont des livres de mathématiques et 9 de physique.

Le professeur aimerait ranger ses livres de sorte que tous les livres traitant du même sujet restent groupés.

Combien y a t-il de dispositions possibles ?

4 sénégalais, 3 maliens et 5 gambiens doivent s'asseoir sur un même banc.

Les gens de même nationalité doivent rester ensemble.

Combien de dispositions peut-on imaginer ?

Une urne contient 5 jetons verts numérotés de 1 à 5 et 4 jetons rouges numérotés de 1 à 4

On tire simultanément 3 jetons de l'urne.

Combien y a t il de tirages contenant :

(a) 3 jetons de la même couleur ?

(b) contenant le vert numéro 1 et le rouge numéro 1 ?

(c) un seul jeton portant le numéro 1 ?

(d) exactement un jeton vert et un jeton numéro 1 ?

On considère un jeu classique de 32 cartes

On rappelle que celles-ci peuvent être de 4 couleurs (cœur, pique, trèfle, carreau) comportant chacune 8 valeurs

$(7\;,\ 8\;,\ 9\;,\ 10\;,\text{ Valet}\;,\text{ Dame}\;,\text{ Roi}\;,\text{ As})$

On tire simultanément 5 cartes dans un jeu de 32 cartes.

1) Dénombrer tous les tirages possibles.

2) Dénombrer les tirages comportant :

(a) 5 cartes de même couleur

(b) 4 cœurs et un pique

(c) 2 couleurs dont l'une revient 4 fois

(d) Exactement 4 trèfles et un roi.

On tire simultanément 3 boules d'une urne contenant 3 boules rouges 4 boules blanches et 4 boules noires

Déterminer le nombre de résultats possibles.

On note :

$A$ l'ensemble des résultats unicolores,

$B$ l'ensemble des résultats tricolores,

$C$ l'ensemble des résultats contenant 2 boules rouges et une boule noire,

$D$ l'ensemble des résultats contenant 2 boules rouges et une boule d'une autre couleur.

$E$ l'ensemble des résultats contenant 2 boules d'une même couleur et une boule d'une autre couleur.

1) Calculer

$\text{card}\;A\;,\ \text{card}\;B\;,\ \text{card}\;C\;,\ \text{card}\;D\text{ et }\text{card}\;E$

2) Soit $F$ l'ensemble des résultats contenant au moins une boule noire

Définir $F$ et calculer $\text{card}\;F$

En déduire $\text{card}\;F$

3) Soit $G$ l'ensemble des résultats contenant au plus 2 boules rouges.

Définir $G$ et calculer $\text{card}\;G$

En déduire $\text{card}\;G$

Calculer :

$A_{5}^{3}\;,\quad C_{7}^{4}\;,\quad A_{5}^{4}-C_{8}^{3}+5!\;,\quad\dfrac{10!}{8!}\;,\quad\dfrac{13!}{5!}$

Donner la valeur exacte de chacun des réels suivants :

$C_{5}^{0}+C_{5}^{1}+C_{5}^{2}+C_{5}^{3}+C_{5}^{4}+C_{5}^{5}$

$C_{7}^{0}-C_{7}^{1}+C_{7}^{2}-C_{7}^{3}+C_{7}^{4}-C_{7}^{5}+C_{7}^{6}-C_{7}^{7}$

$C_{6}^{2}+C_{6}^{3}+C_{6}^{4}+C_{6}^{5}\;,\quad C_{8}^{1}+C_{8}^{2}+C_{8}^{3}+C_{8}^{4}+C_{8}^{5}+C_{8}^{6}$

Exprimer les réels suivants sous forme d'un polynôme en $n$ ou d'une fraction rationnelle en $n$ :

$\dfrac{n!}{(n-1)!}\;,\quad\dfrac{n!}{(n-2)!}\;,\quad\dfrac{(n-1)!}{(n-4)!}\;,\quad\dfrac{6C_{n}^{3}}{A_{n}^{5}}$

$C_{n}^{3}-3C_{n}^{2}+2\;,\quad C_{n}^{4}+3A_{n}^{3}-2\dfrac{n!}{(n-3)!}$

Exprimer les réels suivants en fonction de $2^{n}\;,\ n\in\;\mathbb{N}\;:$

$C_{n}^{1}+C_{n}^{2}+C_{n}^{3}+\cdots+C_{n}^{n-1}\;,\quad C_{n}^{2}+C_{n}^{3}+C_{n}^{4}+\cdots+C_{n}^{n-2}$

$C_{n}^{1}-C_{n}^{2}+C_{n}^{3}-C_{n}^{4}+\cdots+(-1)^{n-1}C_{n}^{n-1}$

$C_{n}^{2}-C_{n}^{3}+C_{n}^{4}-C_{n}^{5}+\cdots+(-1)^{n}C_{n}^{n}$

$2!A_{n}^{2}+3!A_{n}^{3}+\cdots+(n-1)!A_{n}^{n-1}$

$2!A_{n}^{2}+3!A_{n}^{3}+4!A_{n}^{4}+\cdots+(n-2)!A_{n}^{n-2}$

$A_{n}^{1}-2!A_{n}^{2}+3!A_{n}^{3}-4!A_{n}^{4}+\cdots+(-1)^{n-1}(n-1)!A_{n}^{n-1}$

Exercice 36

En utilisant les égalités suivantes :

$$1+2+3+\cdots+n=\dfrac{n(n-1)}{2}\text{ et }1^{2}+2^{2}+3^{2}+\cdots+n^{2}=\dfrac{n(n+1)(2n+1)}{6}$$

Montrer que :
$$C_{2}^{2}+C_{3}^{2}+C_{4}^{2}+\cdots+C_{n}^{2}=\dfrac{n(n+1)(2n+1)}{12}-\dfrac{n(n+1)}{4}$$

Développer à l'aide de la formule du binôme de newton :

$(2x+1)^{5}\;,\quad(3x-1)^{4}\;,\quad(-2x+3)^{3}\;,\quad(x^{2}+x+1)^{3}\;,\quad(x^{2}-x+1)^{4}$

Quel est le coefficient de $x^{13}$ dans le développement de :

1) $(x+1)^{20}$

2) $(2x-3)^{17}$

3) $(3x-1)^{5}(2x+1)^{8}$

4) $(x^{2}+x)^{6}$

5) $(-x+2)(-2x+1)^{14}$

soit : $f(x)=(x+1)^{n}\;,\ n\in\;\mathbb{N}$

1) Donner le développement de $(x+1)^{n}$

2) Monter que $f$ est dérivable sur $\mathbb{R}$ et utiliser $f'(x)$ pour montrer que :

$C_{n}^{1}+2C_{n}^{2}+3C_{n}^{3}+\cdots+nC_{n}^{n-1}=n\times 2^{n}\;,\text{ pour tout }n\in\;\mathbb{N}^{\ast}$

Résoudre dans $\mathbb{N}$ les équations suivantes d'inconnue $n$ :

1) $C_{n}^{3}+C_{n}^{2}+C_{n}^{1}-7=0$

2) $(C_{2n+1}^{3})^{2}-4C_{2n+1}^{3}+3=0$

3) $C_{n^{2}}^{n}=C_{n^{2}+n}^{4}$

4) $(C_{4n+1}^{2})^{2}-5C_{4n+1}^{2}+4=0$

5) $C_{n^{2}+n+1}^{n}+3C_{n^{2}+n+1}^{n}+2=0$

6) $(n_{n+2}^{n})^{3}-3(C_{n+2}^{n})^{2}+2=0$

Répondre par oui ou par non justifiant la réponse :

1) En tirant simultanément 3 boules dans une urne contenant 4 boules rouges l'ordre des boules obtenues n'a pas d'importance

2) Lorsqu'on tire simultanément 4 boules dans une urne contenant 4 boules rouges, il y a un seul tirage possible

3) Lorsqu'on tire successivement $p$ boules dans une urne contenant $n$ boules le nombre de tirages possibles est $A_{n}^{p}$

4) Lorsqu'on tire successivement $p$ boules dans une urne contenant $n$ boules, l'ordre des boules obtenues à de l'importance.

5) Lorsqu'on veut élire un comité où les membres ne jouent aucun rôle on ne doit pas tenir de l'ordre des membres de ce comité

6) Lorsqu'on veut élire un comité où il y a un président, un secrétaire et un trésorier, on doit tenir compte de l'ordre des membres de ce comité

7) Lorsqu'on veut élire un comité de 3 membres ne jouant aucun rôle, dans une population de 10 personnes, alors le nombre de comités possibles est $C_{10}^{3}$

8) Lorsqu'on veut élire en comité de 3 membres dont un président, un secrétaire est un trésorier, dans une population de 15 personnes, le nombre total de comités est $A_{15}^{3}$

9) On considère l'ensemble $\Omega=\{a\;,\ b\;,\ c\;,\ d\;,\ e\}$

a) $\{a\;,\ b\;,\ c\}$ est une combinaison d'ordre 3 de $\Omega$

b) $(a\;,\ b\;,\ c)$ est un arrangement d'ordre 3, des 5 éléments de $\Omega$

c) $(a\;,\ a\;,\ b\;,\ c)$ est un arrangement d'ordre 4, des 5 éléments de $\Omega$

d) $(a\;,\ b\;,\ c\;,\ d\;,\ e)$ est une permutation des 5 éléments de $\Omega$

e) le nombre de permutation des 5 éléments de $\Omega$ est $A_{5}^{5}$

f) le nombre de permutations des 5 éléments de $\Omega$ est $5!$

g) le nombre de combinaisons d'ordre 4 de $\Omega$ est $\dfrac{A_{4}^{5}}{4!}$

h) le nombre de combinaisons d'ordre 3 de $\Omega$, contenant l'élément $a$, est $3\times A_{4}^{2}$

i) le nombre d'arrangements d'ordre 3, contenant $a$, des 5 éléments de $\Omega$, est $3C_{4}^{2}$

j) le nombre de 3-listes d'éléments de $\Omega$, contenant $a$, est $3\times 2^{2}$

1) Montrer que le nombre de diagonales d'un polygone convexe de $n$ cotés est $C_{n}^{2}-n\;,\text{ pour }n\geq 3$

2) Exprimer $C_{n}^{2}-n$ sous forme d'une fraction

3) Quel est le nombre de diagonales d'un octogone régulier ?

on considère un polynôme convexe de $n$ cotés, dont les diagonales se coupent deux à deux

1) Montrer le nombre de points d'intersection situés à l'intérieur de ce polygone, des diagonales de ce polygone, est $C_{n}^{4}$

2) En déduire le nombre de points d'intersection de ces diagonales, situés à l'extérieur de ce polynôme

Répondre par oui ou non en justifiant la réponse :

1) Lorsqu'on lance une fois un dé cubique dont les faces sont numérotées de 1 à 6, le nombre d'issues est 6

2) Lorsqu'on lance 2 fois de suite un dé cubique dont les faces sont numérotées de 1 à 6, il y a 36 issues possibles

3) Lorsqu'on lance deux fois une pièce de monnaie, chaque lancer pouvant donner les issues pile $(P)$ ou face $(F)$, l'ensemble des résultats possibles est $\{(P\;,\ P)\;;\ (P\;,\ F)\;;\ (F\;,P)\}$

4) Lorsqu'on lance 2 fois de suite un dé cubique dont les faces sont numérotées de 1 à 6, il y a 7 issues dont la somme est 7

5) Lorsqu'on lance simultanément 3 dés cubiques dont les faces de chacun sont numérotées de 1 à 6, alors il y a $6^{3}$ issues possibles.

6) On dispose d'un dé cubique dont les faces sont numérotées de 1 à 6 de deux urnes $U_{1}\text{ et }U_{2}\;;\ U_{1}$ contient 2 boules rouges et 3 boules noires et $U_{2}$ contient 3 boules noires et deux boules rouges.

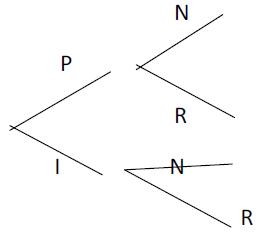
On lance une fois ce dé ; si on obtient un chiffre pair $(P)$, on tire une boule de $U_{1}$ et on peut obtenir

une boule noire $(N)$ ou une boule rouge $(R)$ ; le lancer de ce dé donne un chiffre impair $(I)$, on tire une

boule de l'urne $U_{2}$ et on peut obtenir une rouge $(R)$ ou une boule noire $(N)$

On peut traduire l'énoncé par l'arbre suivant (oui ou non)

7) Une urne contient 3 boules noires et 2 boules rouges.

On effectue deux tirages successifs sans remise dans cette urne

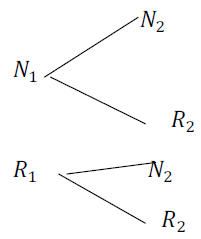
Le premier tirage peut donner une boule noire $(N_{1})$ ou une boule rouge $(R_{1})$, le $2^{eme}$ tirage peut donner une boule noire $N_{2}$ ou une boule rouge $R_{2}$

On peut traduire l'énoncé (oui ou non) par l'arbre suivant

8) les anagrammes du mot $ARA$ sont :

$AAR\;,\ RRA\;,\ RAA\text{ et }ARA$

9) le mot $ARAL$ admet $4!$ Anagrammes

10) $AABA\text{ et }AAAB$ sont des anagrammes de deux mots différents

11) Lorsqu'on tire simultanément $p$ éléments d'un ensemble $\Omega$ contenant $n$ éléments chaque résultat est une combinaison d'ordre $p\text{ de }\Omega$

12) Lorsqu'on tire successivement avec remise 3 éléments d'une urne contenant des cartons 4 numérotés $1\;,\ 2\;,\ 3\text{ et }4\;,$

on peut obtenir les résultats suivants :

$(1\;,\ 1\;,\ 1\;,\ 1)\;,\ (1\;,\ 3\;,\ 2\;,\ 4)\;,\ (1\;,\ 1\;,\ 2\;,\ 2)$

une urne contient 5 boules : 3 rouges et 2 noires

On tire simultanément 2 boules de cette urne et on note $\Omega$

L'ensemble des résultats possibles :

Déterminer :

1) $\text{Card}\;\Omega$

2) Le nombre de résultats contenant deux boules de même couleur

3) Le nombre de résultats contenant deux boules de couleurs différentes

On tire simultanément 3 boules d'une urne contenant 3 boules rouges 4 boules blanches et 4 boules noires

1) Déterminer le nombre de résultats possibles

2) On note :

$A$ l'ensemble des résultats unicolores,

$B$ l'ensemble des résultats tricolores,

$C$ l'ensemble des résultats contenant 2 boules rouges et une boule noire,

$D$ l'ensemble des résultats contenant 2 boules rouges et une boule d'une autre couleur

$E$ l'ensemble des résultats contenant 2 boules d'une même couleur et une boule d'une autre couleur

Calculer
$$\text{Card}\;A\;,\text{ Card}\;B\;,\text{ Card}\;C\;,\text{ Card}\;D\text{ et }\text{Card}\;E$$

3) Soit $F$ l'ensemble des résultats contenant au moins une boule noire

a) Définir $\overline{F}$ et calculer $\text{Card}\;\overline{F}$

b) En déduire $\text{Card}\;F$

4) Soit $G$ l'ensemble des résultats contenant au plus 2 boules rouges

a) Définir $\overline{G}$ et calculer $\text{Card}\;\overline{G}$

b) En déduire $\text{Card}\;G$

Exercice 47

on tire successivement sans remise 4 boules d'une urne contenant 3 boules, 3 boules blanches et 4 boules noires

1) Déterminer le nombre de résultats possibles

2) Déterminer le nombre de résultats contenant :

a) Exactement 2 boules rouges

b) Exactement 2 boules noires et une boule blanche

c) Au plus de 3 boules noires

d) Au moins une boule blanche

on tire successivement avec remise 3 boules d'une urne contenant 3 boules, 2 boules noires et 2 boules blanches

1) Quel est le nombre de résultats possibles ?

2) Déterminer le nombre de résultats unicolores

3) Déterminer le nombre de résultats tricolores

4) Déterminer le nombre de résultats ne contenant aucune boule noire

5) Déterminer :

a) le nombre de résultats contenant au moins une boule noir

b) le nombre de résultats contenant au plus 2 boules rouges

20 personnes dont 10 femmes et 10 hommes veulent élire un comité de 3 personnes pour les représenter à une réunion

1) Quel est le nombre de comités possibles

2) Déterminer le nombre de comités ne contenant aucun homme

3) Quel est le nombre de comités contenant exactement un homme ?

4) Quel est le nombre de comités contenant au plus 2 hommes ?

5) Quel est le nombre de comités contenant au moins une femme ?

6) Quel est le nombre de comités contenant monsieur $X$, personne figurant parmi les 20 personnes

7) Quel est nombre de comités contenant Madame $Y$, personne figurant parmi les 20 personnes

8) Si monsieur $X$ et madame $Y$ ne peut pas être dans un même comité, quel est le nombre de comités possibles ?

15 personnes dont 5 femmes doivent élire un bureau formé d'un président $(P)$, d'un secrétaire $(S)$ et d'un trésorier $(T)$, sans cumul de poste.

1) Quel est le nombre de bureau possibles ?

2) Déterminer le nombre de bureaux contenant :

a) Exactement un homme

b) Exactement deux femmes

c) Au plus 2 hommes

d) Au moins une femme

3) Si Monsieur $X$ et Madame $Y$ doivent être dans le bureau quel est le nombre de bureaux possible ?

une urne contient 2 boules rouges $R_{1}\text{ et }R_{2}$, 3 boules blanches $B_{1}\;,\ B_{2}\text{ et }B_{3}$, 2 boules noires $N_{1}\text{ et }N_{2}$

On tire successivement avec remise 4 boules de cette urne

1) Quel est le nombre de tirages donnant exactement 2 boules rouges et une boule numérotée 1

2) Donner le nombre tirage donnant exactement une boule noire et boules numérotées 2

on tire simultanément 5 cartes d'un jeu de 32 cartes, pour obtenir une main de 5 cartes

1) Calculer le nombre de mains possibles

2) Déterminer le nombre de mains contenant :

a) exactement deux rois

b) exactement deux dames et 3 As

c) 5 piques

d) exactement 3 trèfles

e) au moins un carreau

f) au plus 4 cœurs

g) exactement un Valet et 2 piques

Quel est le nombre de résultats $(a\;,\ b\;,\ c)$ tels que :

1) L'équation $ax^{2}+bx+c=0$ ait deux solutions distinctes

2) L'équation $ax^{2}+bx+c=0$ ait une solution double

3) L'équation $ax^{2}+bx+c=0$ ait impossible dans $\mathbb{R}$

4) $a+b+c=8$

On lance simultanément 3 dés identiques dont les faces de chacun sont numérotées de 1 à 6 et on appelle résultat l'ensemble $\{a\;,\ b\;,\ c\}$ des 3 numéros obtenus

1) Quel est le nombre de résultats possibles ?

2) Quel est le nombre de résultats tels que $a+b+c=4$ ?

On considère $n$ droites $(D_{1})\;,\ (D_{2})\;,\ (D_{3})$ telles que trois quelconques d'entre elles ne soient pas concourantes, avec $n\in\;\mathbb{N}^{\ast}$

On note par $U_{n}$ le nombre de régions délimités par ces $n$ droites dans le plan

Exemple :

Si $n=1$, on a une seule droite $(D_{1})$ qui découpe 2 région $R_{1}\text{ et }R_{2}$ sans le plan

Donc $U_{1}=2$

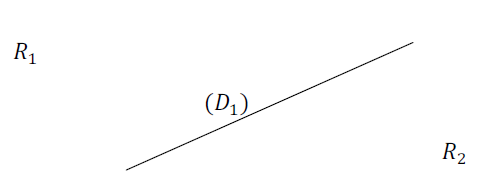
Si $n=2$, on a deux droites qui délimitent 4 régions $R_{1}\;,\ R_{2}\;,R_{3}\text{ et }R_{4}$

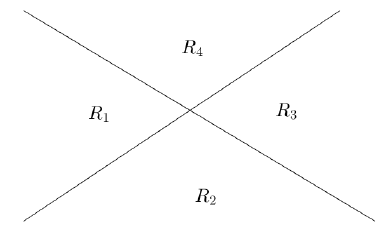
Si $n=3$, on a 3 droites $(D_{1})\;,\ (D_{2})\;,\ (D_{3})$

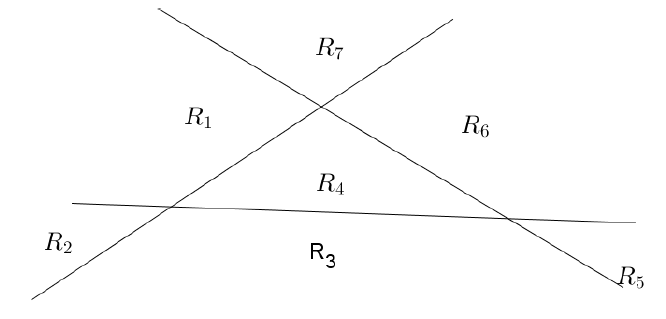
1) Montrer que :
$$\forall n\in\;\mathbb{N}^{\ast}\;,\ U_{n+1}=U_{n}+n+1$$

2) En déduire que :
$$\forall n\in\mathbb{N}^{\ast}\;,\ U_{n}=\dfrac{n^{2}+n+2}{2}$$