Vous êtes ici

Solution des exercices : Angles - Trigonométrie - 2nd

Classe:

Seconde

Exercice 1

1) Déterminons la mesure principale de :

$\dfrac{27\pi}{3}\;,\ \dfrac{77\pi}{4}\;,\ -\dfrac{81\pi}{5}$

$\centerdot\$ mesure principale de

$\dfrac{27\pi}{3}$

Soit

$\alpha$ la mesure principale de

$\dfrac{27\pi}{3}$ alors,

$-\pi<\alpha\leq\pi$ et on a :

$\dfrac{27\pi}{3}=\alpha+2k\pi\quad\text{avec, }k\in\mathbb{Z}$

Donc,

$\alpha=\dfrac{27\pi}{3}-2k\pi$

Déterminons alors l'entier relatif

$k.$

On a :

$\begin{array}{rcl} -\pi<\alpha\leq\pi&\Leftrightarrow&-\pi<\dfrac{27\pi}{3}-2k\pi \leq\pi\\ \\&\Leftrightarrow&-\pi-\dfrac{27\pi}{3}<-2k\pi\leq\pi-\dfrac{27\pi}{3}\\ \\&\Leftrightarrow&\dfrac{27\pi}{3}-\pi\leq 2k\pi<\dfrac{27\pi}{3}+\pi\\ \\&\Leftrightarrow&\dfrac{24\pi}{3}\leq 2k\pi<\dfrac{30\pi}{3}\\ \\&\Leftrightarrow&8\leq 2k<10\\ \\&\Leftrightarrow&4\leq k<5\end{array}$

Par suite :

$k=4$

Ainsi, en remplaçant

$k$ par sa valeur, dans l'expression de

$\alpha$ , on trouve :

$\boxed{\alpha=\pi}$

$\centerdot\$ mesure principale de

$\dfrac{77\pi}{4}$

Soit

$\beta$ la mesure principale de

$\dfrac{77\pi}{4}$ alors,

$-\pi<\beta\leq\pi$ et on a :

$\dfrac{77\pi}{4}=\beta+2k\pi\quad\text{avec, }k\in\mathbb{Z}$

Ainsi,

$\beta=\dfrac{77\pi}{4}-2k\pi$

Détermination de l'entier relatif

$k.$

On a :

$\begin{array}{rcl} -\pi<\beta\leq\pi&\Leftrightarrow&-\pi<\dfrac{77\pi}{4}-2k\pi \leq\pi\\ \\&\Leftrightarrow&-\pi-\dfrac{77\pi}{4}<-2k\pi\leq\pi-\dfrac{77\pi}{4}\\ \\&\Leftrightarrow&\dfrac{77\pi}{4}-\pi\leq 2k\pi<\dfrac{77\pi}{4}+\pi\\ \\&\Leftrightarrow&\dfrac{73\pi}{4}\leq 2k\pi<\dfrac{81\pi}{4}\\ \\&\Leftrightarrow&18.25\leq 2k<20.25\\ \\&\Leftrightarrow&9.125\leq k<10.125\end{array}$

On obtient :

$k=10$

Ce qui donne alors :

$\boxed{\beta=-\dfrac{3\pi}{4}}$

$\centerdot\$ mesure principale de

$-\dfrac{81\pi}{5}$

Soit

$\gamma$ la mesure principale de

$-\dfrac{81\pi}{5}$ alors,

$-\pi<\gamma\leq\pi$ et on a :

$-\dfrac{81\pi}{5}=\gamma+2k\pi\quad\text{avec, }k\in\mathbb{Z}$

Ce qui entraine :

$\gamma=-\dfrac{81\pi}{5}-2k\pi$

Déterminons l'entier relatif

$k.$

On a :

$\begin{array}{rcl} -\pi<\gamma\leq\pi&\Leftrightarrow&-\pi<-\dfrac{81\pi}{5}-2k\pi \leq\pi\\ \\&\Leftrightarrow&-\pi+\dfrac{81\pi}{5}<-2k\pi\leq\pi+\dfrac{81\pi}{5}\\ \\&\Leftrightarrow&-\dfrac{81\pi}{5}-\pi\leq 2k\pi<-\dfrac{81\pi}{5}+\pi\\ \\&\Leftrightarrow&-\dfrac{86\pi}{5}\leq 2k\pi<-\dfrac{76\pi}{5}\\ \\&\Leftrightarrow&-17.2\leq 2k<-15.2\\ \\&\Leftrightarrow&-8.6\leq k<-7.6\end{array}$

On obtient alors :

$k=-8$

Par suite :

$\boxed{\gamma=-\dfrac{\pi}{5}}$

2) Donnons les valeurs exactes de :

$\cos\dfrac{2\pi}{3}\;,\ \sin\dfrac{2\pi}{3}\;,\ \cos\dfrac{25\pi}{4}\;,\ \sin\dfrac{25\pi}{4}\;,\ \sin\dfrac{7\pi}{4}\;,\ \sin\dfrac{213\pi}{6}\;,\ \cos\dfrac{-77\pi}{3}$

$\centerdot\ \$ valeur exacte de

$\cos\dfrac{2\pi}{3}$

Comme

$\dfrac{2\pi}{3}=\pi-\dfrac{\pi}{3}$ alors, on a :

$\begin{array}{rcl} \cos\dfrac{2\pi}{3} &=&\cos\left(\pi-\dfrac{\pi}{3}\right)\\ \\&=&-\cos\dfrac{\pi}{3}\\ \\&=&-\dfrac{1}{2}\end{array}$

D'où,

$\boxed{\cos\dfrac{2\pi}{3}=-\dfrac{1}{2}}$

$\centerdot\ \$ valeur exacte de

$\sin\dfrac{2\pi}{3}$

En utilisant les propriétés trigonométriques du sinus, on obtient :

$\begin{array}{rcl}\sin\dfrac{2\pi}{3} &=&\sin\left(\pi-\dfrac{\pi}{3}\right)\\ \\&=&\sin\dfrac{\pi}{3}\\ \\&=& \dfrac{\sqrt{3}}{2}\end{array}$

Donc,

$\boxed{\sin\dfrac{2\pi}{3}=\dfrac{\sqrt{3}}{2}}$

$\centerdot\ \$ valeur exacte de

$\cos\dfrac{25\pi}{4}$

On sait que :

$\dfrac{25\pi}{4}=\dfrac{\pi}{4}+6\pi.$

Donc, d'après les propriétés trigonométriques du cosinus, on a :

$\begin{array}{rcl} \cos\dfrac{25\pi}{4} &=&\cos\left(\dfrac{\pi}{4}+6\pi\right)\\ \\&=&\cos\dfrac{\pi}{4}\\ \\&=& \dfrac{\sqrt{2}}{2}\end{array}$

D'où,

$\boxed{\cos\dfrac{25\pi}{4}=\dfrac{\sqrt{2}}{2}}$

$\centerdot\ \$ valeur exacte de

$\sin\dfrac{25\pi}{4}$

En utilisant les propriétés trigonométriques du sinus, on trouve :

$\begin{array}{rcl} \sin\dfrac{25\pi}{4}&=&\sin\left(\dfrac{\pi}{4}+6\pi\right)\\ \\&=&\sin\dfrac{\pi}{4}\\ \\&=&\dfrac{\sqrt{2}}{2}\end{array}$

Soit :

$\boxed{\sin\dfrac{25\pi}{4}=\dfrac{\sqrt{2}}{2}}$

$\centerdot\ \$ valeur exacte de

$\sin\dfrac{7\pi}{4}$

Comme

$\dfrac{7\pi}{4}=2\pi-\dfrac{\pi}{4}$ alors, on obtient :

$\begin{array}{rcl} \sin\dfrac{7\pi}{4}&=&\sin\left(2\pi-\dfrac{\pi}{4}\right)\\\\&=&\sin\left(-\dfrac{\pi}{4}\right)\\ \\&=&-\sin\dfrac{\pi}{4}\\ \\&=&-\dfrac{\sqrt{2}}{2}\end{array}$

D'où :

$\boxed{\sin\dfrac{7\pi}{4}=-\dfrac{\sqrt{2}}{2}}$

$\centerdot\ \$ valeur exacte de

$\sin\dfrac{213\pi}{6}$

On a :

$\dfrac{213\pi}{6}=36\pi-\dfrac{3\pi}{6}=36\pi-\dfrac{\pi}{2}$

Donc, en utilisant les propriétés trigonométriques du sinus, on trouve :

$\begin{array}{rcl} \sin\dfrac{213\pi}{6}&=&\sin\left(36\pi-\dfrac{\pi}{2}\right)\\\\&=&\sin\left(-\dfrac{\pi}{2}\right)\\ \\&=&-\sin\dfrac{\pi}{2}\\\\&=&-1\end{array}$

Par suite,

$\boxed{\sin\dfrac{213\pi}{6}=-1}$

$\centerdot\ \$ valeur exacte de

$\cos\dfrac{-77\pi}{3}$

On a :

$\dfrac{-77\pi}{3}=\dfrac{\pi}{3}-26\pi$

Donc,

$\begin{array}{rcl} \cos\dfrac{-77\pi}{3}&=&\cos\left(\dfrac{\pi}{3}-26\pi\right)\\\\&=&\cos\dfrac{\pi}{3}\\ \\&=&\dfrac{1}{2}\end{array}$

Ainsi,

$\boxed{\cos\dfrac{-77\pi}{3}=\dfrac{1}{2}}$

$\tan\left(\dfrac{7\pi}{6}\right)\;,\ \tan\left(\dfrac{3\pi}{4}\right)\;,\ \tan\left(\dfrac{-5\pi}{6}\right)$

$\centerdot\ \$ valeur exacte de

$\tan\left(\dfrac{7\pi}{6}\right)$

On sait que :

$\dfrac{7\pi}{6}=\pi+\dfrac{\pi}{6}$ donc,

$\begin{array}{rcl}\tan\left(\dfrac{7\pi}{6}\right)&=&\tan\left(\pi+\dfrac{\pi}{6}\right)\\\\&=&\tan\left(\dfrac{\pi}{6}\right)\\\\&=&\dfrac{\sqrt{3}}{3}\end{array}$

D'où,

$\boxed{\tan\left(\dfrac{7\pi}{6}\right)=\dfrac{\sqrt{3}}{3}}$

$\centerdot\ \$ valeur exacte de

$\tan\left(\dfrac{3\pi}{4}\right)$

Soit :

$\dfrac{3\pi}{4}=\pi-\dfrac{\pi}{4}$

Alors,

$\begin{array}{rcl}\tan\left(\dfrac{3\pi}{4}\right)&=&\tan\left(\pi-\dfrac{\pi}{4}\right)\\\\&=&-\tan\left(\dfrac{\pi}{4}\right)\\\\&=&-1\end{array}$

Ainsi,

$\boxed{\tan\left(\dfrac{3\pi}{4}\right)=-1}$

$\centerdot\ \$ valeur exacte de

$\tan\left(\dfrac{-5\pi}{6}\right)$

On a :

$\dfrac{-5\pi}{6}=\dfrac{7\pi}{6}-2\pi$

Donc,

$\begin{array}{rcl}\tan\left(\dfrac{-5\pi}{6}\right)&=&\tan\left(\dfrac{7\pi}{6}-2\pi\right)\\\\&=&\tan\left(\dfrac{7\pi}{6}\right)\end{array}$

Or, d'après ce qui précède,

$\tan\left(\dfrac{7\pi}{6}\right)=\dfrac{\sqrt{3}}{3}$

Par suite,

$\boxed{\tan\left(\dfrac{-5\pi}{6}\right)=\dfrac{\sqrt{3}}{3}}$

Exercice 2

Transformons les expression suivantes :

$\begin{array}{rcl} A&=&3\cos(-x)+2\sin\left(\dfrac{\pi}{2}-x\right)+4\sin x+\cos x\\\\&=&3\cos x+2\cos x+4\sin x+\cos x\\\\&=&6\cos x+4\sin x\end{array}$

Donc,

$\boxed{A=6\cos x+4\sin x}$

$\begin{array}{rcl} B&=&2\sin\left(\dfrac{\pi}{2}+x\right)+5\cos(\pi-x)-3\sin(-x)-\cos x\\\\&=&2\cos x-5\cos x+3\sin x-\cos x\\\\&=&-4\cos x+3\sin x\end{array}$

D'où,

$\boxed{B=-4\cos x+3\sin x}$

$\begin{array}{rcl} C&=&-\sin(\pi-x)+\cos\left(\dfrac{\pi}{2}+x\right)-\sin(\pi-x)\\\\&=&-\sin x-\sin x-\sin x\\\\&=&-3\sin x\end{array}$

Ainsi,

$\boxed{C=-3\sin x}$

$\begin{array}{rcl} D&=&\sin\left(\dfrac{\pi}{2}+x\right)+\cos(x-\pi)+\sin\left(x+\dfrac{3\pi}{2}\right)+\cos(x+\pi)\\\\&=&\cos x+\cos(-(\pi-x))+\sin\left(\pi+\left(\dfrac{\pi}{2}+x\right)\right)-\cos x\\\\&=&\cos x+\cos(\pi-x)-\sin\left(\dfrac{\pi}{2}+x\right)-\cos x\\\\&=&\cos x-\cos x-\cos x-\cos x\\\\&=&-2\cos x\end{array}$

Donc,

$\boxed{D=-2\cos x}$

$\begin{array}{rcl} E&=&2\cos\left(\dfrac{3\pi}{2}-\pi+x\right)-2\sin(x-2\pi)+5\sin\left(\dfrac{5\pi}{2}+x\right)\\\\&=&2\cos\left(\dfrac{\pi}{2}+x\right)-2\sin x+5\sin\left(2\pi+\left(\dfrac{\pi}{2}+x\right)\right)\\\\&=&-2\sin x-2\sin x+5\sin\left(\dfrac{\pi}{2}+x\right)\\\\&=&-2\sin x-2\sin x+5\cos x\\\\&=&-4\sin x+5\cos x\end{array}$

Par suite,

$\boxed{E=-4\sin x+5\cos x}$

Exercice 3

Établissons les égalités suivantes :

$\cos^{2}x-\sin^{2}x=2\cos^{2}x-1=1-2\sin^{2}x$

Soit la relation suivante :

$\cos^{2}x-\sin^{2}x\qquad(*)$

Alors, on sait que :

$\cos^{2}x+\sin^{2}x=1$

Ce qui entraine :

$\cos^{2}x=1-\sin^{2}x\ \text{ et }\ \sin^{2}x=1-\cos^{2}x$

Ainsi, en remplaçant

$\sin^{2}x$ par son expression, dans la relation

$(*)$ , on obtient :

$\begin{array}{rcl}\cos^{2}x-\sin^{2}x&=&\cos^{2}x-\left(1-\cos^{2}x\right)\\\\&=&\cos^{2}x-1+\cos^{2}x\\\\&=&2\cos^{2}x-1\end{array}$

D'où,

$\boxed{\cos^{2}x-\sin^{2}x=2\cos^{2}x-1}$

De la même manière, dans la relation

$(*)$ , en remplaçant

$\cos^{2}x$ par son expression, on trouve :

$\begin{array}{rcl}\cos^{2}x-\sin^{2}x&=&1-\sin^{2}x-\sin^{2}x\\\\&=&1-2\sin^{2}x\end{array}$

Ainsi,

$\boxed{\cos^{2}x-\sin^{2}x=1-2\sin^{2}x}$

$\cos^{4}x+\sin^{4}x=1-2\cos^{2}x\sin^{2}x$

Comme

$\cos^{2}x+\sin^{2}x=1$ alors, en élevant au carré, on obtient :

$\begin{array}{rcl}\cos^{2}x+\sin^{2}x=1^{2}&\Rightarrow&\left(\cos^{2}x+\sin^{2}x\right)^{2}=1\\\\&\Rightarrow&\cos^{4}x+2\cos^{2}x\sin^{2}x+\sin^{4}x=1\\\\&\Rightarrow&\cos^{4}x+\sin^{4}x=1-2\cos^{2}x\sin^{2}x\end{array}$

Par suite,

$\boxed{\cos^{4}x+\sin^{4}x=1-2\cos^{2}x\sin^{2}x}$

$\left(\cos x+\sin x\right)^{2}+\left(\cos x-\sin x\right)^{2}=2$

En utilisant la forme développée des identités remarquables, on obtient :

$\begin{array}{rcl}\left(\cos x+\sin x\right)^{2}+\left(\cos x-\sin x\right)^{2}&=&\left(\cos^{2}x+2\cos x\sin x+\sin^{2}x\right)+\left(\cos^{2}x-2\cos x\sin x+\sin^{2}x\right)\\\\&=&\cos^{2}x+\cos^{2}x+\sin^{2}x+\sin^{2}x+2\cos x\sin x-2\cos x\sin x\\\\&=&2\cos^{2}x+2\sin^{2}x\\\\&=&2\left(\underbrace{\cos^{2}x+\sin^{2}x}_{=1}\right)\\\\&=&2\end{array}$

D'où,

$\boxed{\left(\cos x+\sin x\right)^{2}+\left(\cos x-\sin x\right)^{2}=2}$

Exercice 4

Donnons la longueur d'un demi-cercle de rayon

$2\;cm$ , et d'un quart de cercle de rayon

$4\;cm.$

Un demi-cercle engendre un secteur angulaire de mesure :

$\alpha=\pi$

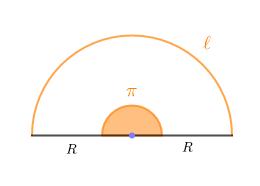
Donc, la longueur

$\ell$ de l'arc que représente ce demi-cercle est donnée par :

$\ell=R\times\alpha\quad\text{ avec }R\text{ rayon du cercle}$

Par suite,

$\begin{array}{rcl}\ell&=&R\times\alpha\\\\&=&2\times\pi\\\\&=&6.28\end{array}$

Ainsi,

$\boxed{\ell=6.28\;cm}$

De la même manière, un quart de cercle engendre un secteur angulaire de mesure :

$\alpha=\dfrac{\pi}{2}$

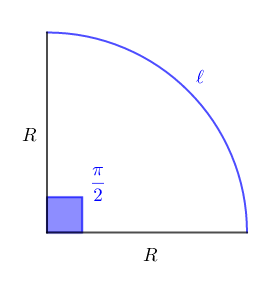
Alors, la longueur

$\ell$ de l'arc représenté par ce quart de cercle est donnée par :

$\ell=R\times\alpha\quad\text{ avec }R\text{ rayon du cercle}$

Donc,

$\begin{array}{rcl}\ell&=&R\times\alpha\\\\&=&4\times\dfrac{\pi}{2}\\\\&=&2\pi\\\\&=&6.28\end{array}$

D'où,

$\boxed{\ell=6.28\;cm}$

Exercice 5

1) Complétons le tableau suivant, où

$l$ désigne la longueur de l'arc de cercle de rayon

$R$ , intercepté par l'angle

$\alpha$ mesuré en degrés.

Pour cela , nous allons convertir

$\alpha$ en radians.

En effet, on a :

$l=\theta\times R$

avec,

$\theta$ l'angle, en radians, intercepté par l'arc de cercle de longueur

$l.$

Soit

$\alpha$ l'angle en degrés correspondant à

$\theta.$

On a alors :

$\begin{array}{rcl}\pi&\longmapsto&180^{\circ}\\\\\theta&\longmapsto&\alpha\end{array}$

En appliquant les rapports de proportionnalité, on obtient :

$\dfrac{\theta}{\pi}=\dfrac{\alpha}{180}\ \Rightarrow\ \theta=\dfrac{\alpha\times\pi}{180}$

Ainsi, on a :

$\boxed{l=\dfrac{\alpha\times\pi\times R}{180}}$

Par conséquent,

$\boxed{\alpha=\dfrac{l\times 180}{\pi R}}$

D'où, le tableau suivant :

$\begin{array}{|c|c|c|c|c|c|}\hline l&\pi R/3&2\pi R/3&\pi R/4&\pi R/6&2\pi R/5\\ \hline\alpha&60&120&45&30&72\\ \hline\end{array}$

2) Complétons le tableau suivant, où

$l$ désigne la longueur de l'arc de cercle de rayon

$R$ , intercepté par l'angle

$\alpha$ mesuré en radians.

Comme

$\alpha$ est en radians alors, on a :

$\boxed{l=\alpha\times R\ \Rightarrow\ \alpha=\dfrac{l}{R}}$

Appliquons alors ces relations pour compléter le tableau suivant :

$\begin{array}{|c|c|c|c|c|c|}\hline l&2\pi R&R&\pi R/6&2\pi R/3&5\pi R/8 \\ \hline\alpha&2\pi&1&\pi /6&2\pi/3&5\pi /8\\ \hline\end{array}$

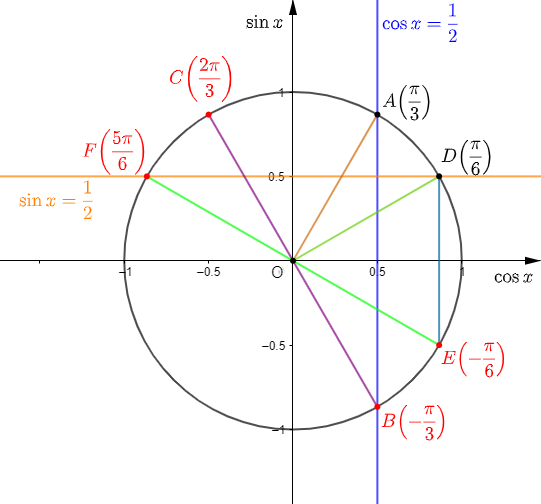
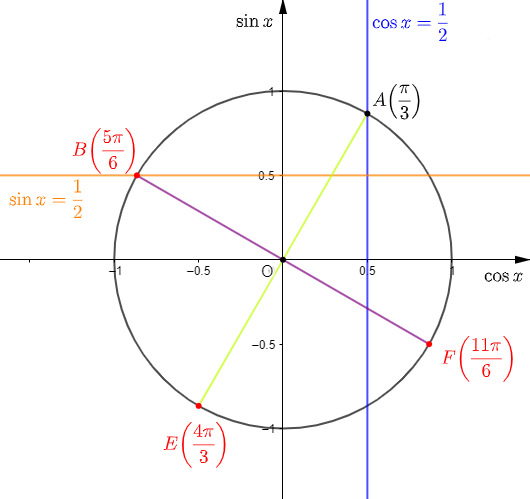
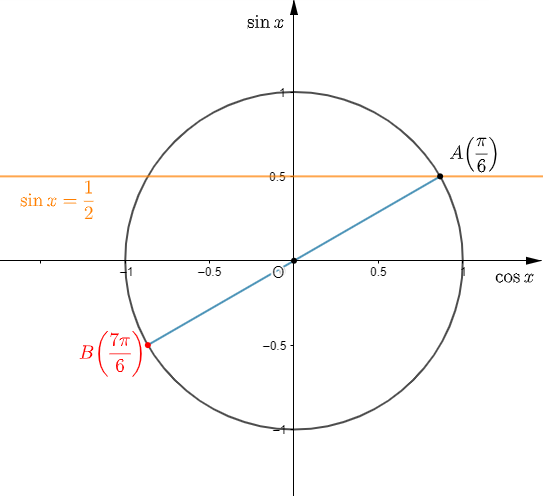
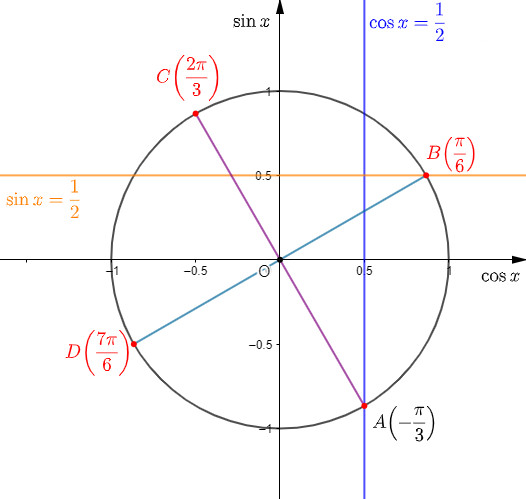
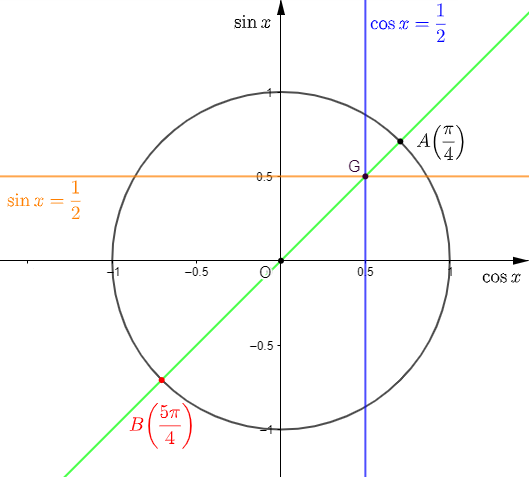
Exercice 6

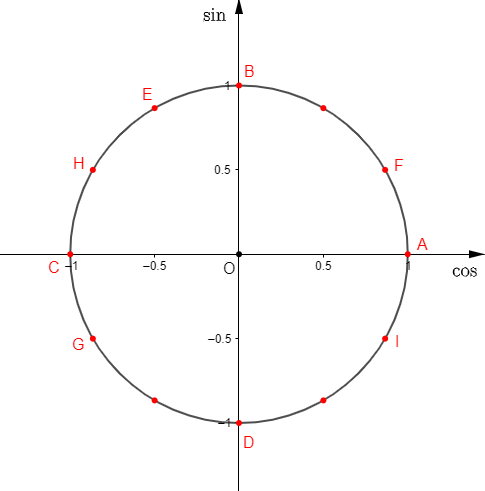
On considère la figure suivante :

1) Les réels

$\dfrac{2\pi}{3}\$ et

$\ -\dfrac{4\pi}{3}$ sont ceux qui représentent une abscisse curviligne du point

$E.$

En effet, on a :

$\dfrac{2\pi}{3}=\pi-\dfrac{\pi}{3}$

Donc, le point d'abscisse curviligne

$\dfrac{2\pi}{3}$ est le symétrique, par rapport à l'axe des ordonnées, du point d'abscisse curviligne

$\dfrac{\pi}{3}.$

Ce qui correspond au point

$E.$

Pour trouver le point d'abscisse curviligne

$\dfrac{\pi}{3}$ , il suffit de tracer la droite parallèle à l'axe des ordonnées et passant par

$x=\dfrac{1}{2}.$

Cette droite coupe le cercle trigonométrique en deux points d'abscisses curvilignes

$\dfrac{\pi}{3}\$ et

$\ -\dfrac{\pi}{3}.$

Par ailleurs, on a :

$-\dfrac{4\pi}{3}=-\dfrac{\pi}{3}-\pi$

Ainsi, le point d'abscisse curviligne

$-\dfrac{4\pi}{3}$ est le symétrique, par rapport à

$O$ , du point d'abscisse curviligne

$-\dfrac{\pi}{3}.$

Cela correspond exactement au point

$E.$

Par conséquent,

$\dfrac{2\pi}{3}\$ et

$\ -\dfrac{4\pi}{3}$ sont les seuls réels de la liste, représentant une abscisse curviligne du point

$E.$

2) Déterminons les points du cercle trigonométrique qui ont pour abscisse curviligne les réels suivants :

$\dfrac{3\pi}{2}\;;\ \pi\;;\ \dfrac{\pi}{6}\;;\ \dfrac{5\pi}{6}\;;\ \dfrac{7\pi}{6}\;;\ \dfrac{11\pi}{6}$

Soit :

$\dfrac{3\pi}{2}=\dfrac{\pi}{2}+\pi$

Cela correspond alors au point

$D.$

Ce qui signifie que

$D$ est le point d'abscisse curviligne

$\dfrac{3\pi}{2}.$

L'abscisse curviligne

$\pi$ est associée au point

$C.$

$\dfrac{\pi}{6}$ correspond au point

$F.$

On a :

$\dfrac{5\pi}{6}=\pi-\dfrac{\pi}{6}$

Alors, le point d'abscisse curviligne

$\dfrac{5\pi}{6}$ est le symétrique, par rapport à l'axe des ordonnées, du point d'abscisse curviligne

$\dfrac{\pi}{6}.$

Ce qui correspond au point

$H.$

Donc,

$H$ est le point d'abscisse curviligne

$\dfrac{5\pi}{6}.$

Par ailleurs, on constate que :

$\dfrac{7\pi}{6}=\dfrac{\pi}{6}+\pi$

Ce qui signifie que le symétrique, par rapport à

$O$ , du point d'abscisse curviligne

$\dfrac{\pi}{6}$ , sera associé à l'abscisse curviligne

$\dfrac{7\pi}{6}.$

D'après la figure ci-dessous, cela correspond au pont

$G.$

D'où,

$G$ est le point d'abscisse curviligne

$\dfrac{7\pi}{6}.$

Enfin, on a :

$\dfrac{11\pi}{6}=-\dfrac{\pi}{6}+2\pi$

Donc, le point d'abscisse curviligne

$-\dfrac{\pi}{6}$ est confondu au point d'abscisse curviligne

$\dfrac{11\pi}{6}.$

Or, le point

$I$ symétrique, par rapport à l'axe des abscisses, du point

$F$ d'abscisse curviligne

$\dfrac{\pi}{6}$ , est associé à l'abscisse curviligne

$-\dfrac{\pi}{6}.$

Par conséquent,

$I$ est aussi le point d'abscisse curviligne

$\dfrac{11\pi}{6}.$

Exercice 7

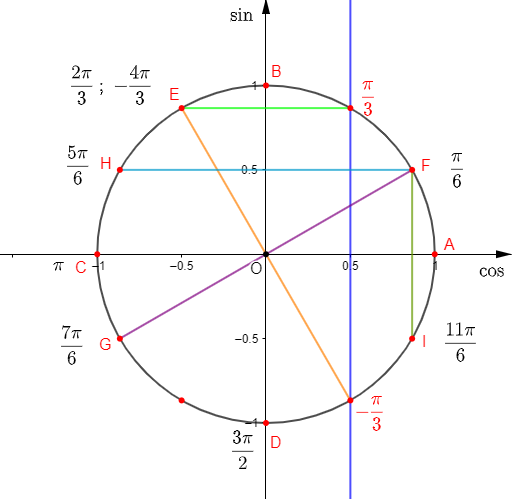
Donnons un moyen géométrique de placer sur le cercle trigonométrique les points d'abscisses curvilignes :

$\dfrac{\pi}{3}\;;\ -\dfrac{\pi}{3}\;;\ \dfrac{2\pi}{3}\;;\ \dfrac{\pi}{6}\;;\ -\dfrac{\pi}{6}\;;\ \dfrac{5\pi}{6}$

En effet, on a :

$\cos\left(\dfrac{\pi}{3}\right)=\cos\left(-\dfrac{\pi}{3}\right)=\dfrac{1}{2}$

Donc, traçons la droite parallèle à l'axe des ordonnées et passant par

$\dfrac{1}{2}.$

Alors, cette droite coupe le cercle trigonométrique aux points

$A\$ et

$\ B$ d'abscisses curvilignes respectives

$\dfrac{\pi}{3}\$ et

$\ -\dfrac{\pi}{3}.$

Aussi, on sait que :

$\dfrac{2\pi}{3}=-\dfrac{\pi}{3}+\pi$

Ce qui signifie que le point

$C$ d'abscisse curviligne

$\dfrac{2\pi}{3}$ est le symétrique, par rapport à

$O$ , du point

$B$ d'abscisse curviligne

$-\dfrac{\pi}{3}.$

Par ailleurs, on a :

$\sin\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2}$

Donc, la droite passant par

$\dfrac{1}{2}$ et parallèle à l'axe des abscisses coupe le cercle trigonométrique au points

$D$ d'abscisse curviligne

$\dfrac{\pi}{6}.$

Par suite,

$E$ d'abscisse curviligne

$-\dfrac{\pi}{6}$ est le symétrique, par rapport à l'axe des abscisses, du point

$D.$

Enfin, on a :

$\dfrac{5\pi}{6}=-\dfrac{\pi}{6}+\pi$

Alors, cela signifie que le point

$F$ , d'abscisse curviligne

$\dfrac{5\pi}{6}$ , est le symétrique, par rapport à

$O$ , du point

$E$ d'abscisse curviligne

$-\dfrac{\pi}{6}.$

Exercice 8

Plaçons sur le cercle trigonométrique les points d'abscisses curvilignes :

$\dfrac{\pi}{3}+\dfrac{k\pi}{2}\;,\ k$ entier relatif

Choisissons le sens positif puis, remplaçons

$k$ successivement, par

$0\;;\ 1\;;\ 2\;;\ \ldots\;;\$ jusqu'à une valeur égale à

$\dfrac{\pi}{3}+2\pi.$

On obtient alors les points suivants d'abscisses curvilignes :

$\dfrac{\pi}{3}+\dfrac{0\pi}{2}=\dfrac{\pi}{3}$

$\dfrac{\pi}{3}+\dfrac{\pi}{2}=\dfrac{5\pi}{6}$

$\dfrac{\pi}{3}+\dfrac{2\pi}{2}=\dfrac{4\pi}{3}$

$\dfrac{\pi}{3}+\dfrac{3\pi}{2}=\dfrac{11\pi}{6}$

$\dfrac{\pi}{3}+\dfrac{4\pi}{2}=\dfrac{\pi}{3}+2\pi$

Ainsi, nous allons placer les points

$A\;,\ B\;,\ E\$ et

$\ F$ d'abscisses curvilignes respectives :

$\dfrac{\pi}{3}\;;\ \dfrac{5\pi}{6}\;;\ \dfrac{4\pi}{3}\;;\ \dfrac{11\pi}{6}$

$\dfrac{\pi}{6}+k\pi\;,\ k$ entier relatif

En choisissant le sens positif puis, en remplaçant

$k$ successivement, par

$0\;;\ 1\;;\ \ldots\;;\$ jusqu'à une valeur égale à

$\dfrac{\pi}{6}+2\pi$ , on obtient :

$\dfrac{\pi}{6}+0\pi=\dfrac{\pi}{6}$

$\dfrac{\pi}{6}+\pi=\dfrac{7\pi}{6}$

$\dfrac{\pi}{6}+2\pi=\dfrac{\pi}{6}+2\pi$

Donc, nous allons placer les points

$A\$ et

$\ B$ d'abscisses curvilignes respectives :

$\dfrac{\pi}{6}\;;\ \dfrac{7\pi}{6}$

$-\dfrac{\pi}{3}+\dfrac{k\pi}{2}\;,\ k$ entier relatif

De la même manière, en remplaçant

$k$ successivement, par

$0\;;\ 1\;;\ 2\;;\ \ldots\;;\$ jusqu'à une valeur égale à

$-\dfrac{\pi}{3}+2\pi$ , on trouve :

$-\dfrac{\pi}{3}+\dfrac{0\pi}{2}=-\dfrac{\pi}{3}$

$-\dfrac{\pi}{3}+\dfrac{\pi}{2}=\dfrac{\pi}{6}$

$-\dfrac{\pi}{3}+\dfrac{2\pi}{2}=\dfrac{2\pi}{3}$

$-\dfrac{\pi}{3}+\dfrac{3\pi}{2}=\dfrac{7\pi}{6}$

$-\dfrac{\pi}{3}+\dfrac{4\pi}{2}=-\dfrac{\pi}{3}+2\pi$

Alors, nous allons placer les points

$A\;,\ B\;,\ C\$ et

$\ D$ d'abscisses curvilignes respectives :

$\dfrac{-\pi}{3}\;;\ \dfrac{\pi}{6}\;;\ \dfrac{2\pi}{3}\;;\ \dfrac{7\pi}{6}$

$\dfrac{\pi}{4}+k\pi\;,\ k$ entier relatif

En choisissant le sens positif puis, en remplaçant

$k$ successivement, par

$0\;;\ 1\;;\ \ldots\;;\$ jusqu'à une valeur égale à

$\dfrac{\pi}{4}+2\pi$ , on obtient :

$\dfrac{\pi}{4}+0\pi=\dfrac{\pi}{4}$

$\dfrac{\pi}{4}+\pi=\dfrac{5\pi}{4}$

$\dfrac{\pi}{4}+2\pi=\dfrac{\pi}{4}+2\pi$

Plaçons les points

$A\$ et

$\ B$ d'abscisses curvilignes respectives :

$\dfrac{\pi}{4}\;;\ \dfrac{5\pi}{4}$

Remarque

Le point d'abscisse curviligne

$\alpha+2\pi$ est confondu au point d'abscisse curviligne

$\alpha.$

Par ailleurs, on pouvait aussi choisir le sens négatif et remplacer

$k$ successivement, par

$0\;;\ -1\;;\ -2\;;\ \ldots\;;\$ jusqu'à une valeur égale à

$\alpha-2\pi.$

Cela conduirait toujours aux mêmes points.

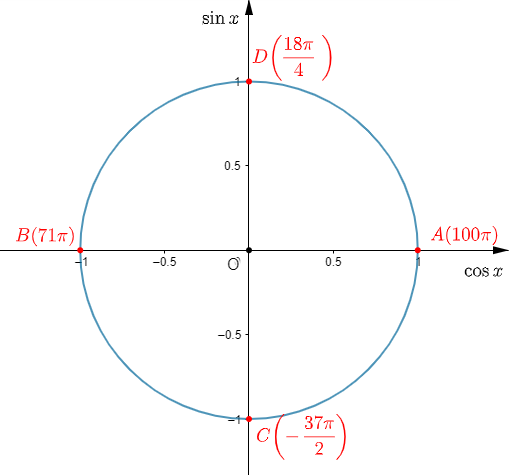
Exercice 9

Plaçons sur le cercle trigonométrique les points d'abscisses curvilignes :

$100\pi$

On a :

$100\pi=0+100\pi$

Donc,

$0$ est la mesure principale de

$100\pi.$

Par conséquent, le point d'abscisse curviligne

$100\pi$ est confondu au point d'abscisse curviligne

$0.$

On note alors

$A$ ce point.

$71\pi$

On a :

$71\pi=\pi+70\pi$

Donc,

$\pi$ est la mesure principale de

$71\pi.$

D'où, le point d'abscisse curviligne

$71\pi$ est confondu au point d'abscisse curviligne

$\pi.$

Soit alors

$B$ le point d'abscisse

$71\pi.$

$B$ est donc placé à l'abscisse curviligne

$\pi.$

$-\dfrac{37\pi}{2}$

Soit :

$-\dfrac{37\pi}{2}=-\dfrac{\pi}{2}-18\pi$

Alors,

$-\dfrac{\pi}{2}$ est la mesure principale de

$-\dfrac{37\pi}{2}.$

Par conséquent, le point

$C$ d'abscisse curviligne

$-\dfrac{37\pi}{2}$ sera placé au point d'abscisse curviligne

$-\dfrac{\pi}{2}.$

$\dfrac{18\pi}{4}$

On a :

$\dfrac{18\pi}{4}=\dfrac{2\pi}{4}+4\pi=\dfrac{\pi}{2}+4\pi$

Donc,

$\dfrac{\pi}{2}$ est la mesure principale de

$\dfrac{18\pi}{4}.$

Ainsi, le point

$D$ d'abscisse curviligne

$\dfrac{18\pi}{2}$ sera placé au point d'abscisse curviligne

$\dfrac{\pi}{2}.$

Exercice 10

Dans cet exercice, considérons

$\theta$ l'angle en radians et

$\alpha$ l'angle en degrés correspondant à

$\theta.$

Ainsi, comme dans l'exercice

$5$ , en appliquant les rapports de proportionnalité, on obtient :

$\dfrac{\theta}{\pi}=\dfrac{\alpha}{180}$

Ce qui entraine :

$\boxed{\theta=\dfrac{\alpha\times\pi}{180}\quad\text{et}\quad\alpha=\dfrac{\theta\times 180}{\pi}}$

Utilisons alors ces relations pour compléter le tableau suivant :

$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline \alpha\ (^{\circ})&45&30&60&15&18&75&135&90&60&36&22.5 \\ \hline\theta\ (\text{rad})&\pi/4&\pi/6&\pi/3&\pi/12&\pi/10&5\pi/12&3\pi/4&\pi/2&\pi/3&\pi/5&\pi/8 \\ \hline \alpha\ (^{\circ})&120&150&180&90&30&45&120&18&150&180&225 \\ \hline\theta\ (\text{rad})&2\pi/3&5\pi/6&\pi&\pi/2&\pi/6&\pi/4&2\pi/3&\pi/10&5\pi/6&\pi&5\pi/4 \\ \hline\end{array}$

Exercice 11

Pour chacune des mesures suivantes, déterminons :

$-\$ la mesure principale (en degré ou en radian, selon le cas) ;

$-\$ la mesure dans

$[0\;;\ 2\pi[$ (ou dans

$[0^{\circ}\;;\ 360^{\circ}[$ );

$-\$ la mesure dans

$[-2\pi\;;\ 0[$ (ou dans

$[-360^{\circ}\;;\ 0^{\circ}[$ ).

Les résultats sont alors regroupées dans le tableau suivant :

$\begin{array}{|c|c|c|c|}\hline\text{mesure}&\text{mesure principale}&\text{mesure dans }[0\;;\ 2\pi[&\text{mesure dans }[-2\pi\;;\ 0[\\&\text{en }(rad\text{ ou }deg)&\text{ou dans }[0^{\circ}\;;\ 360^{\circ}[&\text{ou dans }[-360^{\circ}\;;\ 0^{\circ}[\\\hline\dfrac{2008\pi}{3}&-\dfrac{2\pi}{3}&\dfrac{4\pi}{3}&-\dfrac{2\pi}{3}\\\hline\dfrac{28\pi}{5}&-\dfrac{2\pi}{5}&\dfrac{8\pi}{5}&-\dfrac{2\pi}{5}\\ \hline\dfrac{27\pi}{4}&\dfrac{3\pi}{4}&\dfrac{3\pi}{4}&-\dfrac{5\pi}{4}\\\hline-\dfrac{19\pi}{3}&-\dfrac{\pi}{3}&\dfrac{5\pi}{3}&-\dfrac{\pi}{3}\\\hline -270^{\circ}&90^{\circ}&90^{\circ}&-270^{\circ}\\\hline -18\pi&0&0&-2\pi\\\hline 1440^{\circ}&0^{\circ}&0^{\circ}&-360^{\circ}\\\hline -2530^{\circ}&-10^{\circ}&350^{\circ}&-10^{\circ}\\\hline -\dfrac{\pi}{4}&-\dfrac{\pi}{4}&\dfrac{7\pi}{4}&-\dfrac{\pi}{4}\\\hline\dfrac{5\pi}{6}&\dfrac{5\pi}{6}&\dfrac{5\pi}{6}&-\dfrac{7\pi}{6}\\\hline\dfrac{12\pi}{5}&\dfrac{2\pi}{5}&\dfrac{2\pi}{5}&-\dfrac{8\pi}{5}\\\hline -\dfrac{23\pi}{6}&\dfrac{\pi}{6}&\dfrac{\pi}{6}&-\dfrac{11\pi}{6}\\\hline 210^{\circ}&-150^{\circ}&210^{\circ}&-150^{\circ}\\\hline -375^{\circ}&-15^{\circ}&345^{\circ}&-15^{\circ}\\\hline -4512^{\circ}&168^{\circ}&168^{\circ}&-192^{\circ}\\\hline 17\pi&\pi&\pi&-\pi\\ \hline\end{array}$

En effet, en considérant

$x$ la mesure de l'angle en radian et

$\theta$ sa mesure principale alors, on a :

$\boxed{x=\theta+2k\pi\ \Rightarrow\ \theta=x-2k\pi}$

avec,

$k\in\mathbb{Z}\$ et

$\ \theta\in\;]-\pi\;;\ \pi]$

Donc, en procédant comme dans l'exercice

$1$ , on trouve

$k$ puis, on détermine

$\theta.$

On peut aussi déterminer

$\theta$ par calcul direct.

Par exemple, on a :

$\begin{array}{rcl}\dfrac{2008\pi}{3}&=&-\dfrac{2\pi}{3}+670\pi\\\\&=&-\dfrac{2\pi}{3}+2\times 335\pi\end{array}$

D'où,

$\boxed{\theta=-\dfrac{2\pi}{3}}$

De la même manière, on a :

$\begin{array}{rcl}-\dfrac{23\pi}{6}&=&\dfrac{\pi}{6}-4\pi\\\\&=&\dfrac{\pi}{6}-2\times 2\pi\end{array}$

Ainsi,

$\boxed{\theta=\dfrac{\pi}{6}}$

Pour déterminer la mesure dans

$[0\;;\ 2\pi[$ et celle dans

$[-2\pi\;;\ 0[$ , on procède comme suit :

$-\$ si

$\theta$ est positif alors, la mesure dans

$[0\;;\ 2\pi[$ est égale à

$\theta$ et la mesure dans

$[-2\pi\;;\ 0[$ est donnée par

$(\theta-2\pi)$

$-\$ si

$\theta$ est négatif alors, la mesure dans

$[0\;;\ 2\pi[$ est égale à

$(\theta+2\pi)$ et la mesure dans

$[-2\pi\;;\ 0[$ est

$\theta$

Par ailleurs, considérons

$y$ la mesure de l'angle en degré et

$\alpha$ sa mesure principale.

On obtient alors la relation suivante :

$\boxed{y=\alpha+k\times 360^{\circ}\ \Rightarrow\ \alpha=y-k\times 360^{\circ}}$

avec,

$k\in\mathbb{Z}\$ et

$\ \alpha\in\;]-180^{\circ}\;;\ 180^{\circ}]$

Par exemple, on a :

$\begin{array}{rcl}1440^{\circ}&=&0^{\circ}+1440^{\circ}\\\\&=&0^{\circ}+4\times 360^{\circ}\end{array}$

Donc,

$\boxed{\alpha=0^{\circ}}$

Encore, on a :

$\begin{array}{rcl}210^{\circ}&=&-150^{\circ}+360^{\circ}\end{array}$

D'où,

$\boxed{\alpha=-150^{\circ}}$

Pour déterminer la mesure dans

$[0^{\circ}\;;\ 360^{\circ}[$ et celle dans

$[-360^{\circ}\;;\ 0^{\circ}[$ , on adopte la méthode suivante :

$-\$ si

$\alpha$ est positif alors, la mesure dans

$[0^{\circ}\;;\ 360^{\circ}[$ est encore égale à

$\alpha$ et la mesure dans

$[-360^{\circ}\;;\ 0^{\circ}[$ est donnée par

$(\alpha-360^{\circ})$

$-\$ si

$\alpha$ est négatif alors, la mesure dans

$[0^{\circ}\;;\ 360^{\circ}[$ est donnée par

$(\alpha+360^{\circ})$ et la mesure dans

$[-360^{\circ}\;;\ 0^{\circ}[$ reste égale à

$\alpha$

Exercice 12

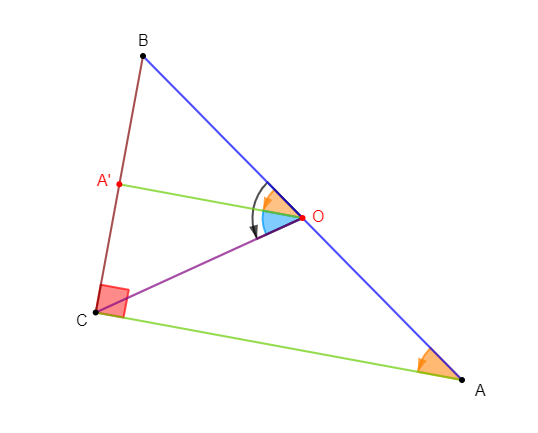
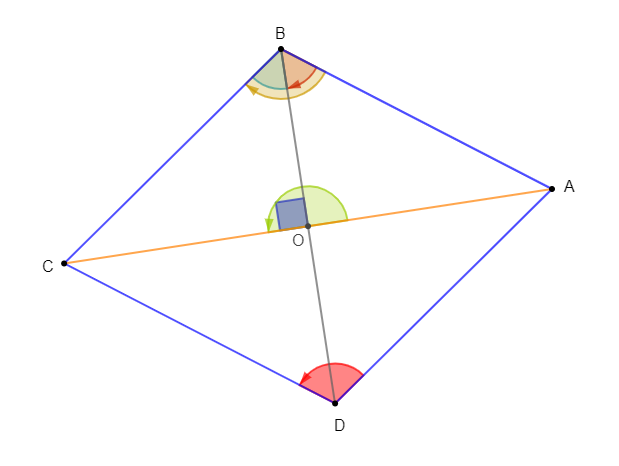
On considère un triangle

$ABC$ rectangle en

$C$ et tel que

$\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)=35^{\circ}$

Soit

$O\$ et

$\ A'$ les milieux respectifs des côtés

$[AB]\$ et

$\ [BC].$

Trouvons la mesure principale des angles orientés :

$\left(\overrightarrow{OB}\;,\ \overrightarrow{OA'}\right)\;;\ \left(\overrightarrow{OC}\;,\ \overrightarrow{OA'}\right)\;;\ \left(\overrightarrow{OA'}\;,\ \overrightarrow{OC}\right)\;;\ \left(\overrightarrow{OB}\;,\ \overrightarrow{OC}\right)$

$-\$ mesure principale de

$\left(\overrightarrow{OB}\;,\ \overrightarrow{OA'}\right)$

En effet,

$\left(\overrightarrow{OB}\;,\ \overrightarrow{OA'}\right)\$ et

$\ \left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)$ sont correspondants.

Or,

$O\$ et

$\ A'$ sont les milieux respectifs des côtés

$[AB]\$ et

$\ [BC].$

Donc, d'après le théorème de la droite des milieux, la droite

$(OA')$ est parallèle à la droite

$(AC).$

Par conséquent,

$\left(\overrightarrow{OB}\;,\ \overrightarrow{OA'}\right)\$ et

$\ \left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)$ ont même mesure.

D'où,

$\boxed{\left(\overrightarrow{OB}\;,\ \overrightarrow{OA'}\right)=35^{\circ}}$

$-\$ mesure principale de

$\left(\overrightarrow{OA'}\;,\ \overrightarrow{OC}\right)$

$ABC$ étant rectangle en

$C$ et

$O$ milieu de

$[AB]$ alors, le triangle

$COB$ est isocèle en

$O.$

Par conséquent,

$[OA')$ est la bissectrice de l'angle

$\widehat{O}.$

D'où,

$\left(\overrightarrow{OA'}\;,\ \overrightarrow{OC}\right)=\left(\overrightarrow{OB}\;,\ \overrightarrow{OA'}\right)$

Ainsi,

$\boxed{\left(\overrightarrow{OA'}\;,\ \overrightarrow{OC}\right)=35^{\circ}}$

$-\$ mesure principale de

$\left(\overrightarrow{OC}\;,\ \overrightarrow{OA'}\right)$

En effet, on sait que si

$\vec{u}\$ et

$\ \vec{v}$ sont deux vecteurs alors, on a :

$(\vec{u}\;;\ \vec{v})=-(\vec{v}\;;\ \vec{u})$

Ainsi, en appliquant cette propriété sur les angles orientés de vecteurs, on obtient :

$\left(\overrightarrow{OC}\;,\ \overrightarrow{OA'}\right)=-\left(\overrightarrow{OA'}\;,\ \overrightarrow{OC}\right)$

D'où,

$\boxed{\left(\overrightarrow{OC}\;,\ \overrightarrow{OA'}\right)=-35^{\circ}}$

$-\$ mesure principale de

$\left(\overrightarrow{OB}\;,\ \overrightarrow{OC}\right)$

D'après la relation de Chasles, on a :

$\begin{array}{rcl}\left(\overrightarrow{OB}\;,\ \overrightarrow{OC}\right)&=&\left(\overrightarrow{OB}\;,\ \overrightarrow{OA'}\right)+\left(\overrightarrow{OA'}\;,\ \overrightarrow{OC}\right)\\\\&=&35^{\circ}+35^{\circ}\\\\&=&70^{\circ}\end{array}$

D'où,

$\boxed{\left(\overrightarrow{OB}\;,\ \overrightarrow{OC}\right)=70^{\circ}}$

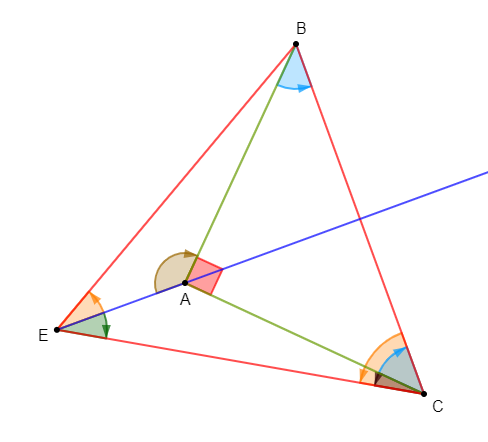
Exercice 13

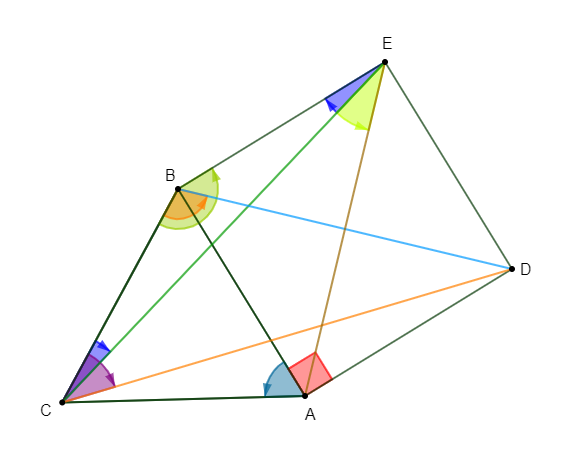
$ABC$ est un triangle équilatéral direct. On construit à l'extérieur le carré

$ABED.$

Déterminons les mesures principales en radians des angles orientés suivants :

$\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)\;;\ \left(\overrightarrow{AB}\;,\ \overrightarrow{AD}\right)\;;\ \left(\overrightarrow{BC}\;,\ \overrightarrow{BE}\right)\;,\ \left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)$

$\left(\overrightarrow{EC}\;,\ \overrightarrow{EB}\right)\;;\ \left(\overrightarrow{BC}\;,\ \overrightarrow{BD}\right)\;;\ \left(\overrightarrow{CB}\;,\ \overrightarrow{CD}\right)\;;\ \left(\overrightarrow{EC}\;,\ \overrightarrow{EA}\right)$

$-\$ mesure principale de

$\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)$

Le triangle

$ABC$ étant équilatéral alors, ses trois angles ont la même mesure principale.

D'où,

$\boxed{\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)=\dfrac{\pi}{3}}$

$-\$ mesure principale de

$\left(\overrightarrow{AB}\;,\ \overrightarrow{AD}\right)$

En appliquant une conséquence de la relation de Chasles sur les angles orientés de vecteurs, on obtient :

$\left(\overrightarrow{AB}\;,\ \overrightarrow{AD}\right)=-\left(\overrightarrow{AD}\;,\ \overrightarrow{AB}\right)$

Or,

$\left(\overrightarrow{AD}\;,\ \overrightarrow{AB}\right)=\dfrac{\pi}{2}$

Donc,

$\boxed{\left(\overrightarrow{AB}\;,\ \overrightarrow{AD}\right)=-\dfrac{\pi}{2}}$

$-\$ mesure principale de

$\left(\overrightarrow{BC}\;,\ \overrightarrow{BE}\right)$

D'après la relation de Chasles, on a :

$\begin{array}{rcl}\left(\overrightarrow{BC}\;,\ \overrightarrow{BE}\right)&=&\left(\overrightarrow{BC}\;,\ \overrightarrow{BA}\right)+\left(\overrightarrow{BA}\;,\ \overrightarrow{BE}\right)\\\\&=&\dfrac{\pi}{3}+\dfrac{\pi}{2}\\\\&=&\dfrac{5\pi}{6}\end{array}$

Ainsi,

$\boxed{\left(\overrightarrow{BC}\;,\ \overrightarrow{BE}\right)=\dfrac{5\pi}{6}}$

$-\$ mesure principale de

$\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)$

En effet,

$ABED$ étant un carré de côté

$AB\$ et

$\ ABC$ équilatéral alors, on a :

$BC=BE$

Ce qui signifie que le triangle

$BCE$ est isocèle en

$B.$

Par conséquent, les angles

$\left(\overrightarrow{CE}\;,\ \overrightarrow{CB}\right)\$ et

$\ \left(\overrightarrow{EB}\;,\ \overrightarrow{EC}\right)$ ont même mesure principale.

Donc,

$\left(\overrightarrow{CE}\;,\ \overrightarrow{CB}\right)=\left(\overrightarrow{EB}\;,\ \overrightarrow{EC}\right)=-\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)$

Par ailleurs, on sait que la somme des angles d'un triangle est égale à

$\pi.$

Ce qui signifie :

$\left(\overrightarrow{BC}\;,\ \overrightarrow{BE}\right)+\left(\overrightarrow{CE}\;,\ \overrightarrow{CB}\right)+\left(\overrightarrow{EB}\;,\ \overrightarrow{EC}\right)=\pi$

Ainsi, en remplaçant

$\left(\overrightarrow{CE}\;,\ \overrightarrow{CB}\right)\$ et

$\ \left(\overrightarrow{EB}\;,\ \overrightarrow{EC}\right)$ par

$-\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)$ , on obtient :

$\begin{array}{rcl}\left(\overrightarrow{BC}\;,\ \overrightarrow{BE}\right)+\left(\overrightarrow{CE}\;,\ \overrightarrow{CB}\right)+\left(\overrightarrow{EB}\;,\ \overrightarrow{EC}\right)=\pi&\Leftrightarrow&\dfrac{5\pi}{6}-\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)-\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)=\pi\\\\&\Leftrightarrow&-2\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)=\pi-\dfrac{5\pi}{6}\\\\&\Leftrightarrow&\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)=-\dfrac{\dfrac{\pi}{6}}{2}\\\\&\Leftrightarrow&\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)=-\dfrac{\pi}{12}\end{array}$

D'où,

$\boxed{\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)=-\dfrac{\pi}{12}}$

$-\$ mesure principale de

$\left(\overrightarrow{EC}\;,\ \overrightarrow{EB}\right)$

En effet,

$BCE$ étant isocèle en

$B$ alors, on a :

$\left(\overrightarrow{EC}\;,\ \overrightarrow{EB}\right)=\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)$

Or, d'après le résultat précédent, on a :

$\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)=-\dfrac{\pi}{12}.$

Par conséquent,

$\boxed{\left(\overrightarrow{EC}\;,\ \overrightarrow{EB}\right)=-\dfrac{\pi}{12}}$

$-\$ mesure principale de

$\left(\overrightarrow{BC}\;,\ \overrightarrow{BD}\right)$

D'après la relation de Chasles, on a :

$\left(\overrightarrow{BC}\;,\ \overrightarrow{BD}\right)=\left(\overrightarrow{BC}\;,\ \overrightarrow{BA}\right)+\left(\overrightarrow{BA}\;,\ \overrightarrow{BD}\right)$

Comme

$ABED$ est un carré alors, la diagonale

$[BD]$ est aussi bissectrice de l'angle

$\left(\overrightarrow{BA}\;,\ \overrightarrow{BE}\right).$

Par conséquent,

$\left(\overrightarrow{BA}\;,\ \overrightarrow{BD}\right)=\dfrac{\left(\overrightarrow{BA}\;,\ \overrightarrow{BE}\right)}{2}=\dfrac{\pi}{4}$

Ainsi, on a :

$\begin{array}{rcl}\left(\overrightarrow{BC}\;,\ \overrightarrow{BD}\right)&=&\left(\overrightarrow{BC}\;,\ \overrightarrow{BA}\right)+\left(\overrightarrow{BA}\;,\ \overrightarrow{BD}\right)\\\\&=&\dfrac{\pi}{3}+\dfrac{\pi}{4}\\\\&=&\dfrac{7\pi}{12}\end{array}$

D'où,

$\boxed{\left(\overrightarrow{BC}\;,\ \overrightarrow{BD}\right)=\dfrac{7\pi}{12}}$

$-\$ mesure principale de

$\left(\overrightarrow{CB}\;,\ \overrightarrow{CD}\right)$

D'après la relation de Chasles, on a :

$\left(\overrightarrow{CB}\;,\ \overrightarrow{CA}\right)=\left(\overrightarrow{CB}\;,\ \overrightarrow{CD}\right)+\left(\overrightarrow{CD}\;,\ \overrightarrow{CA}\right)$

Ce qui entraine :

$\left(\overrightarrow{CB}\;,\ \overrightarrow{CD}\right)=\left(\overrightarrow{CB}\;,\ \overrightarrow{CA}\right)-\left(\overrightarrow{CD}\;,\ \overrightarrow{CA}\right)$

Or, on sait que les triangles

$BCE\$ et

$\ ACD$ sont superposables donc, semblables.

Par conséquent,

$\left(\overrightarrow{CD}\;,\ \overrightarrow{CA}\right)=\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)$

Par suite, on obtient :

$\begin{array}{rcl}\left(\overrightarrow{CB}\;,\ \overrightarrow{CD}\right)&=&\left(\overrightarrow{CB}\;,\ \overrightarrow{CA}\right)-\left(\overrightarrow{CD}\;,\ \overrightarrow{CA}\right)\\\\&=&\left(\overrightarrow{CB}\;,\ \overrightarrow{CA}\right)-\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)\\\\&=&-\dfrac{\pi}{3}-\left(-\dfrac{\pi}{12}\right)\\\\&=&-\dfrac{\pi}{3}+\dfrac{\pi}{12}\\\\&=&-\dfrac{4\pi}{12}+\dfrac{\pi}{12}\\\\&=&-\dfrac{3\pi}{12}\\\\&=&-\dfrac{\pi}{4}\end{array}$

Ainsi,

$\boxed{\left(\overrightarrow{CB}\;,\ \overrightarrow{CD}\right)=-\dfrac{\pi}{4}}$

$-\$ mesure principale de

$\left(\overrightarrow{EC}\;,\ \overrightarrow{EA}\right)$

D'après la relation de Chasles, on a :

$\begin{array}{rcl}\left(\overrightarrow{EB}\;,\ \overrightarrow{EA}\right)=\left(\overrightarrow{EB}\;,\ \overrightarrow{EC}\right)+\left(\overrightarrow{EC}\;,\ \overrightarrow{EA}\right)&\Rightarrow&\left(\overrightarrow{EC}\;,\ \overrightarrow{EA}\right)=\left(\overrightarrow{EB}\;,\ \overrightarrow{EA}\right)-\left(\overrightarrow{EB}\;,\ \overrightarrow{EC}\right)\\\\&\Rightarrow&\left(\overrightarrow{EC}\;,\ \overrightarrow{EA}\right)=\left(\overrightarrow{EB}\;,\ \overrightarrow{EA}\right)+\left(\overrightarrow{EC}\;,\ \overrightarrow{EB}\right)\end{array}$

Ainsi, on trouve :

$\begin{array}{rcl}\left(\overrightarrow{EC}\;,\ \overrightarrow{EA}\right)&=&\left(\overrightarrow{EB}\;,\ \overrightarrow{EA}\right)+\left(\overrightarrow{EC}\;,\ \overrightarrow{EB}\right)\\\\&=&\dfrac{\pi}{4}-\dfrac{\pi}{12}\\\\&=&\dfrac{3\pi}{12}-\dfrac{\pi}{12}\\\\&=&\dfrac{2\pi}{12}\\\\&=&\dfrac{\pi}{6}\end{array}$

D'où,

$\boxed{\left(\overrightarrow{EC}\;,\ \overrightarrow{EA}\right)=\dfrac{\pi}{6}}$

Remarque

$ABC$ étant direct alors, cela signifie que pour construire ce triangle

$ABC$ , on part de

$A$ vers

$B$ en suivant le sens positif.

Exercice 14

On considère un losange

$ABCD$ dont les diagonales se coupent en

$O$ et tel que :

$\left(\overrightarrow{BA}\;,\ \overrightarrow{BD}\right)=-54^{\circ}$

Déterminons les mesures principales en radians des angles orientés suivants :

$\left(\overrightarrow{BA}\;,\ \overrightarrow{BD}\right)\;;\ \left(\overrightarrow{BC}\;,\ \overrightarrow{BD}\right)\;;\ \left(\overrightarrow{BD}\;,\ \overrightarrow{BC}\right)\;;\ \left(\overrightarrow{BA}\;,\ \overrightarrow{BC}\right)$

$\left(\overrightarrow{DA}\;,\ \overrightarrow{DC}\right)\;;\ \left(\overrightarrow{OC}\;,\ \overrightarrow{OB}\right)\;;\ \left(\overrightarrow{OA}\;,\ \overrightarrow{OC}\right)$

$-\$ mesure principale de

$\left(\overrightarrow{BA}\;,\ \overrightarrow{BD}\right)$

D'après les données de l'exercice, on a :

$\left(\overrightarrow{BA}\;,\ \overrightarrow{BD}\right)=-54^{\circ}$

Convertissons alors cette mesure en radians.

En effet, on sait que si

$\alpha$ est un angle en degrés et

$\theta$ l'angle en radians correspondant à

$\alpha$ alors, on a la relation suivante :

$\theta=\dfrac{\alpha\times\pi}{180}$

Ainsi, en appliquant cette propriété à l'angle

$\left(\overrightarrow{BA}\;,\ \overrightarrow{BD}\right)$ , on trouve :

$\begin{array}{rcl}\left(\overrightarrow{BA}\;,\ \overrightarrow{BD}\right)&=&\dfrac{-54\times\pi}{180}\\\\&=&-\dfrac{18\times 3\pi}{18\times 10}\\\\&=&-\dfrac{3\pi}{10}\end{array}$

D'où,

$\boxed{\left(\overrightarrow{BA}\;,\ \overrightarrow{BD}\right)=-\dfrac{3\pi}{10}}$

$-\$ mesure principale de

$\left(\overrightarrow{BC}\;,\ \overrightarrow{BD}\right)$

$ABCD$ étant un losange alors, la diagonale

$[BD]$ est aussi bissectrice de l'angle

$\left(\overrightarrow{BC}\;,\ \overrightarrow{BA}\right)$

Par conséquent,

$\left(\overrightarrow{BC}\;,\ \overrightarrow{BD}\right)=\left(\overrightarrow{BD}\;,\ \overrightarrow{BA}\right)$

Or, d'après les propriétés sur les angles orientés de vecteurs, on a :

$\left(\overrightarrow{BD}\;,\ \overrightarrow{BA}\right)=-\left(\overrightarrow{BA}\;,\ \overrightarrow{BD}\right)$

Ainsi, d'après le résultat précédent, on trouve :

$\begin{array}{rcl}\left(\overrightarrow{BC}\;,\ \overrightarrow{BD}\right)&=&-\left(\overrightarrow{BA}\;,\ \overrightarrow{BD}\right)\\\\&=&-\left(-\dfrac{3\pi}{10}\right)\\\\&=&\dfrac{3\pi}{10}\end{array}$

D'où,

$\boxed{\left(\overrightarrow{BC}\;,\ \overrightarrow{BD}\right)=\dfrac{3\pi}{10}}$

$-\$ mesure principale de

$\left(\overrightarrow{BD}\;,\ \overrightarrow{BC}\right)$

D"après les propriétés sur les angles orientés de vecteurs, on a :

$\left(\overrightarrow{BD}\;,\ \overrightarrow{BC}\right)=-\left(\overrightarrow{BC}\;,\ \overrightarrow{BD}\right)$

Or, d'après le résultat précédent,

$\left(\overrightarrow{BC}\;,\ \overrightarrow{BD}\right)=\dfrac{3\pi}{10}$

Par conséquent,

$\boxed{\left(\overrightarrow{BD}\;,\ \overrightarrow{BC}\right)=-\dfrac{3\pi}{10}}$

$-\$ mesure principale de

$\left(\overrightarrow{BA}\;,\ \overrightarrow{BC}\right)$

D'après la relation de Chasles, on a :

$\begin{array}{rcl}\left(\overrightarrow{BA}\;,\ \overrightarrow{BC}\right)&=&\left(\overrightarrow{BA}\;,\ \overrightarrow{BD}\right)+\left(\overrightarrow{BD}\;,\ \overrightarrow{BC}\right)\\\\&=&-\dfrac{3\pi}{10}-\dfrac{3\pi}{10}\\\\&=&-\dfrac{6\pi}{10}\\\\&=&-\dfrac{3\pi}{5}\end{array}$

D'où,

$\boxed{\left(\overrightarrow{BA}\;,\ \overrightarrow{BC}\right)=-\dfrac{3\pi}{5}}$

$-\$ mesure principale de

$\left(\overrightarrow{DA}\;,\ \overrightarrow{DC}\right)$

En effet, dans un parallélogramme, deux angles opposés ont même mesures.

Donc,

$\left(\overrightarrow{DA}\;,\ \overrightarrow{DC}\right)=\left(\overrightarrow{BC}\;,\ \overrightarrow{BA}\right)$

Or, d'après les propriétés sur les angles orientés de vecteurs, on a :

$\left(\overrightarrow{BC}\;,\ \overrightarrow{BA}\right)=-\left(\overrightarrow{BA}\;,\ \overrightarrow{BC}\right)$

Par suite, on obtient :

$\begin{array}{rcl}\left(\overrightarrow{DA}\;,\ \overrightarrow{DC}\right)&=&-\left(\overrightarrow{BA}\;,\ \overrightarrow{BC}\right)\\\\&=&-\left(-\dfrac{3\pi}{5}\right)\\\\&=&\dfrac{3\pi}{5}\end{array}$

Ainsi,

$\boxed{\left(\overrightarrow{DA}\;,\ \overrightarrow{DC}\right)=\dfrac{3\pi}{5}}$

$-\$ mesure principale de

$\left(\overrightarrow{OC}\;,\ \overrightarrow{OB}\right)$

Comme

$ABCD$ est un losange alors, les diagonales

$(BD)\$ et

$\ (AC)$ sont perpendiculaires en

$O.$

Par conséquent,

$\boxed{\left(\overrightarrow{OC}\;,\ \overrightarrow{OB}\right)=-\dfrac{\pi}{2}}$

$-\$ mesure principale de

$\left(\overrightarrow{OA}\;,\ \overrightarrow{OC}\right)$

$O$ étant milieu de

$[AC]$ alors, on a :

$\overrightarrow{OA}=-\overrightarrow{OC}$

Ainsi,

$\left(\overrightarrow{OA}\;,\ \overrightarrow{OC}\right)=\left(-\overrightarrow{OC}\;,\ \overrightarrow{OC}\right)$

Or, d'après les propriétés sur les angles orientés de vecteurs, on a :

$\left(-\overrightarrow{OC}\;,\ \overrightarrow{OC}\right)=\pi$

D'où,

$\boxed{\left(\overrightarrow{OA}\;,\ \overrightarrow{OC}\right)=\pi}$

Exercice 15

$ABC$ est un triangle rectangle isocèle en

$A$ de sens indirect. On construit le triangle équilatéral

$BCE$ de manière que

$E$ appartienne au demi-plan de frontière

$(BC)$ contenant

$A.$

Déterminons les mesures principales en radians des angles orientés suivants :

$\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)\;;\ \left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)\;;\ \left(\overrightarrow{CA}\;,\ \overrightarrow{CB}\right)\;;\ \left(\overrightarrow{BA}\;,\ \overrightarrow{BC}\right)$

$\left(\overrightarrow{EA}\;,\ \overrightarrow{EC}\right)\;;\ \left(\overrightarrow{CA}\;,\ \overrightarrow{CE}\right)\;;\ \left(\overrightarrow{EA}\;,\ \overrightarrow{EB}\right)\;;\ \left(\overrightarrow{AE}\;,\ \overrightarrow{AB}\right)$

Remarque

$ABC$ étant de sens indirect alors, cela signifie que pour construire le triangle

$ABC$ , on part de

$A$ vers

$B$ en suivant le sens négatif qui correspond au sens des aiguilles d'une montre.

$-\$ mesure principale de

$\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)$

On sait que

$ABC$ est un triangle rectangle isocèle en

$A$ de sens indirect.

Par conséquent,

$\boxed{\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)=-\dfrac{\pi}{2}}$

$-\$ mesure principale de

$\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)$

Comme

$BCE$ est un triangle équilatéral alors,

$\boxed{\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)=\dfrac{\pi}{3}}$

$-\$ mesure principale de

$\left(\overrightarrow{CA}\;,\ \overrightarrow{CB}\right)$

$ABC$ étant un triangle rectangle isocèle en

$A$ donc,

$\boxed{\left(\overrightarrow{CA}\;,\ \overrightarrow{CB}\right)=-\dfrac{\pi}{4}}$

$-\$ mesure principale de

$\left(\overrightarrow{BA}\;,\ \overrightarrow{BC}\right)$

Comme

$ABC$ étant un triangle isocèle en

$A$ alors, on a :

$\left(\overrightarrow{BA}\;,\ \overrightarrow{BC}\right)=\left(\overrightarrow{CB}\;,\ \overrightarrow{CA}\right)$

Or, d'après les propriétés sur les angles orientés de vecteurs, on a :

$\left(\overrightarrow{CB}\;,\ \overrightarrow{CA}\right)=-\left(\overrightarrow{CA}\;,\ \overrightarrow{CB}\right)$

Ainsi, on trouve :

$\begin{array}{rcl}\left(\overrightarrow{BA}\;,\ \overrightarrow{BC}\right)&=&-\left(\overrightarrow{CA}\;,\ \overrightarrow{CB}\right)\\\\&=&-\left(-\dfrac{\pi}{4}\right)\\\\&=&\dfrac{\pi}{4}\end{array}$

D'où,

$\boxed{\left(\overrightarrow{BA}\;,\ \overrightarrow{BC}\right)=\dfrac{\pi}{4}}$

$-\$ mesure principale de

$\left(\overrightarrow{EA}\;,\ \overrightarrow{EC}\right)$

En effet, comme

$ABC$ est rectangle isocèle en

$A\$ et

$BCE$ équilatéral alors,

$[EA)$ est une bissectrice des angles orientés

$\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)\$ et

$\ \left(\overrightarrow{EB}\;,\ \overrightarrow{EC}\right).$

Donc, on obtient :

$\begin{array}{rcl}\left(\overrightarrow{EA}\;,\ \overrightarrow{EC}\right)&=&\dfrac{\left(\overrightarrow{EB}\;,\ \overrightarrow{EC}\right)}{2}\\\\&=&\dfrac{-\dfrac{\pi}{3}}{2}\\\\&=&-\dfrac{\pi}{6}\end{array}$

Ainsi,

$\boxed{\left(\overrightarrow{EA}\;,\ \overrightarrow{EC}\right)=-\dfrac{\pi}{6}}$

$-\$ mesure principale de

$\left(\overrightarrow{CA}\;,\ \overrightarrow{CE}\right)$

D'après la relation de Chasles, on a :

$\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)=\left(\overrightarrow{CB}\;,\ \overrightarrow{CA}\right)+\left(\overrightarrow{CA}\;,\ \overrightarrow{CE}\right)$

Ce qui entraine alors :

$\begin{array}{rcl}\left(\overrightarrow{CA}\;,\ \overrightarrow{CE}\right)&=&\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)-\left(\overrightarrow{CB}\;,\ \overrightarrow{CA}\right)\\\\&=&\left(\overrightarrow{CB}\;,\ \overrightarrow{CE}\right)+\left(\overrightarrow{CA}\;,\ \overrightarrow{CB}\right)\\\\&=&\dfrac{\pi}{3}-\dfrac{\pi}{4}\\\\&=&\dfrac{4\pi}{12}-\dfrac{3\pi}{12}\\\\&=&\dfrac{\pi}{12}\end{array}$

D'où,

$\boxed{\left(\overrightarrow{CA}\;,\ \overrightarrow{CE}\right)=\dfrac{\pi}{12}}$

$-\$ mesure principale de

$\left(\overrightarrow{EA}\;,\ \overrightarrow{EB}\right)$

$[EA)$ étant la bissectrice de l'angle orienté

$\left(\overrightarrow{EB}\;,\ \overrightarrow{EC}\right)$ alors, on a :

$\left(\overrightarrow{EA}\;,\ \overrightarrow{EB}\right)=-\left(\overrightarrow{EA}\;,\ \overrightarrow{EC}\right)$

Or, d'après les résultats précédents, on a :

$\left(\overrightarrow{EA}\;,\ \overrightarrow{EC}\right)=-\dfrac{\pi}{6}$

Par conséquent,

$\boxed{\left(\overrightarrow{EA}\;,\ \overrightarrow{EB}\right)=\dfrac{\pi}{6}}$

$-\$ mesure principale de

$\left(\overrightarrow{AE}\;,\ \overrightarrow{AB}\right)$

En effet, en utilisant la relation de Chasles, on obtient :

$\left(\overrightarrow{AE}\;,\ -\overrightarrow{AE}\right)=\left(\overrightarrow{AE}\;,\ \overrightarrow{AB}\right)+\left(\overrightarrow{AB}\;,\ -\overrightarrow{AE}\right)$

Ce qui donne alors :

$\left(\overrightarrow{AE}\;,\ \overrightarrow{AB}\right)=\left(\overrightarrow{AE}\;,\ -\overrightarrow{AE}\right)-\left(\overrightarrow{AB}\;,\ -\overrightarrow{AE}\right)$

Or, d'après les propriétés sur les angles orientés de vecteurs, on a :

$\left(\overrightarrow{AE}\;,\ -\overrightarrow{AE}\right)=-\pi$

De plus,

$[EA)$ étant bissectrice de

$\left(\overrightarrow{AB}\;,\ \overrightarrow{AC}\right)$ alors, on a :

$\left(\overrightarrow{AB}\;,\ -\overrightarrow{AE}\right)=-\dfrac{\pi}{4}$

Par suite, on trouve :

$\begin{array}{rcl}\left(\overrightarrow{AE}\;,\ \overrightarrow{AB}\right)&=&\left(\overrightarrow{AE}\;,\ -\overrightarrow{AE}\right)-\left(\overrightarrow{AB}\;,\ -\overrightarrow{AE}\right)\\\\&=&-\pi-\left(-\dfrac{\pi}{4}\right)\\\\&=&-\dfrac{4\pi}{4}+\dfrac{\pi}{4}\\\\&=&-\dfrac{3\pi}{4}\end{array}$

Par conséquent,

$\boxed{\left(\overrightarrow{AE}\;,\ \overrightarrow{AB}\right)=-\dfrac{3\pi}{4}}$

Exercice 16

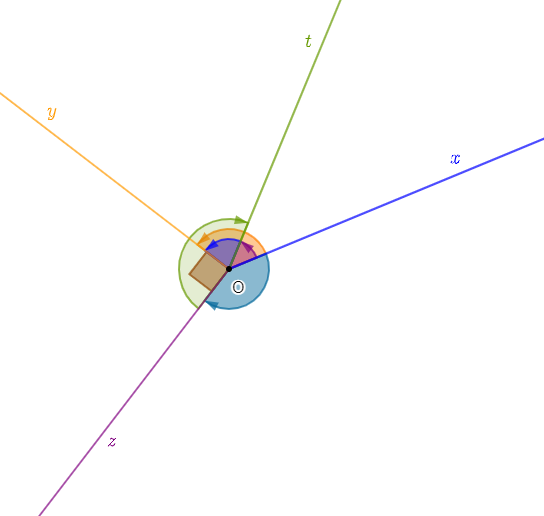
On donne dans le plan orienté

$P$ , une demi-droite

$Ox.$

1) Construisons les demi-droites

$Oy\;,\ Oz\;,\ Ot$ telles que :

$\left(Ox\;,\ Oy\right)=\dfrac{2\pi}{3}\;,\quad\left(Ox\;,\ Oz\right)=-\dfrac{5\pi}{6}\;,\quad\left(Ox\;,\ Ot\right)=\dfrac{\pi}{4}$

2) Calculons la mesure principale en radians des angles orientés suivants :

$\left(Oy\;,\ Oz\right)\;,\ \left(Oz\;,\ Ot\right)\;,\ \left(Ot\;,\ Oy\right)$

$-\$ mesure principale de

$\left(Oy\;,\ Oz\right)$

En effet, en utilisant la relation de Chasles, on obtient :

$\left(Oy\;,\ Oz\right)=\left(Oy\;,\ Ox\right)+\left(Ox\;,\ Oz\right)$

Or, d'après les propriétés sur les angles orientés de demi-droites, on a :

$\left(Oy\;,\ Ox\right)=-\left(Ox\;,\ Oy\right)$

Ainsi, on trouve :

$\begin{array}{rcl}\left(Oy\;,\ Oz\right)&=&\left(Oy\;,\ Ox\right)+\left(Ox\;,\ Oz\right)\\\\&=&-\left(Ox\;,\ Oy\right)+\left(Ox\;,\ Oz\right)\\\\&=&-\dfrac{2\pi}{3}-\dfrac{5\pi}{6}\\\\&=&-\dfrac{4\pi}{6}-\dfrac{5\pi}{6}\\\\&=&-\dfrac{9\pi}{6}\\\\&=&\dfrac{3\pi}{6}-2\pi\\\\&=&\dfrac{\pi}{2}-2\pi\end{array}$

Par conséquent, la mesure principale en radians de l'angle orienté

$\left(Oy\;,\ Oz\right)$ est donnée par :

$\boxed{\left(Oy\;,\ Oz\right)=\dfrac{\pi}{2}}$

$-\$ mesure principale de

$\left(Oz\;,\ Ot\right)$

D'après la relation de Chasles, on a :

$\left(Oz\;,\ Ot\right)=\left(Oz\;,\ Ox\right)+\left(Ox\;,\ Ot\right)$

Comme

$\left(Oz\;,\ Ox\right)=-\left(Ox\;,\ Oz\right)$ alors, on obtient :

$\begin{array}{rcl}\left(Oz\;,\ Ot\right)&=&\left(Oz\;,\ Ox\right)+\left(Ox\;,\ Ot\right)\\\\&=&-\left(Ox\;,\ Oz\right)+\left(Ox\;,\ Ot\right)\\\\&=&-\left(-\dfrac{5\pi}{6}\right)+\dfrac{\pi}{4}\\\\&=&\dfrac{5\pi}{6}+\dfrac{\pi}{4}\\\\&=&\dfrac{10\pi}{12}+\dfrac{3\pi}{12}\\\\&=&\dfrac{13\pi}{12}\\\\&=&-\dfrac{11\pi}{12}+2\pi\end{array}$

D'où, la mesure principale en radians de l'angle orienté

$\left(Oz\;,\ Ot\right)$ est donnée par :

$\boxed{\left(Oz\;,\ Ot\right)=-\dfrac{11\pi}{12}}$

$-\$ mesure principale de

$\left(Ot\;,\ Oy\right)$

En utilisant encore la relation de Chasles, on obtient :

$\left(Ot\;,\ Oy\right)=\left(Ot\;,\ Ox\right)+\left(Ox\;,\ Oy\right)$

Or, d'après les propriétés sur les angles orientés de demi-droites, on a :

$\left(Ot\;,\ Ox\right)=-\left(Ox\;,\ Ot\right)$

On peut alors écrire :

$\begin{array}{rcl}\left(Ot\;,\ Oy\right)&=&\left(Ot\;,\ Ox\right)+\left(Ox\;,\ Oy\right)\\\\&=&-\left(Ox\;,\ Ot\right)+\left(Ox\;,\ Oy\right)\\\\&=&-\dfrac{\pi}{4}+\dfrac{2\pi}{3}\\\\&=&-\dfrac{3\pi}{12}+\dfrac{8\pi}{12}\\\\&=&\dfrac{5\pi}{12}\end{array}$

D'où, on trouve :

$\boxed{\left(Ot\;,\ Oy\right)=\dfrac{5\pi}{12}}$

Exercice 21

Démontrons que, pour tout réel

$t\ :$

$(\cos t+\sin t)^{2}=1+2\cos t\sin t$

En utilisant la forme développée des identités remarquables, on obtient :

$\begin{array}{rcl}(\cos t+\sin t)^{2}&=&\cos^{2}t+2\cos t\sin t+\sin^{2}t\\\\&=&\underbrace{\cos^{2}t+\sin^{2}t}_{=1}+2\cos t\sin t\\\\&=&1+2\cos t\sin t\end{array}$

D'où,

$\boxed{(\cos t+\sin t)^{2}=1+2\cos t\sin t}$

$(\cos t-\sin t)^{2}=1-2\cos t\sin t$

D'après la forme développée des identités remarquables, on a :

$\begin{array}{rcl}(\cos t-\sin t)^{2}&=&\cos^{2}t-2\cos t\sin t+\sin^{2}t\\\\&=&\underbrace{\cos^{2}t+\sin^{2}t}_{=1}-2\cos t\sin t\\\\&=&1-2\cos t\sin t\end{array}$

Ainsi,

$\boxed{(\cos t-\sin t)^{2}=1-2\cos t\sin t}$

$(\cos t+\sin t)^{2}+(\cos t-\sin t)^{2}=2$

En effet, d'après les résultats des questions

$1\,)\$ et

$\ 2\,)$ , on a :

$\cos t+\sin t)^{2}=1+2\cos t\sin t\qquad(1)$

$\cos t-\sin t)^{2}=1-2\cos t\sin t\qquad(2)$

Alors, en additionnant, membre à membre, les relations

$(1)\$ et

$\ (2)$ , on obtient :

$\begin{array}{rcl}(\cos t+\sin t)^{2}+(\cos t-\sin t)^{2}&=&(1+2\cos t\sin t)+(1-2\cos t\sin t)\\\\&=&1+2\cos t\sin t+1-2\cos t\sin t\\\\&=&2\end{array}$

D'où,

$\boxed{(\cos t+\sin t)^{2}+(\cos t-\sin t)^{2}=2}$

$(\cos t+\sin t)^{2}-(\cos t-\sin t)^{2}=4\sin t\cos t$

En utilisant les résultats des questions

$1\,)\$ et

$\ 2\,)$ , on trouve :

$\begin{array}{rcl}(\cos t+\sin t)^{2}-(\cos t-\sin t)^{2}&=&(1+2\cos t\sin t)-(1-2\cos t\sin t)\\\\&=&1+2\cos t\sin t-1+2\cos t\sin t\\\\&=&4\cos t\sin t\end{array}$

D'où,

$\boxed{(\cos t+\sin t)^{2}-(\cos t-\sin t)^{2}=4\sin t\cos t}$

$\sin^{4}t-\cos^{4}t=\sin^{2}t-\cos^{2}t$

En effet, en utilisant la forme factorisée des identités remarquables, on a :

$\sin^{4}t-\cos^{4}t=\left(\sin^{2}t-\cos^{2}t\right)\left(\sin^{2}t+\cos^{2}t\right)$

Or, on sait que :

$\sin^{2}t+\cos^{2}t=1$

Par conséquent,

$\boxed{\sin^{4}t-\cos^{4}t=\sin^{2}t-\cos^{2}t}$

$\sin^{4}t-\cos^{4}t+2\cos^{2}t=1$

D'après le résultat de la question

$5\,)$ , on a :

$\sin^{4}t-\cos^{4}t=\sin^{2}t-\cos^{2}t$

Or, on sait que :

$\sin^{2}t=1-\cos^{2}t$

Donc, en remplaçant, on obtient :

$\begin{array}{rcl}\sin^{4}t-\cos^{4}t+2\cos^{2}t&=&\sin^{2}t-\cos^{2}t+2\cos^{2}t\\\\&=&1-\cos^{2}t-\cos^{2}t+2\cos^{2}t\\\\&=&1-2\cos^{2}t+2\cos^{2}t\\\\&=&1\end{array}$

D'où,

$\boxed{\sin^{4}t-\cos^{4}t+2\cos^{2}t=1}$

Exercice 22

Exprimons en fonction de

$\sin t\$ et

$\ \cos t$ les expressions suivantes :

Soit

$A=\cos(t+\pi)+\cos(t+2\pi)+\cos(t-\pi)+\cos(t-3\pi)$

Alors, en utilisant les propriétés trigonométriques du sinus et du cosinus, on trouve :

$\begin{array}{rcl} A&=&\cos(t+\pi)+\cos(t+2\pi)+\cos(t-\pi)+\cos(t-3\pi)\\\\&=&-\cos t+\cos t-\cos t+\cos[(t-\pi)-2\pi]\\\\&=&-\cos t+\cos(t-\pi)\\\\&=&-\cos t-\cos t\\\\&=&-2\cos t\end{array}$

D'où,

$\boxed{A=-2\cos t}$

Soit :

$B=\sin(t+\pi)+\sin(t+2\pi)+\sin(t-\pi)+\sin(t-3\pi)$

Alors, en utilisant les propriétés trigonométriques du sinus et du cosinus, on obtient :

$\begin{array}{rcl} B&=&\sin(t+\pi)+\sin(t+2\pi)+\sin(t-\pi)+\sin(t-3\pi)\\\\&=&-\sin t+\sin t-\sin t+\sin[(t-\pi)-2\pi]\\\\&=&-\sin t+\sin(t-\pi)\\\\&=&-\sin t-\sin t\\\\&=&-2\sin t\end{array}$

Ainsi,

$\boxed{B=-2\sin t}$

Soit :

$C=\sin\left(t+\dfrac{\pi}{2}\right)+\cos(t-\pi)+\sin\left(t+\dfrac{3\pi}{2}\right)+\cos(t+\pi)$

Alors, d'après les propriétés trigonométriques du sinus et du cosinus, on a :

$\begin{array}{rcl} C&=&\sin\left(t+\dfrac{\pi}{2}\right)+\cos(t-\pi)+\sin\left(t+\dfrac{3\pi}{2}\right)+\cos(t+\pi)\\\\&=&\cos t-\cos t+\sin\left[\left(t+\dfrac{\pi}{2}\right)+\pi\right]-\cos t\\\\&=&-\sin\left(t+\dfrac{\pi}{2}\right)-\cos t\\\\&=&-\cos t-\cos t\\\\&=&-2\cos t\end{array}$

D'où,

$\boxed{C=-2\cos t}$

Soit :

$D=\sin\left(\dfrac{3\pi}{2}+t\right)+\cos\left(\dfrac{27\pi}{2}-t\right)+\sin(3\pi+t)-\cos(7\pi-t)$

Alors, en utilisant les propriétés trigonométriques du sinus et du cosinus, on obtient :

$\begin{array}{rcl} D&=&\sin\left(\dfrac{3\pi}{2}+t\right)+\cos\left(\dfrac{27\pi}{2}-t\right)+\sin(3\pi+t)-\cos(7\pi-t)\\\\&=&\sin\left[\pi+\left(\dfrac{\pi}{2}+t\right)\right]+\cos\left[14\pi+\left(-\dfrac{\pi}{2}-t\right)\right]+\sin[2\pi+(\pi+t)]-\cos[6\pi+(\pi-t)]\\\\&=&-\sin\left(\dfrac{\pi}{2}+t\right)+\cos\left(-\dfrac{\pi}{2}-t\right)+\sin(\pi+t)-\cos(\pi-t)\\\\&=&-\cos t+\cos\left[-\left(\dfrac{\pi}{2}+t\right)\right]-\sin t+\cos t\\\\&=&-\cos t+\cos t+\cos\left(\dfrac{\pi}{2}+t\right)-\sin t\\\\&=&-\sin t-\sin t\\\\&=&-2\sin t\end{array}$

D'où,

$\boxed{D=-2\sin t}$

Exercice 23

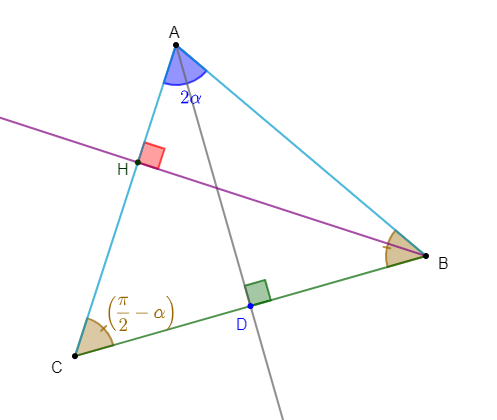
Soit

$ABC$ un triangle isocèle à angles aigus :

$AB=AC=a\;;\ \widehat{A}=2\alpha$

1) Calculons

$BC.$

Comme

$AB=AC=a$ alors,

$ABC$ est un triangle isocèle en

$A.$

Donc, la bissectrice

$[AD)$ de l'angle

$\widehat{BAC}$ est aussi médiatrice du segment

$[BC].$

Ainsi,

$ADB$ est un triangle rectangle au point

$D$ qui est le milieu de

$[BC].$

Par conséquent, en utilisant le sinus de l'angle

$\widehat{DAB}$ , on obtient :

$\begin{array}{rcl}\dfrac{BD}{AB}=\sin\widehat{DAB}&\Leftrightarrow&\dfrac{BD}{AB}=\sin\alpha\\\\&\Leftrightarrow&BD=AB\sin\alpha\\\\&\Leftrightarrow&\dfrac{BC}{2}=AB\sin\alpha\\\\&\Leftrightarrow&BC=2AB\sin\alpha\\\\&\Leftrightarrow&BC=2a\sin\alpha\end{array}$

D'où,

$\boxed{BC=2a\sin\alpha}$

2) Calculons la hauteur

$BH$ de deux façons différentes.

En effet,

$BH$ étant la hauteur issue de

$B$ alors,

$AHB$ est un triangle rectangle en

$H.$

Donc, en utilisant le sinus de l'angle

$\widehat{HAB}$ , on obtient :

$\begin{array}{rcl}\dfrac{BH}{AB}=\sin\widehat{HAB}&\Leftrightarrow&\dfrac{BH}{AB}=\sin 2\alpha\\\\&\Leftrightarrow&BH=AB\sin 2\alpha\\\\&\Leftrightarrow&BH=a\sin 2\alpha\end{array}$

Ainsi,

$\boxed{BH=a\sin 2\alpha\qquad(1)}$

Par ailleurs,

$CHB$ est aussi un triangle rectangle en

$H.$

Donc, en utilisons le sinus de l'angle

$\widehat{HCB}$ , on obtient :

$\dfrac{BH}{BC}=\sin\widehat{HCB}\ \Rightarrow\ BH=BC\sin\widehat{HCB}$

Ainsi, en remplaçant

$BC$ par son expression, on trouve une autre écriture de

$BH$ , donnée par :

$\boxed{BH=2a\sin\alpha\sin\widehat{HCB}}$

Déterminons alors la mesure de l'angle

$\widehat{HCB}.$

$ABC$ étant isocèle en

$A$ alors, on a :

$\widehat{ACB}=\widehat{CBA}$

Or, on sait que dans un tringle, la somme des mesures des angles est égale à

$\pi.$

De plus,

$\widehat{CAB}=2\alpha$

Donc, on a :

$\begin{array}{rcl}\widehat{ACB}+\widehat{CBA}+\widehat{CAB}=\pi&\Leftrightarrow&2\widehat{ACB}=\pi-\widehat{CAB}\\\\&\Leftrightarrow&\widehat{ACB}=\dfrac{\pi-2\alpha}{2}\\\\&\Leftrightarrow&\widehat{ACB}=\dfrac{\pi}{2}-\dfrac{2\alpha}{2}\\\\&\Leftrightarrow&\widehat{ACB}=\dfrac{\pi}{2}-\alpha\end{array}$

Ainsi,

$\boxed{\widehat{ACB}=\dfrac{\pi}{2}-\alpha}$

Par suite, en remplaçant cette valeur de l'angle

$\widehat{ACB}$ , dans l'expression de

$BH$ , on obtient :

$\begin{array}{rcl}BH&=&2a\sin\alpha\sin\widehat{HCB}\\\\&=&2a\sin\alpha\sin\left(\dfrac{\pi}{2}-\alpha\right)\\\\&=&2a\sin\alpha\cos\alpha\end{array}$

D'où,

$\boxed{BH=2a\sin\alpha\cos\alpha\qquad(2)}$

En déduisons la relation :

$\sin 2\alpha=2\sin\alpha\cos\alpha$

En comparant les égalités

$(1)\$ et

$\ (2)$ , on obtient :

$\begin{array}{rcl}\text{égalité }(1)=\text{égalité }(2)&\Leftrightarrow&a\sin 2\alpha=2a\sin\alpha\cos\alpha\\\\&\Leftrightarrow&\sin 2\alpha=2\sin\alpha\cos\alpha\end{array}$

Ainsi,

$\boxed{\sin 2\alpha=2\sin\alpha\cos\alpha}$

3) Calculons

$AH\$ et

$\ CH.$

$-\$ Calcul de

$AH$

En utilisant le cosinus de l'angle

$\widehat{HAB}$ , on obtient :

$\begin{array}{rcl}\dfrac{AH}{AB}=\cos\widehat{HAB}&\Leftrightarrow&AH=AB\cos\widehat{HAB}\\\\&\Leftrightarrow&AH=a\cos 2\alpha\end{array}$

D'où,

$\boxed{AH=a\cos 2\alpha}$

$-\$ Calcul de

$CH$

Utilisons le cosinus de l'angle

$\widehat{HCB}.$

On obtient alors :

$\begin{array}{rcl}\dfrac{CH}{BC}=\cos\widehat{HCB}&\Leftrightarrow&CH=BC\cos\widehat{HCB}\\\\&\Leftrightarrow&CH=2a\sin\alpha\cos\left(\dfrac{\pi}{2}-\alpha\right)\\\\&\Leftrightarrow&CH=2a\sin\alpha\sin\alpha\\\\&\Leftrightarrow&CH=2a\sin^{2}\alpha\end{array}$

Donc,

$\boxed{CH=2a\sin^{2}\alpha}$

En déduire la relation :

$cos 2\alpha=1-2\sin^{2}\alpha$

On sait que :

$AH+CH=AC$

Ce qui entraine :

$\begin{array}{rcl}a\cos 2\alpha+2a\sin^{2}\alpha=a&\Leftrightarrow&a\left(\cos 2\alpha+2\sin^{2}\alpha\right)=a\\\\&\Leftrightarrow&\cos 2\alpha+2\sin^{2}\alpha=1\\\\&\Leftrightarrow&\cos 2\alpha=1-2\sin^{2}\alpha\end{array}$

Par conséquent,

$\boxed{\cos 2\alpha=1-2\sin^{2}\alpha}$

Exercice 24

Exprimons à l'aide de

$\tan t$ les expressions suivantes :

Soit :

$X=\dfrac{\sin^{3}t-\cos^{3}t}{\sin t-\cos t}$

Alors, d'après la forme factorisée des identités remarquables, on a :

$\sin^{3}t-\cos^{3}t=(\sin t-\cos t)\left(\sin^{2}t+\sin t\cos t+\cos^{2}t\right)$

Ainsi, on obtient :

$\begin{array}{rcl}X&=&\dfrac{\sin^{3}t-\cos^{3}t}{\sin t-\cos t}\\\\&=&\dfrac{(\sin t-\cos t)\left(\sin^{2}t+\sin t\cos t+\cos^{2}t\right)}{\sin t-\cos t}\\\\&=&\sin^{2}t+\sin t\cos t+\cos^{2}t\\\\&=&\underbrace{\sin^{2}t+\cos^{2}t}_{=1}+\sin t\cos t\\\\&=&1+\sin t\cos t\end{array}$

Par ailleurs, en factorisant l'expression

$\sin t\cos t$ par

$\cos^{2}t$ , on obtient :

$\sin t\cos t=\cos^{2}t\times\dfrac{\sin t}{\cos t}$

Par suite,

$\begin{array}{rcl}X&=&1+\sin t\cos t\\\\&=&1+\cos^{2}t\times\dfrac{\sin t}{\cos t}\end{array}$

Or, on sait que :

$\cos^{2}t=\dfrac{1}{1+\tan^{2}t}$

Par conséquent,

$\begin{array}{rcl}X&=&1+\cos^{2}t\times\dfrac{\sin t}{\cos t}\\\\&=&1+\dfrac{1}{1+\tan^{2}t}\times\tan t\\\\&=&1+\dfrac{\tan t}{1+\tan^{2}t}\end{array}$

D'où,

$\boxed{X=1+\dfrac{\tan t}{1+\tan^{2}t}}$

Soit :

$Y=\cos^{2}t-\sin t\cos t$

Alors, en factorisant par

$\cos^{2}t$ , on obtient :

$\begin{array}{rcl}Y&=&\cos^{2}t-\sin t\cos t\\\\&=&\cos^{2}t\times\left(1-\dfrac{\sin t}{\cos t}\right)\end{array}$

Or, on sait que :

$\cos^{2}t=\dfrac{1}{1+\tan^{2}t}$

Donc, en remplaçant, on trouve :

$\begin{array}{rcl}Y&=&\cos^{2}t\times\left(1-\dfrac{\sin t}{\cos t}\right)\\\\&=&\dfrac{1}{1+\tan^{2}t}\times\left(1-\tan t\right)\\\\&=&\dfrac{1-\tan t}{1+\tan^{2}t}\end{array}$

Ainsi,

$\boxed{Y=\dfrac{1-\tan t}{1+\tan^{2}t}}$

Soit :

$Z=\dfrac{\sin^{2}t+\sin t\cos t}{\sin^{2}t-\cos^{2}t}$

Alors, en factorisant le numérateur et le dénominateur par

$\cos^{2}t$ , on obtient :

$\begin{array}{rcl}Z&=&\dfrac{\sin^{2}t+\sin t\cos t}{\sin^{2}t-\cos^{2}t}\\\\&=&\dfrac{\cos^{2}\left(\dfrac{\sin^{2}t}{\cos^{2}t}+\dfrac{\sin t}{\cos t}\right)}{\cos^{2}t\left(\dfrac{\sin^{2}t}{\cos^{2}t}-1\right)}\\\\&=&\dfrac{\dfrac{\sin^{2}t}{\cos^{2}t}+\dfrac{\sin t}{\cos t}}{\dfrac{\sin^{2}t}{\cos^{2}t}-1}\\\\&=&\dfrac{\tan^{2}t+\tan t}{\tan^{2}t-1}\\\\&=&\dfrac{\tan t(\tan t+1)}{(\tan t-1)(\tan t+1)}\\\\&=&\dfrac{\tan t}{\tan t-1}\end{array}$

D'où,

$\boxed{Z=\dfrac{\tan t}{\tan t-1}}$

Auteur:

Diny Faye