Solution des exercices : Applications linéaires - 4e
Classe:
Quatrième
Exercice 1
Complétons le tableau suivant pour que les suites de nombres $S_{1}\ $ et $\ S_{2}$ soient proportionnelles.
On utilisera le coefficient de proportionnalité permettant de passer de $S_{1}\ $ à $\ S_{2}.$
Ainsi, pour le passage des valeurs de la ligne $S_{1}$ à celles de la ligne $S_{2}$, on multipliera par ce même coefficient de proportionnalité.
On constate alors, pour passer de $4.8\ $ à $\ 14.4$, on multiplie $4.8$ par $3.$
C'est-à-dire, $14.4=3\times 4.8$
Par suite, le coefficient de proportionnalité permettant de passer de $S_{1}\ $ à $\ S_{2}$ est $3.$
Réciproquement, pour passer de $S_{2}\ $ à $\ S_{1}$, on multiplie par $\dfrac{1}{3}$, c'est-à-dire ; diviser par $3.$
On obtient alors, le tableau suivant :
$$\begin{array}{|c|c|c|c|c|c|c|}\hline S_{1}&2.4&3&3.6&4.8&6.2&11.3\\\hline S_{2}&7.2&9&10.8&14.4&18.6&33.9\\\hline\end{array}$$
Exercice 2
Un gèrent de télé centre propose à ses clients le tarif suivant : "Chaque minute de communication $60\;F$".
1) Exprimons la somme $y$ à payer en fonction du nombre $x$ de minutes de communication.
Soient $x$ le nombre de minutes de communication et $y$ la somme totale à payer.
On sait que pour chaque minute de communication, on paye $60\;F.$
Donc, pour $x$ minutes de communication, on payera $x\times 60\;F.$
Ainsi, la somme totale à payer, pour $x$ minutes de communication est donnée par : $y=x\times 60$
Par suite, $\boxed{y=60x}$
2) a) Calculons la somme à payer pour un client qui a fait $7$ minutes de communication.
Comme le client a fait $7$ minutes de communication, alors pour calculer somme à payer on remplace $x$ par $7$ dans l'équation précédente.
Ainsi, pour $x=7$, on a : $y=60\times 7=420$
D'où, $\boxed{y=420}$
Donc, pour un client qui a fait $7$ minutes de communication, la somme à payer est de $420\;F.$
b) Un client dispose $4\,800\;F.$ Calculons le nombre de minutes qu'il peut faire.
Dans l'équation précédente, $y$ représente la somme à payer. Donc, pour trouver le nombre de minutes à faire lorsqu'un client dispose d'une somme de $4\,800\;F$, on remplace $y$ par $4\,800\;F$ et essaie de trouver $x.$
Ainsi, pour $y=4\,800$, on a : $4\,800=60x$
Par suite, le nombre de minutes que ce client peut faire sera donné par : $x=\dfrac{4\,800}{60}=80$
D'où, $\boxed{x=80}$
Donc, un client qui dispose $4\,800\;F$ peut faire $80$ minutes de communication.
Exercice 3
Une bibliothèque de prêt demande à ses clients $300\;F$ par livre emprunté. On note $x$ le nombre de livres empruntés par un client en une année et $S(x)$ la somme à payer.
1) a) Exprimons $S(x)$ en fonction de $x.$
Soit $x$ le nombre de livres emprunté par un client en une année et soit $S(x)$ la somme totale payée pour ces $x$ livres empruntés.
On sait que pour chaque livre emprunté, on paye $300\;F.$
Donc, pour $x$ livres empruntés le client doit payer une somme égale à $300\times x\;F.$
Ainsi, si $S(x)$ est la somme totale payée pour ces $x$ livres empruntés alors, on aura : $S(x)=300\times x\;F$
Par suite, $\boxed{S(x)=300x}$
b) Donnons la nature de cette application.
On constate que $S(x)=300x$ est de la forme $S(x)=ax$ avec $a=300.$
Ce qui est caractéristique d'une application linéaire.
Donc, $S(x)$ est une application linéaire.
c) Déterminons son sens de variation.
Soit $S(x)=300x$, le coefficient de l'application linéaire $S$ est donc $300.$
Or, $300>0$ donc, $S$ est croissante
2) Représentons graphiquement $S$ avec comme échelle :
$-\ $ en abscisse : $1\;cm\ \longrightarrow\ 1\text{ livre}$
$-\ $ en ordonnée : $1\;cm\ \longrightarrow\ 300\;F$
Comme $S$ est une application linéaire alors, sa représentation graphique est une droite qui passe par $O$ origine du repère et par le point $A\begin{pmatrix} 1\\a\end{pmatrix}$ avec $a$ le coefficient de l'application linéaire.
Donc, cette droite passe par $O$ et par le point $A\begin{pmatrix} 1\\300\end{pmatrix}$
Par ailleurs, en tenant compte de l'échelle, on obtiendra une droite qui passe par $O$ et par le point $A\begin{pmatrix} 1\\1\end{pmatrix}$
Ainsi, on place donc le point $A$ dans le repère et ensuite, on trace la droite passant par $O$ et par $A.$
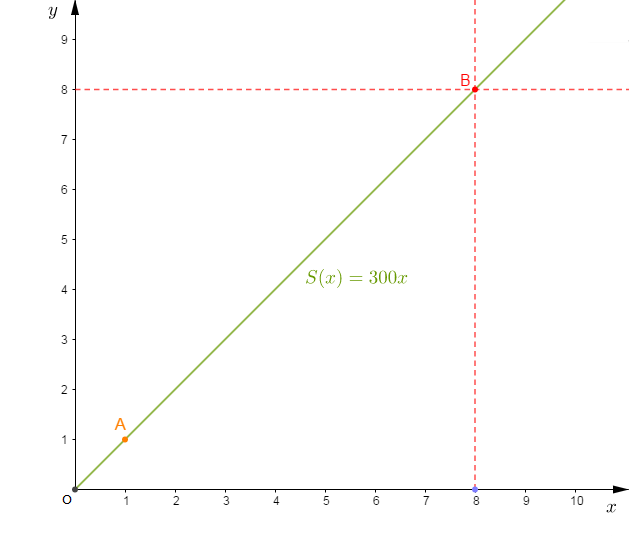
3) Déterminons graphiquement le nombre de livre emprunté par un client qui paie $2\,400\;F.$
D'après l'échelle, on a : $300\;F\ \longrightarrow\ 1\;cm$
Donc, $2\,400\;F\ \longrightarrow\ \dfrac{2\,400}{300}\times 1\;cm=8\;cm$
Ainsi, à partir de la valeur $8$ en ordonnée, on trace une droite horizontale. Soit $B$ le point de contact de cette droite avec la droite représentative de $S.$ A partir du point $B$, on trace une autre droite verticale qui coupe l'axe des abscisses en un point.
L'abscisse de ce point correspond au nombre de livres emprunté par un client qui paie $2\,400\;F$, en tenant compte de l'échelle.
On obtient alors la valeur $8\;cm.$ Or, d'après l'échelle, $1\;cm\ \longrightarrow\ 1\text{ livre}$
Donc, $8\;cm\ \longrightarrow\ 8\text{ livres}$
Par conséquent, un client qui paie $2\,400\;F$ peut emprunter $8$ livres.
Exercice 4
On considère les trois tableaux ci-dessous.
$$1\;.\ \begin{array}{|c|c|c|c|}\hline x&7&14&35 \\ \hline y&1&2&4 \\ \hline\end{array}\quad 2\;.\ \begin{array}{|c|c|c|c|}\hline x&1.5&2&2.5 \\ \hline y&4.5&6&7.5 \\ \hline\end{array}\quad 3\;.\ \begin{array}{|c|c|c|c|}\hline x&30&36&39 \\ \hline y&10&12&13 \\ \hline\end{array}$$
1) Véfifions si ces tableaux sont des tableaux de proportionnalité.
$-\ $ Pour le tableau $1$, on a :
$\dfrac{1}{7}=0.142$
$\dfrac{2}{14}=0.142$
$\dfrac{4}{35}=0.114$
Comme, $0.114$ est différent de $0.142$ alors, cette situation n'est pas proportionnelle à $x.$
Par conséquent, le tableau $1$ n'est pas un tableau proportionnalité.
$-\ $ Pour le tableau $2$, on a :
$\dfrac{4.5}{1.5}=3$ donc, $4.5=3\times 1.5$
$\dfrac{6}{2}=3$ donc, $6=3\times 2$
$\dfrac{7.5}{2.5}=3$ donc, $7.5=3\times 2.5$
Ainsi, pour le passage des valeurs de la première ligne à celles de la deuxième ligne, on multiplie par le même nombre $3.$
Par suite, le tableau $2$ représente une situation de proportionnalité.
$-\ $ Pour le tableau $3$, on a :
$\dfrac{10}{30}=\dfrac{1}{3}$ donc, $10=\dfrac{1}{3}\times 30$
$\dfrac{12}{36}=\dfrac{1}{3}$ donc, $12=\dfrac{1}{3}\times 36$
$\dfrac{13}{39}=\dfrac{1}{3}$ donc, $13=\dfrac{1}{3}\times 39$
Ainsi, pour le passage des valeurs de la première ligne à celles de la deuxième ligne, on multiplie par le même nombre $\dfrac{1}{3}.$
Ce qui signifie que le tableau $3$ représente un tableau de proportionnalité.
2) Déterminons l'application linéaire qui correspond aux tableaux $2\ $ et $\ 3$ sous la forme $y=ax$
Pour le tableau $2$, on sait que pour obtenir les valeurs de la ligne $y$, on multiplie celles de la ligne $x$ par un même coefficient $3.$
Donc, pour chaque valeur de $x$ donnée, la valeur de $y$ correspondante est obtenue en multipliant par $3$ la valeur de $x.$
Ce qui se traduit par : $y=3\times x$
Ainsi, l'application linéaire qui correspond au tableaux $2$ est :
$$y=3x$$
De la même manière, dans le tableau $3$, pour obtenir les valeurs de la ligne $y$, on multiplie celles de la ligne $x$ par un même coefficient $\dfrac{1}{3}.$
Donc, en multipliant chaque valeur de $x$ par le même coefficient $\dfrac{1}{3}$, on obtient la valeur de $y$ correspondante.
Ce qui signifie alors : $y=\dfrac{1}{3}\times x$
D'où, l'application linéaire qui correspond au tableaux $3$ est :
$$y=\dfrac{1}{3}x$$
Exercice 5
Parmi ces relations, identifions celles qui traduisent une application linéaire puis déterminons le coefficient de linéarité et le sens de variation.
En effet, toute relation entre $x\ $ et $\ y$ de la forme $y=ax$ avec $a$ un nombre rationnel, traduit une application linéaire.
Donc, pour les relations suivantes, il suffit de vérifier si elles peuvent se mettre sous cette forme.
1) a) Soit : $y=3x$ alors, on a une application linéaire, de coefficient de linéarité $3.$
Comme $3>0$ alors, cette application linéaire est croissante.
b) Soit : $y=3x-1$
On constate que cette relation ne peut pas se mettre sous la forme $y=ax$ donc, elle ne traduit pas une application linéaire.
c) Soit : $y=3$
On remarque que cette relation n'est pas de la forme $y=ax$ donc, elle n'est pas une application linéaire.
d) Soit $y =-3x$ alors, on a une application linéaire, de coefficient de linéarité $-3.$
$-3$ étant négatif alors, l'application linéaire est décroissante.
e) Soit $y=5x^{2}$
Comme la relation n'est pas de la forme $y=ax$ alors, elle ne traduit pas une application linéaire.
f) Soit $y=-x=(-1)\times x$, alors on a une application linéaire, de coefficient de linéarité $-1.$
Comme $-1$ est négatif alors, l'application linéaire est décroissante.
g) Soit $y=x=1\times x.$
Donc, cette relation traduit une application linéaire, de coefficient de linéarité $1.$
Or, $1$ est positif donc, l'application linéaire est croissante.
h) Soit $y=5x$ alors, on a une application linéaire, de coefficient de linéarité $5.$
$5$ étant positif donc, l'application linéaire est croissante.
2) a) Soit $y=-\dfrac{4}{3}x$
Cette relation traduit une application linéaire, de coefficient de linéarité $-\dfrac{4}{3}.$
Comme $-\dfrac{4}{3}<0$ alors, l'application linéaire est décroissante.
b) Soit : $y=3+\dfrac{5}{4}x$
On constate que cette relation ne peut pas se mettre sous la forme $y=ax.$
Par conséquent, elle ne traduit pas une application linéaire.
c) Soit : $y=\dfrac{3x+1}{2}-\dfrac{1}{2}$ alors, on a :
$\begin{array}{rcl} y&=&\dfrac{3x+1}{2}-\dfrac{1}{2}\\\\&=&\dfrac{3x+1-1}{2}\\\\&=&\dfrac{3x+0}{2}\\\\&=&\dfrac{3}{2}x\end{array}$
Donc, on obtient finalement : $y=\dfrac{3}{2}x$ qui traduit bien une application linéaire, de coefficient de linéarité $\dfrac{3}{2}$
Comme $\dfrac{3}{2}>0$ alors, l'application linéaire est croissante.
Exercice 6 "Image et antécédent"
On considère l'application : $y=-2x.$
1) a) Cette application est linéaire.
Justifions.
On a : la relation $y=-2x$ signifie que pour tout nombre rationnel $x$, on associe le nombre rationnel $y$ égal à $-2\times x.$
Donc, l'application $y=-2x$ est une application linéaire.
b) Le nombre $-2$ s'appelle le coefficient de linéarité de l'application.
c) $y$ représente l'image de $x$ par cette application linéaire
$x$ représente l'antécédent de $y$ par cette même application linéaire.
2) Calculons les images de : $2\;;\ -3\;;\ 0\ $ et $\ 3\pi.$
$-\ $ image de $2$
Dans la relation $y=-2x$, on remplace $x$ par $2$ et on trouve la valeur de $y.$
On a alors :
$\begin{array}{rcl} y&=&-2x\\\\&=&-2\times 2\\\\&=&-4\end{array}$
Donc, l'image de $2$ par cette application linéaire est égale à $-4.$
$-\ $ image de $-3$
Dans la relation $y=-2x$, en remplaçant $x$ par $-3$ et on obtient la valeur de $y.$
On a alors :
$\begin{array}{rcl} y&=&-2x\\\\&=&-2\times (-3)\\\\&=&6\end{array}$
Donc, l'image de $-3$ par cette application linéaire est égale à $6.$
$-\ $ image de $0$
Dans la relation $y=-2x$, en remplaçant $x$ par $0$ et on trouve $y=0.$
Ce qui signifie que $0$ est l'image de $0$ par cette application linéaire.
$-\ $ image de $3\pi$
Dans la relation $y=-2x$, en remplaçant $x$ par $3\pi$ on obtient la valeur de $y.$
On a alors :
$\begin{array}{rcl} y&=&-2x\\\\&=&-2\times 3\pi\\\\&=&-6\pi\end{array}$
Donc, l'image de $3\pi$ par cette application linéaire est égale à $-6\pi.$
3) Calculons les antécédents des nombres : $-4\;;\ \dfrac{4}{3}\ $ et $\ 2\pi.$
$-\ $ antécédent de $-4$
D'après le résultat de la question $2)$, on a : $-4$ est l'image de $2$ par cette application linéaire.
Ce qui signifie que $2$ est l'antécédent de $-4$ par cette même application linéaire.
$-\ $ antécédent de $\dfrac{4}{3}$
Dans la relation $y=-2x$, en remplaçant $y$ par $\dfrac{4}{3}$ on obtient : $\dfrac{4}{3}=-2x$
On résout alors l'équation $-2x=\dfrac{4}{3}$ pour trouver la valeur de $x.$
On a :
$\begin{array}{rcl} -2x=\dfrac{4}{3}&\Leftrightarrow&x=\dfrac{\dfrac{4}{3}}{-2}\\\\&\Leftrightarrow&x=\dfrac{4\times 1}{3\times(-2)}\\\\&\Leftrightarrow&x=\dfrac{4}{-6}\\\\&\Leftrightarrow&x=\dfrac{2}{-3}\end{array}$
Donc, $\dfrac{2}{-3}$ est l'antécédent de $\dfrac{4}{3}$ par cette application linéaire.
$-\ $ antécédent de $2\pi$
Dans la relation $y=-2x$, on remplace $y$ par $2\pi.$ Ce qui donne : $2\pi=-2x$
On résout alors l'équation $-2x=2\pi$ pour trouver la valeur de $x.$
On a :
$\begin{array}{rcl} -2x=2\pi&\Leftrightarrow&x=\dfrac{2\pi}{-2}\\\\&\Leftrightarrow&x=-\pi\end{array}$
Donc, $-\pi$ est l'antécédent de $2\pi$ par cette application linéaire.
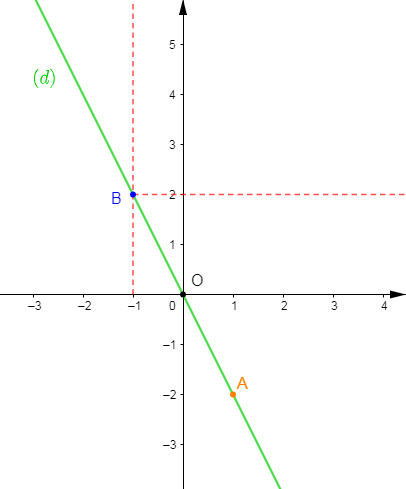
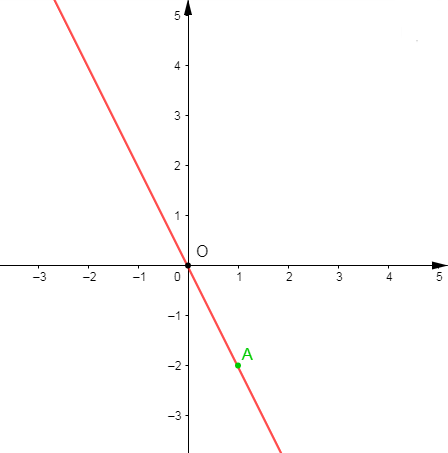
4) a) Traçons $(d)$ la représentation graphique de cette application dans un repère orthonormé.
On sait que : la représentation graphique d'une application linéaire est une droite qui passe par $O$ ; origine du repère et par le point $A\begin{pmatrix} 1\\a\end{pmatrix}$ avec $a$ le coefficient de l'application linéaire.
on a : le coefficient de linéarité $a$ de cette application est égal à $-2.$
Donc, $(d)$ est la droite qui passe par $O$ et par $A\begin{pmatrix} 1\\-2\end{pmatrix}.$
On place alors le point $A$ dans dans un repère orthonormé puis, on trace la droite $(d)$ passant par $O$ et par le point $A.$

b) Déterminons graphiquement l'image de $-1.$
Pour cela, on se place sur l'axe des abscisses à la valeur $-1$ puis, on trace une droite verticale.
Cette droite coupe la droite $(d)$ au point $B.$
Alors, à partir de ce point $B$, on trace une droite horizontale.
On constate que cette droite coupe l'axe des ordonnées à la valeur $2.$
Par conséquent, $2$ est l'image de $-1$ par cette application linéaire.
Exercice 7 "Détermination d'une application linéaire"
$f$ est une application linéaire, on sait que : $f(2)=-4.$
1) Trouvons le coefficient $a$ de cette application linéaire.
Comme $f$ est une application linéaire alors, pour tout nombre rationnel $x$, on a :
$$f(x)=ax$$
avec $a$ le coefficient de linéarité.
On sait que $f(2)=-4$
Donc, dans l'expression $f(x)=ax$, en remplaçant $x$ par $2$, on obtient :
$\begin{array}{rcl} f(2)=-4&\Leftrightarrow&a\times 2=-4\\\\&\Leftrightarrow&a=\dfrac{-4}{2}\\\\&\Leftrightarrow&a=-2\end{array}$
Donc, $\boxed{a=-2}$
2) Donnons l'expression de $x$ par $f$ puis la représentation graphique de cette application dans un repère orthonormé.
Dans l'expression $f(x)=ax$, on remplace $a$ par $-2.$
On obtient alors :
$$f(x)=-2x$$
Comme $f(x)$ est une application linéaire alors, sa représentation graphique est une droite qui passe par $O$ ; origine du repère et par le point $A\begin{pmatrix} 1\\a\end{pmatrix}$ avec $a$ le coefficient de l'application linéaire.
on a : $a=-2.$
Donc, on trace la droite qui passe par $O$ et par $A\begin{pmatrix} 1\\-2\end{pmatrix}.$

3) Calculons de deux façons l'image de $2\,008.$
$1e\;$ façon : on utilise le calcul direct
On calcule $f(2\,008).$ Pour cela, on remplace $x$ par $2\,008$, dans l'expression de $f(x)=-2x.$
On a alors :
$\begin{array}{rcl} f(2\,008)&=&-2\times 2\,008\\\\&=&-4\,016\end{array}$
Donc, l'image de $2\,008$ par l'application linéaire $f$ est égale à $-4\,016.$
$2e\;$ façon : on utilise la propriété de la linéarité
On peut écrire : $2\,008=2\,000+8$
Donc, on a : $f(2\,008)=f(2\,000+8)$
D'après une propriété de la linéarité, on a :
$$f(2\,000+8)=f(2\,000)+f(8)$$
Ainsi,
$\begin{array}{rcl} f(2\,008)&=&f(2\,000+8)\\\\&=&f(2\,000)+f(8)\\\\&=&-2\times 2\,000+(-2)\times 8\\\\&=&-4\,000-16\\\\&=&-4\,016\end{array}$
Donc, $-4\,016$ est l'image de $2\,008$ par l'application linéaire $f.$
Exercice 8 "Propriété de la linéarité"
Calculons le coefficient des applications linéaires $f\;,\ g\ $ et $\ h.$
1) $f$ est telle que : $f(2)+f(-3)=6$
Soit $f(x)=ax.$
Comme $f$ est une application linéaire alors, d'après une propriété de la linéarité, on a :
$$f(2)+f(-3)=f(2-3)=f(-1)$$
Ainsi,
$\begin{array}{rcl} f(2)+f(-3)=6&\Leftrightarrow&f(2-3)=6\\\\&\Leftrightarrow&f(-1)=6\\\\&\Leftrightarrow&a\times(-1)=6\\\\&\Leftrightarrow&a=\dfrac{6}{-1}\\\\&\Leftrightarrow&a=-6\end{array}$
Donc, $\boxed{a=-6}$
2) $g$ est telle que : $3g(2)=1.5$
Soit $g(x)=ax$
Comme $g$ est une application linéaire alors, d'après une propriété de la linéarité, on a :
$$3g(2)=g(3\times 2)=g(6)$$
Donc,
$\begin{array}{rcl} 3g(2)=1.5&\Leftrightarrow&g(3\times 2)=1.5\\\\&\Leftrightarrow&g(6)=1.5\\\\&\Leftrightarrow&a\times 6=1.5\\\\&\Leftrightarrow&a=\dfrac{1.5}{6}\\\\&\Leftrightarrow&a=0.25\end{array}$
Ainsi, $\boxed{a=0.25}$
3) $h$ est telle que : $h(-2)-\dfrac{1}{2}h(3)=2$
Soit $h(x)=ax$
Comme $h$ est une application linéaire alors, d'après une propriété de la linéarité, on a :
$$\dfrac{1}{2}h(3)=h\left(\dfrac{1}{2}\times 3\right)=h\left(\dfrac{3}{2}\right)$$
Donc, en remplaçant $\dfrac{1}{2}h(3)$ par $h\left(\dfrac{3}{2}\right)$, on obtient :
$$h(-2)-\dfrac{1}{2}h(3)=h(-2)-h\left(\dfrac{3}{2}\right)$$
En appliquant encore une propriété de la linéarité, on trouve :
$$h(-2)-h\left(\dfrac{3}{2}\right)=h\left(-2-\dfrac{3}{2}\right)=h\left(-\dfrac{4}{2}-\dfrac{3}{2}\right)=h\left(-\dfrac{7}{2}\right)$$
Ainsi, on a :
$\begin{array}{rcl} h(-2)-\dfrac{1}{2}h(3)=2&\Leftrightarrow&h(-2)-h\left(\dfrac{3}{2}\right)=2\\\\&\Leftrightarrow&h\left(-\dfrac{7}{2}\right)=2\\\\&\Leftrightarrow&a\times\left(-\dfrac{7}{2}\right)=2\\\\&\Leftrightarrow&a=\dfrac{2}{-\dfrac{7}{2}}\\\\&\Leftrightarrow&a=-\dfrac{2\times 2}{7}\\\\&\Leftrightarrow&a=-\dfrac{4}{7}\end{array}$
D'où, $\boxed{a=-\dfrac{4}{7}}$
Exercice 9 "Détermination d'une application linéaire"
1) Déterminons l'application linéaire $g$ définie par : $$3g(2)+g(1)=-14$$
Comme $g$ est une application linéaire alors, pour tout nombre rationnel $x$, on a :
$$g(x)=ax$$
Déterminons alors son coefficient de linéarité $a.$
On sait que : $3g(2)+g(1)=-14$
Or, d'après une propriété de la linéarité, on a :
$$3g(2)=h(3\times 2)=g(6)$$
Donc :
$$3g(2)+g(1)=g(6)+g(1)$$
En appliquant encore une propriété de la linéarité, on obtient :
$$g(6)+g(1)=g(6+1)=g(7)$$
Ainsi, on a :
$\begin{array}{rcl} 3g(2)+g(1)=-14&\Leftrightarrow&g(6)+g(1)=-14\\\\&\Leftrightarrow&g(7)=-14\\\\&\Leftrightarrow&a\times 7=-14\\\\&\Leftrightarrow&a=\dfrac{-14}{7}\\\\&\Leftrightarrow&a=-2\end{array}$
D'où, $\boxed{a=-2}$
Par conséquent, l'application linéaire $g$ est définie par :
$$g(x)=-2x$$
2) Déterminons le sens de variation de $g$ puis calculons $g\left(-\dfrac{1}{3}\right)$
Comme le coefficient de linéarité $-2$ est inférieur à $0$ alors, l'application linéaire $g$ est décroissante.
$-\ $ Calcul de $g\left(-\dfrac{1}{3}\right)$
On a :
$\begin{array}{rcl} g\left(-\dfrac{1}{3}\right)&=&-2\times \left(-\dfrac{1}{3}\right)\\\\&=&\dfrac{2}{3}\end{array}$
Donc, $\boxed{g\left(-\dfrac{1}{3}\right)=\dfrac{2}{3}}$
3) Représentons $g$ dans un repère orthonormé.
Comme $g$ est une application linéaire alors, sa représentation graphique est une droite qui passe par $O$ ; origine du repère et par le point $A\begin{pmatrix} 1\\a\end{pmatrix}$ avec $a$ le coefficient de l'application linéaire.
on a : $a=-2.$
Donc, on trace la droite passant par $O$ et par $A\begin{pmatrix} 1\\-2\end{pmatrix}.$

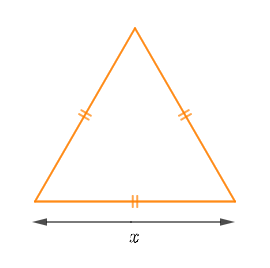
Exercice 10 "Triangle équilatéral et application linéaire"
On désigne $x$ le côté d'un triangle équilatéral et $p(x)$ le périmètre du triangle.

1) Exprimons $p(x)$ en fonction de $x$ puis donnons la nature de cette application.
On sait que : dans un triangle équilatéral, les côtés ont même longueur.
Alors, on a :
$$\text{Périmètre du triangle équilatéral}=3\times\text{Longueur d'un côté}$$
Donc, si $x$ est la longueur d'un côté alors, le périmètre $p(x)$ de ce triangle équilatéral est donné par :
$\begin{array}{rcl} p(x)&=&3\times\text{Longueur d'un côté}\\\\&=&3\times x\\\\&=&3x\end{array}$
D'où, $\boxed{p(x)=3x}$
L'application $p(x)=3x$ est donc une application linéaire de coefficient de linéarité $3.$
2) Calculons $x$ si le périmètre est de $27\;m.$
Le périmètre est égal à $27\,m$ signifie que $p(x)=27\,m.$
Comme $p(x)=3x$ alors, pour trouver la valeur de $x$, on va résoudre l'équation : $3x=27$
On a :
$\begin{array}{rcl} 3x=27&\Leftrightarrow&x=\dfrac{27}{3}\\\\&\Leftrightarrow&x=9\end{array}$
D'où, $\boxed{x=9\,m}$
Exercice 11 "Le rectangle et application linéaire"
Soit $x$ la longueur d'un rectangle de largeur $6\;m.$
1) Exprimons le périmètre $p(x)$ en fonction de $x.$
On sait que le périmètre d'un rectangle de longueur $L$ et de largeur $\ell$ est donné par :
$$\text{Périmètre du rectangle}=2\times(L+\ell)$$
Donc, si la longueur $L$ est égale à $x$ et la largeur $\ell$ égale à $6\;m$ alors, le périmètre $p(x)$ de ce rectangle est donné par :
$\begin{array}{rcl} p(x)&=&2\times(L+\ell)\\\\&=&2\times(x+6)\\\\&=&2\times x+2\times 6\\\\&=&2x+12\end{array}$
D'où, $\boxed{p(x)=2x+12}$
2) Exprimons l'aire $\mathcal{A}(x)$ en fonction de $x.$
On sait que l'aire $\mathcal{A}(x)$ de ce rectangle est donnée par :
$$\mathcal{A}(x)=\ell\times L$$
On remplace $L$ par sa valeur $x$ et $\ell$ par sa valeur $6.$
On obtient alors :
$\begin{array}{rcl} \mathcal{A}(x)&=&\ell\times L\\\\&=&6\times x\\\\&=&6x\end{array}$
D'où, $\boxed{\mathcal{A}(x)=6x}$
3) Calculons $x$ si le périmètre est de $38\;m.$
D'après le résultat de la question $1)$, on a : $p(x)=2x+12.$
Comme le périmètre est égal à $38\,m$ alors, cela signifie que $p(x)=38\,m.$
Donc, pour trouver la valeur de $x$, on va résoudre l'équation : $2x+12=38$
On a :
$\begin{array}{rcl} 2x+12=38&\Leftrightarrow&2x=38-12\\\\&\Leftrightarrow&2x=26\\\\&\Leftrightarrow&x=\dfrac{26}{2}\\\\&\Leftrightarrow&x=13\end{array}$
D'où, $\boxed{x=13\,m}$
4) Calculons l'aire $\mathcal{A}$ si la longueur est égale à $6.5\;m$
D'après le résultat de la question $2)$, on a l'aire $\mathcal{A}(x)=6x$ avec $x$ la longueur de ce rectangle.
Donc, si cette longueur $x$ est égale à $6.5\;m$ alors, pour trouver l'aire $\mathcal{A}$, on remplace $x$ par $6.5$ dans l'expression de $\mathcal{A}(x).$
C'est-à-dire, on calcule $\mathcal{A}(6.5).$
On a alors :
$\begin{array}{rcl} \mathcal{A}(6.5)&=&6\times 6.5\\\\&=&39\end{array}$
D'où, $\boxed{\mathcal{A}=39\;m^{2}}$
Exercice 12 "Représentation graphique d'une application linéaire"
On considère les applications linéaires $f$ et $g$ telles que :
$$f(x)=-\dfrac{1}{2}x\quad\text{et}\quad g(x)=2x$$
1) Calculons les images par $f$ des nombres : $0\;;\ -3\ $ et $\ -\pi.$
$-\ $ image de $0$
On calcule $f(0)$ en remplaçant $x$ par $0$ dans la relation $f(x)=-\dfrac{1}{2}x.$
On a alors :
$\begin{array}{rcl} f(0)&=&-\dfrac{1}{2}\times 0\\\\&=&0\end{array}$
Donc, l'image de $0$ par $f$ est égale à $0.$
$-\ $ image de $-3$
On calcule $f(-3).$ Pour cela, on remplace $x$ par $-3$ dans la relation $f(x)=-\dfrac{1}{2}x.$
Alors, on a :
$\begin{array}{rcl} f(-3)&=&-\dfrac{1}{2}\times(-3)\\\\&=&\dfrac{3}{2}\end{array}$
Donc, $\dfrac{3}{2}$ est l'image de $-3$ par l'application linéaire $f.$
$-\ $ image de $-\pi$
On calcule $f(-\pi)$ en remplaçant $x$ par $-\pi$ dans la relation $f(x)=-\dfrac{1}{2}x.$
On a alors :
$\begin{array}{rcl} f(-\pi)&=&-\dfrac{1}{2}\times(-\pi)\\\\&=&\dfrac{\pi}{2}\end{array}$
D'où, l'image de $-\pi$ par $f$ est égale à $\dfrac{\pi}{2}.$
2) Calculons les images par $g$ des nombres : $2\;;\ 3\ $ et $\ -5\pi.$
$-\ $ image de $2$
On calcule alors $g(2)$ en remplaçant $x$ par $2$ dans la relation $g(x)=2x.$
Ce qui donne :
$\begin{array}{rcl} g(2)&=&2\times 2\\\\&=&4\end{array}$
Donc, l'image de $2$ par l'application linéaire $g$ est égale à $4.$
$-\ $ image de $3$
On calcule $g(3).$ Pour cela, on remplace $x$ par $3$ dans la relation $g(x)=2x.$
On a alors :
$\begin{array}{rcl} g(3)&=&2\times 3\\\\&=&6\end{array}$
D'où, $6$ est l'image de $3$ par l'application $g.$
$-\ $ image de $-5\pi$
On calcule $g(-5\pi)$ en remplaçant $x$ par $-5\pi$ dans la relation $g(x)=2x.$
Alors, on a :
$\begin{array}{rcl} g(-5\pi)&=&2\times(-5\pi)\\\\&=&-10\pi\end{array}$
Donc, l'image de $-5\pi$ par $g$ est égale à $-10\pi.$
3) Calculons les antécédents par $f$ des nombres $4\ $ et $\ -6.$
$-\ $ antécédent de $4$
Dans la relation $f(x)=-\dfrac{1}{2}x$, en remplaçant $f(x)$ par $4$ on obtient : $4=-\dfrac{1}{2}x$
On résout alors l'équation $-\dfrac{1}{2}x=4$ pour trouver la valeur de $x.$
On a :
$\begin{array}{rcl} -\dfrac{1}{2}x=4&\Leftrightarrow&-x=4\times 2\\\\&\Leftrightarrow&-x=8\\\\&\Leftrightarrow&x=\dfrac{8}{-1}\\\\&\Leftrightarrow&x=-8\end{array}$
Donc, $-8$ est l'antécédent de $4$ par l'application linéaire $f.$
$-\ $ antécédent de $-6$
Dans la relation $f(x)=-\dfrac{1}{2}x$, on remplace $f(x)$ par $-6.$
Ce qui donne : $-6=-\dfrac{1}{2}x$
On résout alors l'équation $-\dfrac{1}{2}x=-6$ pour trouver la valeur de $x.$
On a :
$\begin{array}{rcl} -\dfrac{1}{2}x=-6&\Leftrightarrow&-x=-6\times 2\\\\&\Leftrightarrow&-x=-12\\\\&\Leftrightarrow&x=\dfrac{-12}{-1}\\\\&\Leftrightarrow&x=12\end{array}$
Ainsi, l'antécédent de $-6$ par $f$ est égal à $12.$
4) Calculons les antécédents par $g$ des nombres $4\ $ et $\ -6.$
$-\ $ antécédent de $4$
Dans la relation $g(x)=2x$, en remplaçant $g(x)$ par $4$ on obtient : $4=2x$
On résout alors l'équation $2x=4$ pour trouver la valeur de $x.$
On a :
$\begin{array}{rcl} 2x=4&\Leftrightarrow&x=\dfrac{4}{2}\\\\&\Leftrightarrow&x=2\end{array}$
Donc, $2$ est l'antécédent de $4$ par l'application linéaire $g.$
$-\ $ antécédent de $-6$
Dans la relation $g(x)=2x$, on remplace $g(x)$ par $-6.$
On obtient alors : $-6=2x$
Donc, en résolvant l'équation $2x=-6$, on trouve la valeur de $x.$
On a :
$\begin{array}{rcl} 2x=-6&\Leftrightarrow&x=\dfrac{-6}{2}\\\\&\Leftrightarrow&x=-3\end{array}$
D'où, l'antécédent de $-6$ par $g$ est égal à $-3.$
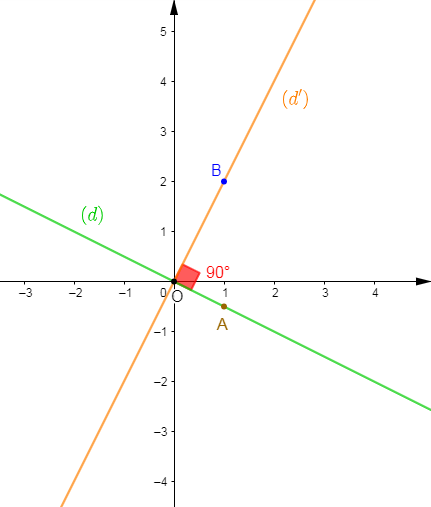
5) Traçons la droite $(d)$ représentation graphique de $f.$
On a : $f(x)=-\dfrac{1}{2}x$
Comme $f$ est une application linéaire de coefficient $-\dfrac{1}{2}$ alors, sa représentation graphique est une droite qui passe par $O$ ; origine du repère et par le point $A\begin{pmatrix} 1\\-\dfrac{1}{2}\end{pmatrix}.$
Donc, on place le point $A\begin{pmatrix} 1\\-\dfrac{1}{2}\end{pmatrix}$ et on trace la droite $(d)$ passant par $O\ $ et $\ A.$
6) Traçons la droite $(d')$ représentation graphique de $g.$
On a : $g(x)=2x$
Comme $g$ est une application linéaire de coefficient $2$ alors, sa représentation graphique est une droite qui passe par $O$ ; origine du repère et par le point $B\begin{pmatrix} 1\\2\end{pmatrix}.$
On place alors le point $B\begin{pmatrix} 1\\2\end{pmatrix}$ puis, on trace la droite $(d')$ passant par $O\ $ et $\ B.$
7) Vérifions que $(d)\ $ et $\ (d')$ sont perpendiculaires.
On remarque que les deux droites $(d)\ $ et $\ (d')$ sont sécantes en $O.$
En mesurant l'angle $\widehat{AOB}$ formé par ces deux droites, on trouve $90^{\circ}.$
Ce qui signifie que les droites $(d)\ $ et $\ (d')$ sont perpendiculaires.

Exercice 13
On donne les applications linéaires suivantes $m\;,\ k\ $ et $\ l$ telles que :
$$m(x)=\dfrac{x}{3}\;,\ k(x)=-\dfrac{1}{2}x\;,\ l(x)=7x$$
1) Indiquons le coefficient de linéarité de chaque application linéaire.
On a :
$m(x)=\dfrac{x}{3}=\dfrac{1}{3}x$ donc, le coefficient de linéarité de $m$ est égal à $\dfrac{1}{3}.$
$k(x)=-\dfrac{1}{2}x$, ce qui signifie que $\dfrac{1}{2}$ est le coefficient de linéarité de $k.$
$l(x)=7x=7$ donc, l'application $l$ a pour coefficient de linéarité $7.$
2) Calculons l'image de chacun des rationnels suivants : $-2\;;\ \dfrac{1}{3}\;;\ -\dfrac{3}{2}$ par les applications linéaires $m\;,\ k\ $ et $\ l.$
$-\ $ image de $-2$ par $m$
On calcule $m(-2)$ en remplaçant $x$ par $-2$ dans la relation $m(x)=\dfrac{x}{3}.$
Alors, on a : $m(-2)=\dfrac{-2}{3}$
Donc, l'image de $-2$ par $m$ est égale à $\dfrac{-2}{3}.$
$-\ $ image de $-2$ par $k$
On calcule $k(-2)$ en remplaçant $x$ par $-2$ dans la relation $k(x)=-\dfrac{1}{2}x.$
On a alors :
$\begin{array}{rcl} k(-2)&=&-\dfrac{1}{2}\times(-2)\\\\&=&\dfrac{2}{2}\\\\&=&1\end{array}$
D'où, l'image de $-2$ par $k$ est égale à $1.$
$-\ $ image de $-2$ par $l$
On calcule $l(-2)$ en remplaçant $x$ par $-2$ dans la relation $l(x)=7x.$
Alors, on a :
$\begin{array}{rcl} l(-2)&=&7\times(-2)\\\\&=&-14\end{array}$
Ainsi, $-14$ est l'image de $-2$ par $l.$
$-\ $ image de $\dfrac{1}{3}$ par $m$
On calcule $m\left(\dfrac{1}{3}\right)$ en remplaçant $x$ par $\dfrac{1}{3}$ dans la relation $m(x)=\dfrac{1}{3}x.$
Alors, on a :
$\begin{array}{rcl} m\left(\dfrac{1}{3}\right)&=&\dfrac{1}{3}\times\dfrac{1}{3}\\\\&=&\dfrac{1}{3\times 3}\\\\&=&\dfrac{1}{9}\end{array}$
D'où, l'image de $\dfrac{1}{3}$ par $m$ est égale à $\dfrac{1}{9}.$
$-\ $ image de $\dfrac{1}{3}$ par $k$
On calcule $k\left(\dfrac{1}{3}\right)$ en remplaçant $x$ par $\dfrac{1}{3}$ dans la relation $k(x)=-\dfrac{1}{2}x.$
On a alors :
$\begin{array}{rcl} k\left(\dfrac{1}{3}\right)&=&-\dfrac{1}{2}\times\dfrac{1}{3}\\\\&=&-\dfrac{1}{2\times 3}\\\\&=&-\dfrac{1}{6}\end{array}$
Donc, l'image de $\dfrac{1}{3}$ par $k$ est égale à $-\dfrac{1}{6}.$
$-\ $ image de $\dfrac{1}{3}$ par $l$
On calcule $l\left(\dfrac{1}{3}\right)$ en remplaçant $x$ par $\dfrac{1}{3}$ dans la relation $l(x)=7x.$
Alors, on a :
$\begin{array}{rcl} l\left(\dfrac{1}{3}\right)&=&7\times\dfrac{1}{3}\\\\&=&\dfrac{7}{3}\end{array}$
Ainsi, $\dfrac{7}{3}$ est l'image de $\dfrac{1}{3}$ par $l.$
$-\ $ image de $-\dfrac{3}{2}$ par $m$
On calcule $m\left(-\dfrac{3}{2}\right)$ en remplaçant $x$ par $-\dfrac{3}{2}$ dans la relation $m(x)=\dfrac{1}{3}x.$
Alors, on a :
$\begin{array}{rcl} m\left(-\dfrac{3}{2}\right)&=&\dfrac{1}{3}\times\left(-\dfrac{3}{2}\right)\\\\&=&-\dfrac{3}{3\times 2}\\\\&=&-\dfrac{1}{2}\end{array}$
D'où, l'image de $-\dfrac{3}{2}$ par $m$ est égale à $-\dfrac{1}{2}.$
$-\ $ image de $-\dfrac{3}{2}$ par $k$
On calcule $k\left(-\dfrac{3}{2}\right)$ en remplaçant $x$ par $-\dfrac{3}{2}$ dans la relation $k(x)=-\dfrac{1}{2}x.$
On a alors :
$\begin{array}{rcl} k\left(-\dfrac{3}{2}\right)&=&-\dfrac{1}{2}\times\left(-\dfrac{3}{2}\right)\\\\&=&\dfrac{1\times 3}{2\times 2}\\\\&=&\dfrac{3}{4}\end{array}$
Ainsi, $\dfrac{3}{4}$ est l'image de $-\dfrac{3}{2}$ par $k.$
$-\ $ image de $-\dfrac{3}{2}$ par $l$
On calcule $l\left(-\dfrac{3}{2}\right)$ en remplaçant $x$ par $-\dfrac{3}{2}$ dans la relation $l(x)=7x.$
Alors, on a :
$\begin{array}{rcl} l\left(-\dfrac{3}{2}\right)&=&7\times\left(-\dfrac{3}{2}\right)\\\\&=&-\dfrac{21}{2}\end{array}$
D'où, $-\dfrac{21}{2}$ est l'image de $-\dfrac{3}{2}$ par $l.$
Exercice 14
Soit l'application linéaire $g$ telle que $g(6)=18.$
$18$ est l'image de $6$ par $g$ et $6$ représente l'antécédent $18$ par $g.$
Exercice 15
Soit l'application $k$ définie par $k(x)=\dfrac{1}{2}x.$
Calculons l'antécédent de $\dfrac{3}{4}$ par $k.$
Dans la relation $k(x)=\dfrac{1}{2}x$, on remplace $k(x)$ par $\dfrac{3}{4}.$
On obtient alors : $\dfrac{3}{4}=\dfrac{1}{2}x.$
Donc, en résolvant l'équation $\dfrac{1}{2}x=\dfrac{3}{4}$, on trouve la valeur de $x.$
On a :
$\begin{array}{rcl}\dfrac{1}{2}x=\dfrac{3}{4}&\Leftrightarrow&x=\dfrac{\dfrac{3}{4}}{\dfrac{1}{2}}\\\\&\Leftrightarrow&x=\dfrac{3}{4}\times\dfrac{2}{1}\\\\&\Leftrightarrow&x=\dfrac{3\times 2}{4}\\\\&\Leftrightarrow&x=\dfrac{3}{2}\end{array}$
Ainsi, l'antécédent de $\dfrac{3}{4}$ par l'application linéaire $k$ est égal à $\dfrac{3}{2}.$
Exercice 16
Déterminons l'application linéaire $g$ pour laquelle $-18$ est l'image de $3.$
Comme $g$ est une application linéaire alors, pour tout nombre rationnel $x$, on a :
$$g(x)=a\times x$$
avec $a$ coefficient de linéarité.
Trouvons alors la valeur de $a.$
On sait que $-18$ est l'image de $3$ par $g.$
Ce qui peut encore s'écrire : $g(3)=-18.$
Alors, en remplaçant $x$ par $3$ dans la relation $g(x)=ax$, on obtient : $g(3)=a\times 3$
Donc, $a\times 3=-18$
Ce qui donne : $a=\dfrac{-18}{3}=-6$
D'où,
$$g(x)=-6x$$
Exercice 17
Soit $g(x)=\dfrac{1}{2}x.$
1) Déterminons l'image par $g$ de chacun des nombres suivants : $-4\;;\ 2\;;\ \dfrac{2}{5}.$
On a :
$\begin{array}{rcl} g(-4)&=&\dfrac{1}{2}\times(-4)\\\\&=&\dfrac{-4}{2}\\\\&=&-2\end{array}$
Donc, $-2$ est l'image de $-4$ par $g.$
On a :
$\begin{array}{rcl} g(2)&=&\dfrac{1}{2}\times 2\\\\&=&\dfrac{2}{2}\\\\&=&1\end{array}$
Donc, l'image de $2$ par $g$ est égale à $1.$
On a :
$\begin{array}{rcl} g\left(\dfrac{2}{5}\right)&=&\dfrac{1}{2}\times\dfrac{2}{5}\\\\&=&\dfrac{2}{2\times 5}\\\\&=&\dfrac{1}{5}\end{array}$
Donc, $\dfrac{1}{5}$ est l'image de $\dfrac{2}{5}$ par $g.$
2) Notons les résultats dans un tableau de correspondance.
$$\begin{array}{|c|c|c|c|}\hline x&-4&2&\dfrac{2}{5} \\ \hline g(x)&-2&1&\dfrac{1}{5} \\ \hline\end{array}$$
3) Justifions que c'est un tableau de proportionnalité.
D'après les résultats de la question $1)$, on constate que les valeurs de la deuxième ligne du tableau sont obtenues en multipliant celles de la première ligne par le même nombre $\dfrac{1}{2}.$
Par conséquent, ce tableau représente une situation de proportionnalité.
Exercice 18
Soit l'application linéaire $h$ telle que $h(-4)=8\;;\ h(7)=-14.$
Sans déterminer le coefficient de linéarité, calculons $h(3)\;;\ h(21)\;;\ h(-28)\ $ et $\ h(11).$
$-\ $ calcul de $h(3)$
On sait que : $-4+7=3$
Donc, on a : $h(3)=h(-4+7)$
Or, d'après une propriété de la linéarité, on a :
$$h(-4+7)=h(-4)+h(7)$$
On obtient alors :
$\begin{array}{rcl} h(3)&=&h(-4+7)\\\\&=&h(-4)+h(7)\\\\&=&8-14\\\\&=&-6\end{array}$
D'où, $\boxed{h(3)=-6}$
$-\ $ calcul de $h(21)$
On sait que : $21=3\times 7$
Donc, on peut écrire : $h(21)=h(3\times 7)$
En appliquant une propriété de la linéarité, on obtient :
$$h(3\times 7)=3\times h(7)$$
Ainsi :
$\begin{array}{rcl} h(21)&=&h(3\times 7)\\\\&=&3\times h(7)\\\\&=&3\times(-14)\\\\&=&-42\end{array}$
Donc, $\boxed{h(21)=-42}$
$-\ $ calcul de $h(-28)$
On sait que : $-28=-4\times 7$
Alors, on a : $h(-28)=h(-4\times 7)$
D'après une propriété de la linéarité, on a :
$$h(-4\times 7)=-4\times h(7)$$
On obtient alors :
$\begin{array}{rcl} h(-28)&=&h(-4\times 7)\\\\&=&-4\times h(7)\\\\&=&-4\times(-14)\\\\&=&56\end{array}$
Donc, $\boxed{h(-28)=56}$
$-\ $ calcul de $h(11)$
On remarque que : $11=7-(-4)$
Ce qui donne alors : $h(11)=h(7-(-4))$
Or, d'après une propriété de la linéarité, on a :
$$h(7-(-4))=h(7)-h(-4)$$
Ainsi, on a :
$\begin{array}{rcl} h(11)&=&h(7-(-4))\\\\&=&h(7)-h(-4)\\\\&=&-14-8\\\\&=&-22\end{array}$
D'où, $\boxed{h(11)=-22}$
Exercice 19
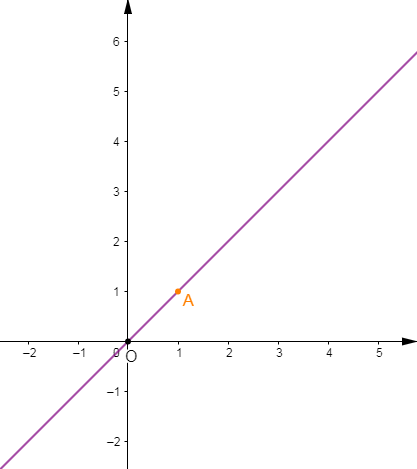
Représentons graphiquement l'application linéaire $m$ définie par $m(x)=x.$
On a : $m(x)=x=1\times x.$
Donc, le coefficient de linéarité de $m$ est égal à $1.$
Ainsi, sa représentation graphique est une droite qui passe par $O$ ; origine du repère et par le point $A\begin{pmatrix} 1\\1\end{pmatrix}.$
On place alors le point $A\begin{pmatrix} 1\\1\end{pmatrix}$ puis, on trace la droite passant par $O\ $ et $\ A.$

Exercice 20
On considère l'application linéaire $g$ telle que $g(11)=66\;;\ g(5)=30.$
1) Sans calculer le coefficient, calculons $g(16)\;;\ g(22)\;;\ g(15).$
$-\ $ calcul de $g(16)$
On sait que : $16=11+5$
Alors, on peut écrire : $g(16)=g(11+5)$
Or, d'après une propriété de la linéarité, on a :
$$g(11+5)=g(11)+g(5)$$
On obtient :
$\begin{array}{rcl} g(16)&=&g(11+5)\\\\&=&g(11)+g(5)\\\\&=&66+30\\\\&=&96\end{array}$
Ainsi, $\boxed{g(16)=96}$
$-\ $ calcul de $g(22)$
On a : $22=2\times 11$
Donc, on peut écrire : $g(22)=g(2\times 11)$
En appliquant une propriété de la linéarité, on obtient :
$$g(2\times 11)=2\times g(11)$$
On a alors :
$\begin{array}{rcl} g(22)&=&g(2\times 11)\\\\&=&2\times g(11)\\\\&=&2\times 66\\\\&=&132\end{array}$
D'où, $\boxed{g(22)=132}$
$-\ $ calcul de $g(15)$
On sait que : $15=3\times 5$
Alors, on peut écrire : $g(15)=g(3\times 5)$
Or, en appliquant une propriété de la linéarité, on obtient :
$$g(3\times 5)=3\times g(5)$$
Ainsi, on a :
$\begin{array}{rcl} g(15)&=&g(3\times 5)\\\\&=&3\times g(5)\\\\&=&3\times 30\\\\&=&90\end{array}$
Donc, $\boxed{g(15)=90}$
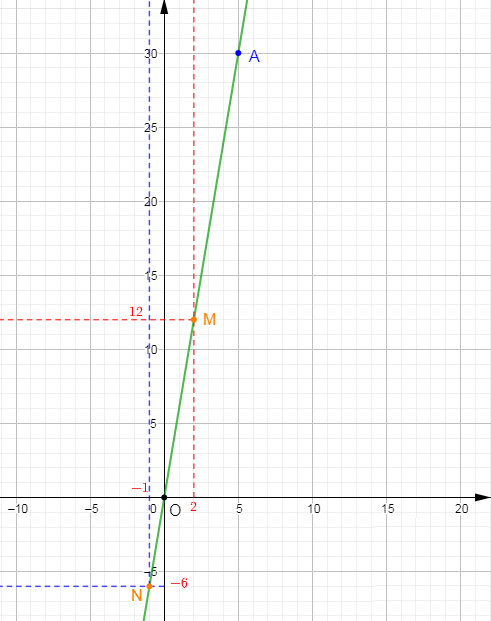
2) Représentons graphiquement l'application $g.$
Comme $g$ est une application linéaire alors, sa représentation graphique est une droite qui passe par l'origine $O$ du repère.
Par ailleurs, on sait que : $g(5)=30$
Cela signifie que l'image de $5$ par $g$ est égale à $30.$
D'où, le point $A\begin{pmatrix} 5\\30\end{pmatrix}$ appartient à cette droite.
Donc, on place le point $A$ puis, on trace la droite passant par $O\ $ et $\ A.$
3) Déterminons graphiquement l'ordonnée du point $M$ d'abscisse $2.$
Pour cela, on se place sur l'axe des abscisses à la valeur $2$ puis, on trace une droite verticale.
Cette droite coupe la droite qui représente l'application $g$ au point $M.$
Ensuite, à partir de $M$, on trace une autre droite horizontale.
On constate que cette droite horizontale coupe l'axe des ordonnées à la valeur $12.$
Par conséquent, $12$ l'ordonnée du point $M$ d'abscisse $2.$
4) Déterminons graphiquement l'abscisse du point $N$ d'ordonnée $-6.$
On se place sur l'axe des ordonnées à la valeur $-6$ puis, on trace une droite horizontale.
Cette droite coupe la droite qui représente l'application $g$ au point $N.$
Ensuite, à partir de ce point $N$, on trace une autre droite verticale.
On constate que cette droite verticale coupe l'axe des abscisses à la valeur $-1.$
Par conséquent, $-1$ l'abscisse du point $N$ d'ordonnée $-6.$

Auteur:
Diny Faye

Commentaires
hannieltougma@g... (non vérifié)
dim, 07/04/2021 - 18:00
Permalien
les exercices sont très
Ajouter un commentaire