Vous êtes ici

Solution des exercices : Inéquations et Systèmes d'inéquations à deux inconnues 3e

Classe:

Troisième

Exercice 1

1) Parmi les couples

$(2\;;\ 1)\;;\ (-2\;;\ 0)\$ et

$\ (-4\;;\ 1)$ déterminons ceux qui sont solution de l'inéquation :

$2x-y+2\leq 0$

En effet,

$(2\;;\ 1)$ est solution de

$2x-y+2\leq 0\$ si, et seulement si, le couple

$(2\;;\ 1)$ vérifie l'inéquation.

Ainsi, en remplaçant

$x$ par

$2\$ et

$\ y$ par

$1$ dans l'inéquation, on obtient :

$2\times 2-1+2\leq 0$ si, et seulement si,

$5\leq 0.$ Ce qui est impossible.

Donc, le couple

$(2\;;\ 1)$ n'est pas solution de l'inéquation

$2x-y+2\leq 0$

$(-2\;;\ 0)$ est solution de

$2x-y+2\leq 0\$ si, et seulement si, le couple

$(-2\;;\ 0)$ vérifie l'inéquation.

Remplaçons alors

$x$ par

$-2\$ et

$\ y$ par

$0$ dans l'inéquation.

On a :

$2\times(-2)-0+2\leq 0$ si, et seulement si,

$-2\leq 0.$ Ce qui est toujours vrai.

Par conséquent, le couple

$(-2\;;\ 0)$ est solution de l'inéquation

$2x-y+2\leq 0$

$(-4\;;\ 1)$ est solution de

$2x-y+2\leq 0\$ si, et seulement si, le couple

$(-4\;;\ 1)$ vérifie l'inéquation.

Ainsi, en remplaçant

$x$ par

$-4\$ et

$\ y$ par

$1$ dans l'inéquation, on obtient :

$2\times(-4)-1+2\leq 0$ si, et seulement si,

$-7\leq 0.$ Ce qui est toujours vrai.

Donc, le couple

$(-4\;;\ 1)$ est solution de l'inéquation

$2x-y+2\leq 0$

2) Parmi les couples

$(2\;;\ 4)\;;\ (-3\;;\ 2)\$ et

$\ (-4\;;\ 1)$ déterminons ceux qui sont solution du système :

$\left\lbrace\begin{array}{rcl} x+y-2&>&0\\\\2x-y&\leq&1\end{array}\right.$

En effet,

$(2\;;\ 4)$ est solution du système

$\left\lbrace\begin{array}{rcl} x+y-2&>&0\\\\2x-y&\leq&1\end{array}\right.$ si, et seulement si, le couple

$(2\;;\ 4)$ vérifie chacune des inéquations du système.

Remplaçons alors

$x$ par

$2\$ et

$\ y$ par

$4$ dans la première inéquation.

On a :

$2+4-2>0$ si, et seulement si,

$4>0.$ Ce qui est toujours vrai.

Donc, le couple

$(2\;;\ 4)$ vérifie la première inéquation du système.

De la même manière, en remplaçant

$x$ par

$2\$ et

$\ y$ par

$4$ dans la deuxième inéquation, on obtient :

$2\times 2-4\leq 1$ si, et seulement si

$0\leq 1.$ Ce qui est toujours vrai.

Ce qui signifie donc que le couple

$(2\;;\ 4)$ vérifie la deuxième inéquation du système.

Ainsi, le couple

$(2\;;\ 4)$ vérifie chacune des inéquations du système.

Par conséquent,

$(2\;;\ 4)$ est solution du système

$\left\lbrace\begin{array}{rcl} x+y-2&>&0\\\\2x-y&\leq&1\end{array}\right.$

$(-3\;;\ 2)$ est solution du système

$\left\lbrace\begin{array}{rcl} x+y-2&>&0\\\\2x-y&\leq&1\end{array}\right.$ si, et seulement si, le couple

$(-3\;;\ 2)$ vérifie chacune des inéquations du système.

En remplaçant

$x$ par

$-3\$ et

$\ y$ par

$2$ , dans la première inéquation, on obtient :

$-3+2-2>0$ si, et seulement si,

$-3>0.$ Ce qui est impossible.

Ce qui signifie donc que le couple

$(-3\;;\ 2)$ ne vérifie pas la première inéquation du système.

Par conséquent,

$(-3\;;\ 2)$ n'est pas solution du système.

$(-4\;;\ 1)$ est solution du système

$\left\lbrace\begin{array}{rcl} x+y-2&>&0\\\\2x-y&\leq&1\end{array}\right.$ si, et seulement si, le couple

$(-4\;;\ 1)$ vérifie chacune des inéquations du système.

Remplaçons alors

$x$ par

$-4\$ et

$\ y$ par

$1$ , dans la première inéquation.

On a :

$-4+1-2>0$ si, et seulement si,

$-5>0.$ Ce qui est impossible.

Donc, le couple

$(-4\;;\ 1)$ ne vérifie pas la première inéquation du système.

Par conséquent,

$(-4\;;\ 1)$ n'est pas solution du système.

Exercice 2

Représentons graphiquement l'ensemble des solutions des inéquations suivantes :

$x+y-1\leq 0$

Représentons d'abord la droite

$(D)$ d'équation

$x+y-1=0.$

Pour cela, choisissons deux points

$A\$ et

$\ B$ dont les coordonnées vérifient l'équation de la droite

$(D).$

Soit :

$\begin{array}{|c|c|c|}\hline&A&B\\\hline x&0&1\\\hline y&1&0\\\hline\end{array}$

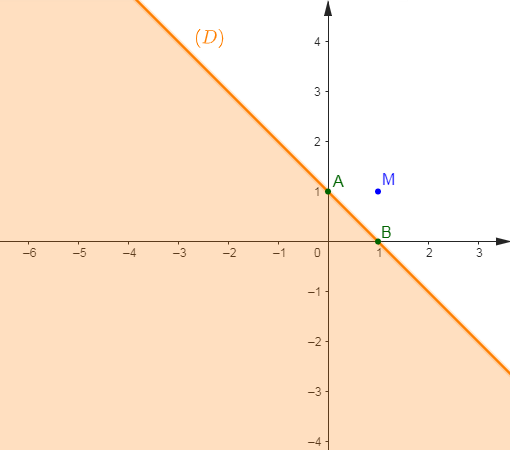
$(D)$ est donc la droite passant par les points

$A(0\;;\ 1)\$ et

$\ B(1\;;\ 0).$

Choisissons ensuite un point

$M$ n'appartenant pas à

$(D)$ comme point de vérification.

C'est-à-dire ; un point

$M$ dont les coordonnées ne vérifient pas l'équation de

$(D).$

Soit alors :

$M(1\;;\ 1)$

Cherchons enfin le demi-plan dans lequel appartient ce point

$M.$

En remplaçant les coordonnées du point

$M$ dans l'inéquation, on obtient :

$1+1-1\leq 0$ si, et seulement si,

$1\leq 0.$ Ce qui est impossible.

Ce qui signifie donc que les coordonnées de

$M$ ne vérifient pas l'inéquation

$x+y-1\leq 0.$

Ainsi,

$M$ n'appartient pas au demi-plan solution.

D'où, l'ensemble des solutions de l'inéquation

$x+y-1\leq 0$ constitue la partie du graphique ci-dessous coloriée en orange.

$3x+2y>0$

Représentons d'abord la droite

$(D')$ d'équation

$3x+2y=0.$

Pour cela, choisissons deux points

$O\$ et

$\ C$ dont les coordonnées vérifient l'équation de la droite

$(D').$

Soit :

$\begin{array}{|c|c|c|}\hline&O&C\\\hline x&0&2\\\hline y&0&-3\\\hline\end{array}$

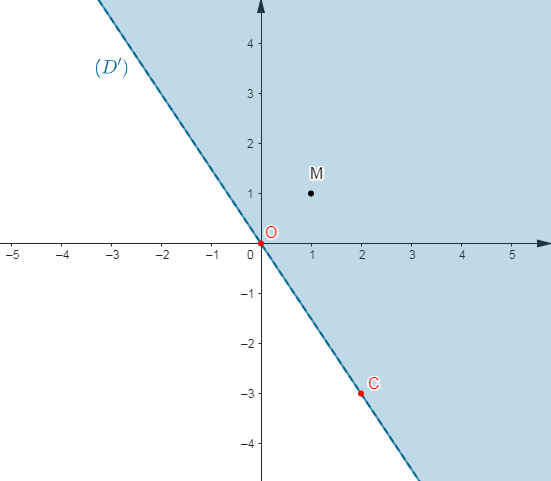
$(D')$ est donc la droite passant par l'origine

$O$ du repère et par le point

$C(2\;;\ -3).$

Choisissons ensuite un point

$M$ n'appartenant pas à

$(D')$ comme point de vérification.

Soit :

$M(1\;;\ 1)$

Cherchons enfin le demi-plan dans lequel appartient ce point

$M.$

En remplaçant les coordonnées du point

$M$ dans l'inéquation, on obtient :

$3\times 1+2\times 1>0$ si, et seulement si,

$5>0.$ Ce qui est toujours vrai.

Ce qui veut dire que les coordonnées de

$M$ vérifient l'inéquation

$3x+2y>0.$

Donc,

$M$ appartient au demi-plan solution.

Par conséquent, l'ensemble des solutions de l'inéquation

$3x+2y>0$ est la partie du graphique ci-dessous coloriée en bleu et privée de la droite

$(D').$

Exercice 3

Résolvons graphiquement les systèmes d'inéquations suivants :

$\left\lbrace\begin{array}{rcl} x+y-2&<&0\\\\x+y+4&>&0\end{array}\right.$

On cherchera d'abord, pour chacune des inéquations du système, le demi-plan solution.

Soit les droites

$(\Delta_{1})\$ et

$\ (\Delta_{2})$ d'équations respectives :

$(\Delta_{1})\ :\ x+y-2=0$

$(\Delta_{2})\ :\ x+y+4=0$

Représentons alors ces deux droites.

Soit deux points

$A\$ et

$\ B$ appartenant à la droite

$(\Delta_{1}).$

On a :

$\begin{array}{|c|c|c|}\hline&A&B\\\hline x&0&2\\\hline y&2&0\\\hline\end{array}$

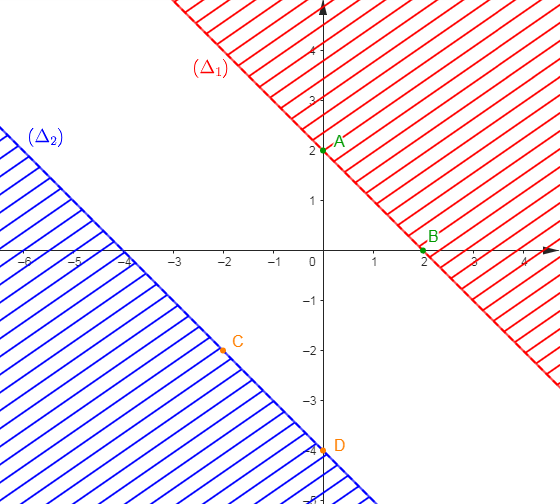
$(\Delta_{1})$ est donc la droite passant par les points

$A(0\;;\ 2)\$ et

$\ B(2\;;\ 0).$

Soit

$C\$ et

$\ D$ deux points appartenant à la droite

$(\Delta_{2}).$

On a :

$\begin{array}{|c|c|c|}\hline&C&D\\\hline x&-2&0\\\hline y&-2&-4\\\hline\end{array}$

$(\Delta_{2})$ est donc la droite passant par les points

$C(-2\;;\ -2)\$ et

$\ D(0\;;\ -4).$

On remarque que le point

$O\begin{pmatrix} 0\\\\0\end{pmatrix}$ n'appartient ni à

$(\Delta_{1})$ ni à

$(\Delta_{2}).$

Donc, on peut choisir l'origine

$O$ du repère comme point de vérification.

Alors, remplaçons les coordonnées du point

$O$ dans l'inéquation

$x+y-2<0.$

On a :

$0+0-2<0$ si, et seulement si,

$-2<0.$ Ce qui est toujours vrai.

Ce qui signifie donc que les coordonnées de

$O$ vérifient l'inéquation

$x+y-2<0.$

Ainsi,

$O$ appartient au demi-plan solution de cette inéquation.

C'est la partie du graphique non hachurée en rouge et privée de la droite

$(\Delta_{1}).$

De la même manière, en remplaçant les coordonnées du point

$O$ dans l'inéquation

$x+y+4>0$ , on obtient :

$0+0+4>0$ si, et seulement si,

$4>0.$ Ce qui est toujours vrai.

Donc, les coordonnées de

$O$ vérifient l'inéquation

$x+y+4>0.$

Par suite,

$O$ appartient au demi-plan solution de cette inéquation.

C'est la partie du graphique non hachurée en bleu et privée de la droite

$(\Delta_{2}).$

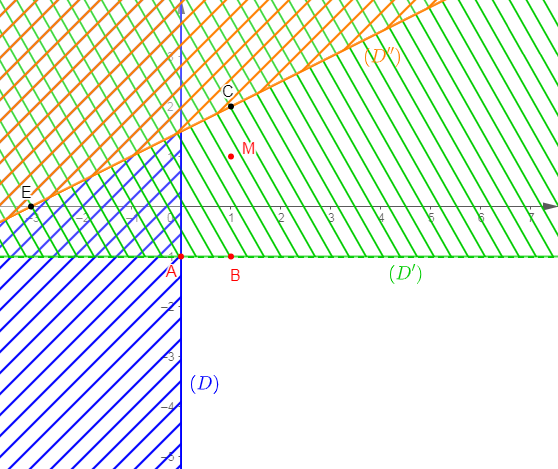
Par conséquent, l'ensemble des solutions du système d'inéquations

$\left\lbrace\begin{array}{rcl} x+y-2&<&0\\\\x+y+4&>&0\end{array}\right.$ est la partie non hachurée du graphique ci-dessous privée des droites

$(\Delta_{1})\$ et

$\ (\Delta_{2}).$

$\left\lbrace\begin{array}{rcl} 2x-y&<&1\\\\x-2y&>&-4\end{array}\right.$

Ce système peut encore s'écrire :

$\left\lbrace\begin{array}{rcl} 2x-y-1&<&0\\\\x-2y+4&>&0\end{array}\right.$

Cherchera d'abord, pour chacune des inéquations du système, le demi-plan solution.

Soit les droites

$(D_{1})\$ et

$\ (D_{2})$ d'équations respectives :

$(D_{1})\ :\ 2x-y-1=0$

$(D_{2})\ :\ x-2y+4=0$

Représentons alors ces deux droites.

Soit

$A\$ et

$\ B$ deux points appartenant à la droite

$(D_{1}).$

On a :

$\begin{array}{|c|c|c|}\hline&A&B\\\hline x&0&1\\\hline y&-1&1\\\hline\end{array}$

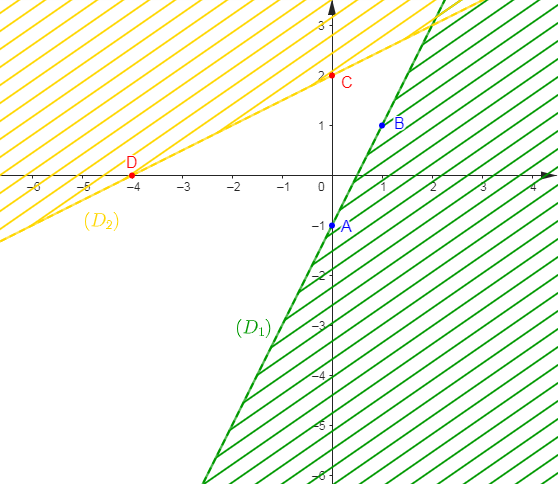
$(D_{1})$ est donc la droite passant par les points

$A(0\;;\ -1)\$ et

$\ B(1\;;\ 1).$

Soit

$C\$ et

$\ D$ deux points appartenant à la droite

$(D_{2}).$

On a :

$\begin{array}{|c|c|c|}\hline&C&D\\\hline x&0&-4\\\hline y&2&0\\\hline\end{array}$

$(D_{2})$ est donc la droite passant par les points

$C(0\;;\ 2)\$ et

$\ D(-4\;;\ 0).$

Nous constatons que le point

$O(0\;;\ 0)$ n'appartient ni à

$(D_{1})$ ni à

$(D_{2}).$

Donc, choisissons le point

$O$ origine du repère comme point de vérification.

Alors, remplaçons les coordonnées du point

$O$ dans l'inéquation

$2x-y-1<0.$

On a :

$2\times 0-0-1<0$ si, et seulement si,

$-1<0.$ Ce qui est toujours vrai.

Donc, les coordonnées de

$O$ vérifient l'inéquation

$2x-y-1<0.$

Ainsi,

$O$ appartient au demi-plan solution de cette inéquation.

Cette solution est alors représentée par la partie du graphique non hachurée en vert et privée de la droite

$(D_{1}).$

Ensuite, en remplaçant les coordonnées du point

$O$ dans l'inéquation

$x-2y+4>0$ , on obtient :

$0-2\times 0+4>0$ si, et seulement si,

$4>0.$ Ce qui est toujours vrai.

Donc, les coordonnées de

$O$ vérifient l'inéquation

$x-2y+4>0.$

Ce qui signifie que le point

$O$ appartient au demi-plan solution de cette inéquation.

C'est la partie du graphique non hachurée en jaune et privée de la droite

$(D_{2}).$

Ainsi, l'ensemble des solutions du système d'inéquations

$\left\lbrace\begin{array}{rcl} 2x-y&<&1\\\\x-2y&>&-4\end{array}\right.$ est la partie non hachurée du graphique ci-dessous privée des droites

$(D_{1})\$ et

$\ (D_{2}).$

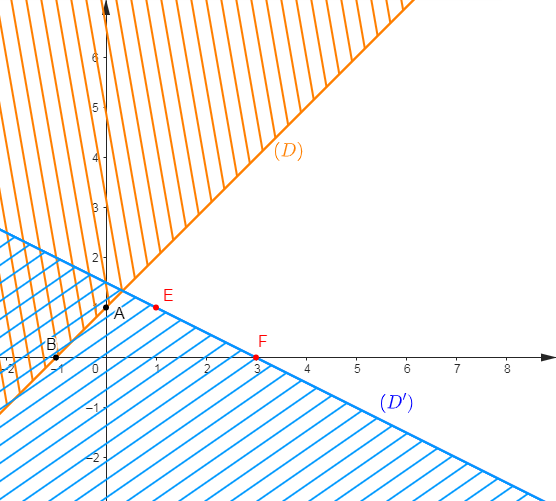
$\left\lbrace\begin{array}{rcl} x-y+1&\geq&0\\\\x+2y-3&\geq&0\end{array}\right.$

On cherchera d'abord, pour chacune des inéquations du système, le demi-plan solution.

Considérons les droites

$(D)\$ et

$\ (D')$ d'équations respectives :

$(D)\ :\ x-y+1=0$

$(D')\ :\ x+2y-3=0$

Représentons alors ces deux droites.

Soit

$A\$ et

$\ B$ deux points de

$(D).$

On a :

$\begin{array}{|c|c|c|}\hline&A&B\\\hline x&0&-1\\\hline y&1&0\\\hline\end{array}$

$(D)$ est donc la droite passant par les points

$A(0\;;\ 1)\$ et

$\ B(-1\;;\ 0).$

Soit

$E\$ et

$\ F$ deux points appartenant à

$(D').$

On a :

$\begin{array}{|c|c|c|}\hline&E&F\\\hline x&1&3\\\hline y&1&0\\\hline\end{array}$

$(D')$ est donc la droite passant par les points

$E(1\;;\ 1)\$ et

$\ F(3\;;\ 0).$

Nous remarquons que les coordonnées du point

$O$ origine du repère ne vérifient pas les équations de

$(D)$ et de

$(D').$

Donc, on peut choisir le point

$O$ comme point de vérification.

Alors, en remplaçant les coordonnées du point

$O$ dans l'inéquation

$x-y+1\geq 0$ , on obtient :

$0-0+1\geq 0$ si, et seulement si,

$1\geq 0.$ Ce qui est toujours vrai.

Donc, les coordonnées de

$O$ vérifient l'inéquation

$x-y+1\geq 0.$

Ce qui veut dire que

$O$ appartient au demi-plan solution de cette inéquation.

Cette solution est alors représentée par la partie du graphique non hachurée en orange.

Ensuite, en remplaçant les coordonnées du point

$O$ dans l'inéquation

$x+2y-3\geq 0$ , on obtient :

$0+2\times 0-3\geq 0$ si, et seulement si,

$-3\geq 0.$ Ce qui est impossible.

Donc, les coordonnées de

$O$ ne vérifient pas l'inéquation

$x+2y-3\geq 0.$

Ce qui signifie que le point

$O$ n'appartient pas au demi-plan solution de cette inéquation.

Alors, le demi-plan solution est cette partie du graphique non hachurée en bleu.

Par conséquent, l'ensemble des solutions du système d'inéquations

$\left\lbrace\begin{array}{rcl} x-y+1&\geq&0\\\\x+2y-3&\geq&0\end{array}\right.$ est la partie non hachurée du graphique ci-dessous.

$\left\lbrace\begin{array}{rcl} x&\geq&0\\\\y+1&<&0\\\\x-2y+3&\geq&0\end{array}\right.$

Cherchons d'abord, pour chacune des inéquations du système, le demi-plan solution.

Soit :

$(D)\;,\ (D')\$ et

$\ (D'')$ les droites d'équations respectives :

$(D)\ :\ x=0$

$(D')\ :\ y+1=0$

$(D'')\ :\ x-2y+3=0$

Représentons alors ces trois droites.

En effet,

$(D)$ représente l'axe des ordonnées.

Soit

$A\$ et

$\ B$ deux points de

$(D').$

On a :

$\begin{array}{|c|c|c|}\hline&A&B\\\hline x&0&1\\\hline y&-1&-1\\\hline\end{array}$

$(D')$ est donc la droite passant par les points

$A(0\;;\ -1)\$ et

$\ B(1\;;\ -1).$

Soit

$C\$ et

$\ E$ deux points appartenant à

$(D'').$

On a :

$\begin{array}{|c|c|c|}\hline&C&E\\\hline x&1&-3\\\hline y&2&0\\\hline\end{array}$

$(D'')$ est donc la droite passant par les points

$C(1\;;\ 2)\$ et

$\ E(-3\;;\ 0).$

Choisissons ensuite un point

$M$ n'appartenant pas à ces trois droites comme point de vérification.

Soit :

$M(1\;;\ 1)$

Alors, en remplaçant les coordonnées du point

$M$ dans l'inéquation

$x\geq 0$ , on obtient :

$1\geq 0.$ Ce qui est toujours vrai.

Donc, les coordonnées de

$M$ vérifient l'inéquation

$x\geq 0.$

Ce qui signifie que

$M$ appartient au demi-plan solution de cette inéquation et cette solution est représentée par la partie du graphique non hachurée en bleu.

Remplaçons encore les coordonnées du point

$M$ dans l'inéquation

$y+1<0.$

On a :

$1+1<0$ si, et seulement si,

$2<0.$ Ce qui est impossible.

Donc, les coordonnées de

$M$ ne vérifient pas l'inéquation

$y+1<0.$

Ce qui veut dire que

$M$ n'appartient pas au demi-plan solution de cette inéquation.

Cette solution est représentée par la partie du graphique non hachurée en vert privée de la droite

$(D').$

En remplaçant les coordonnées du point

$M$ dans l'inéquation

$x-2y+3\geq 0$ , on obtient :

$1-2\times 1+3\geq 0$ si, et seulement si,

$2\geq 0.$ Ce qui est toujours vrai.

Donc, les coordonnées de

$M$ vérifient l'inéquation

$x-2y+3\geq 0.$

Ainsi,

$M$ appartient au demi-plan solution de cette inéquation et cette solution est représentée par la partie du graphique non hachurée en orange.

Par conséquent, l'ensemble des solutions du système d'inéquations

$\left\lbrace\begin{array}{rcl} x&\geq&0\\\\y+1&<&0\\\\x-2y+3&\geq&0\end{array}\right.$ est la partie non hachurée du graphique ci-dessous privée de la droite

$(D').$

$\left\lbrace\begin{array}{rcl} 5x+y-1&<&0\\\\x+y+3&\geq&0\end{array}\right.$

Cherchons d'abord, pour chacune des inéquations du système, le demi-plan solution.

Considérons les droites

$(D_{1})\$ et

$\ (D_{2})$ d'équations respectives :

$(D_{1})\ :\ 5x+y-1=0$

$(D_{2})\ :\ x+y+3=0$

Représentons alors ces deux droites dans un repère.

Choisissons ensuite un point de vérification.

En effet, nous remarquons que les coordonnées du point

$O$ origine du repère ne vérifient pas les équations de

$(D_{1})$ et de

$(D_{2}).$

Donc, on peut choisir le point

$O$ comme point de vérification.

Alors, en remplaçant les coordonnées du point

$O$ dans l'inéquation

$5x+y-1<0$ , on obtient :

$5\times 0+0-1<0$ si, et seulement si,

$-1<0.$ Ce qui est toujours vrai.

Donc, les coordonnées de

$O$ vérifient l'inéquation

$5x+y-1<0.$

Ce qui veut dire que

$O$ appartient au demi-plan solution de cette inéquation et cette solution est alors représentée par la partie du graphique non hachurée en rouge privée de la droite

$(D_{1}).$

Remplaçons encore les coordonnées du point

$O$ dans l'inéquation

$x+y+3\geq 0.$

On a :

$0+0+3\geq 0$ si, et seulement si,

$3\geq 0.$ Ce qui est toujours vrai.

Donc, les coordonnées de

$O$ vérifient l'inéquation

$x+y+3\geq 0.$

Ce qui signifie que le point

$O$ appartient au demi-plan solution de cette inéquation.

Alors, le demi-plan solution est cette partie du graphique non hachurée en bleu.

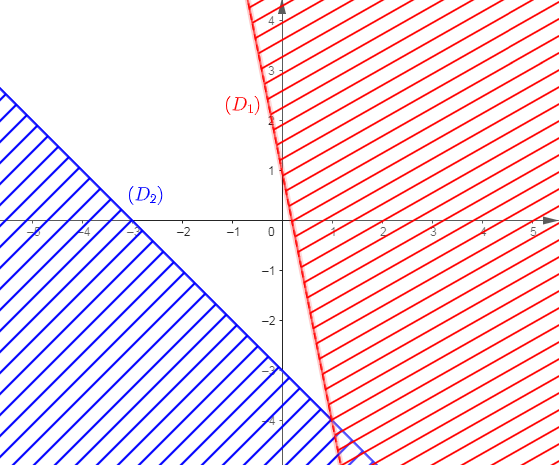
Par conséquent, l'ensemble des solutions du système d'inéquations

$\left\lbrace\begin{array}{rcl} 5x+y-1&<&0\\\\x+y+3&\geq&0\end{array}\right.$ est la partie non hachurée du graphique ci-dessous privée de la droite

$(D_{1}).$

$\left\lbrace\begin{array}{rcl} 4x+y+2&\geq&0\\\\-2x+y&<&-3\end{array}\right.$

Ce système peut encore s'écrire :

$\left\lbrace\begin{array}{rcl} 4x+y+2&\geq&0\\\\-2x+y+3&<&0\end{array}\right.$

Cherchons d'abord, pour chacune des inéquations du système, le demi-plan solution.

Pour cela, représentons dans un même repère les droites

$(D_{1})\$ et

$\ (D_{2})$ d'équations respectives :

$(D_{1})\ :\ 4x+y+2=0$

$(D_{2})\ :\ -2x+y+3=0$

Choisissons ensuite un point de vérification.

En effet, nous remarquons que les coordonnées du point

$O$ origine du repère ne vérifient pas les équations de

$(D_{1})$ et de

$(D_{2}).$

Donc, on peut choisir le point

$O$ comme point de vérification.

Ainsi, en remplaçant les coordonnées du point

$O$ dans l'inéquation

$4x+y+2\geq 0$ , on obtient :

$4\times 0+0+2\geq 0$ si, et seulement si,

$2\geq 0.$ Ce qui est toujours vrai.

Donc, les coordonnées de

$O$ vérifient l'inéquation

$4x+y+2\geq 0.$

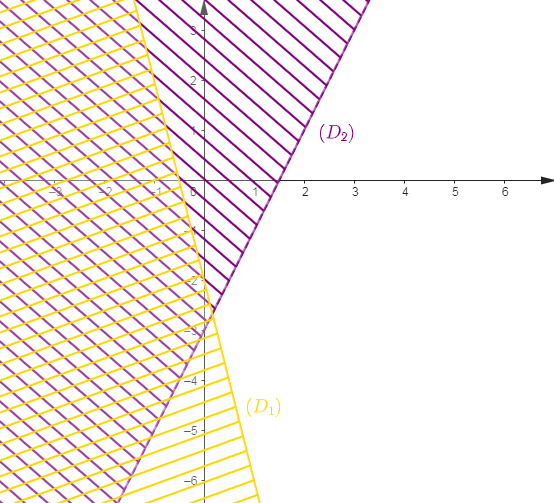
Ce qui veut dire que

$O$ appartient au demi-plan solution de cette inéquation et cette solution est alors représentée par la partie du graphique non hachurée en jaune.

De la même manière, en remplaçant les coordonnées du point

$O$ dans l'inéquation

$-2x+y+3<0$ , on obtient :

$-2\times 0+0+3<0$ si, et seulement si,

$3<0.$ Ce qui est impossible.

Donc, les coordonnées de

$O$ ne vérifient pas l'inéquation

$-2x+y+3<0.$

Cela signifie que

$O$ n'appartient pas au demi-plan solution de cette inéquation.

Cette solution est alors représentée par la partie du graphique non hachurée en violet privée de la droite

$(D_{2}).$

Ainsi, l'ensemble des solutions du système d'inéquations

$\left\lbrace\begin{array}{rcl} 4x+y+2&\geq&0\\\\-2x+y&<&-3\end{array}\right.$ est la partie non hachurée du graphique ci-dessous privée de la droite

$(D_{2}).$

Exercice 4

Le plan est muni d'un R.O.N

$(D)\ :\ y=-2x+1\$ et

$\ (D')\ :\ y+x=0.$

1) Montrons que

$(D)\$ et

$\ (D')$ sont sécantes.

En effet, l'équation de droite

$(D')$ peut encore s'écrire :

$y=-x.$

Ainsi :

$(D)$ a pour coefficient directeur

$-2$

$(D')$ a pour coefficient directeur

$-1$

On remarque alors que les droites

$(D)\$ et

$\ (D')$ n'ont pas le même coefficient directeur.

Ce qui signifie qu'elles ne sont pas parallèles.

Par conséquent,

$(D)\$ et

$\ (D')$ sont sécantes.

Par ailleurs, ces deux droites ne sont pas perpendiculaires car, le produit de leur coefficient directeur n'est pas égal à

$-1.$

2) Traçons les droites

$(D)\$ et

$\ (D')$

On remarque d'abord que

$(D')$ est une représentation d'une application linéaire donc, elle passe par l'origine du repère.

Choisissons alors deux points

$A\;,\ B$ appartenant à

$(D)$ et un point

$C$ appartenant à

$(D').$

Soit :

$\begin{array}{|c|c|c|}\hline&A&B \\ \hline x&2&0 \\ \hline y&-3&1 \\ \hline \end{array}\qquad\qquad \begin{array}{|c|c|}\hline&C \\ \hline x&2 \\ \hline y&-2 \\ \hline\end{array}$

Traçons ensuite la droite

$(D)$ passant par

$A\;,\ B\$ et la droite

$(D')$ passant par

$C$ et par

$O$ ; origine du repère.

3) Déterminons le point d'intersection de

$(D)\$ et

$\ (D').$

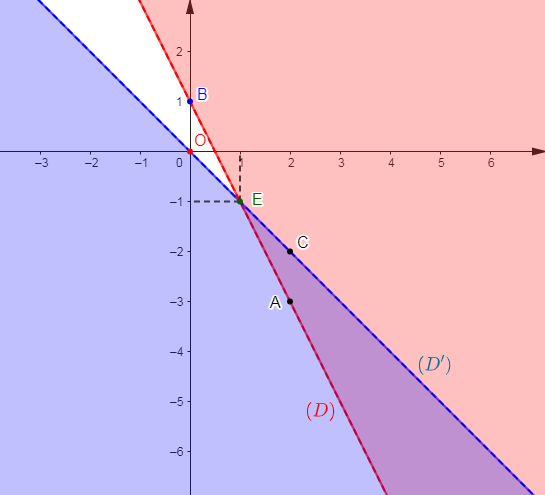
En observant le graphique, nous constatons que les

$(D)\$ et

$\ (D')$ se coupent au point

$E.$

Alors, en projetant orthogonalement ce point sur les axes du repère, on trouve les coordonnées de

$E$ données par :

$E(1\;;\ -1)$

Autre méthode :

On peut aussi trouver les coordonnées du point d'intersection de

$(D)\$ et

$\ (D')$ en résolvant le système d'équations formé des équations de

$(D)\$ et

$\ (D').$

Soit :

$\left\lbrace\begin{array}{rcl} y+2x-1&=&0\\\\y+x&=&0\end{array}\right.$

Ce qui est équivalent à :

$\left\lbrace\begin{array}{rclr} y+2x-1&=&0&\qquad(1)\\\\y&=&-x&\qquad(2)\end{array}\right.$

Alors, dans l'équation

$(1)$ , en remplaçant

$y$ par

$-x$ , on obtient :

$\begin{array}{rcl} y+2x-1=0&\Rightarrow&-x+2x-1=0\\\\&\Rightarrow&x-1=0\\\\&\Rightarrow&x=1\end{array}$

Dans l'équation

$(2)$ , en remplaçant cette valeur de

$x$ , on trouve :

$y=-1$

Ainsi,

$\boxed{E(1\;;\ -1)}$

4) Résolvons graphiquement le système :

$\left\lbrace\begin{array}{rcl} y+2x-1&>&0\\\\y+x&<&0\end{array}\right.$

Sur le graphique, on constate que le point

$C(2\;;\ -2)$ n'est pas sur la droite

$(D)$ d'équation

$y+2x-1=0.$

Donc, nous choisissons

$C$ comme point de vérification de l'inéquation

$y+2x-1>0.$

Alors, en remplaçant les coordonnées de

$C$ dans l'inéquation

$y+2x-1>0$ , obtient :

$-2+2\times 2-1>0$ si, et seulement si,

$1>0.$ Ce qui est toujours vrai.

Ainsi, les coordonnées du point

$C$ vérifient l'inéquation :

$y+2x-1>0$

Ce qui signifie que le point

$C$ appartient à la solution de cette inéquation représentée par la partie coloriée en rouge privée de la droite

$(D).$

En observant encore le graphique, nous remarquons que le point

$B(0\;;\ 1)$ n'est pas sur la droite

$(D')$ d'équation

$y+x=0.$

Donc, nous choisissons

$B$ comme point de vérification de l'inéquation

$y+x<0.$

En remplaçant alors ses coordonnées dans l'inéquation

$y+x<0$ , on a :

$1+0<0$ si, et seulement si,

$1<0.$ Ce qui est impossible.

Alors, les coordonnées du point

$B$ ne vérifient pas l'inéquation :

$y+x<0$

Ce qui signifie que le point

$B$ n'appartient pas à la solution de cette inéquation représentée par la partie coloriée en bleu privée de la droite

$(D').$

Par conséquent, la solution du système

$\left\lbrace\begin{array}{rcl} y+2x-1&>&0\\\\y+x&<&0\end{array}\right.$ est la partie coloriée à la fois en bleu et en rouge.

Elle est donc représentée par le secteur angulaire colorié en violet privé des droites

$(D)\$ et

$\ (D').$

Exercice 5

Soit l'inéquation :

$-2x+5y\leq 3$

1) Parmi les couples de nombres réels suivants donnons ceux qui sont solutions de l'inéquation en justifiants notre réponse :

$(2\;;\ 1)\;,\ \left(-\dfrac{1}{2}\;;\ 2\right)\;,\ (1\;;\ 1)$

$(2\;;\ 1)$ est solution de

$-2x+5y\leq 3$ si, et seulement si, le couple

$(2\;;\ 1)$ vérifie l'inéquation.

Alors, en remplaçant

$x$ par

$2\$ et

$\ y$ par

$1$ dans l'inéquation, on obtient :

$-2\times 2+5\times 1\leq 3$ si, et seulement si,

$1\leq 3.$ Ce qui est toujours vrai.

Donc, le couple

$(2\;;\ 1)$ est solution de l'inéquation

$-2x+5y\leq 3.$

$\left(-\dfrac{1}{2}\;;\ 2\right)$ est solution de

$-2x+5y\leq 3$ si, et seulement si, le couple

$(2\;;\ 1)$ vérifie l'inéquation.

Remplaçons alors

$x$ par

$-\dfrac{1}{2}\$ et

$\ y$ par

$2$ dans l'inéquation

$-2x+5y\leq 3.$

On a :

$-2\times\left(-\dfrac{1}{2}\right) +5\times 2\leq 3$ si, et seulement si,

$11\leq 3.$ Ce qui est impossible.

Par conséquent, le couple

$\left(-\dfrac{1}{2}\;;\ 2\right)$ n'est pas solution de l'inéquation

$-2x+5y\leq 3.$

$(1\;;\ 1)$ est solution de

$-2x+5y\leq 3$ si, et seulement si, le couple

$(2\;;\ 1)$ vérifie l'inéquation.

Alors, en remplaçant

$x$ par

$1\$ et

$\ y$ par

$1$ dans l'inéquation, on obtient :

$-2\times 1+5\times 1\leq 3$ si, et seulement si,

$3\leq 3.$ Ce qui est toujours vrai.

D'où, le couple

$(1\;;\ 1)$ est solution de l'inéquation

$-2x+5y\leq 3.$

2) Déterminons les valeurs de

$a$ pour lesquelles le couple

$\left(\dfrac{a}{2}\;;\ -a\right)$ est solution de cette inéquation.

En effet,

$\left(\dfrac{a}{2}\;;\ -a\right)$ est solution de l'inéquation

$-2x+5y\leq 3$ si, et seulement si, le couple

$\left(\dfrac{a}{2}\;;\ -a\right)$ vérifie cette inéquation.

Alors, en remplaçant

$x$ par

$\left(\dfrac{a}{2}\right)\$ et

$\ y$ par

$-a$ dans l'inéquation, on obtient :

$\begin{array}{rcl} -2\times\left(\dfrac{a}{2}\right)+5\times(-a)\leq 3&\Leftrightarrow&-\dfrac{2a}{2}-5a\leq 3\\\\&\Leftrightarrow&-a-5a\leq 3\\\\&\Leftrightarrow&-6a\leq 3\\\\&\Leftrightarrow&a\geq\dfrac{3}{-6}\\\\&\Leftrightarrow&a\geq -\dfrac{1}{2}\end{array}$

Donc, le couple

$\left(\dfrac{a}{2}\;;\ -a\right)$ est solution de l'inéquation

$-2x+5y\leq 3$ si, et seulement si,

$a\geq -\dfrac{1}{2}.$

Ainsi, pour tout

$a\in\left[-\dfrac{1}{2}\;;\ +\infty\right[$ le couple

$\left(\dfrac{a}{2}\;;\ -a\right)$ est solution de l'inéquation

$-2x+5y\leq 3.$

3) Résolvons graphiquement cette inéquation.

Représentons d'abord la droite

$(D)$ d'équation

$-2x+5y=3.$

Cette équation peut encore s'écrire :

$(D)\ :\ -2x+5y-3=0$

Choisissons deux points

$A\$ et

$\ B$ dont les coordonnées vérifient l'équation de la droite

$(D).$

Soit :

$\begin{array}{|c|c|c|}\hline&A&B\\\hline x&1&6\\\hline y&1&3\\\hline\end{array}$

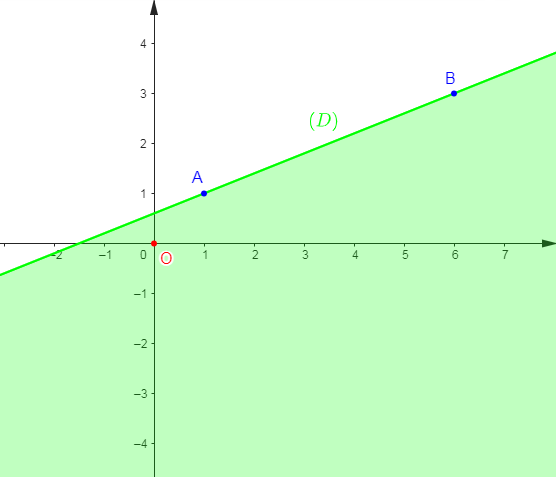
$(D)$ est donc la droite passant par les points

$A(1\;;\ 1)\$ et

$\ B(6\;;\ 3).$

Choisissons ensuite un point de vérification.

Comme les coordonnées du point

$O$ ne vérifient pas l'équation de

$(D)$ alors, nous choisissons

$O$ comme point de vérification.

Cherchons alors le demi-plan dans lequel appartient ce point

$M.$

En remplaçant les coordonnées du point

$O$ dans l'inéquation, on obtient :

$-2\times 0+5\times 0\leq 3$ si, et seulement si,

$0\leq 3.$ Ce qui est toujours vrai.

Cela signifie que les coordonnées de

$O$ vérifient l'inéquation

$-2x+5y\leq 3.$

D'où,

$O$ appartient au demi-plan solution.

Par conséquent, l'ensemble des solutions de l'inéquation

$-2x+5y\leq 3$ est représenté par la partie du graphique ci-dessous coloriée en vert.

Exercice 6

Soit l'inéquation :

$3y<6-2x$

Vérifions si les couples de nombres réels suivants sont solutions de l'inéquation :

$(0\;;\ -2)\;;\ (0\;;\ 0)\;;\ (1\;;\ 3)\;;\ (4\;;\ 2)$

$(0\;;\ -2)$ est solution de

$3y<6-2x$ si, et seulement si, le couple

$(0\;;\ -2)$ vérifie l'inéquation.

Alors, en remplaçant

$x$ par

$0\$ et

$\ y$ par

$-2$ dans l'inéquation, on obtient :

$3\times(-2)<6-2\times 0$ si, et seulement si,

$-6<6.$ Ce qui est toujours vrai.

Donc, le couple

$(0\;;\ -2)$ est solution de l'inéquation

$3y<6-2x.$

$(0\;;\ 0)$ est solution de

$3y<6-2x$ si, et seulement si, le couple

$(0\;;\ 0)$ vérifie l'inéquation.

Remplaçons alors

$x$ par

$0\$ et

$\ y$ par

$0$ dans l'inéquation

$3y<6-2x.$

On a :

$3\times 0<6-2\times 0$ si, et seulement si,

$3<6.$ Ce qui est toujours vrai.

Par conséquent, le couple

$(0\;;\ 0)$ est solution de l'inéquation

$3y<6-2x.$

$(1\;;\ 3)$ est solution de

$3y<6-2x$ si, et seulement si, le couple

$(1\;;\ 3)$ vérifie l'inéquation.

Alors, en remplaçant

$x$ par

$1\$ et

$\ y$ par

$3$ dans l'inéquation, on obtient :

$3\times 3<6-2\times 1$ si, et seulement si,

$9<4.$ Ce qui est impossible.

D'où, le couple

$(1\;;\ 3)$ n'est pas solution de l'inéquation

$3y<6-2x.$

$(4\;;\ 2)$ est solution de

$3y<6-2x$ si, et seulement si, le couple

$(4\;;\ 2)$ vérifie l'inéquation.

Remplaçons alors

$x$ par

$4\$ et

$\ y$ par

$2$ dans l'inéquation

$3y<6-2x.$

On a :

$3\times 2<6-2\times 4$ si, et seulement si,

$6<-2.$ Ce qui est impossible.

Par conséquent, le couple

$(4\;;\ 2)$ n'est pas solution de l'inéquation

$3y<6-2x.$

Exercice 7

Soit le système d'inéquations suivant :

$\left\lbrace\begin{array}{rcl}3x-2y-9&<&0\\\\-4x&>&-27+3x \end{array}\right.$

Vérifions si les points suivants appartiennent à l'ensemble de solution du système :

$A(3\;;\ 2)\;,\ B(0\;;\ 11)\;,\ C(-4\;;\ 3)\ \text{ et }\ D(-5\;;\ 20)$

En effet, en réécrivant la deuxième inéquation du système, on obtient :

$-4x>-27+3x$ si, et seulement si,

$-4x+27-3x>0$

Ce qui donne :

$-7x+27>0$

Donc, en remplaçant la deuxième inéquation du système par l'inéquation

$-7x+27>0$ , le système devient :

$\left\lbrace\begin{array}{rcl}3x-2y-9&<&0\\\\-7x+27&>&0 \end{array}\right.$

$A$ est solution du système

$\left\lbrace\begin{array}{rcl}3x-2y-9&<&0\\\\-7x+27&>&0 \end{array}\right.$ si, et seulement si, ses coordonnées vérifient chacune des inéquations du système.

Donc, dans la première inéquation, remplaçons

$x$ par

$3\$ et

$\ y$ par

$2.$

On a :

$3\times 3-2\times 2-9<0$ si, et seulement si,

$-4<0.$ Ce qui est toujours vrai.

Donc, les coordonnées

$(3\;;\ 2)$ du point

$A$ vérifient la première inéquation du système.

Dans la deuxième inéquation, en remplaçant

$x$ par

$3$ , on obtient :

$-7\times 3+27>0$ si, et seulement si,

$6>0.$ Ce qui est toujours vrai.

Donc, les coordonnées

$(3\;;\ 2)$ du point

$A$ vérifient la deuxième inéquation du système.

Ainsi, les coordonnées de

$A$ vérifient chacune des inéquations du système.

Par conséquent, le point

$A$ appartient à l'ensemble de solution du système

$\left\lbrace\begin{array}{rcl}3x-2y-9&<&0\\\\-7x+27&>&0 \end{array}\right.$

$B$ est solution du système

$\left\lbrace\begin{array}{rcl}3x-2y-9&<&0\\\\-7x+27&>&0 \end{array}\right.$ si, et seulement si, ses coordonnées vérifient chacune des inéquations du système.

Alors, dans la première inéquation, remplaçons

$x$ par

$0\$ et

$\ y$ par

$11.$

On a :

$3\times 0-2\times 11-9<0$ si, et seulement si,

$-31<0.$ Ce qui est toujours vrai.

Donc, les coordonnées

$(0\;;\ 11)$ du point

$B$ vérifient la première inéquation du système.

Dans la deuxième inéquation, en remplaçant

$x$ par

$0$ , on obtient :

$-7\times 0+27>0$ si, et seulement si,

$27>0.$ Ce qui est toujours vrai.

Donc, les coordonnées

$(0\;;\ 11)$ du point

$B$ vérifient la deuxième inéquation du système.

Ainsi, les coordonnées de

$B$ vérifient chacune des inéquations du système.

D'où, le point

$B$ appartient à l'ensemble de solution du système

$\left\lbrace\begin{array}{rcl}3x-2y-9&<&0\\\\-7x+27&>&0 \end{array}\right.$

$C$ est solution du système

$\left\lbrace\begin{array}{rcl}3x-2y-9&<&0\\\\-7x+27&>&0 \end{array}\right.$ si, et seulement si, ses coordonnées vérifient chacune des inéquations du système.

Donc, dans la première inéquation, remplaçons

$x$ par

$-4\$ et

$\ y$ par

$3.$

On a :

$3\times(-4)-2\times 3-9<0$ si, et seulement si,

$-27<0.$ Ce qui est toujours vrai.

Donc, les coordonnées

$(-4\;;\ 3)$ du point

$C$ vérifient la première inéquation du système.

Dans la deuxième inéquation, en remplaçant

$x$ par

$-4$ , on obtient :

$-7\times(-4)+27>0$ si, et seulement si,

$55>0.$ Ce qui est toujours vrai.

Donc, les coordonnées

$(-4\;;\ 3)$ du point

$C$ vérifient la deuxième inéquation du système.

Ainsi, les coordonnées de

$C$ vérifient chacune des inéquations du système.

Par conséquent, le point

$C$ appartient à l'ensemble de solution du système

$\left\lbrace\begin{array}{rcl}3x-2y-9&<&0\\\\-7x+27&>&0 \end{array}\right.$

$D$ est solution du système

$\left\lbrace\begin{array}{rcl}3x-2y-9&<&0\\\\-7x+27&>&0 \end{array}\right.$ si, et seulement si, ses coordonnées vérifient chacune des inéquations du système.

Donc, dans la première inéquation, remplaçons

$x$ par

$-5\$ et

$\ y$ par

$20.$

On a :

$3\times(-5)-2\times 20-9<0$ si, et seulement si,

$-64<0.$ Ce qui est toujours vrai.

Donc, les coordonnées

$(-5\;;\ 20)$ du point

$D$ vérifient la première inéquation du système.

Dans la deuxième inéquation, en remplaçant

$x$ par

$-5$ , on obtient :

$-7\times(-5)+27>0$ si, et seulement si,

$62>0.$ Ce qui est toujours vrai.

Donc, les coordonnées

$(-5\;;\ 20)$ du point

$D$ vérifient la deuxième inéquation du système.

Ainsi, les coordonnées de

$D$ vérifient chacune des inéquations du système.

D'où, le point

$D$ appartient à l'ensemble de solution du système

$\left\lbrace\begin{array}{rcl}3x-2y-9&<&0\\\\-7x+27&>&0 \end{array}\right.$

Exercice 8

Déterminons une inéquation dont l'ensemble de solutions correspond au demi-plan non hachuré.

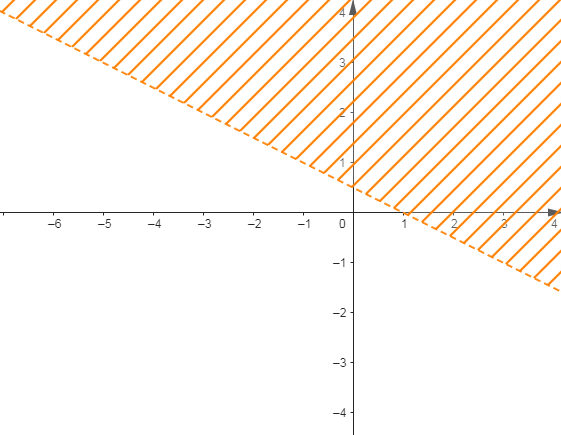
Pour cela, nous allons d'abord déterminer l'équation de la droite

$(D)$ qui partage le plan en deux demi-plans.

En effet, cette droite

$(D)$ est une représentation graphique d'une application affine.

Donc, l'équation de la droite

$(D)$ est de la forme :

$y=ax+b$

avec

$a$ coefficient directeur de la droite

$(D)\$ et

$\ b$ son ordonnée à l'origine.

En observant le graphique, nous remarquons que

$(D)$ passe par les points

$A\left(0\;;\ \dfrac{1}{2}\right)\$ et

$\ B(1\;;\ 0).$

Ainsi, le coefficient directeur

$a$ de

$(D)$ est donné par :

$\begin{array}{rcl} a&=&\dfrac{y_{A}-y_{B}}{x_{A}-x_{B}}\\\\&=&\dfrac{\dfrac{1}{2}-0}{0-1}\\\\&=&\dfrac{\dfrac{1}{2}}{-1}\\\\&=&-\dfrac{1}{2}\end{array}$

Donc,

$a=-\dfrac{1}{2}$

Alors, on a :

$y=-\dfrac{1}{2}x+b$

Comme

$B$ appartient à

$(D)$ alors, en remplaçant les coordonnées de

$B$ dans l'équation de

$(D)$ , on trouve

$b.$

Soit :

$0=-\dfrac{1}{2}\times 1+b$

Ce qui donne :

$b=\dfrac{1}{2}$

Ainsi, l'équation de

$(D)$ est :

$y=-\dfrac{1}{2}x+\dfrac{1}{2}$

Ce qui peut encore s'écrire :

$\boxed{(D)\ :\ 2y+x-1=0}$

Utilisons ensuite un point de vérification appartenant au demi-plan solution pour déterminer l'inéquation.

En observant le graphique, nous remarquons que le point

$O$ appartient à la partie solution mais n'appartient pas à la droite

$(D).$

Donc, remplaçons les coordonnées de

$O$ dans l'équation de

$(D).$

On a :

$2\times 0+0-1=-1<0$

On trouve alors un nombre négatif.

Ce qui signifie que les coordonnées de

$O$ vérifient l'inéquation :

$2y+x-1<0$

Par ailleurs, sur le graphique ci-dessus, on constate que la droite

$(D)$ d'équation

$2y+x-1=0$ n'appartient pas à la solution.

Par conséquent, l'inéquation dont l'ensemble de solutions correspond au demi-plan non hachuré est donnée par :

$2y+x-1<0$

Exercice 9

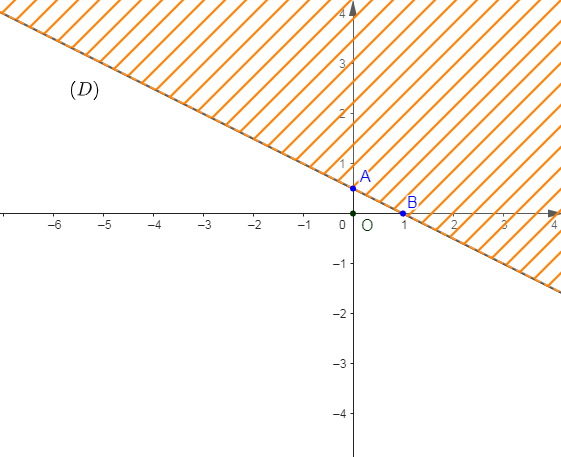
Déterminons un système d'inéquations dont l'ensemble de solutions correspond au demi-plan non hachuré.

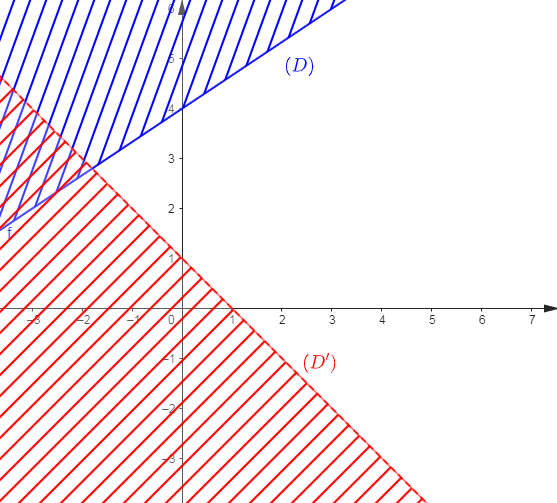
Déterminons d'abord les équations des droites

$(D)\$ et

$\ (D').$

En effet,

$(D)$ est une représentation graphique d'une application affine.

Donc, l'équation de la droite

$(D)$ est de la forme :

$y=ax+b$

avec

$a$ coefficient directeur de la droite

$(D)\$ et

$\ b$ son ordonnée à l'origine.

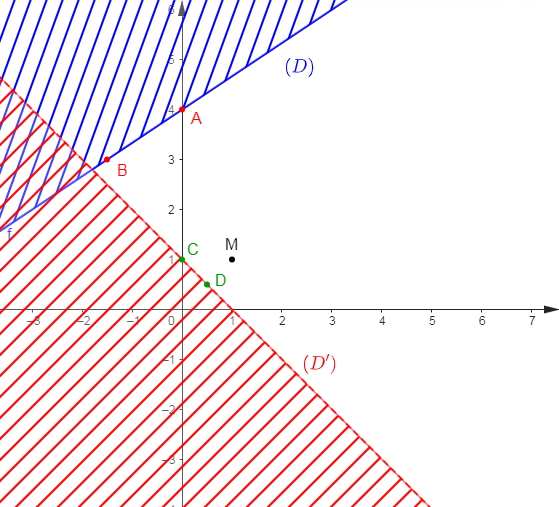
En observant le graphique, nous constatons que

$(D)$ passe par les points

$A(0\;;\ 4)\$ et

$\ B\left(-\dfrac{3}{2}\;;\ 3\right).$

Donc, le coefficient directeur

$a$ de

$(D)$ est donné par :

$\begin{array}{rcl} a&=&\dfrac{y_{A}-y_{B}}{x_{A}-x_{B}}\\\\&=&\dfrac{4-3}{0-\left(-\dfrac{3}{2}\right)}\\\\&=&\dfrac{1}{\dfrac{3}{2}}\\\\&=&\dfrac{2}{3}\end{array}$

Ainsi,

$a=\dfrac{2}{3}$

Alors, on a :

$y=\dfrac{2}{3}x+b$

Comme le point

$A$ est sur la droite

$(D)$ alors, en remplaçant ses coordonnées dans l'équation de

$(D)$ , on trouve

$b.$

Soit :

$4=\dfrac{2}{3}\times 0+b$

Donc,

$b=4$

Ainsi, l'équation de

$(D)$ est :

$y=\dfrac{2}{3}x+4$

Ce qui peut encore s'écrire :

$\boxed{(D)\ :\ 3y-2x-12=0}$

De la même manière, la droite

$(D)$ est de la forme :

$y=ax+b$

Comme

$(D')$ passe par les points

$C(0\;;\ 1)\$ et

$\ D\left(\dfrac{1}{2}\;;\ \dfrac{1}{2}\right)$ alors, le coefficient directeur

$a$ de

$(D)$ est donné par :

$\begin{array}{rcl} a&=&\dfrac{y_{C}-y_{D}}{x_{C}-x_{D}}\\\\&=&\dfrac{1-\dfrac{1}{2}}{0-\dfrac{1}{2}}\\\\&=&\dfrac{\dfrac{1}{2}}{-\dfrac{1}{2}}\\\\&=&-\dfrac{2}{2}\\\\&=&-1\end{array}$

Donc,

$a=-1$

Comme

$C$ appartient à

$(D)$ alors, en remplaçant les coordonnées du point

$C$ dans l'équation de

$(D')$ , on trouve

$b.$

Soit :

$1=-1\times 0+b$

Donc,

$b=1$

Ainsi, l'équation de

$(D')$ est :

$y=-x+1$

Ce qui peut encore s'écrire :

$\boxed{(D')\ :\ y+x-1=0}$

Utilisons ensuite un point de vérification appartenant au demi-plan solution pour déterminer le système d'inéquations.

Considérons alors le point

$M(1\;;\ 1)$ appartient à la partie solution mais n'appartient pas aux droites

$(D)\$ et

$\ (D').$

Remplaçons les coordonnées de

$M$ dans l'équation de

$(D).$

On a :

$3\times 1-2\times 1-12=-11<0$

On trouve alors un nombre négatif.

Ce qui signifie que les coordonnées de

$M$ vérifient l'inéquation :

$3y-2x-12<0$

Par ailleurs, sur le graphique ci-dessus, on constate que la droite

$(D)$ d'équation

$3y-2x-12=0$ appartient à la solution de cette inéquation.

Par conséquent, l'inéquation dont l'ensemble de solutions correspond au demi-plan non hachuré en bleu est donnée par :

$3y-2x-12\leq 0$

De la même manière, en remplaçant les coordonnées de

$M$ dans l'équation de

$(D')$ , on obtient :

$1+1-1=1>0$

On trouve alors un nombre positif.

Ce qui veut dire que les coordonnées de

$M$ vérifient l'inéquation :

$y+x-1>0$

Comme la droite

$(D')$ d'équation

$y+x-1=0$ n'appartient pas à la solution alors, l'inéquation dont l'ensemble de solutions correspond au demi-plan non hachuré en rouge est donnée par :

$y+x-1>0$

Par conséquent, le système d'inéquations dont l'ensemble de solutions correspond au demi-plan non hachuré est donné par :

$\left\lbrace\begin{array}{rcl}3y-2x-12&\leq&0\\\\y+x-1&>&0 \end{array}\right.$

Exercice 10

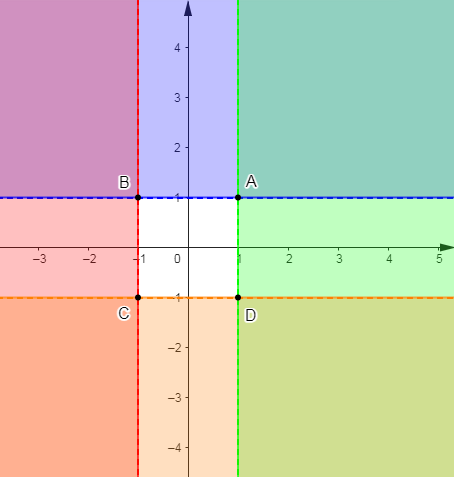
Dans le plan rapporté à un repère orthonormal

$(O\;,\ I\;,\ J)$ , on donne les points :

$A(1\;;\ 1)\;,\ B(-1\;;\ 1)\;,\ C(-1\;;\ -1)\ \text{ et }\ D(1\;;\ -1)$

Trouvons un système d'inéquations dont la solution est formée de l'ensemble des points

$M(x\;;\ y)$ intérieur au carré

$ABCD$

Déterminons d'abord les équations des droites

$(AB)\;,\ (BC)\;,\ (AD)\$ et

$\ (CD).$

En effet, on a :

$(AB)\ :\ y=1$

$(BC)\ :\ x=-1$

$(AD)\ :\ x=1$

$(CD)\ :\ y=-1$

Ce qui peut encore s'écrire :

$(AB)\ :\ y-1=0$

$(BC)\ :\ x+1=0$

$(AD)\ :\ x-1=0$

$(CD)\ :\ y+1=0$

Utilisons ensuite un point de vérification appartenant au demi-plan solution pour déterminer le système d'inéquations.

En observant le graphique, nous remarquons que le point

$O$ appartient à la partie solution mais n'appartient pas aux droites

$(AB)\;,\ (BC)\;,\ (AD)\$ et

$\ (CD).$

Donc, nous choisissons le point

$O$ comme point de vérification.

Remplaçons alors les coordonnées de

$O$ dans l'équation de

$(AB).$

On a :

$0-1=-1<0$

On trouve alors un nombre négatif.

Ce qui signifie que les coordonnées de

$O$ vérifient l'inéquation :

$y-1<0$

Donc, l'inéquation dont l'ensemble de solutions correspond au demi-plan non colorié en bleu est donnée par :

$y-1<0\qquad(1)$

En remplaçant les coordonnées de

$O$ dans l'équation de

$(BC)$ , on trouve :

$0+1=1>0$

On trouve alors un nombre positif.

Ce qui signifie que les coordonnées de

$O$ vérifient l'inéquation :

$x+1>0$

Donc, l'inéquation dont l'ensemble de solutions correspond au demi-plan non colorié en rouge est donnée par :

$x+1>0\qquad(2)$

En remplaçant les coordonnées de

$O$ dans l'équation de

$(AD)$ , on trouve :

$0-1=-1<0$

Ce qui signifie que les coordonnées de

$O$ vérifient l'inéquation :

$x-1<0$

Donc, l'inéquation dont l'ensemble de solutions correspond au demi-plan non colorié en vert est donnée par :

$x-1<0\qquad(3)$

En remplaçant les coordonnées de

$O$ dans l'équation de

$(AD)$ , on trouve :

$0+1=1>0$

Ce qui signifie que les coordonnées de

$O$ vérifient l'inéquation :

$y+1>0$

Donc, l'inéquation dont l'ensemble de solutions correspond au demi-plan non colorié en orange est donnée par :

$y+1>0\qquad(4)$

Par conséquent, le système d'inéquations dont la solution est formée de l'ensemble des points

$M(x\;;\ y)$ intérieur au carré

$ABCD$ est le système formé des inéquations

$(1)\;;\ (2)\;;\ (3)\$ et

$\ (4).$

Ce système est donc donné par :

$\left\lbrace\begin{array}{rcl} y-1&<&0\\\\x+1&>&0\\\\x-1&<&0\\\\y+1&>&0 \end{array}\right.$

Auteur:

Diny Faye

Commentaires

Anonyme (non vérifié)

mar, 03/05/2019 - 11:20

Permalien

Modou et son père ont au

Modou et son père ont au total 50ans.dans 5 ans l'âge de son père sera le triple de son âge. Trouve l'âge de chacun

répondre

mndiaye

mar, 03/05/2019 - 14:27

Permalien

Si x est l'age de Modou et y

Si x est l'age de Modou et y l'age du père, on a x+y=50

Dans 5 ans Modou aura x+5 et le pere y+5 et on aura y+5=3(x+5)

On a un système d'équation à résoudre

x+y=50 (1)

y+5=3(x+5) (2)

(2) donne y+5 =3x+15

y=3x+10

On remplace y par sa valeur sur (1) et on

x+3x+10=50

4x=40

x=10

On remplace x par sa valeur sur (1) on a

10+y=50

y=40

Donc Modou a 10 ans et son père a 40 ans

répondre

Mame Diarra (non vérifié)

mer, 07/01/2020 - 20:58

Permalien

Besoin d'aide

Bonsoir je ne trouve pas la solution de l'exercice 5 J'AI quelques difficultés pour répondre à la 3 ème question

répondre

Oury diallo (non vérifié)

mer, 02/17/2021 - 20:18

Permalien

Réponse aux questions

En aidant les lacunes en maths

répondre

Anonyme (non vérifié)

jeu, 07/30/2020 - 11:14

Permalien

je ne vois pas les autres

je ne vois pas les autres exercices

répondre

Daouda (non vérifié)

dim, 04/04/2021 - 20:58

Permalien

J ai pas vu la suite des

J ai pas vu la suite des exercices

répondre

Moustapha ndiaye (non vérifié)

dim, 06/06/2021 - 14:26

Permalien

Bien je veux vous menvoyer

Bien je veux vous menvoyer des cours francais tout les niveau

répondre

Babacar diop (non vérifié)

dim, 03/13/2022 - 13:10

Permalien

Bonjour je veux resoudre ce

Bonjour je veux resoudre ce systeme {x-2y-4<0 {2x-y+2>0 {-x-2y-4<0

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Solution des exercices : Inéquations et Systèmes d'inéquations à deux inconnues 3e

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 5

Exercice 6

Exercice 7

Exercice 8

Exercice 9

Exercice 10

Commentaires

Ajouter un commentaire

Plain text