Solution des exercices : Proportionnalité - 5e
Classe:
Cinquième
Exercice 1
Avec $3\;L$ de peinture dorée, un peintre a pu décorer $11\;m$ de nappe en papier.
Soit alors $k$ la longueur de nappe en papier, en $m$, que le peintre peut décorer de la même Façon avec $1\;L$ de peinture dorée.
Donc, $k=\dfrac{11}{3}\;m/L$
Déterminons la longueur de nappe en papier, en $m$, que le peintre peut décorer de la même façon avec :
a) $15\;L$ de peinture dorée
Pour passer de $3\;L\ $ à $\ 15\;L$, on multiplie par $5.$
Donc, pour passer de $11\;m$ à la longueur $\ell$ que le peintre peut décorer avec $15\;L$ de peinture dorée, on multiplie aussi par $5.$
D'où, $\ell=5\times 11\;m=55\;m$
b) $0.3\;L$ de peinture dorée
De la même manière, pour passer de $3\;L\ $ à $\ 0.3\;L$, on multiplie par $\dfrac{1}{10}.$
Donc, pour passer de $11\;m$ à la longueur $\ell$ que le peintre peut décorer avec $0.3\;L$ de peinture dorée, on multiplie aussi par $\dfrac{1}{10}.$
Ainsi, $\ell=\dfrac{1}{10}\times 11=\dfrac{11}{10}=1.1\;m$
c) $1\;L$ de peinture dorée
Pour passer de $3\;L\ $ à $\ 1\;L$, on multiplie par $\dfrac{1}{3}.$
Donc, pour passer de $11\;m$ à la longueur $\ell$ que le peintre peut décorer avec $1\;L$ de peinture dorée, on multiplie aussi par $\dfrac{1}{3}.$
Par suite, $\ell=\dfrac{1}{3}\times 11=\dfrac{11}{3}=3.66\;m$
Sous forme de tableau, on obtient :
$$\begin{array}{|l|c|c|c|c|}\hline\text{Peinture dorée }(L)&3&15&0.3&1\\ \hline\text{Longueur nappe }(m)&11&55&1.1&3.66\\ \hline\end{array}$$
Exercice 2
Soit le tableau 1 ci-dessous
Tableau 1
$$\begin{array}{|c|c|c|c|c|}\hline A&12&15&20&25\\ \hline B&16&21&28&35\\ \hline\end{array}$$
$-\ $ Si $A=12\ $ et $\ B=16$ alors, $\dfrac{A}{B}=\dfrac{12}{16}=0.75$
Donc, pour trouver $A$ on multiplie $B$ par $0.75$
$-\ $ Si $A=15\ $ et $\ B=21$ alors, $\dfrac{A}{B}=\dfrac{15}{21}=0.71$
Donc, pour trouver $A$ on multiplie $B$ par $0.71$
Or, $0.75$ est différent de $0.71$ donc, cette situation n'est pas proportionnelle à $B.$
Par conséquent, le tableau 1 ne représente pas une situation de proportionnalité.
Considérons le tableau 2 ci-dessous
Tableau 2
$$\begin{array}{|c|c|c|c|c|}\hline C&1.5&2&2.5&3\\ \hline D&4.5&6&7.5&9\\ \hline\end{array}$$
On a :
$\dfrac{4.5}{1.5}=3$ donc, $4.5=3\times 1.5$
$\dfrac{6}{2}=3$ donc, $6=3\times 2$
$\dfrac{7.5}{2.5}=3$ donc, $7.5=3\times 2.5$
$\dfrac{9}{3}=3$ donc, $9=3\times 3$
On remarque que, pour le passage des valeurs de la première ligne à celles de la deuxième ligne, on multiplie par le même nombre trois $(3).$
Donc, le tableau 2 représente une situation de proportionnalité.
Le coefficient de proportionnalité est $3.$
Exercice 3
Complétons les tableaux de proportionnalité ci-dessous, puis indiquons le coefficient de proportionnalité.
Comme les tableaux $1\ $ et $\ 2$ sont des tableaux de proportionnalité alors, pour le passage des valeurs d'une ligne à celles de l'autre ligne, on multiplie par le même nombre.
Pour le tableau 1, on constate que pour passer de $4\ $ à $\ 4.8$ on multiplie par $1.2$ donc, le coefficient de proportionnalité du tableau 1 est égal à $1.2$
Par suite, pour trouver les autres valeurs de la deuxième ligne, on multiplie chaque valeur de la première ligne par ce même coefficient $1.2$
Soit $b$ la valeur proportionnelle à $7.2$
On a alors : $7.2=1.2\times b$ ce qui donne, $b=\dfrac{7.2}{1.2}=6$
D'où,
Tableau 1
$$\begin{array}{|c|c|c|c|c|}\hline 2&3&4&6&8\\ \hline 2.4&3.6&4.8&7.2&9.6\\ \hline\end{array}$$
Pour le tableau 2, on remarque que pour passer de $4\ $ à $\ 12$ on multiplie par $3$ donc, le coefficient de proportionnalité du tableau 2 est égal à $3.$
Ainsi, pour trouver les autres valeurs de la deuxième ligne, on multiplie chaque valeur de la première ligne par ce même coefficient $3$
D'où,
Tableau 2
$$\begin{array}{|c|c|c|c|c|}\hline 1&3&4&5&7\\ \hline 3&9&12&15&21\\ \hline\end{array}$$
Exercice 4
On considère le tableau de correspondance ci-dessous.
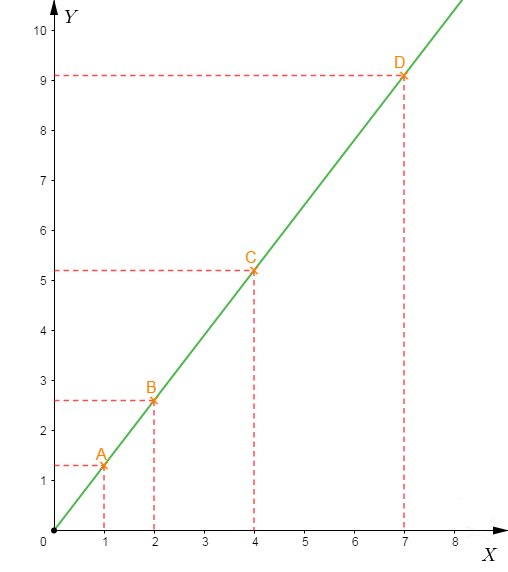
$$\begin{array}{|c|c|c|c|c|}\hline\text{Points} & A & B & C & D \\ \hline X & 1 & 2 & 4 & 7 \\ \hline Y & & 2.6 & & \\ \hline\end{array}$$
1) Complétons ce tableau de proportionnalité.
Comme ce tableau est un tableau de proportionnalité alors, cela signifie que pour le passage des valeurs d'une ligne à celles de l'autre ligne, on multiplie par le même nombre.
On remarque que pour passer de $2\ $ à $\ 2.6$ on multiplie par $1.3$
Donc, pour trouver les autres valeurs de la deuxième ligne, on multiplie chaque valeur de la première ligne par ce même nombre $1.3$
Ce qui donne :
$$\begin{array}{|c|c|c|c|c|}\hline\text{Points}&A&B&C&D \\ \hline X&1&2&4&7 \\ \hline Y&1.3&2.6&5.2&9.1 \\ \hline\end{array}$$
2) Son coefficient de proportionnalité est égal à $1.3$
En effet, pour le passage des valeurs de la première ligne à celles de la deuxième ligne, on multiplie par le même nombre $1.3$
Par conséquent, $1.3$ représente le coefficient de proportionnalité de ce tableau.
3) Représentons graphiquement ce tableau dans un repère.
Pour cela, on place d'abord les points $A\;;\ B\;;\ C\ $ et $\ D$ dans un même repère.
Alors, pour chaque point, la valeur sur la première ligne du tableau représente son abscisse et la valeur sur la deuxième ligne correspond à son ordonnée.
On trace ensuite la droite passant par ces points.
Cette droite caractérise graphiquement ce tableau de proportionnalité.

Exercice 5
On considère le tableau de correspondance ci-dessous.
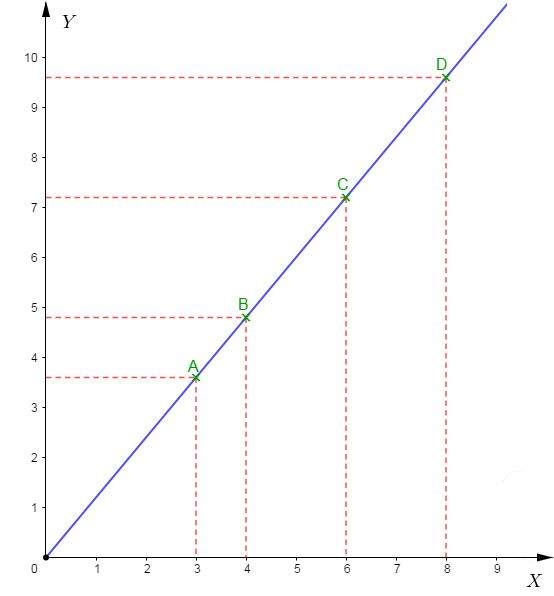
$$\begin{array}{|c|c|c|c|c|}\hline X&3&4&&8 \\ \hline Y&&4.8&7.2& \\ \hline\end{array}$$
1) Complétons ce tableau de proportionnalité.
Comme ce tableau est un tableau de proportionnalité alors, cela signifie que pour le passage des valeurs d'une ligne à celles de l'autre ligne, on multiplie par le même nombre.
On remarque que pour passer de $4\ $ à $\ 4.8$ on multiplie par $1.2$
Donc, pour trouver les autres valeurs de la deuxième ligne, on multiplie chaque valeur de la première ligne par ce même nombre $1.2$
Donc, si $a$ est la valeur proportionnelle à $7.2$, on a :
$$a\times 1.2=7.2$$
Ce qui donne : $a=\dfrac{7.2}{1.2}=6$
On obtient alors le tableau suivant :
$$\begin{array}{|c|c|c|c|c|}\hline X&3&4&6&8 \\ \hline Y&3.6&4.8&7.2&9.6\\ \hline\end{array}$$
2) Son coefficient de proportionnalité est égal à $1.2$
En effet, on constate que pour passer des valeurs de la première ligne à celles de la deuxième ligne, on multiplie par le même nombre $1.2$
Donc, $1.3$ est le coefficient de proportionnalité de ce tableau.
3) Représentons graphiquement ce tableau dans un repère.
Pour cela, on considère quatre points $A\;;\ B\;;\ C\ $ et $\ D.$
Alors, les valeurs sur la première ligne du tableau représentent respectivement les abscisses de ces points et les valeurs sur la deuxième ligne correspondent respectivement aux ordonnées.
On obtient :
$$A(3\;;\ 3.6)\;;\ B(4\;;\ 4.8)\;;\ C(6\;;\ 7.2)\;;\ D(8\;;\ 9.6)$$
On place ensuite ces points dans un même repère.
Enfin, on trace la droite passant par ces points.
Cette droite est la représentation graphique de ce tableau de proportionnalité.

Exercice 7 : "Échelle"
1) La piste de Khouma mesure $1850\;m.$
Déterminons sa longueur en $cm$ sur une carte à l'échelle de $\dfrac{1}{10\,000}$
En effet, on sait que sur une carte ou un plan les dimensions sont égales aux dimensions réelles multipliées par l'échelle.
Donc, si $D$ est la distance réelle, $d$ la distance sur une carte et $e$ l'échelle de cette carte alors, on a :
$$d=D\times e$$
Donc, en remplaçant $D\ $ et $\ e$ par leur valeur, on obtient :
$d=1850\times\dfrac{1}{10\,000}=0.185$
Ainsi, $\boxed{d=0.185\;m=18.5\;cm}$
D'où, longueur de la piste de Khouma sur une carte est égale à $18.5\;cm$
2) Sur une carte, $15\;km$ sont représentés par $6\;cm.$
Déterminons l'échelle $e$ de cette carte.
En effet,, si $D$ distance réelle est représentée sur le plan par $d$ alors, on a :
$$d=D\times e$$
Ce qui donne :
$$e=\dfrac{d}{D}$$
Convertissons d'abord $15\;km$ en $cm.$
On a : $15\;km=1\,500\,000\;cm$
En remplaçant $D\ $ et $\ d$ par leur valeur, on obtient :
$\begin{array}{rcl} e&=&\dfrac{d}{D}\\\\&=&\dfrac{6}{1\,500\,000}\\\\&=&0.000004\end{array}$
Donc, $e=0.000004$
En mettant le nombre décimal $0.000004$ sous forme de fraction décimale, on obtient : $0.000004=\dfrac{4}{1\,000\,000}$
D'où, l'échelle de cette carte est $\boxed{e=\dfrac{4}{1\,000\,000}}$
Exercice 8 : "Pourcentage"
Un hamburger d'une marque américaine pèse $140\;g.$ Il contient $36.40\;g$ de protide, $36.12\;g$ de lipide et $61.32\;g$ de glucide.
1) Déterminons les pourcentages de protides, de lipides et de glucides contenus dans ce hamburger.
$-\ $ Pourcentage de protides
Le pourcentage de protides contenus dans ce hamburger est donné par :
$$\%\text{ protides}=\dfrac{\text{masse de protides}}{\text{masse hamburger}}\times 100$$
En remplaçant, la masse de protides et la masse du hamburger par leur valeur, on obtient :
$\begin{array}{rcl} \%\text{ protides}&=&\dfrac{\text{masse de protides}}{\text{masse hamburger}}\times 100\\\\&=&\dfrac{36.40}{140}\times 100\\\\&=&26\end{array}$
Donc, $\boxed{\%\text{ protides}=26\%}$
Ainsi, ce hamburger contient $26\%$ de protides.
$-\ $ Pourcentage de lipides
Le pourcentage de lipides contenus dans ce hamburger est donné par :
$$\%\text{ protides}=\dfrac{\text{masse de lipides}}{\text{masse hamburger}}\times 100$$
En remplaçant, la masse de lipides et la masse du hamburger par leur valeur, on obtient :
$\begin{array}{rcl} \%\text{ lipides}&=&\dfrac{\text{masse de lipides}}{\text{masse hamburger}}\times 100\\\\&=&\dfrac{36.12}{140}\times 100\\\\&=&25.8\end{array}$
Donc, $\boxed{\%\text{ lipides}=25.8\%}$
D'où, ce hamburger contient $25.8\%$ de lipides.
$-\ $ Pourcentage de glucides
Le pourcentage de glucides contenus dans ce hamburger est donné par :
$$\%\text{ protides}=\dfrac{\text{masse de glucides}}{\text{masse hamburger}}\times 100$$
En remplaçant, la masse de glucides et la masse du hamburger par leur valeur, on obtient :
$\begin{array}{rcl} \%\text{ glucides}&=&\dfrac{\text{masse de protides}}{\text{masse hamburger}}\times 100\\\\&=&\dfrac{61.32}{140}\times 100\\\\&=&43.8\end{array}$
Donc, $\boxed{\%\text{ glucides}=43.8\%}$
Ce qui signifie que ce hamburger contient $43.8\%$ de protides.
2) Le reste (tout ce qui n'est ni protide ni lipides, ni glucides) est de l'eau.
Déterminons le pourcentage d'eau contenu dans ce hamburger.
Comme ce hamburger est constitué de protides, de lipides, de glucides et d'eau alors, on a :
$$\%\text{ protides}+\%\text{ lipides}+\%\text{ glucides}+\%\text{ eau}=100\%$$
Ce qui donne :
$$\%\text{ eau}=100\%-\left(\%\text{ protides}+\%\text{ lipides}+\%\text{ glucides}\right)$$
Ainsi, on a :
$\begin{array}{rcl} \%\text{ eau}&=&100\%-\left(\%\text{ protides}+\%\text{ lipides}+\%\text{ glucides}\right)\\\\&=&100\%-(26\%+25.8\%+43.8\%)\\\\&=&100\%-95.6\%\\\\&=&4.4\%\end{array}$
Donc, $\boxed{\%\text{ eau}=4.4\%}$
D'où, ce hamburger contient $4.4\%$ d'eau.
Exercice 9 : "Vitesse moyenne"
Le tableau ci-dessous représente la distance parcourue en fonction du temps.
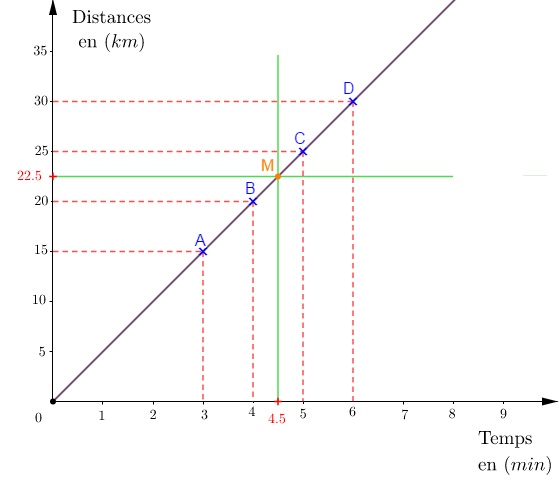
$$\begin{array}{|l|c|c|c|c|}\hline\text{Temps en }(min) & 3 & 4 & 5 & 6 \\ \hline\text{Distances en }(km) & 15 & 20 & 25 & 30 \\ \hline\end{array}$$
1) Montrons que la distance est proportionnelle au temps.
On a :
$\dfrac{15}{3}=5$ donc, $15=5\times 3$
$\dfrac{20}{4}=5$ donc, $20=5\times 4$
$\dfrac{25}{5}=5$ donc, $25=5\times 5$
$\dfrac{30}{6}=5$ donc, $30=5\times 6$
Alors, on remarque que pour le passage des valeurs de la première ligne du tableau à celles de la deuxième ligne, on multiplie par le même nombre cinq $(5).$
Donc, le tableau ci-dessus représente une situation de proportionnalité.
Ce qui signifie que la distance est proportionnelle au temps.
2) Le coefficient de proportionnalité est égal à $5$
En effet, comme la distance est proportionnelle au temps, de coefficient de proportionnalité $5$ alors, on a :
$$\text{Distance parcourue}=5\times \text{Temps}$$
Donc, le coefficient de proportionnalité représente la vitesse moyenne.
3) Représentons graphiquement ce tableau dans un repère orthonormé.
Pour cela, on considère quatre points $A\;;\ B\;;\ C\ $ et $\ D.$
Alors, les valeurs sur la première ligne du tableau représentent respectivement les abscisses de ces points et les valeurs sur la deuxième ligne correspondent respectivement aux ordonnées.
On obtient :
$$A(3\;;\ 15)\;;\ B(4\;;\ 20)\;;\ C(5\;;\ 25)\;;\ D(6\;;\ 30)$$
On place ensuite ces points dans un repère orthonormé.
Traçons enfin la droite qui passe par ces quatre points.
Cette droite est la représentation graphique de ce tableau de proportionnalité.

4) Déterminons graphiquement la distance si le temps de parcourt est de $4.5\;min.$
On place l'abscisse $4.5$ sur l'axe des temps puis, à partir de ce point on trace la droite parallèle à l'axe des distances.
Cette droite coupe la représentation graphique du tableau de proportionnalité au point $M.$
Ensuite, on trace la droite passant par $M$ et qui est parallèle à l'axe des temps.
Cette droite coupe l'axe des distances à hauteur de $22.5$
Cette valeur correspond alors à la distance parcourue pendant $4.5\;min.$
Ainsi, la distance parcourue est égale à $22.5\,km$ si le temps de parcourt est de $4.5\;min$
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
dim, 07/04/2021 - 21:27
Permalien
Pourquoi il donne toute les
Anonyme (non vérifié)
jeu, 03/16/2023 - 14:36
Permalien
Je ne parle pas avec toi
Anonyme (non vérifié)
jeu, 03/16/2023 - 14:36
Permalien
Je ne parle pas avec toi
Anonyme (non vérifié)
mar, 03/14/2023 - 22:53
Permalien
Merci beaucoup vous êtes
Anonyme (non vérifié)
jeu, 03/16/2023 - 14:09
Permalien
Je ne vois pas exercices 6
Anonyme (non vérifié)
jeu, 03/16/2023 - 14:09
Permalien
Je ne vois pas exercices 6
Anonyme (non vérifié)
lun, 06/19/2023 - 23:48
Permalien
Merçi beaucoup
Adji Ndiaye (non vérifié)
dim, 03/17/2024 - 10:52
Permalien
Mathématiques
Anonyme (non vérifié)
mar, 03/19/2024 - 08:15
Permalien
Une personne dort 7h par jour
Halimatou (non vérifié)
dim, 06/02/2024 - 22:59
Permalien
Merci beaucoup pour vos
Ajouter un commentaire