Vous êtes ici

Solution des exercices : Symétrie orthogonale - 6e

Classe:

Sixième

Exercice 1

1) Reproduisons la figure ci-dessous.

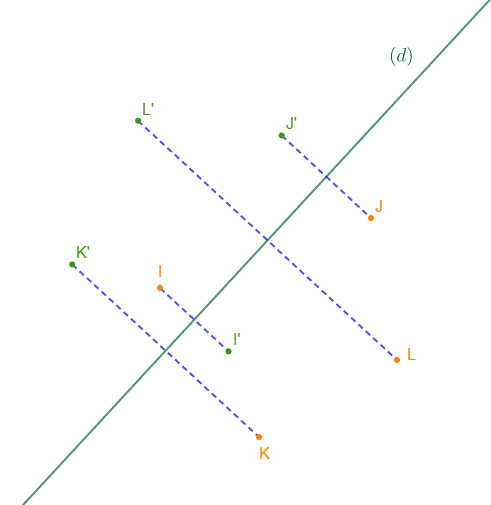
2) Construisons les points

$I'\;,\ J'\;,\ K'\$ et

$\ L'$ symétriques respectifs des points

$I\;,\ J\;,\ K\$ et

$\ L$ par rapport à

$(d).$

Exercice 4

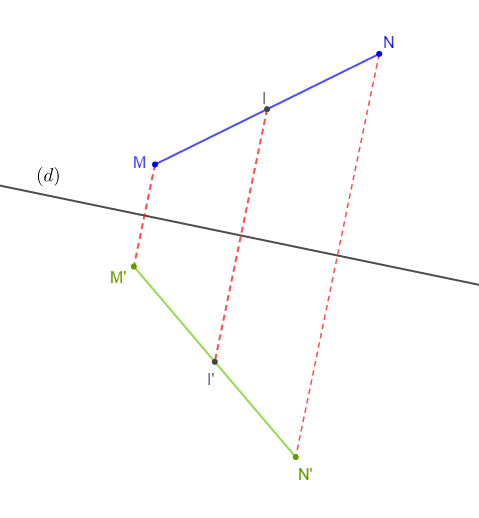
1) Construisons un segment

$[MN]$ oblique tel que :

$MN=5\;cm$ ;

$I$ milieu de

$[MN].$

2) Construisons une droite

$(d)$ extérieur de

$[MN].$

3) Construisons les points

$M'\$ et

$\ N'$ symétriques respectifs de

$M\$ et

$\ N$ par rapport à

$(d).$

4) a) Le symétrique de

$I$ par rapport à

$(d)$ est le point

$I'$ milieu du segment

$[M'N']$

Justifions la réponse.

On sait que l'image du milieu d'un segment par symétrie orthogonale est le milieu de l'image de ce segment.

Or,

$[M'N']$ est le symétrique de

$[MN]$ par rapport à

$(d)\$ et

$\ I$ milieu du segment

$[MN]$ donc, le symétrique de

$I$ par rapport à

$(d)$ est le point

$I'$ mileu de

$[M'N'].$

b) La longueur du segment

$[MN]$ est de

$5\;cm.$

Justifions la réponse.

On sait que

$MN=5\;cm\$ et que

$[M'N']$ est l'image de

$[MN]$ par la symétrie orthogonale d'axe

$(d).$

Or, l'image d'un segment par symétrie orthogonale est un segment de même longueur.

Par conséquent,

$\boxed{M'N'=5\;cm}$

Exercice 5

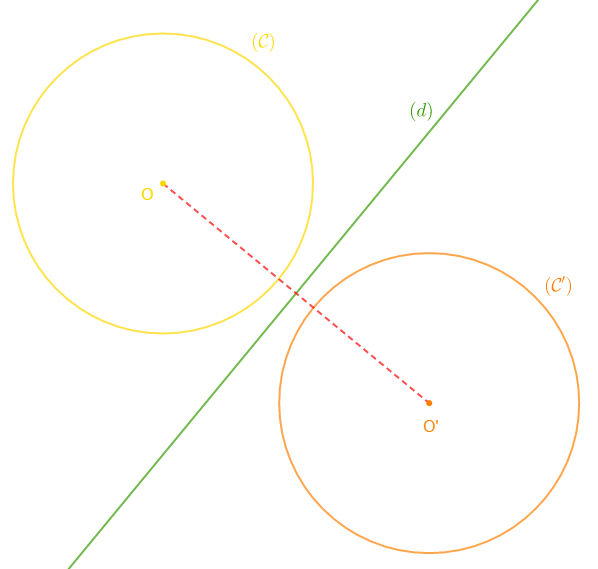
1) Construisons un cercle

$(\mathcal{C})$ de centre

$O$ est de rayon

$3\;cm.$

2) Traçons une droite

$(d)$ extérieur de

$(\mathcal{C}).$

3) Construisons le cercle

$(\mathcal{C}')$ symétrique de

$(\mathcal{C})$ par rapport à

$(d).$

On sait que le symétrique d'un cercle par rapport à un axe est un cercle de même rayon et de centre le symétrique du centre.

Donc,

$(\mathcal{C}')$ est un cercle de même rayon que

$(\mathcal{C})$ et de centre

$O'$ symétrique de

$O$ par rapport à

$(d).$

4) a)

$(\mathcal{C})\$ et

$\ (\mathcal{C}')$ sont disjoints extérieurement.

b) Calculons l'aire du cercle

$(\mathcal{C}').$

Soit

$\mathcal{A}_{(\mathcal{C}')}$ l'aire du cercle

$(\mathcal{C}').$

Alors, on a :

$\mathcal{A}_{(\mathcal{C}')}=\pi\times r'^{2}$ avec

$\pi=3.14\$ et

$\ r'=3\;cm$ ; rayon de

$(\mathcal{C}')$

Donc,

$\begin{array}{rcl}\mathcal{A}_{(\mathcal{C}')}&=&3.14\times 3^{2}\\\\&=&3.14\times 9\\\\&=&28.26\end{array}$

Ainsi,

$\boxed{\mathcal{A}_{(\mathcal{C}')}=28.26\;cm^{2}}$

Exercice 8

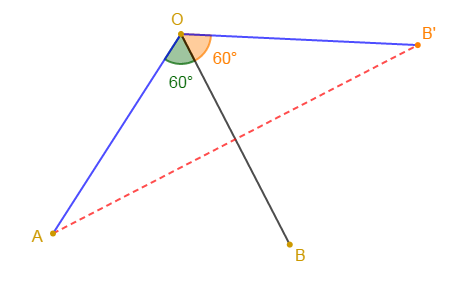
1) Construisons un angle

$AOB$ tel que

$mes\;\widehat{AOB}=60^{\circ}.$

2) Construisons l'angle

$\widehat{B'OB}$ symétrique de l'angle

$\widehat{AOB}$ par rapport à la droite

$(OB).$

L'angle

$\widehat{B'OB}$ est obtenu en construisant les symétriques de

$A\;,\ O\$ et

$\ B$ par rapport à

$(OB).$

Comme

$O\$ et

$\ B$ appartiennent à la droite

$(OB)$ alors, ils sont leur propre symétrique.

Soit

$B'$ le symétrique de

$A$

3) La mesure de l'angle

$\widehat{AOB'}$ est de

$120^{\circ}$

Justifions la réponse.

On sait que l'image d'un angle par symétrie orthogonale est un angle de même mesure donc,

$\widehat{B'OB}=60^{\circ}.$

Comme les angles

$\widehat{AOB}\$ et

$\ \widehat{B'OB}$ sont adjacents alors,

$\widehat{AOB'}=\widehat{AOB}+\widehat{B'OB}.$

Par suite,

$\widehat{AOB'}=60^{\circ}+60^{\circ}=120^{\circ}$

D'où,

$\boxed{\widehat{AOB'}=60^{\circ}}$

Exercice 13

Recopions et complétons les phrases ci-dessous :

1) Si

$A'$ est le symétrique de

$A$ par rapport à une droite

$(D)$ alors

$(D)$ est la médiatrice du segment

$[AA'].$

2) L'axe de symétrie d'une figure est la droite

$(D)$ telle que le symétrique de tout point de la figure est un point de la figure.

3) Deux segments symétriques par rapport à une droite ont la même longueur.

Exercice 14

Reproduisons la figure ci-dessous où

$ABC$ est un triangle tel que

$AH=4\;cm\;,\ BH=2\;cm\$ et

$\ HC=3\;cm.$

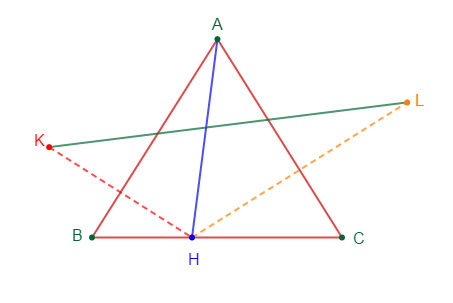
1) Construisons le symétrique

$K$ du point

$H$ par rapport à la droite

$(AB).$

2) Construisons le symétrique

$L$ du point

$H$ par rapport à la droite

$(AC).$

3) Les points

$K\$ et

$\ L$ ne sont pas symétriques par rapport à

$(AH)$

On remarque que la droite

$(AH)$ n'est pas médiatrice du segment

$[KL].$

Par conséquent,

$K\$ et

$\ L$ ne sont pas symétriques par rapport à

$(AH).$

Exercice 15

Parmi les figures ci-dessous, indiquons celle pour laquelle

$A\$ et

$\ A'$ sont symétriques par rapport à la droite

$(L).$ Justifie ta réponse.

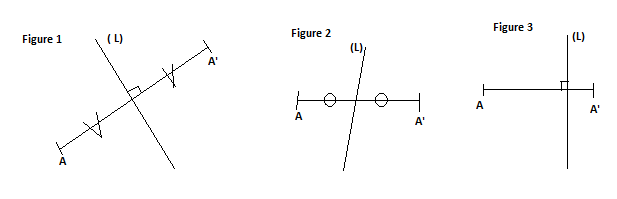
La figure pour laquelle

$A\$ et

$\ A'$ sont symétriques par rapport à la droite

$(L)$ est la figure

$1.$

Justifions la réponse

Sur la figure

$1$ , on constate que la droite

$(L)$ est médiatrice du segment

$[AA'].$ Par conséquent, les points

$A\$ et

$\ A'$ sont symétriques par rapport à cette droite

$(L).$

Par contre, pour la figure

$2$ , on remarque que la droite

$(L)$ passe par le milieu de

$[AA']$ mais n'est pas perpendiculaire. Donc, cette droite n'est pas médiatrice du segment

$[AA'].$ Par conséquent, les points

$A\$ et

$\ A'$ ne sont pas symétriques par rapport à

$(L).$

Aussi, pour la figure

$3$ , la droite

$(L)$ est perpendiculaire à

$(AA')$ mais ne passe pas par le milieu de

$[AA'].$ Donc, cette droite n'est pas médiatrice du segment

$[AA'].$ Par conséquent, les points

$A\$ et

$\ A'$ ne sont pas symétriques par rapport à

$(L).$

Exercice 18

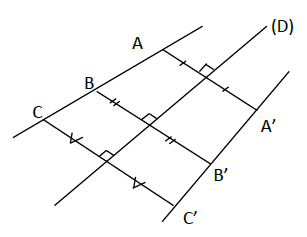
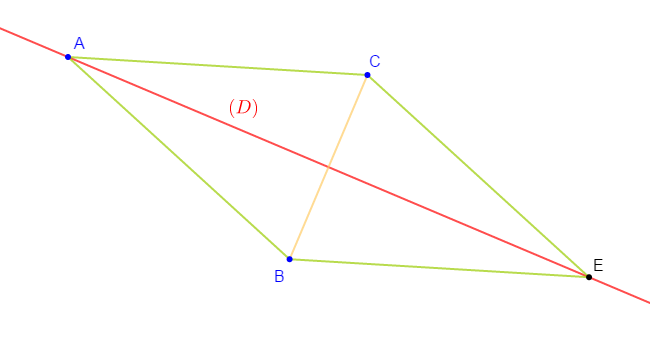
On donne la figure ci-dessous :

1) Les droites

$(AB)\$ et

$\ (B'C')$ sont symétriques par rapport à

$(D).$

On a : la droite

$(B'C')$ passe par les points

$A'\$ et

$\ B'$ qui sont les symétriques respectifs des points

$A\$ et

$\ B$ par rapport à

$(D).$

Donc,

$(AB)\$ et

$\ (B'C')$ sont symétriques par rapport à

$(D).$

2) Les segments

$[AB]\$ et

$\ [B'C']$ ne sont pas symétriques par rapport à

$(D).$

On constate que l'image de

$B$ est

$B'$ mais que

$C'$ n'est pas le symétrique de

$A$ par rapport à

$(D).$

Par conséquent,

$[AB]\$ et

$\ [B'C']$ ne sont pas symétriques par rapport à

$(D).$

3) Les segments

$[AB]\$ et

$\ [B'A']$ sont symétriques par rapport à

$(D).$

On a :

$A'\$ et

$\ B'$ symétriques respectifs des points

$A\$ et

$\ B$ par rapport à

$(D).$

Donc, les segments

$[AB]\$ et

$\ [B'A']$ sont symétriques par rapport à

$(D).$

4) Les demi-droites

$[AB)\$ et

$\ [B'A')$ ne sont pas symétriques par rapport à

$(D).$

On sait que si les deux demi-droites sont symétriques alors, l'image de tout point de

$[AB)$ est sur

$[B'A').$

Or, on a constaté que

$C'$ le symétrique de

$C$ par rapport à

$(D)$ n'appartient pas à la demi-droite

$(B'A').$

Donc, les demi-droites

$[AB)\$ et

$\ [B'A')$ ne sont pas symétriques par rapport à

$(D).$

5) Les demi-droites

$[AB)\$ et

$\ [A'C')$ sont symétriques par rapport à

$(D).$

On constate que le symétrique de tout point de

$[AB)$ appartient à la demi-droite

$[A'C').$

Par conséquent,

$[AB)\$ et

$\ [A'C')$ sont symétriques par rapport à

$(D).$

Exercice 19

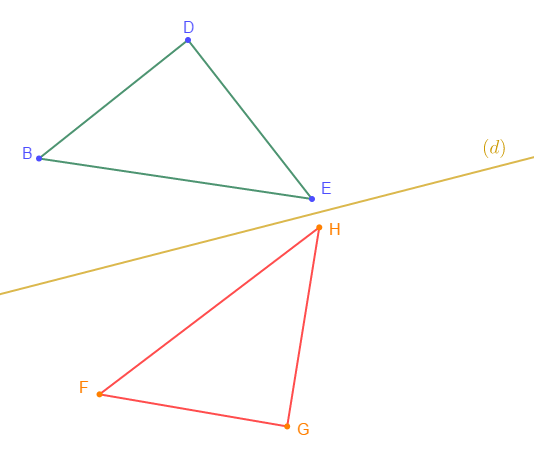
Sur la figure ci-dessous, les deux triangles sont symétriques par rapport

$(d).$

Recopions et complétons les phrases ci-dessous :

1) Le symétrique du point

$D$ par rapport

$(d)$ est le point

$G$ ;

2) Le symétrique du point

$F$ par rapport

$(d)$ est le point

$B$ ;

3) Le symétrique du segment

$[HF]$ par rapport

$(d)$ est le segment

$[EB]$ ;

4) Le symétrique du segment

$[ED]$ par rapport

$(d)$ est le segment

$[HG]$

Exercice 21

1) Construisons un triangle

$ABC$ isocèle en

$A$ tel que

$AB=6\;cm\$ et

$\ BC=4\;cm.$

2) Construisons l'axe de symétrie

$(D)$ de ce triangle.

Comme le triangle

$ABC$ isocèle en

$A$ alors, son axe de symétrie est la médiatrice de

$[BC]$ passant par

$A.$

3) Construisons le point

$E$ symétrique de

$A$ par rapport à

$(BC).$

Justifions que

$E\in(D).$

Comme le point

$E$ est symétrique de

$A$ par rapport à

$(BC)$ alors, la droite

$(BC)$ est médiatrice du segment

$[AE].$

Ce qui signifie que les droites

$(BC)\$ et

$\ (AE)$ sont perpendiculaires.

Or, la droite

$(D)$ passe par

$A$ et est perpendiculaire à la droite

$(BC).$ Donc,

$(D)\$ et

$\ (AE)$ sont confondues.

Par conséquent, le point

$E$ appartient à la droite

$(D).$

$(D)$ représente un axe de symétrie pour le quadrilatère

$ABEC$

$(BC)$ représente un axe de symétrie pour le quadrilatère

$ABEC$

6) Le quadrilatère

$ABEC$ est un losange.

Comme

$(D)\$ et

$\ (AE)$ sont perpendiculaires alors, les diagonales

$[BC]\$ et

$\ [AE]$ du quadrilatère

$ABEC$ sont perpendiculaires.

D'où,

$ABEC$ est un losange.

Auteur:

Diny Faye

Commentaires

Anonyme (non vérifié)

lun, 04/22/2024 - 00:14

Permalien

Pourqoi linda ya pas eso 6et7

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Solution des exercices : Symétrie orthogonale - 6e

Formulaire de recherche

Exercice 1

Exercice 4

Exercice 5

Exercice 8

Exercice 13

Exercice 14

Exercice 15

Exercice 18

Exercice 19

Exercice 21

Commentaires

Pourqoi linda ya pas eso 6et7

Ajouter un commentaire

Plain text