Solution des exercices : Trigonométrie-Ts

Classe: 
Terminale

 Équations trigonométriques

 Exercice 1

1) $\cos\left(2x+\dfrac{\pi}{6}\right)=-\dfrac{1}{2}$
 
L'équation équivaut à $\cos\left(2x+\dfrac{\pi}{6}\right)=\cos\left(\dfrac{2\pi}{3}\right)$, soit à $\left\lbrace\begin{array}{lcl} 2x+\dfrac{\pi}{6}&=&\dfrac{2\pi}{3}+2k\pi\\ \\ 2x+\dfrac{\pi}{6}&=&-\dfrac{2\pi}{3}+2k'\pi\quad\text{ou }(k\;,\ k'\in\mathbb{Z}). \end{array}\right.$
 
La première équation s'écrit après transposition et division par $2$ : 
 
$x=\dfrac{\pi}{4}+k\pi$ et la seconde $x=\dfrac{-5\pi}{12}+k'\pi.$
 
En donnant à $k$ et à $k'$ des valeurs « raisonnables » pour que $x$ et $x'$ restent dans $]-\pi\;,\ \pi]$, on obtient les solutions :
 
$\dfrac{\pi}{4}\;,\ -\dfrac{3\pi}{4}$ (pour $k=0$ et $k=-1$) et $-\dfrac{5\pi}{12}\;,\ \dfrac{7\pi}{4}$, (pour $k'=0$ et $k'=1$).
 
2) $\cos\left(3x-\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}$
 
Démarche analogue au 1). 
 
$S=\left\lbrace-\dfrac{2\pi}{3}\;;\ -\dfrac{\pi}{2}\;;\ 0\;;\ \dfrac{\pi}{6}\;;\ \dfrac{2\pi}{3}\;;\ \dfrac{5\pi}{6}\right\rbrace$
 
3) $\sin\left(x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}$
 
L'équation équivaut à $\sin\left(x+\dfrac{\pi}{3}\right)=\sin\left(\dfrac{\pi}{3}\right)$, soit à $\left\lbrace\begin{array}{lcl} x+\dfrac{\pi}{3}&=&\dfrac{\pi}{3}+2k\pi\\ \\ x+\dfrac{\pi}{3}&=&\pi-\dfrac{\pi}{3}+2k'\pi\quad\text{ou }(k\;,\ k'\in\mathbb{Z}). \end{array}\right.$
 
La première équation s'écrit après transposition : 
 
$x=2k\pi$ et la seconde $x=\dfrac{\pi}{3}+2k'\pi.$
 
En donnant à $k$ et à $k'$ des valeurs « raisonnables » pour que $x$ et $x'$ restent dans $]-\pi\;,\ \pi]$, on obtient :
 
$S=\left\lbrace0\;;\ \dfrac{\pi}{3}\right\rbrace$ (pour $k=0$ et $k'=0$)
 
4) $\sin\left(2x+\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}$
 
Démarche analogue au 2). 
 
$S=\left\lbrace-\dfrac{\pi}{2}\;;\ -\dfrac{\pi}{4}\;;\ \dfrac{\pi}{2}\;;\ \dfrac{3\pi}{4}\right\rbrace$
 
5) $\tan\left(2x-\dfrac{\pi}{4}\right)=-1$
 
L'équation équivaut à $\tan\left(2x-\dfrac{\pi}{4}\right)=\tan\left(-\dfrac{\pi}{4}\right)$, soit à $\left\lbrace\begin{array}{lcl} 2x-\dfrac{\pi}{4}&=&-\dfrac{\pi}{4}+k\pi\quad(k\in\mathbb{Z})\quad(1)\\ \\ 2x-\dfrac{\pi}{4}&\neq &(2h+1)\dfrac{\pi}{2}\;,\quad h\in\mathbb{Z}\quad(2) \end{array}\right.$

ou après résolution à $x=\dfrac{k\pi}{2}\;(k\in\mathbb{Z})$ et $x\neq\dfrac{3\pi}{8}+\dfrac{h\pi}{2}\;,\ h\in\mathbb{Z}.$

 
Dans $]-\pi\;,\ \pi]$, les nombres de la forme $\dfrac{k\pi}{2}$ sont $-\dfrac{\pi}{2}\;;\ 0\;;\ \dfrac{\pi}{2}\;;\ \pi.$
 
On vérifie que :
 
$\ast\ \dfrac{3\pi}{8}+\dfrac{h\pi}{2}=-\dfrac{\pi}{2}\Rightarrow h=-\dfrac{7}{4}$ qui n'est pas entier ;
 
$\ast\ \dfrac{3\pi}{8}+\dfrac{h\pi}{2}=0\Rightarrow h=-\dfrac{3}{4}$ qui n'est pas entier ;
 
$\ast\ \dfrac{3\pi}{8}+\dfrac{h\pi}{2}=\dfrac{\pi}{2}\Rightarrow h=\dfrac{1}{4}$ qui n'est pas entier ;
 
$\ast\ \dfrac{3\pi}{8}+\dfrac{h\pi}{2}=\pi\Rightarrow h=\dfrac{5}{4}$ qui n'est pas entier.
 
On obtient donc comme ensemble de solutions
 
$S=\{-\dfrac{\pi}{2}\;;\ 0\;;\ \dfrac{\pi}{2}\;;\ \pi\}$
 
6) $\tan\left(3x+\dfrac{\pi}{4}\right)=\sqrt{3}$ 
 
L'équation équivaut à $\tan\left(3x+\dfrac{\pi}{4}\right)=\tan\left(\dfrac{\pi}{3}\right)$, soit $\left\lbrace\begin{array}{lcl} 3x+\dfrac{\pi}{4}&=&\dfrac{\pi}{3}+k\pi\quad(k\in\mathbb{Z})\quad(1)\\ \\ 3x+\dfrac{\pi}{4}&\neq &(2h+1)\dfrac{\pi}{2}\;,\quad h\in\mathbb{Z}\quad(2) \end{array}\right.$

ou après résolution à $x=\dfrac{\pi}{36}+\dfrac{k\pi}{3}$ et $x\neq\dfrac{3\pi}{8}+\dfrac{h\pi}{2}.$

 
Dans $]-\pi\;,\ \pi]$, on obtient comme solutions possibles les nombres : 
 
$-\dfrac{35\pi}{36}\;;\ -\dfrac{23\pi}{36}\;;\ -\dfrac{11\pi}{36}\;;\ \dfrac{\pi}{36}\;;\ \dfrac{13\pi}{36}\;;\ \dfrac{25\pi}{36}.$
 
On vérifie que :
 
$\ast$ si $x=-\dfrac{35\pi}{36}$, alors $3x+\dfrac{\pi}{4}=-\dfrac{8\pi}{3}$ qui n'est pas un multiple entier impair de $\dfrac{\pi}{2}$ ;
 
$\ast$ si $x=-\dfrac{23\pi}{36}$, alors $3x+\dfrac{\pi}{4}=-\dfrac{5\pi}{3}$ qui n'est pas un multiple entier impair de $\dfrac{\pi}{2}$ ;
 
$\ast$ si $x=-\dfrac{11\pi}{36}$, alors $3x+\dfrac{\pi}{4}=-\dfrac{2\pi}{3}$ qui n'est pas un multiple entier impair de $\dfrac{\pi}{2}$ ;
 
$\ast$ si $x=\dfrac{\pi}{36}$, alors $3x+\dfrac{\pi}{4}=\dfrac{\pi}{3}$ qui n'est pas un multiple entier impair de $\dfrac{\pi}{2}$ ;
 
$\ast$ si $x=\dfrac{13\pi}{36}$, alors $3x+\dfrac{\pi}{4}=\dfrac{4\pi}{3}$ qui n'est pas un multiple entier impair de $\dfrac{\pi}{2}$ ;
 
$\ast$ si $x=\dfrac{25\pi}{36}$, alors $3x+\dfrac{\pi}{4}=\dfrac{7\pi}{3}$ qui n'est pas un multiple entier impair de $\dfrac{\pi}{2}$ ;
 
Finalement, on a bien : 
 
$S=\left\lbrace-\dfrac{35\pi}{36}\;;\ -\dfrac{23\pi}{36}\;;\ -\dfrac{11\pi}{36}\;;\ \dfrac{\pi}{36}\;;\ \dfrac{13\pi}{36}\;;\ \dfrac{25\pi}{36}\right\rbrace$
 
7) $\cos\left(3x-\dfrac{\pi}{4}\right)=\cos\left(x+\dfrac{\pi}{3}\right)$ 
 
L'équation équivaut au système $\left\lbrace\begin{array}{lcl} 3x-\dfrac{\pi}{4}&=&x+\dfrac{\pi}{3}+2k\pi\\ \text{ou}\\ 3x-\dfrac{\pi}{4}&=&-x-\dfrac{\pi}{3}+2k'\pi \end{array}\right.$

$\quad$
soit après résolution à $\left\lbrace\begin{array}{lcl} x&=&\dfrac{7\pi}{24}+k\pi\\ \text{ou}\\ x&=&\dfrac{\pi}{48}+\dfrac{k'\pi}{4}\end{array}\right.$

Et en choisissant les valeurs de $k$ et $k'$ convenables pour que $x$ appartienne à $]-\pi\;,\ \pi]$, on obtient :

 
$S=\left\lbrace\dfrac{7\pi}{24}\;;\ -\dfrac{17\pi}{24}\;;\ -\dfrac{47\pi}{48}\;;\ -\dfrac{35\pi}{48}\;;\ -\dfrac{23\pi}{48}\;;\ -\dfrac{11\pi}{48}\;;\ \dfrac{\pi}{48}\;;\ \dfrac{13\pi}{48}\;;\ \dfrac{25\pi}{48}\;;\ \dfrac{37\pi}{48}\right\rbrace$
 
8) $\cos\left(2x-\dfrac{\pi}{4}\right)=-\cos\left(3x+\dfrac{\pi}{3}\right)$
 
L'équation équivaut à $\cos\left(2x-\dfrac{\pi}{4}\right)=\cos\left(\pi+\left(3x+\dfrac{\pi}{3}\right)\right)=\cos\left(3x+\dfrac{4\pi}{3}\right)$, soit au système $$\left\lbrace\begin{array}{lcl} 2x-\dfrac{\pi}{4}&=&3x+\dfrac{4\pi}{3}+2k\pi\\ 2x-\dfrac{\pi}{4}&=&-3x-\dfrac{4\pi}{3}+2k'\pi \quad\text{ou }(k\;,\ k'\in\mathbb{Z})\end{array}\right.$$
 
ou encore après résolution à $$\left\lbrace\begin{array}{lcl} x&=&-\dfrac{19\pi}{12}+2k\pi\\ x&=&-\dfrac{13\pi}{60}+\dfrac{2k'\pi}{5} \qquad\text{ou }(k\;,\ k'\in\mathbb{Z})\end{array}\right.$$

Et en donnant à $k$ et $k'$ les valeurs $1$ (pour $k$) et $-1$, $0$, $1$, $2$, $3$ (pour $k'$), on obtient :

 

$S=\left\lbrace\dfrac{5\pi}{12}\;;\ -\dfrac{37\pi}{60}\;;\ -\dfrac{13\pi}{60}\;;\ \dfrac{11\pi}{60}\;;\ \dfrac{35\pi}{60}\;;\ \dfrac{59\pi}{60}\right\rbrace.$
 
9) $\sin\left(x+\dfrac{\pi}{3}\right)=\sin\left(3x-\dfrac{\pi}{6}\right)$
 
L'équation équivaut au système $$\left\lbrace\begin{array}{lcl} x+\dfrac{\pi}{3}&=&3x-\dfrac{\pi}{6}+2k\pi\\  x+\dfrac{\pi}{3}&=&\pi-\left(3x-\dfrac{\pi}{6}\right)+2k'\pi \quad\text{ou }(k\;,\ k'\in\mathbb{Z})\end{array}\right.$$
$\quad$

Soit après résolution à $\left\lbrace\begin{array}{lcl} x&=&\dfrac{\pi}{4}+k\pi\\ x&=&\dfrac{5\pi}{24}+\dfrac{k'\pi}{2} \quad\text{ou }(k\;,\ k'\in\mathbb{Z})\end{array}\right.$

Et en choisissant les valeurs de $k$ et $k'$ convenables pour que $x$ appartienne à $]-\pi\;,\ \pi]$, on obtient :
 

$S=\left\lbrace\dfrac{\pi}{4}\;;\ -\dfrac{3\pi}{4}\;;\ \dfrac{5\pi}{24}\;;\ \dfrac{17\pi}{24}\;;\ -\dfrac{7\pi}{24}\;;\ -\dfrac{19\pi}{24}\right\rbrace.$
 
10) $\sin\left(2x+\dfrac{\pi}{4}\right)=\cos\left(4x-\dfrac{\pi}{3}\right)$
 
L'équation équivaut à $\sin\left(2x+\dfrac{\pi}{4}\right)=\sin\left[\dfrac{\pi}{2}-\left(4x-\dfrac{\pi}{3}\right)\right]$ ou encore à :
 
$\sin\left(2x+\dfrac{\pi}{4}\right)=\sin\left(-4x+\dfrac{5\pi}{6}\right)$, soit au système  $$\left\lbrace\begin{array}{lcl} 2x+\dfrac{\pi}{4}&=&-4x+\dfrac{5\pi}{6}+2k\pi\\  2x+\dfrac{\pi}{4}&=&\pi-\left(-4x+\dfrac{5\pi}{6}\right)+2k'\pi \quad\text{ou }(k\;,\ k'\in\mathbb{Z})\end{array}\right.$$
 
($k$, $k'\in\mathbb{Z}$), ou encore après résolution à $$\left\lbrace\begin{array}{lcl} x&=&\dfrac{7\pi}{72}+\dfrac{k\pi}{3}\\  x&=&\dfrac{\pi}{24}+k'\pi \quad\text{ou }(k\;,\ k'\in\mathbb{Z})\end{array}\right.$$

Et en donnant à $k$ et $k'$ les valeurs $-3$, $-2$, $-1$, $0$, $1$, $2$ (pour $k$) et $-1$, $0$ (pour $k'$), on obtient :

 

$S=\left\lbrace-\dfrac{65\pi}{72}\;;\ -\dfrac{41\pi}{72}\;;\ -\dfrac{17\pi}{72}\;;\ \dfrac{7\pi}{24}\;;\ \dfrac{31\pi}{72}\;;\ \dfrac{55\pi}{72}\;;\ -\dfrac{23\pi}{24}\;;\ \dfrac{\pi}{24}\right\rbrace$
 
11) $\tan\left(x+\dfrac{\pi}{4}\right)=\tan\left(2x-\dfrac{\pi}{4}\right)$ 
 
L'équation équivaut à $\left\lbrace\begin{array}{lcl} x+\dfrac{\pi}{4}&=&2x-\dfrac{\pi}{4}+k\pi\;,\ (k\in\mathbb{Z})\quad(1)\\ \\ x+\dfrac{\pi}{4}&\neq&(2h+1)\dfrac{\pi}{2}\;,\ (h\in\mathbb{Z})\quad(2)\\ \\ 2x-\dfrac{\pi}{4}&\neq&(2l+1)\dfrac{\pi}{2}\;,\ (l\in\mathbb{Z})\quad(3)\\ \end{array}\right.$
$\qquad$
ou après résolution à $\left\lbrace\begin{array}{lcl} x&=&\dfrac{\pi}{2}+k\pi\;,\ (k\in\mathbb{Z})\quad(1)\\ \\ x&\neq&\dfrac{\pi}{4}+h\pi\;,\ (h\in\mathbb{Z})\quad(2)\\ \\ x&\neq&\dfrac{3\pi}{8}+\dfrac{l\pi}{2}\;,\ (l\in\mathbb{Z})\quad(3)\\ \end{array}\right.$
 
Dans $]-\pi\;,\ \pi]$, on obtient comme solutions possibles de (1) les nombres : $\dfrac{\pi}{2}$ et $\dfrac{3\pi}{2}.$ 
 
On vérifie que :
 
$\ast\ \dfrac{\pi}{4}+h\pi=\dfrac{\pi}{2}\Rightarrow h=\dfrac{1}{4}$ qui n'est pas un entier non plus.
 
$\ast\ \dfrac{3\pi}{8}+\dfrac{l\pi}{2}=\dfrac{\pi}{2}\Rightarrow l=\dfrac{1}{4}$ qui n'est pas un entier et $\dfrac{3\pi}{8}+\dfrac{l\pi}{2}=\dfrac{3\pi}{2}\Rightarrow l=\dfrac{9}{4}$ qui n'est pas un entier non plus.
 
L'ensemble des solutions de cette équation est donc bel et bien $S=\left\lbrace\dfrac{\pi}{2}\;;\ \dfrac{3\pi}{2}\right\rbrace.$ 
 
12) $\tan\left(2x+\dfrac{\pi}{3}\right)=-co\tan\left(3x-\dfrac{\pi}{4}\right)$
 
L'équation équivaut, d'après les formules, successivement aux équations suivantes :
 
$\tan\left(2x+\dfrac{\pi}{3}\right)=co\tan\left(-3x+\dfrac{\pi}{4}\right)$, $\tan\left(2x+\dfrac{\pi}{3}\right)=\tan\left[\dfrac{\pi}{2}-\left(-3x+\dfrac{\pi}{4}\right)\right]$ et $\tan\left(2x+\dfrac{\pi}{3}\right)=\tan\left(3x+\dfrac{\pi}{4}\right)$, ce qui entraîne $2x+\dfrac{\pi}{3}=3x+\dfrac{\pi}{4}+k\pi\;,\ (k\in\mathbb{Z})$ ou après résolution :
 
$x=\dfrac{\pi}{12}+k\pi\;,\ (k\in\mathbb{Z}).$
 
Dans $]-\pi\;,\ \pi]$, on obtient comme solutions possibles les nombres $\dfrac{\pi}{12}$ et $-\dfrac{11\pi}{12}.$
 
$\ast$ Si $x=-\dfrac{11\pi}{12}$, alors $2x+\dfrac{\pi}{3}=-\dfrac{3\pi}{2}$ qui est un multiple entier impair de $\dfrac{\pi}{2}$ ;
 
$\ast$ Si $x=\dfrac{\pi}{12}$, alors $2x+\dfrac{\pi}{3}=\dfrac{\pi}{2}$ qui est un multiple entier impair de $\dfrac{\pi}{2}.$
 
Ces valeurs ne conviennent donc pas comme solutions de l'équation et par conséquent : $S=\varnothing$

Exercice 2

1) $4\cos^{2}x-1=0$
 
L'équation équivaut à la réunion des deux équations :
 
$\cos x=\dfrac{1}{2}\text{ ou }\cos x=-\dfrac{1}{2}.$
 
$S=\left\lbrace\dfrac{\pi}{3}\;;\ -\dfrac{\pi}{3}\;;\ \dfrac{2\pi}{3}\;;\ -\dfrac{2\pi}{3}\right\rbrace$
 
2) $4\cos^{2}\left(x+\dfrac{\pi}{3}\right)-3=0$ 
 
L'équation équivaut à la réunion des deux équations : 
 
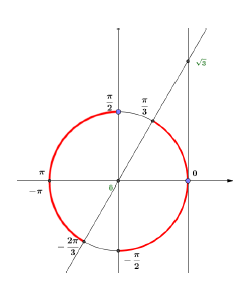
$\cos\left(x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\text{ ou encore à }\cos\left(x+\dfrac{\pi}{3}\right)=\cos\left(\dfrac{\pi}{6}\right)\text{ ou bien }\cos\left(x+\dfrac{\pi}{3}\right)=\cos\left(\pi-\dfrac{\pi}{6}\right)=\cos\left(\dfrac{5\pi}{6}\right).$
 
On obtient les systèmes : 
 
$$(I)\ \left\lbrace\begin{array}{lcl} x+\dfrac{\pi}{3}&=&\dfrac{\pi}{6}+2k\pi\\ \\ x+\dfrac{\pi}{3}&=&-\dfrac{\pi}{6}+2k'\pi\quad(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$$
$\quad$
$$\text{Et}\quad(II)\ \left\lbrace\begin{array}{lcl} x+\dfrac{\pi}{3}&=&\dfrac{5\pi}{6}+2k\pi\\ \\ x+\dfrac{\pi}{3}&=&-\dfrac{5\pi}{6}+2k'\pi\quad(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$$
$\quad$
$$\text{soit, après résolution à :}\quad(I)\ \left\lbrace\begin{array}{lcl} x&=&-\dfrac{\pi}{6}+2k\pi\\ \\ x&=&-\dfrac{\pi}{2}+2k'\pi\quad(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$$
$\quad$
$$\text{Et}\quad(II)\ \left\lbrace\begin{array}{lcl} x&=&\dfrac{\pi}{2}+2k\pi\\ \\ x&=&-\dfrac{7\pi}{6}+2k'\pi\quad(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$$
 
$S=\left\lbrace-\dfrac{\pi}{12}\;;\ -\dfrac{\pi}{2}\;;\ \dfrac{\pi}{2}\;;\ \dfrac{5\pi}{6}\right\rbrace$
 
($k=0$ et $k'=0$ pour le système (I)), ($k=0$ et $k'=1$ pour le système (II)).
 
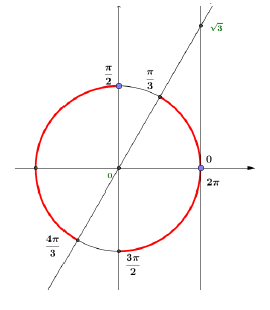
3) $2\sin^{2}\left(2x+\dfrac{\pi}{3}\right)-1=0$
 
L'équation équivaut à la réunion des deux équations : 
 
$\sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{1}{\sqrt{2}}$ ou $\sin\left(2x+\dfrac{\pi}{3}\right)=-\dfrac{1}{\sqrt{2}}$ ou encore à $\sin\left(2x+\dfrac{\pi}{3}\right)=\sin\left(\dfrac{\pi}{4}\right)$ ou bien $\sin\left(2x+\dfrac{\pi}{3}\right)=-\sin\left(\dfrac{\pi}{4}\right)=\sin\left(-\dfrac{\pi}{4}\right).$ 
 
On obtient les systèmes :
 
$$(I)\ \left\lbrace\begin{array}{lcl} 2x+\dfrac{\pi}{3}&=&\dfrac{\pi}{4}+2k\pi\\ \\ 2x+\dfrac{\pi}{3}&=&\dfrac{3\pi}{4}+2k'\pi\quad(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$$
$\quad$
$$\text{Et}\quad(II)\ \left\lbrace\begin{array}{lcl} 2x+\dfrac{\pi}{3}&=&-\dfrac{\pi}{4}+2k\pi\\ \\ 2x+\dfrac{\pi}{3}&=&\dfrac{5\pi}{4}+2k'\pi\quad(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$$
$\quad$
$$\text{soit, après résolution à :}\quad(I)\ \left\lbrace\begin{array}{lcl} x&=&-\dfrac{\pi}{24}+2k\pi\\ \\ x&=&\dfrac{5\pi}{24}+2k'\pi\quad(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$$
$\quad$
$$\text{Et}\quad(II)\ \left\lbrace\begin{array}{lcl} x&=&-\dfrac{7\pi}{24}+2k\pi\\ \\ x&=&\dfrac{11\pi}{24}+2k'\pi\quad(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$$
 
$S=\left\lbrace-\dfrac{\pi}{24}\;;\ \dfrac{23\pi}{24}\;;\ \dfrac{5\pi}{24}\;;\ -\dfrac{19\pi}{24}\;;\ -\dfrac{7\pi}{24}\;;\ \dfrac{19\pi}{24}\;;\ \dfrac{11\pi}{24}\;;\ -\dfrac{13\pi}{24}\right\rbrace$
 
($k=0$, $k=1$ et $k'=0$, $k'=-1$ pour le système (I)), ($k=0$, $k=1$ et $k'=0$, $k'=-1$ pour le système (II)).
 
4) $2\sin x\cos x+\sqrt{3}\cos 2x=0$
 
L'équation s'écrit $\sin 2x+\sqrt{3}\cos 2x=0$ en utilisant la formule $\sin 2x=2\sin x\cos x.$
 
On reconnait là une équation du type $a\cos u+b\sin u=c.$
 
Pour se ramener à une équation trigonométrique usuelle, il faut diviser les deux membres par $\sqrt{a^{2}+b^{2}}.$ 
 
Ainsi l'équation proposée devient : $\dfrac{1}{2}\sin 2x+\dfrac{\sqrt{3}}{2}\cos 2x=0$, soit d'après une formule d'addition :
 
$\sin\dfrac{\pi}{6}\sin 2x+\cos\dfrac{\pi}{6}\cos 2x=0\Leftrightarrow\cos\left(\dfrac{\pi}{6}-2x\right)=0=\cos\left(\dfrac{\pi}{2}\right).$ 
 
La résolution de cette dernière équation conduit au système : $\left\lbrace\begin{array}{lcl} \dfrac{\pi}{6}-2x&=&\dfrac{\pi}{2}+2k\pi\text{ ou}\\ \\ \dfrac{\pi}{6}-2x&=&-\dfrac{\pi}{2}+2k'\pi\quad(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$ 
 
soit après résolution à $\left\lbrace\begin{array}{lcl} x&=&-\dfrac{\pi}{6}+k\pi\\ \\ x&=&\dfrac{\pi}{3}+k'\pi\quad(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$  
 
Dans $]-\pi\;,\ \pi]$, on obtient les solutions $-\dfrac{\pi}{6}$, $\dfrac{5\pi}{6}$, $\dfrac{\pi}{3}$ et $-\dfrac{2\pi}{3}.$
 
5) $\tan^{2}\left(3x+\dfrac{\pi}{6}\right)-1=0$
 
L'équation équivaut à la réunion des deux équations : 
 
$\tan\left(3x+\dfrac{\pi}{6}\right)=1$ ou $\tan\left(3x+\dfrac{\pi}{6}\right)=-1$ dont la résolution, laissée au lecteur, conduit aux solutions du type : 
 
$x=\dfrac{\pi}{36}+\dfrac{k\pi}{3}$ ou $x=\dfrac{-5\pi}{36}+\dfrac{k'\pi}{3}$, $(k\;,\ k'\in\mathbb{Z}).$ 
 
Dans $]-\pi\;,\ \pi]$, on obtient les six solutions $\dfrac{\pi}{36}$, $\dfrac{13\pi}{36}$, $\dfrac{25\pi}{36}$, $-\dfrac{11\pi}{36}$, $-\dfrac{23\pi}{36}$, $-\dfrac{35\pi}{36}$ pour le premier type (correspondant aux valeurs respectives $0$, $1$, $2$, $-1$, $-2$, $-3$ de $k)$ et les six solutions $-\dfrac{5\pi}{36}$, $\dfrac{7\pi}{36}$, $\dfrac{19\pi}{36}$, $\dfrac{31\pi}{36}$,  $-\dfrac{17\pi}{36}$, $-\dfrac{29\pi}{36}$ pour le deuxième type (correspondant aux valeurs respectives $0$, $1$, $2$, $3$, $-1$, $-2$ de $k')$. 
 
On vérifie que pour chacune de ces solutions $\alpha$, on a
$$3\alpha+\dfrac{\pi}{6}\neq(2h+1)\dfrac{\pi}{2}\;,\ h\in\mathbb{Z}$$, en d'autres termes que l'équation est bien définie pour chacune d'elles.
 
Cette équation admet donc en tout $12$ solutions dans $]-\pi\;,\ \pi].$
 
6) $\tan^{2}\left(2x-\dfrac{\pi}{4}\right)-3=0$
 
Cette équation est tout à fait analogue à la précédente. 
 
Nous nous bornons à en donner l'ensemble des solutions. 
 
$S=\left\lbrace\dfrac{\pi}{3}\;;\ \dfrac{5\pi}{6}\;;\ -\dfrac{\pi}{6}\;;\ -\dfrac{2\pi}{3}\;;\ 0\;;\ \dfrac{\pi}{2}\;;\ \pi\;;\ -\dfrac{\pi}{2}\right\rbrace.$ 
 
On vérifie que l'équation
$$2x-\dfrac{\pi}{4}=(2h+1)\dfrac{\pi}{2}\;;\ h\in\mathbb{Z}.$$, a pour solutions les nombres de la forme $\dfrac{3\pi}{8}+\dfrac{h\pi}{2}.$ 
 
Ceux que ces derniers qui appartiennent à $]-\pi\;,\ \pi]$ sont : 
 
$S=\dfrac{3\pi}{8}\;;\ \dfrac{7\pi}{8}\;;\ -\dfrac{\pi}{8}\;;\ -\dfrac{5\pi}{8}.$  
 
Aucun d'eux n'est dans $S.$
 
7) $\tan^{2}\left(x+\dfrac{\pi}{4}\right)=\tan^{2}(2x)$
 
L'équation équivaut à $\left\lbrace\left(\tan\left(x+\dfrac{\pi}{4}\right)=\tan(2x)\right)\text{ ou }\left(\tan\left(x+\dfrac{\pi}{4}\right)=-\tan(2x)\right)\right\rbrace$, ce qui conduit à l'une des deux équations :
 
$x+\dfrac{\pi}{4}=2x+k\pi\ (k\in\mathbb{Z}\quad(1)\text{ ou }x+\dfrac{\pi}{4}=-2x+k'\pi\ (k'\in\mathbb{Z}\quad(2).$
 
La première d'entre elles a pour solutions les nombres de la forme $x=\dfrac{\pi}{4}+k\pi$ et la seconde les nombres de la forme $x=-\dfrac{\pi}{12}+\dfrac{k'\pi}{3}.$
 
On obtient donc a priori comme solutions possibles les nombres :
 
$-\dfrac{3\pi}{4}\;;\ \dfrac{\pi}{4}$ obtenus respectivement pour $k=-1$, $k=0$, et $-\dfrac{3\pi}{4}\;;\ -\dfrac{5\pi}{12}\;;\ -\dfrac{\pi}{12}\;;\ \dfrac{\pi}{4}\;;\ \dfrac{7\pi}{12}\;;\ \dfrac{11\pi}{12}$ obtenus respectivement pour $k'=-2$, $k'=-1$, $k'=0$, $k'=1$, $k'=2$ et $k'=3.$
 
Il faut maintenant vérifier que pour chacune de ces valeurs, les expressions $x+\dfrac{\pi}{4}$ ne sont pas des multiples impairs de $\dfrac{\pi}{2}.$
 
Or
 
$\ast$ si $x=-\dfrac{3\pi}{4}$, alors $2x=-\dfrac{3\pi}{2}$ qui est un multiple impair de $\dfrac{\pi}{2}$ ;
 
$\ast$ si $x=\dfrac{\pi}{4}$, alors $2x=\dfrac{\pi}{2}$ qui est un multiple impair de $\dfrac{\pi}{2}$ ;
 
$\ast$ si $x=-\dfrac{5\pi}{12}$, alors $2x=-\dfrac{5\pi}{6}$ et $x+\dfrac{\pi}{4}=-\dfrac{7\pi}{12}$ et aucun de ces deux nombres n'est un multiple impair de $\dfrac{\pi}{2}$ ;
 
$\ast$ si $x=-\dfrac{\pi}{12}$, alors $2x=-\dfrac{\pi}{6}$ et $x+\dfrac{\pi}{4}=\dfrac{\pi}{6}$ et aucun de ces deux nombres n'est un multiple impair de $\dfrac{\pi}{2}$ ;
 
$\ast$ si $x=\dfrac{7\pi}{12}$, alors $2x=\dfrac{7\pi}{6}$ et $x+\dfrac{\pi}{4}=\dfrac{5\pi}{6}$ et aucun de ces deux nombres n'est un multiple impair de $\dfrac{\pi}{2}$ ;
 
$\ast$ Enfin si $x=\dfrac{11\pi}{12}$, alors $2x=\dfrac{11\pi}{6}$ et $x+\dfrac{\pi}{4}=\dfrac{7\pi}{6}$ et aucun de ces deux nombres n'est un multiple impair de $\dfrac{\pi}{2}.$
 
 
En conclusion, on peut retenir toutes les valeurs trouvées, sauf $-\dfrac{3\pi}{4}$ et $\dfrac{\pi}{4}.$
 
$S=\left\lbrace-\dfrac{5\pi}{12}\;;\ -\dfrac{\pi}{12}\;;\ \dfrac{7\pi}{12}\;;\ \dfrac{11\pi}{12}\right\rbrace$
 
8) $\tan\left(x+\dfrac{\pi}{3}\right)=\sin\left(x+\dfrac{\pi}{3}\right)$ 
 
L'équation est définie si $x+\dfrac{\pi}{3}$ n'est pas un multiple impair de $\dfrac{\pi}{2}$, en d'autres termes si
$$x+\dfrac{\pi}{3}\neq(2h+1)\dfrac{\pi}{2}\;,\ h\in\mathbb{Z}.$$
 
Or l'égalité $x+\dfrac{\pi}{3}=(2h+1)\dfrac{\pi}{2}$ équivaut à : $x=\dfrac{\pi}{6}+h\pi.$
 
Les nombres de cette dernière forme devront donc être exclus de l'ensemble des solutions.
 
Cela étant, l'équation s'écrit : $\dfrac{\sin\left(x+\dfrac{\pi}{3}\right)}{\cos\left(x+\dfrac{\pi}{3}\right)}=\sin\left(x+\dfrac{\pi}{3}\right)\Leftrightarrow\sin\left(x+\dfrac{\pi}{3}\right)\left[\dfrac{1}{\cos\left(x+\dfrac{\pi}{3}\right)}-1\right]=0.$
 
Cette dernière égalité signifie que l'on a soit $\sin\left(x+\dfrac{\pi}{3}\right)=0\quad(1)$

ou bien $\cos\left(x+\dfrac{\pi}{3}\right)=1\quad(2)$ avec $x\neq\dfrac{\pi}{6}+h\pi\;,\ h\in\mathbb{Z}.$

 
L'équation (1) équivaut à $x+\dfrac{\pi}{3}=k\pi$ et a pour solutions dans $\mathbb{R}$ les nombres de la forme
$$x=-\dfrac{\pi}{3}+k\pi$$
 
L'équation (2) équivaut à $x+\dfrac{\pi}{3}=2k\pi$ et a pour solutions dans $\mathbb{R}$ les nombres de la forme
$$x=-\dfrac{\pi}{3}+2k\pi$$
 
On vérifie que les nombres de l'un de ces deux types qui appartiennent à $]-\pi\;,\ ]$ sont $-\dfrac{\pi}{3}$ et $\dfrac{3\pi}{3}.$
 
Aucun d'eux n'est de la forme $\dfrac{\pi}{6}+h\pi\;,\ h\in\mathbb{Z}.$
 
En effet, l'égalité $-\dfrac{\pi}{3}=\dfrac{\pi}{6}+h\pi$ entraîne, en simplifiant par $\pi$, que $h=-\dfrac{1}{3}-\dfrac{1}{6}=-\dfrac{1}{2}$, ce qui est impossible, puisque $h$ est entier et de même l'égalité $\dfrac{2\pi}{3}=\dfrac{\pi}{6}+h\pi$ entraîne $h=\dfrac{2}{3}-\dfrac{1}{6}=\dfrac{1}{2}.$
 
Finalement, on conclut que $S=\left\lbrace-\dfrac{\pi}{3}\;;\ \dfrac{2\pi}{3}\right\rbrace.$ 

Exercice 3

1) $2\cos^{2}x+\left(\sqrt{3}+2\right)\cos x+\sqrt{3}=0.$ 
 
L'équation devient, après le changement de variable $X=\cos x$,
$$2X^{2}+\left(\sqrt{3}+2\right)X+\sqrt{3}=0$$, équation du second degré qui a pour racines $-\dfrac{1}{2}$ et $-1.$
 
L'équation équivaut donc à :
 
$\cos x=-\dfrac{1}{2}$ ou $\cos x=-1.$
 
On obtient, dans $[0\;;\ 2\pi[$ les solutions : $\dfrac{2\pi}{3}\;,\ \pi\text{ et }\dfrac{4\pi}{3}.$
 
 
 
2) $\cos 2x=3\cos x-2.$
 
On remplace d'abord cos $2x$ par $2\cos^{2}x-1.$
 
L'équation devient alors 
$$2\cos^{2}x-3\cos x+1=0$$ 
 
Le changement de variable $X=\cos x$ ramène l'équation de départ à l'équation du second degré
$$2X^{2}-3X+1=0$$, qui a pour racines $1$ et $\dfrac{1}{2}.$
 
L'équation équivaut donc à : $\cos c=1$ ou $\cos x=\dfrac{1}{2}.$ 
 
On obtient dans $[0\;;\ 2\pi[$ les solutions : $0$, $\dfrac{\pi}{3}$ et $\dfrac{5\pi}{3}.$
 
 
 
3) $1+\cos 2x+\cos 4x=0$
 
La formule de l'angle double relative au cosinus entraîne que $\cos 4x=2\cos^{2} 2x-1$ puis en effectuant le changement de variable $X=\cos 2x$, on ramène l'équation de départ à l'équation du second degré $1+X+2X^{2}-1=0$, soit après réduction : $2X^{2}+X=0.$ 
 
Cette dernière équation a pour solutions $X=0$ et $X=-\dfrac{1}{2}$, en d'autres termes elle équivaut à $$\cos 2x=0\text{ ou }\cos 2x=-\dfrac{1}{2}.$$
 
$\ast\ \cos 2x=0\Leftrightarrow 2x=2k\pi\Leftrightarrow x=k\pi\ (k\in\mathbb{Z}).$ 
 
Dans $[0\;;\ 2\pi[$, on obtient les solutions : $0$ et $\pi$ pour les valeurs respectives $0$ et $1$ de $k.$
 
$\ast\ \cos 2x=-\dfrac{1}{2}\Leftrightarrow\left\lbrace\begin{array}{lcl} 2x&=&\dfrac{2\pi}{3}+2k_{1}\pi\\ \\ 2x&=&-\dfrac{2\pi}{3}+2k'_{1}\pi\text{ ou }(k_{1}\;,\ k'_{1}\in\mathbb{Z}) \end{array}\right.$

soit $\left\lbrace\begin{array}{lcl} x&=&\dfrac{\pi}{3}+k_{1}\pi\\ \\ x&=&-\dfrac{\pi}{3}+k'_{1}\pi\quad\text{ou }(k_{1}\;,\ k'_{1}\in\mathbb{Z}) \end{array}\right.$

 
Dans $[0\;;\ 2\pi[$, on obtient les solutions : $\dfrac{\pi}{3}$, $\dfrac{4\pi}{3}$ pour les valeurs respectives $0$ et $1$ de $k_{1}$ et $\dfrac{2\pi}{3}$, $\dfrac{5\pi}{3}$ pour les valeurs respectives $1$ et $2$ de $k'_{1}.$
 
En résumé, $S=\left\lbrace 0\;;\ \pi\;;\ \dfrac{\pi}{3}\;;\ \dfrac{4\pi}{3}\;;\ \dfrac{2\pi}{3}\;;\ \dfrac{5\pi}{3}\right\rbrace$ 
 
4) $2\cos x+\cos 3x+\cos 5x=0$
 
D'après la formule de factorisation $\cos p+\cos q=2\cos\dfrac{p+q}{2}\cos\dfrac{p-q}{2}$, on peut écrire :
$$\cos 3x+\cos 5x=2\cos 4x\cos x$$
 
En substituant les deux derniers termes de l'équation par le membre de droite de cette dernière égalité, on obtient $2\cos x+2\cos 4x\cos x=0$, soit $2\cos x(\cos 4x+1)=0.$
 
L'équation équivaut par conséquent à $\cos x=0$ ou $\cos 4x=-1.$
 
$\ast\ \cos x=0\Leftrightarrow x=2k\pi\ (k\in\mathbb{Z})$
 
$\ast\ \cos 4x=-1\Leftrightarrow 4x=\pi+2k_{1}\pi\ (k_{1}\in\mathbb{Z})\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k_{1}\pi}{2}.$
 
En donnant à $k$ et $k_{1}$ des valeurs convenables, on trouve comme ensemble de solutions dans $[0\;;\ 2\pi[$ :
 
$S=\left\lbrace 0\;;\ \dfrac{\pi}{4}\;;\ \dfrac{3\pi}{4}\;;\ \dfrac{5\pi}{4}\;;\ \dfrac{7\pi}{4}\right\rbrace$ 

5) $\cos x-\cos 3x+\cos 5x=0$
 
La méthode de résolution est analogue à celle du 4). 
 
On a :$$\cos x+\cos 5x=2\cos 3x\cos 2x$$
 
Donc le premier membre se factorise en $\cos 3x(2\cos 2x-1).$ 
 
Cette dernière expression est nulle si et seulement si $\cos 3x=0$ ou $\cos 2x=\dfrac{1}{2}$
 
$\ast\ \cos 3x=0\Leftrightarrow 3x=2k\pi\ (k\in\mathbb{Z})\Leftrightarrow x=\dfrac{2k\pi}{3}\ (k\in\mathbb{Z}).$
 
On obtient, dans $[0\;;\ 2\pi[$ les solutions : $0$, $\dfrac{2\pi}{3}$ et $\dfrac{4\pi}{3}$ (correspondant à $k=0$, $k=1$ et $k=2$ respectivement).
 
$\ast\ \cos 2x=\dfrac{1}{2}\Leftrightarrow\left\lbrace\begin{array}{lcl} x&=&\dfrac{\pi}{3}+2k_{1}\pi\\ \\ x&=&-\dfrac{\pi}{3}+2k'_{1}\pi\quad\text{ou }(k_{1}\;,\ k'_{1}\in\mathbb{Z}) \end{array}\right.$
 
$\Leftrightarrow\left\lbrace\begin{array}{lcl} x&=&\dfrac{\pi}{6}+2k_{1}\pi\\ \\ x&=&-\dfrac{\pi}{6}+2k'_{1}\pi\quad\text{ou }(k_{1}\;,\ k'_{1}\in\mathbb{Z}) \end{array}\right.$
 
On obtient, dans $[0\;;\ 2\pi[$ les solutions :
 
$\dfrac{\pi}{6}$, $\dfrac{7\pi}{6}$ (correspondant à $k_{1}=0$ et $k_{1}=1$ respectivement) et $\dfrac{5\pi}{6}$, $\dfrac{11\pi}{6}$ (correspondant à $k'_{1}=1$ et $k'_{1}=2$ respectivement).
 
6) $4\sin^{2}x+2(1+\sqrt{3})\sin x+\sqrt{3}=0$
 
Le changement de variable $X=\sin x$ ramène l'équation de départ à l'équation du second degré $4X^{2}+2(1+\sqrt{3})X+\sqrt{3}=0$, dont la résolution, laissée au lecteur (penser à écrire le discriminant comme un carré parfait), montre qu'elle a pour solutions : $X_{1}=-\dfrac{1}{2}$ et $X_{2}=-\dfrac{\sqrt{3}}{2}$
 
$\ast\ \sin x=-\dfrac{1}{2}=\sin\left(-\dfrac{\pi}{6}\right)\Leftrightarrow\left\lbrace\begin{array}{lcl} x&=&-\dfrac{\pi}{6}+2k\pi\\ \\ x&=&\dfrac{7\pi}{6}+2k'\pi\quad\text{ou }(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$
 
$\ast\ \sin x=-\dfrac{\sqrt{3}}{2}=\sin\left(-\dfrac{\pi}{3}\right)\Leftrightarrow\left\lbrace\begin{array}{lcl} x&=&-\dfrac{\pi}{3}+2k_{1}\pi\\ \\ x&=&\dfrac{4\pi}{3}+2k'_{1}\pi\quad\text{ou }(k_{1}\;,\ k'_{1}\in\mathbb{Z}) \end{array}\right.$
 
On trouve pour ensemble de solutions dans $[0\;;\ 2\pi[$ :
$$S=\left\lbrace\dfrac{11\pi}{6}\;;\ \dfrac{7\pi}{6}\;;\ \dfrac{5\pi}{3}\;;\ \dfrac{4\pi}{3}\right\rbrace$$
 
7) $\sin x+\sin 2x+\sin 3x=0$
 
D'après la formule de factorisation $\sin p+\sin q=2\sin\dfrac{p+q}{2}\cos\dfrac{p-q}{2}$, on peut écrire :
$$\sin x+\sin 3x=2\sin 2x\cos x$$
 
L'équation devient alors : $\sin 2x(2\cos x+1)=0\Leftrightarrow\sin 2x=0$ ou $\cos x=-\dfrac{1}{2}.$
 
$\ast\ \sin 2x=0\Leftrightarrow 2x=k\pi\Leftrightarrow x=\dfrac{k\pi}{2}.$ 
 
Cette équation a pour ensemble de solutions dans $[0\;;\ 2\pi[$ :
$$S_{1}=\left\lbrace 0\;;\ \dfrac{\pi}{2}\;;\ \pi\;;\ \dfrac{3\pi}{2}\right\rbrace.$$
 
$\ast\ \cos x=-\dfrac{1}{2}\Leftrightarrow\left\lbrace\begin{array}{lcl} x&=&\dfrac{2\pi}{3}+2k\pi\\ \\ x&=&-\dfrac{2\pi}{3}+2k'\pi\quad\text{ou }(k\;,\ k'\in\mathbb{Z})\end{array}\right..$
 
Ce système a pour ensemble de solutions dans $[0\;;\ 2\pi[$ :
$$S_{2}=\left\lbrace\dfrac{2\pi}{3}\;;\ \dfrac{4\pi}{3}\right\rbrace$$
 
L'ensemble des solutions de l'équation est donc :
$$S=S_{1}\cup S_{2}=\left\lbrace 0\;;\ \dfrac{\pi}{2}\;;\ \pi\;;\ \dfrac{3\pi}{2}\;;\ \dfrac{2\pi}{3}\;;\ \dfrac{4\pi}{3}\right\rbrace.$$
 
8) $\sin 2x+\sin 4x=0$
 
D'après la formule donnant le sinus de l'angle double, on a : $\sin 4x=2\sin 2x\cos 2x.$
 
L'équation s'écrit alors : $\sin 2x+2\sin 2x\cos 2x=0$, soit en factorisant par $\sin 2x$ :
$$\sin 2x(1+2\cos 2x)=0.$$
 
Elle est donc équivalente à : $\sin 2x=0$ ou $\cos 2x=-\dfrac{1}{2}$
 
$\ast\ \sin 2x=0\Leftrightarrow 2x=k\pi\Leftrightarrow x=\dfrac{k\pi}{2}.$
 
Cette équation a pour ensemble de solutions dans $[0\;;\ 2\pi[$ :
$$S=S_{1}=\left\lbrace 0\;;\ \dfrac{\pi}{2}\;;\ \pi\;;\ \dfrac{3\pi}{2}\right\rbrace.$$
 
$\ast\ \cos 2x=-\dfrac{1}{2}\Leftrightarrow\left\lbrace\begin{array}{lcl} 2x&=&\dfrac{2\pi}{3}+2k\pi\\ \\ 2x&=&-\dfrac{2\pi}{3}+2k'\pi\quad\text{ou }(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$
 
$\Leftrightarrow\left\lbrace\begin{array}{lcl} x&=&\dfrac{\pi}{3}+k\pi\\ \\ x&=&-\dfrac{\pi}{3}+k'\pi\quad\text{ou }(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$
 
Ce dernier système a pour ensemble de solutions dans $[0\;;\ 2\pi[$ : 
$$S=S_{2}=\left\lbrace\dfrac{\pi}{3}\;;\ \dfrac{4\pi}{3}\;;\ \dfrac{2\pi}{3}\;;\ \dfrac{5\pi}{3}\right\rbrace.$$
 
L'ensemble des solutions de l'équation est donc :
$$S=S_{1}\cup S_{2}=\left\lbrace 0\;;\ \dfrac{\pi}{2}\;;\ \pi\;;\ \dfrac{3\pi}{2}\;;\ \dfrac{\pi}{3}\;;\ \dfrac{4\pi}{3}\;;\ \dfrac{2\pi}{3}\;;\ \dfrac{5\pi}{3}\right\rbrace.$$
 
9) $\cos^{2}x+\dfrac{2}{\sqrt{3}}\sin x\cos x-\sin^{2}x=0$
 
Les formules $\cos 2x=\cos^{2}x-\sin^{2}x$ et $\sin 2x=2\sin x\cos x$ montrent que l'équation est équivalente à : $$\cos 2x+\dfrac{1}{\sqrt{3}}\sin 2x=0\quad(\ast)$$
 
Cette dernière équation est de la forme
$$a\cos u+b\sin u=0.$$
 
Pour la résoudre, on divise par $\sqrt{a^{2}+b^{2}}$ et on utilise une formule d'addition. 
 
Ici $\sqrt{a^{2}+b^{2}}=\sqrt{1+\dfrac{1}{3}}=\dfrac{2}{\sqrt{3}}.$
 
On doit donc multiplier les deux membres de l'équation $(\ast)$ par $\dfrac{\sqrt{3}}{2}$, d'où :
 
$(\ast)\Leftrightarrow\dfrac{\sqrt{3}}{2}\cos 2x+\dfrac{1}{2}\sin 2x=0\Leftrightarrow\cos\left(\dfrac{\pi}{6}-2x\right)=0\Leftrightarrow\dfrac{\pi}{6}-2x=2k\pi\ (k\in\mathbb{Z})$
$$\Leftrightarrow x=\dfrac{\pi}{12}+k\pi.$$
 
L'ensemble des solutions dans $[0\;;\ 2\pi[$ est : 
$$S=\left\lbrace\dfrac{\pi}{12}\;;\ \dfrac{13\pi}{12}\right\rbrace$$ 
 
10) $\sin^{6}x+\cos^{6}x=\dfrac{1}{4}$
 
En posant $a=\sin^{2}x$ et $b=\cos^{2}x$, l'équation s'écrit : $a^{3}+b^{3}=\dfrac{1}{4}$, soit d'après les formules d'identités remarquables étudiées en Seconde : $(a+b)(a^{2}-ab+b^{2})=\dfrac{1}{4}.$
 
Par ailleurs, on a :
$$a^{2}+b^{2}=(a+b)^{2}-2ab$$
 
Tenant compte du fait que $a+b=1$, (identité trigonométrique fondamentale), notre équation devient :
 
$1-3ab=\dfrac{1}{4}$, soit :
 
$\sin^{2}x\cos^{2}x=\dfrac{1}{4}\Leftrightarrow\left(\dfrac{1}{2}\sin 2x\right)^{2}=\dfrac{1}{4}\Leftrightarrow(\sin 2x)^{2}=1\Leftrightarrow(\sin 2x=1\text{ ou }\sin 2x=-1).$
 
Cette dernière condition équivaut au fait que $2x$ est un multiple impair de $\dfrac{\pi}{2}$, en d'autres termes qu'on a : $$2x=(2k+1)\dfrac{\pi}{2}\Leftrightarrow x=(2k+1)\dfrac{\pi}{4}\ (k\in\mathbb{z}).$$
 
Dans $[0\;;\ 2\pi[$, on obtient comme ensemble de solutions les nombres : $\dfrac{\pi}{4}$, $\dfrac{3\pi}{4}$, $\dfrac{5\pi}{4}$, $\dfrac{7\pi}{4}.$
 
11) $\sqrt{3}\tan^{2}x+(1+\sqrt{3})\tan x+1=0$
 
Le changement de variable $X=\tan x$ ramène cette équation en l'équation du second degré :
$$\sqrt{3}X^{2}+(1+\sqrt{3})X+1=0$$
 
On vérifie aisément que cette dernière a pour solutions $-\dfrac{1}{\sqrt{3}}$
et $-1.$ 
 
L'équation est donc équivalente à $\tan x=-\dfrac{1}{\sqrt{3}}=\tan\left(-\dfrac{\pi}{6}\right)$ ou $\tan x=-1=\tan\left(-\dfrac{\pi}{4}\right)$, 
 
soit $\left\lbrace\begin{array}{lcl} x&=&-\dfrac{\pi}{6}+k\pi\\ \\ x&=&-\dfrac{\pi}{4}+k'\pi\quad(k\;,\ k'\in\mathbb{Z}) \end{array}\right.$
 
On obtient dans $[0\;;\ 2\pi[$ l'ensemble de solutions suivant : 
$$S=\left\lbrace\dfrac{5\pi}{6}\;;\ \dfrac{11\pi}{6}\;;\ \dfrac{3\pi}{4}\;;\ \dfrac{7\pi}{4}\right\rbrace$$
 

Exercice 4

1) On a $\cos^{2}x+\sin^{2}x=1$, d'où $\sin^{2}x=1-\cos^{2}x=1-\left(-\dfrac{3}{5}\right)^{2}=\dfrac{16}{25}.$ 
 
On en déduit que :
 
$\sin x=\dfrac{4}{5}$ ou $\sin x=-\dfrac{4}{5}.$
 
L'hypothèse $x\in\left]\dfrac{\pi}{2}\;;\ \pi\right[$  entraîne que $\sin x>0.$
 
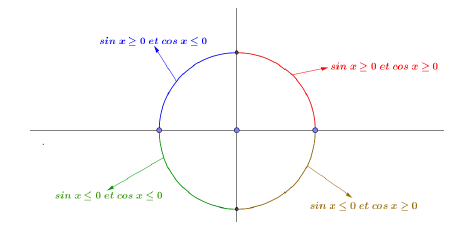
Nous rappelons ci-dessous les signes du sinus et du cosinus sur chaque cadran.
 
 
 
Par suite, on a $\sin x=\dfrac{4}{5}$ et $\tan x=\dfrac{\sin x}{\cos x}=\dfrac{\dfrac{4}{5}}{-\dfrac{3}{5}}$, soit $\tan x=-\dfrac{4}{3}.$
 
2) Méthode analogue à celle du 1). 
 
On trouve $\sin x=-\dfrac{2}{3}$ et $\tan x=-\dfrac{2}{\sqrt{5}}.$ 
 
3) Méthode analogue à celle du 1). 
 
On trouve $\sin x=\dfrac{5}{13}$ et $\tan x=-\dfrac{5}{\sqrt{12}}.$ 

Exercice 5

1) On a d'après la première hypothèse : $\tan x=\dfrac{\sin x}{\cos x}=-2\Rightarrow\sin x=-2\cos x\quad(1)$ et $\cos^{2}x+\sin^{2}x=1\quad(2)$ (identité trigonométrique fondamentale), d'où en substituant l'expression de $\sin x$ donnée par (1) dans (2) : 
 
$\cos^{2}x+(-2\cos x)^{2}=1\Rightarrow\cos^{2}x=\dfrac{1}{5}\quad(3)$ et par une nouvelle application de (2), on en tire que : $\sin^{2}x=\dfrac{4}{5}\quad(4).$
 
La deuxième hypothèse $\left(x\in]0\;;\ \pi[\right)$ entraîne que $\sin x>0$, ce qui, joint avec (4), fournit $\sin x=\dfrac{2}{\sqrt{5}}\quad(5).$
 
Des relations (1) et (5), on tire alors facilement : $\cos x=-\dfrac{1}{\sqrt{5}}.$ 
 
2) Méthode analogue à celle du 1). 
 
On trouve : $\sin x=-\dfrac{11}{61}\text{ et }\cos x=-\dfrac{60}{61}.$
 
3) Méthode analogue à celle du 1). 
 
On trouve : $\sin x=-\dfrac{8}{17}$ et $\cos x=\dfrac{15}{17}.$ 

Exercice 6

1) Le fait que $x\in\left]\dfrac{\pi}{2}\;;\ \pi\right[$  assure que $\cos x<0.$
 
En appliquant l'identité trigonométrique fondamentale, on a : $\dfrac{2}{3}+\cos^{2}x=1\Rightarrow\cos^{2}x=\dfrac{1}{3}.$
 
Il résulte de tout cela qu'on a $\cos x=-\dfrac{1}{\sqrt{3}}.$
 
Par suite $\tan x=\dfrac{\sin x}{\cos x}=\dfrac{\sqrt{\dfrac{2}{3}}}{\dfrac{1}{\sqrt{3}}}$, soit $\tan x=-\sqrt{2}.$
 
2) Méthode analogue à celle du 1). 
 
On trouve : $\cos x=-\dfrac{3}{5}$ et $\tan x=\dfrac{4}{3}.$
 
3) Méthode analogue à celle du 1). 
 
On trouve : $\cos x=\dfrac{\sqrt{7}}{3}$ et $\tan x=-\dfrac{\sqrt{14}}{3}.$

Exercice 7

D'après la formule $\tan 2a=\dfrac{2\tan a}{1-\tan^{2}a}$, on a :
 
$\tan 2x=\dfrac{2\left(\sqrt{3}-2\right)}{1-\left(\sqrt{3}-2\right)^{2}}=\dfrac{-4+2\sqrt{3}}{-6+4\sqrt{3}}=\dfrac{(-4+2\sqrt{3})(-6-4\sqrt{3})}{36-48}=\dfrac{4\sqrt{3}}{-12}=-\dfrac{\sqrt{3}}{3}=\tan\left(-\dfrac{\pi}{6}\right)$, d'où :
$$2x=-\dfrac{\pi}{6}+k\pi\ (k\in\mathbb{Z}.$$
 
Et puisque $2x\in]-\pi\;;\ 0[$, on a nécessairement $2x=-\dfrac{\pi}{6}$  et par suite $x=-\dfrac{\pi}{12}.$

Exercice 8

On a $\cos 2x=1-2\left(\dfrac{\sqrt{2}+\sqrt{6}}{4}\right)^{2}=1-\dfrac{8+4\sqrt{3}}{8}=-\dfrac{\sqrt{3}}{2}$ (d'après la formule $\cos 2x=1-2\sin^{2}x$) d'où, puisque $2x\in]-\pi\;;\ 0[$, et par suite $x=\dfrac{5\pi}{12}.$

Inéquations trigonométrique

Exercice 9

Les solutions sont données dans $]-\pi\;;\ \pi]$ et dans $[0\;;\ 2\pi[$, accompagnées chaque fois d'un graphique où l'ensemble des solutions est colorié.
 
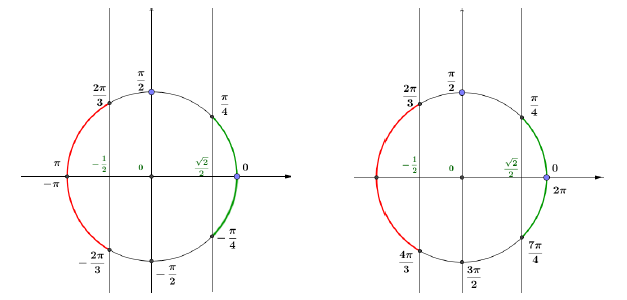
1) $2\cos x+1>0$
 
L'inéquation équivaut à $\cos x>-\dfrac{1}{2}.$
 
 
 
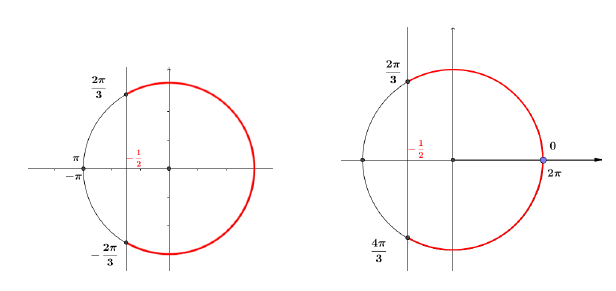
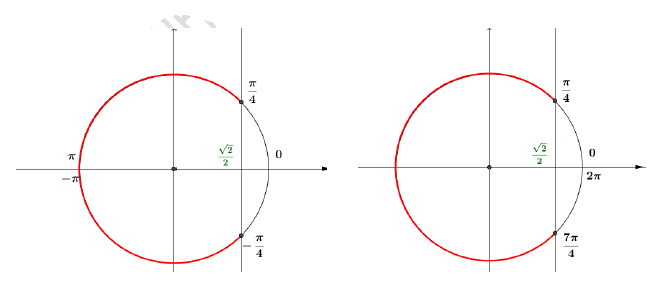
$S_{]-\pi\;;\ \pi]}=\left]-\dfrac{-2\pi}{3}\;;\ \dfrac{2\pi}{3}\right[$ et $S_{[0\;;\ 2\pi]}=\left[0\;;\ \dfrac{2\pi}{3}\right[\cup\left]\dfrac{4\pi}{3}\;;\ 2\pi\right]$
 
2) L'inéquation équivaut à $\cos x\leq\dfrac{1}{\sqrt{2}}$, soit à $\cos x\leq\cos\dfrac{\pi}{4}.$
 
 
 
$S_{]-\pi\;;\ \pi]}=\left[-\pi\;;\ -\dfrac{\pi}{4}\right]\cup\left[\dfrac{\pi}{4}\;;\ \pi\right]$ et 
 
$S_{[0\;;\ 2\pi[}=\left[\dfrac{\pi}{4}\;;\ \dfrac{7\pi}{4}\right]$
 
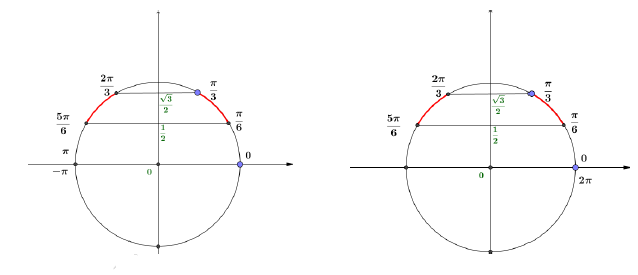
3) $1-2\sin x\leq 0$
 
L'inéquation équivaut à $\sin x\geq\dfrac{1}{2}$, soit à $\sin x\geq\sin\left(\dfrac{\pi}{6}\right).$
 
 
 
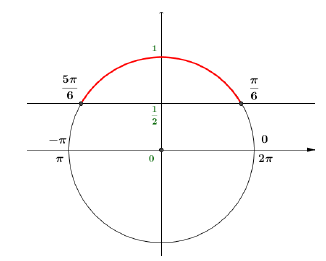
$S_{[0\;;\ 2\pi[}=S_{]-\pi\;;\ \pi]}=\left[\dfrac{\pi}{6}\;;\ \dfrac{5\pi}{6}\right]$
 
4) $2\sin x-\sqrt{3}<0$
 
L'inéquation équivaut à $\sin x<\dfrac{\sqrt{3}}{2}$, soit à $\sin x<\sin\left(\dfrac{\pi}{3}\right).$
 
 
 
$S_{]-\pi\;;\ \pi]}=\left[-\pi\;;\ \dfrac{\pi}{3}\right[\cup\left]\dfrac{2\pi}{3}\;;\ \pi\right]$ et 
 
$S_{[0\;;\ 2\pi[}=\left[0\;;\ \dfrac{\pi}{3}\right[\cup\left]\dfrac{2\pi}{3}\;;\ 2\pi\right].$
 
5) $\tan x>1$
 
L'inéquation équivaut à $\tan x>\tan\left(\dfrac{\pi}{4}\right)$
 
 
 
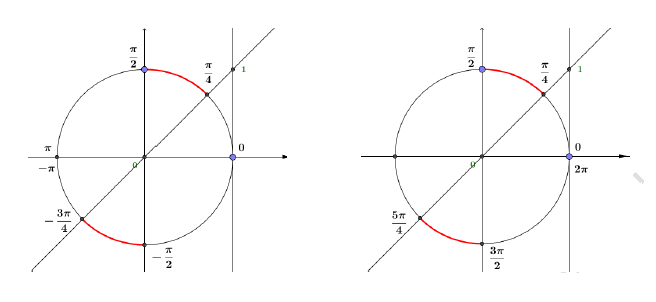
$S_{]-\pi\;;\ \pi]}=\left]-\dfrac{3\pi}{4}\;;\ -\dfrac{\pi}{2}\right[\cup\left]\dfrac{\pi}{4}\;;\ \dfrac{\pi}{2}\right[$ et 
 
$S_{[0\;;\ 2\pi[}=\left]\dfrac{\pi}{4}\;;\ \dfrac{\pi}{2}\right[\cup\left]\dfrac{5\pi}{4}\;;\ \dfrac{3\pi}{2}\right].$
 
6) $\sqrt{3}\tan x-3\leq 0$
 
 
 
L'inéquation équivaut à $\tan x\leq\sqrt{3}$, soit à $\tan x\leq\tan\left(\dfrac{\pi}{3}\right).$
 
 
 
$S_{]-\pi\;;\ \pi]}=\left[-\pi\;;\ -\dfrac{2\pi}{3}\right]\cup\left]-\dfrac{\pi}{2}\;;\ \dfrac{\pi}{3}\right]\cup\left]\dfrac{\pi}{2}\;;\ \pi\right]$ et 
 
$S_{[0\;;\ 2\pi[}=\left[0\;;\ \dfrac{\pi}{3}\right]\cup\left]\dfrac{\pi}{2}\;;\ \dfrac{4\pi}{3}\right]\cup\left]\dfrac{3\pi}{2}\;;\ 2\pi\right[.$
 
7) $4\cos^{2}x-2(\sqrt{2}-1)\cos x-\sqrt{2}>0$
 
Le changement de variable $X=\cos x$ transforme l'inéquation proposée en l'inéquation du second degré : 
 
$4X^{2}-2(\sqrt{2}-1)-\sqrt{2}>0\quad(\ast).$ 
 
Le premier membre de cette dernière est un trinôme qui a pour discriminant réduit $$\Delta'=\left(\sqrt{2}-1\right)^{2}+4\sqrt{2}=3+2\sqrt{2}=\left(\sqrt{2}+1\right)^{2}.$$
 
Par conséquent, il a pour racines $X_{1}=\dfrac{\sqrt{2}-1-(\sqrt{2}+1)}{4}=-\dfrac{1}{2}$ et $X_{2}=\dfrac{\sqrt{2}-1+(\sqrt{2}+1)}{4}=\dfrac{\sqrt{2}}{2}.$
 
L'ensemble des solutions de $(\ast)$ est, d'après les règles sur le signe d'un trinôme :
$$\left]-\infty\;;\ -\dfrac{1}{2}\right[\cup\left]\dfrac{\sqrt{2}}{2}\;;\ +\infty\right[.$$
 
L'inéquation de départ est donc équivalente à $\cos x-\dfrac{1}{2}$ ou $\cos x>\dfrac{\sqrt{2}}{2}.$
 
Nous représentons les solutions de ces deux inéquations dans la figure ci-dessous.
 
 
 
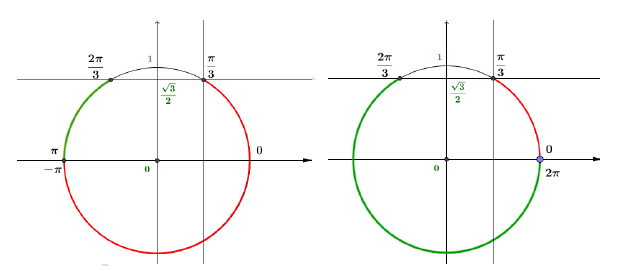
$S_{]-\pi\;;\ \pi]}=\left[-\pi\;;\ -\dfrac{2\pi}{3}\right[\cup\left]-\dfrac{\pi}{4}\;;\ \dfrac{\pi}{4}\right[\cup\left]\dfrac{2\pi}{3}\;;\ \pi\right]$ et 
 
$S_{[0\;;\ 2\pi[}=\left[0\;;\ \dfrac{\pi}{4}\right[\cup\left]\dfrac{2\pi}{3}\;;\ \dfrac{4\pi}{3}\right[\cup\left]\dfrac{7\pi}{4}\;;\ 2\pi\right].$
 
8) $4\sin^{2}x-2\left(1+\sqrt{3}\right)\sin x+\sqrt{3}\leq 0$
 
Méthode analogue à celle de l'inéquation précédente. 
 
Le changement de variable $X=\sin x$ transforme l'inéquation proposée en l'inéquation du second degré :
$$4X^{2}-2\left(1+\sqrt{3}\right)X+\sqrt{3}\leq 0\quad(\ast).$$
 
Le premier membre de cette dernière est un trinôme qui a pour discriminant réduit $\Delta'=\left(1+\sqrt{3}\right)^{2}-4\sqrt{3}=4-2\sqrt{3}=\left(\sqrt{3}-1\right)^{2}.$
 
Par conséquent, il a pour racines $X_{1}=\dfrac{1+\sqrt{3}-\left(\sqrt{3}-1\right)}{4}$ et $X_{2}=\dfrac{1+\sqrt{3}\left(\sqrt{3}-1\right)}{4}.$
 
L'ensemble des solutions de $(\ast)$ est, d'après les règles sur le signe d'un trinôme : $\left[\dfrac{1}{2}\;;\ \dfrac{\sqrt{3}}{2}\right].$
 
L'inéquation de départ est donc équivalente à $\dfrac{1}{2}\leq\sin x\leq\dfrac{\sqrt{3}}{2}.$
 
Nous représentons les solutions de cette double inéquation dans la figure ci-dessous.
 
 
 
$S_{[0\;;\ 2\pi[}=S_{]-\pi\;;\ \pi[}=\left[\dfrac{\pi}{6}\;;\ \dfrac{\pi}{3}\right]\cup\left[\dfrac{2\pi}{3}\;;\ \dfrac{5\pi}{6}\right].$
 
9) $-4\cos^{2}x+2\left(\sqrt{2}+1\right)\sin x+4+\sqrt{2}\leq 0$
 
On remplace dans l'inéquation $\cos^{2}x$ par $1-\sin^{2}x$ pour obtenir :
$$4\sin^{2}x+2\left(1+\sqrt{2}\right)\sin x+\sqrt{2}\leq 0.$$
 
Le changement de variable $X=\sin x$ transforme cette dernière inéquation en l'inéquation du second degré :
$$4X^{2}+2\left(1+\sqrt{2}\right)X+\sqrt{2}\leq 0\quad(\ast).$$
 
Le premier membre de cette dernière est un trinôme qui a pour discriminant réduit $$\Delta'=\left(1+\sqrt{2}\right)^{2}-4\sqrt{2}=3-2\sqrt{2}=\left(\sqrt{2}-1\right)^{2}.$$
 
Par conséquent, il a pour racines $X_{1}=\dfrac{-(1+\sqrt{2})-(\sqrt{2}-1)}{4}=-\dfrac{\sqrt{2}}{2}$ et $X_{2}=\dfrac{-(1+\sqrt{2})+(\sqrt{2}-1)}{4}=-\dfrac{1}{2}.$
 
L'ensemble des solutions de $(\ast)$ est, d'après les règles sur le signe d'un trinôme : $\left[-\dfrac{\sqrt{2}}{2}\;;\ -\dfrac{1}{2}\right].$
 
L'inéquation de départ est donc équivalente à $-\dfrac{\sqrt{2}}{2}\leq\sin x\leq-\dfrac{1}{2}$
 
 
 
$S_{]-\pi\;;\ \pi]}=\left[-\dfrac{5\pi}{6}\;;\ -\dfrac{3\pi}{4}\right]\cup\left[-\dfrac{\pi}{4}\;;\ -\dfrac{\pi}{6}\right].$
 
et $S_{[0\;;\ \pi]}=\left[\dfrac{7\pi}{6}\;;\ \dfrac{5\pi}{4}\right]\cup\left[\dfrac{7\pi}{4}\;;\ \dfrac{11\pi}{6}\right].$
 
10) $4\sin^{2}x+2\left(1-\sqrt{3}\right)\cos x-4+\sqrt{3}\leq 0$
 
On remplace dans l'inéquation $\sin^{2}x$ par $1-\cos^{2}x$ pour obtenir :
$$-4\cos^{2}x+2\left(1-\sqrt{3}\right)\cos x+\sqrt{3}\leq 0.$$
 
Le changement de variable $X=\cos x$ transforme cette dernière inéquation en l'inéquation du second degré :
$$-4X^{2}+2\left(1-\sqrt{3}\right)X+\sqrt{3}\leq 0\quad(\ast).$$
 
Le premier membre de cette dernière est un trinôme qui a pour discriminant réduit

Exercice 10

Nous donnons les résultats sous la forme d'un tableau. 
 
Il suffit d'appliquer les formules des angles associés et « d'éliminer » les multiples de $2\pi$ dans les cosinus et les sinus ou les multiples de $\pi$ dans les tangentes et les cotangentes.
$$\begin{array}{|c|c|c|c|c|} \hline &\cos&\sin&\tan&co\tan\\ \hline -\alpha-5\pi&-\cos\alpha&-\sin\alpha&\tan\alpha&co\tan\alpha\\ \hline -\alpha-\pi&-\cos\alpha&\sin\alpha&-\tan\alpha&-co\tan\alpha\\ \hline -\alpha-2\pi&-\cos\alpha&-\sin\alpha&-\tan\alpha&-co\tan\alpha\\ \hline -\alpha-\dfrac{\pi}{2}&-\sin\alpha&-\cos\alpha&co\tan\alpha&\tan\alpha\\ \hline \alpha-\dfrac{9\pi}{2}&\sin\alpha&-\cos\alpha&-co\tan\alpha&-\tan\alpha\\ \hline -\alpha+\dfrac{5\pi}{2}&\sin\alpha&\cos\alpha&co\tan\alpha&\tan\alpha\\ \hline \end{array}$$

Exercice 11

Nous donnons les résultats sous forme de tableaux. 
 
Appliquer les formules relatives aux valeurs remarquables des lignes trigonométriques, les formules des angles associés et « éliminer » les multiples de $2\pi$ dans les cosinus et les sinus ou les multiples de $\pi$ dans les tangentes et les cotangentes.
$$a)\qquad\begin{array}{|c|c|c|c|c|} \hline &\cos&\sin&\tan&co\tan\\ \hline 3\pi&-1&0&0&\text{Non définie}\\ \hline -5\pi&-1&0&0&\text{Non définie}\\ \hline \dfrac{3\pi}{2}&0&-1&\text{Non définie}&0\\ \hline \end{array}$$
 
$$b)\qquad\begin{array}{|c|c|c|c|c|} \hline &\cos&\sin&\tan&co\tan\\ \hline \dfrac{3\pi}{4}&-\dfrac{\sqrt{2}}{2}&\dfrac{\sqrt{2}}{2}&-1&-1\\ \hline -\dfrac{7\pi}{4}&\dfrac{\sqrt{2}}{2}&\dfrac{\sqrt{2}}{2}&1&1\\ \hline \dfrac{15\pi}{4}&\dfrac{\sqrt{2}}{2}&-\dfrac{\sqrt{2}}{2}&-1&-1\\ \hline \end{array}$$
 
$$c)\qquad\begin{array}{|c|c|c|c|c|} \hline &\cos&\sin&\tan&co\tan\\ \hline -\dfrac{2\pi}{3}&-\dfrac{1}{2}&-\dfrac{\sqrt{3}}{2}&\sqrt{3}&\dfrac{1}{\sqrt{3}}\\ \hline \dfrac{5\pi}{3}&\dfrac{1}{2}&-\dfrac{\sqrt{3}}{2}&-\sqrt{3}&-\dfrac{1}{\sqrt{3}}\\ \hline \dfrac{8\pi}{3}&-\dfrac{1}{2}&-\dfrac{\sqrt{3}}{2}&\sqrt{3}&-\dfrac{1}{\sqrt{3}}\\ \hline \end{array}$$
 
$$d)\qquad\begin{array}{|c|c|c|c|c|} \hline &\cos&\sin&\tan&co\tan\\ \hline \dfrac{7\pi}{6}&-\dfrac{\sqrt{3}}{2}&-\dfrac{1}{2}&\dfrac{1}{\sqrt{3}}&\sqrt{3}\\ \hline \dfrac{13\pi}{6}&\dfrac{\sqrt{3}}{2}&\dfrac{1}{2}&\dfrac{1}{\sqrt{3}}&\sqrt{3}\\ \hline \dfrac{31\pi}{6}&-\dfrac{\sqrt{3}}{2}&-\dfrac{1}{2}&\dfrac{1}{\sqrt{3}}&\sqrt{3}\\ \hline \end{array}$$

Exercice 12

En appliquant les formules des angles associés, on obtient :
 
$\begin{array}{lcl}A&=&\cos\alpha-\cos\alpha-\cos\alpha+\cos\alpha\\&=&0\end{array}$
 
$\begin{array}{lcl}B&=&co\tan\alpha-co\tan\alpha+3co\tan\alpha+co\tan\alpha\\&=&2co\tan\alpha\end{array}$
 
Si $k$ est pair, on a :
 
$\begin{array}{lcl}C&=&\dfrac{-\sin 3\alpha+\sin 3\alpha+\sin 3\alpha}{-\cos 3\alpha+\cos 3\alpha-3\cos 3\alpha}\\&=&\dfrac{\sin 3\alpha}{-3\cos 3\alpha}\\&=&-\dfrac{1}{3}\tan 3\alpha\end{array}$
 
Si $k$ est impair, on a : 
 
$\begin{array}{lcl}D&=&\dfrac{-\sin 3\alpha+\sin 3\alpha-\sin 3\alpha}{-\cos 3\alpha-\cos 3\alpha-3\cos 3\alpha}\\&=&\dfrac{-\sin 3\alpha}{-5\cos 3\alpha}\\&=&\dfrac{1}{5}\tan 3\alpha.\end{array}$

Exercice 13

1) $f(x)=\sin 2x+\sin^{2}x-2\sin x\cos x+\cos^{2}x.$ 
 
Or $\sin 2x=2\sin x\cos x$ et $\sin^{2}x+\cos^{2}x=1$, d'où $f(x)=1$ pour tout réel $x.$
 
2) On a $\begin{array}{lcl}\cos\left(\dfrac{2\pi}{3}+x\right)&=&\cos\dfrac{2\pi}{3}\cos x-\sin\dfrac{2\pi}{3}\sin x\\&=&-\dfrac{1}{2}\cos x-\dfrac{\sqrt{3}}{2}\sin x.\end{array}$
 
D'où : $\cos^{2}\left(\dfrac{2\pi}{3}+x\right)=\dfrac{1}{4}\cos^{2}x+\dfrac{3}{4}\sin^{2}x+\dfrac{\sqrt{3}}{4}sin x\cos x.$
 
De même : $\begin{array}{lcl}\cos\left(\dfrac{2\pi}{3}-x\right)&=&\cos\dfrac{2\pi}{3}\cos x+\sin \dfrac{2\pi}{3}\sin x\\&=&-\dfrac{1}{2}\cos x+\dfrac{\sqrt{3}}{2}\sin x.\end{array}$
 
D'où : $\cos^{2}\left(\dfrac{2\pi}{3}-x\right)=\dfrac{1}{4}\cos^{2}x+\dfrac{3}{4}\sin^{2}x-\dfrac{\sqrt{3}}{4}\sin x\cos x.$
 
En additionnant, il vient :
 
$\begin{array}{lcl}\cos^{2}x+\cos^{2}\left(\dfrac{2\pi}{3}+x\right)+\cos^{2}\left(\dfrac{2\pi}{3}-x\right)&=&\cos^{2}x+\dfrac{1}{2}\cos^{2}x+\dfrac{3}{2}\sin^{2}x\\&=&\dfrac{3}{2}(\cos^{2}x+\sin^{2}x)\end{array}$

soit $f(x)=\dfrac{3}{2}$ pour tout réel $x$, d'après l'identité trigonométrique fondamentale.

 
3) Démarche analogue au 2) ci-dessus. 
 
On développe les carrés en utilisant les formules d'addition relatives au sinus.

On trouve aussi que $f(x)=\dfrac{3}{2}$ pour tout réel $x.$

Exercice 14

1) Développer $\sqrt{2}\sin\left(\dfrac{\pi}{4}+x\right)$ par la formule d'addition.
 
2) Même méthode.
 
3) On a d'après les formules de factorisation :
 
$\cos x+\cos 4x=2\cos\dfrac{5x}{2}\cos x$ et $\cos 2x+\cos 3x=2\cos\dfrac{5x}{2}\cos x.$
 
D'où le résultat en faisant la somme et en factorisant par $2\cos\dfrac{5x}{2}.$
 
4) On a d'après les formules de factorisation :
 
$\sin x+\sin 4x=2\sin\dfrac{5x}{2}\cos\dfrac{3x}{2}$ et $\sin 2x+\sin 3x=2\sin\dfrac{5x}{2}\cos\dfrac{x}{2}$
 
En faisant la somme, on a :
 
$\sin x+\sin 2x+\sin 3x+\sin 4x=2\sin\dfrac{5x}{2}\left(\cos\dfrac{3x}{2}+\cos\dfrac{x}{2}\right)$, puis en appliquant une nouvelle fois une formule de factorisation à la parenthèse, on obtient :
 
$\sin x+\sin 2x+\sin 3x+\sin 4x=4\sin\dfrac{5x}{2}\cos x\cos\dfrac{x}{2}.$
 
5) D'après la formule de transformation $\sin a\sin b=\dfrac{1}{2}[\cos(a-b)-\cos(a+b)]$, on a :
 
$\begin{array}{lcl}\sin\left(\dfrac{\pi}{3}-x\right)\sin\left(\dfrac{\pi}{3}+x\right)&=&\dfrac{1}{2}\left[\cos(-2x)-\cos\left(\dfrac{2\pi}{3}\right)\right]\\&=&\dfrac{1}{2}\left[\cos(-2x)+\dfrac{1}{2}\right].\end{array}$
 
D'où en multipliant les deux membres par $4\sin x$ :
 
$\begin{array}{lcl}4\sin x\sin\left(\dfrac{\pi}{3}-x\right)\sin\left(\dfrac{\pi}{3}+x\right)&=&2\sin x\cos 2x+\sin x\\&=&2\sin x\left(\dfrac{1}{2}+\cos 2x\right)\\&=&\sin x(1+2\cos 2x)\end{array}$ 
 
D'autre part, d'après la formule d'addition relative au sinus et les formules de duplication, on a : 
 
$\begin{array}{lcl}\sin 3x&=&\sin(2x+x)\\&=&\sin 2x\cos x+\cos 2x\sin x\\&=&2\sin x\cos^{2}x+\cos 2x\sin x\\&=&\sin x(\cos 2x+2\cos^{2}x)\\&=&\sin x(\cos 2x+1+\cos 2x)\\&=&\sin x(1+2\cos 2x).\end{array}$
 
L'égalité proposée en résulte.
 
Auteur: 
Mouhamadou ka

Commentaires

Mamadou Malal Balde (non vérifié)

lun, 09/21/2020 - 21:32

Trésor bien

El Hadji ka (non vérifié)

mar, 05/25/2021 - 02:23

Bonjour Mr ka tous nos remerciements

Ajouter un commentaire