Vous êtes ici

Solution série d'exercices : Puissances dans D - 5e

Classe:

Cinquième

Exercice 1

1)Écrivons les nombres ci-dessous en lettres

$3^{4}$ : trois à la puissance $4$

$6^{5}$ : Six à la puissance $5$

$15^{4}$ : Quinze à la puissance $4$

$7^{15}$ : Sept à la puissance $15$

2) Le nombre $3^{5}$ est le produit de cinq facteurs égaux à $3.$ Faisons de même pour chacun des nombres ci-dessous.

$3^{4}$ est le produit de quatre facteurs égaux à $3$

$6^{5}$ est le produit de cinq facteurs égaux à $6$

$15^{4}$ est le produit de quatre facteurs égaux à $15$

$7^{15}$ est le produit de quinze facteurs égaux à $7$

Exercice 2

1) Écrivons chacune des expressions suivantes sous forme d'un produit de facteurs

a) $M_{1}=7^{3}$ ; $M_{2}=4^{5}$ ; $M_{3}=5^{4}$ ; $M_{4}=2^{1}$

$M_{1}=7^{3}=7\times 7\times 7$

$M_{2}=4^{5}=4\times 4\times 4\times 4\times 4$

$M_{3}=5^{4}=5\times 5\times 5\times 5$

$M_{4}=2^{1}=2$

b) $M_{1}=(1.5)^{4}$ ; $M_{2}=(3.5)^{3}$ ; $M_{3}=a^{7}$

$M_{1}=(1.5)^{4}=1.5\times 1.5\times 1.5\times 1.5$

$M_{2}=(3.5)^{3}=3.5\times 3.5\times 3.5$

$M_{3}=(a)^{7}=a\times a\times a\times a\times a\times a\times a$

2) Écrivons chacune des expressions suivantes sous la forme de puissance simple

$A=3\times 3\times 3\times 3=3^{5}$

$B=n\times n\times n\times n\times n\times n=n^{6}$

$C=2.5\times 2.5\times 2.5\times 2.5=(2.5)^{4}$

$D=2\times 7\times 2\times 7\times 2\times 7\times 2=2^{4}\times 7^{3}$

Exercice 3

1) Calculons chacune des puissances ci-dessous

$4^{3}=4\times 4\times 4=64$

$2^{5}=2\times 2\times 2\times 2\times 2=32$

$1.5^{4}=1.5\times 1.5\times 1.5\times 1.5=5.0625$

$1.2^{4}=1.2\times 1.2\times 1.2\times 1.2=2.0736$

2) Mettons chacun des nombres entiers naturels sous la forme de puissances simples

$8=2\times 2\times 2=2^{3}$

$18=2\times 3\times 3=2\times 3^{2}$

$36=6\times 6=2\times 3 \times 2 \times 3=2^{2}\times 3^{2}$

$16=2\times 2\times 2\times 2 = 2^{4}$

$32=2\times 16 = 2\times 2^{4}=2^{5}$

$125=5\times 5\times 5=5^{3}$

Exercice 4

1) Mettons sous la forme de puissances simples

On rappelle que si $a$ est un nombre décimal, $m\ $ et $n\ $ deux entiers naturels alors, on a :

$$a^{m}\times a^{n}=a^{m+n}$$

En appliquant cette propriété de la puissance dans $\mathbb{D}$, on obtient :

$\begin{array}{rcl} A&=&2^{4}\times 2^{5}\times 2^{2}\\\\&=&2^{4+5+2}\\\\&=&2^{11}\end{array}$

Donc, $\boxed{A=2^{11}}$

$\begin{array}{rcl} B&=&3^{6}\times 3^{3}\times 3^{4}\\\\&=&3^{6+3+4}\\\\&=&3^{13}\end{array}$

Alors, $\boxed{B=3^{13}}$

$\begin{array}{rcl} C&=&2^{5}\times 7^{2}\times 2^{3}\times 7^{4}\\\\&=&2^{5+3}\times7^{2+4}\\\\&=&2^{8}\times 7^{6}\end{array}$

Ainsi, $\boxed{C=2^{8}\times 7^{6}}$

$\begin{array}{rcl} D&=&a^{3}\times n^{3}\times a^{5}\times n^{7}\times a\times n\\\\&=&a^{3+5+1}\times n^{3+7+1}\\\\&=&a^{9}\times n^{11}\end{array}$

Donc, $\boxed{D=a^{9}\times n^{11}}$

2) Écrivons sous la forme de puissances simples

On rappelle que si $a$ est un nombre décimal, $m\ $ et $n\ $ deux entiers naturels alors, on a :

$$(a^{m})^{n}=a^{m\times n}$$

En appliquant cette propriété de la puissance dans $\mathbb{D}$, on obtient :

a) $(2^{3})^{2}=2^{3\times 2}=2^{6}$

b) $(7^{4})^{2}=7^{4\times 2}=7^{8}$

c) $(11^{11})^{11}=11^{11\times 11}=11^{121}$

3) Mettons sous la forme de puissance simple

On rappelle que si $a\ $ et $\ b$ sont deux nombres décimaux et $n$ un entier naturel alors, on a :

$$(a\times b)^{n}=a^{n}\times b^{n}$$

En appliquant cette propriété de la puissance dans $\mathbb{D}$, on obtient :

a) $(2\times 3)^{3}=2^{3}\times 3^{3}$

b) $(1.7\times 5)^{3}=(1.7)^{3}\times 5^{3}$

c) $(3^{3}\times 2^{3})^{5}=(3^{3})^{5}\times (2^{3})^{5}=3^{15}\times 2^{15}$

Exercice 5

Écrivons chacune des expressions suivantes sous la forme de puissances simple.

Pour cela, on applique les propriétés de la puissance dans $\mathbb{D}.$

On obtient alors :

$\begin{array}{rcl} A&=&(2\times{3})^{4}\times 2^{4}\times 3^{5}\\ \\&=&2^{4}\times 3^{4}\times 2^{4}\times 3^{5}\\ \\&=&2^{4+4}\times 3^{4+5}\end{array}$

Donc, $\boxed{A=2^{8}\times 3^{9}}$

$\begin{array}{rcl} B&=&(5\times 2)^{5}\times(2^{3}\times 5^{2})^{4}\\ \\&=&5^ 5\times 2^{5}\times 2^{3\times 4}\times 5^{2\times 4}\\ \\&=&5^{5}\times 2^{5}\times 2^{12}\times 5^{8}\\ \\&=&2^{5+12}\times 5^{5+8}\end{array}$

D'où, $\boxed{B=2^{17}\times 5^{13}}$

$\begin{array}{rcl} C&=&3\times 2\times 3^{2}\times 2^{7}\times 3^{2}\\ \\&=&2^{1+7}\times 3^{1+2+2}\end{array}$

Ainsi, $\boxed{C=2^{8}\times 3^{5}}$

$\begin{array}{rcl} D&=&2^{4}\times(3^{2})^{3}\times 2^{6}\times 3^{2}\times 2^{0}\\ \\&=&2^{4}\times 3^{6}\times 2^{6}\times 3^{2}\times 2^{0}\\ \\&=&2^{4+6+0}\times 3^{6+2}\end{array}$

D'où, $\boxed{D=2^{10}\times 3^{8}}$

N.B : $a^{0}=1\;;\ 2^{0}=1$

Tout nombre à la puissance zéro $(0)$ est égal à $1$

Exercice 6

Trouvons la valeur de l'inconnue $x$ pour que l'égalité soit vraie

a) $3^{3}\times 3^{x}=3^{7}$

$3^{3+x}=3^{7}$

Donc, $3+x=7$

C'est à dire ; $x=7-3=4$

Vérification : $\boxed{3^{3}\times 3^{4}=3^{7}}$

b) $(7^{x})^{2}=7^{10}$

$7^{2x}=7^{10}$

Alors, $2x=10$

D'où, $x=\dfrac{10}{2}=5$

Vérification : $\boxed{(7^{5})^{2}=7^{10}}$

c) $2^{4}\times (2^{3})^{x}=4^{13}$

$2^{4}\times (2^{3})^{x}=(2^{2})^{13}$

$2^{4}\times (2^{3})^{x}=2^{26}$

$2^{4}\times 2^{3x}=2^{26}$

$2^{4+3x}=2^{26}$

Donc, $4+3x=26$

Par suite, $3x=26-4$

Ce qui donne : $3x=22$

D'où, $x=\dfrac{22}{3}$

Vérification : $\boxed{2^{4}\times(2^{3})^{\tfrac{22}{3}}=2^{4}\times 2^{22}=2^{26}}$

d) $4^{2}\times (4^{2})^{x}=4^{10}$

$4^{2+2x}=4^{10}$

Donc, $2+2x=10$

Par suite, $2x=10-2=8$

Ainsi, $x=\dfrac{8}{2}=4$

Vérification : $\boxed{4^{2}\times(4^{2})^{4}=4^{10}}$

Exercice 7

Calculons en respectant les règles de la priorité

On rappelle que :

$-\ $ dans une suite d'opérations les parenthèses sont toujours prioritaires.

$-\ $ dans une suite d'opérations sans parenthèses, les calculs des puissances sont prioritaires devant les multiplications et les divisions qui sont prioritaires devant l'addition et la soustraction.

En appliquant ces règles de la priorité, on obtient :

$\begin{array}{rcl} A&=&12.5-3\times(4-3)^{3}+3\times(14-5\div 2)\\ \\&=&12.5-3+[3\times(14-2.5)]\\ \\&=&[12.5-3]+[3\times 11.5]\\ \\&=&[9.5]+[34.5]\\ \\&=&9.5+34.5\end{array}$

D'où, $\boxed{A=44}$

$\begin{array}{rcl} B&=&11.5+1.5\times[17-3\times(14-3^{2})]\times 2\\\\&=&11.5+1.5\times[17-3\times(14-9)]\times 2\\ \\&=&11.5+1.5\times[17-3\times 5]\times 2\\ \\&=&11.5+1.5\times[17-15]\times 2\\ \\&=&11.5+(1.5\times 2)\times 2\\ \\&=&11.5+(3\times 2)\\ \\&=&11.5+6\end{array}$

Donc, $\boxed{B=17.5}$

$\begin{array}{rcl} C&=&5^{3}\div 25+5\times 2+2^{3}\times 5\\ \\&=&(125\div 25)+(5\times 2)+(8\times 5)\\ \\&=&5+10+40\end{array}$

Ainsi, $\boxed{C=55}$

$\begin{array}{rcl} D&=&2^{6}-2^{2}+(2^{4}\times 5-3\times 4)\times(5^{3}-2^{5})\\ \\&=&(2^{6}-2^{2})+[(2^{4}\times 5)-(3\times 4)]\times(5^{3}-2^{5})\\ \\&=&(2^{6}-2^{2})+(80-12)\times(125-32)\\ \\&=&(2^{6}-2^{2})+(68\times 93)\\ \\&=&(2^{6}-2^{2})+6324\\ \\&=&(64-4)+6324\\ \\&=&60+6\,324\end{array}$

D'où, $\boxed{D=6\,384}$

Exercice 8 : "Problème de la vie courante"

Dans un jardin de $36$ arbres, il y a $36$ vautours dans chaque arbre, chaque vautour a donné $36$ œufs, chaque œuf $36$ poussins, chaque poussin $36$ plumes et chaque plume a $36$ barbes.

1) Calculons le nombre total de barbes

On peut procéder comme suit :

$-\ $ Il y a $36$ arbres, et dans chaque arbre il y a $36$ vautours donc,

$\text{nombre total de vautours}=36\times 36$

$-\ $ Chaque vautour a donné $36$ œufs donc,

$\begin{array}{rcl}\text{nombre total d'œufs}&=&(\text{nombre total de vautours})\times 36\\ \\&=&(36\times 36)\times 36\\ \\&=&36\times 36\times 36\end{array}$

$-\ $ Chaque œuf a donné $36$ poussins donc,

$\begin{array}{rcl}\text{nombre total de poussins}&=&(\text{nombre total d'œufs})\times 36\\ \\&=&(36\times 36\times 36)\times 36\\ \\&=&36\times 36\times 36\times 36\end{array}$

$-\ $ Chaque poussin a $36$ plumes donc,

$\begin{array}{rcl}\text{nombre total de plumes}&=&(\text{nombre total de poussins})\times 36\\ \\&=&(36\times 36\times 36\times 36)\times 36\\ \\&=&36\times 36\times 36\times 36\times 36\end{array}$

$-\ $ Enfin, chaque plume a $36$ barbes. Par suite :

$\begin{array}{rcl}\text{nombre total de barbes}&=&(\text{nombre total de plumes})\times 36\\ \\&=&(36\times 36\times 36\times 36\times 36)\times 36\\ \\&=&36\times 36\times 36\times 36\times 36\times 36\\ \\&=&2\,176\,782\,336\end{array}$

Donc, il y a au total $2\,176\,782\,336$ barbes.

2) Mettons ce résultat sous la forme de puissances simples.

On a : $\text{nombre total de barbes}=36\times 36\times 36\times 36\times 36\times 36$

On constate qu'on a répété six $(6)$ fois le terme $36.$

Ce qui donne alors, $36\times 36\times 36\times 36\times 36\times 36=36^{6}$

Exercice 9

On donne : $a=1\;;\ b=2\ $ et $\ c=3.$

1) Calculons :

$M=a^{2}\times b^{3}\times(a^{2}\times b^{3})^{2}\times a\times b$

En remplaçant $a\ $ et $\ b$ par leur valeur, on obtient :

$\begin{array}{rcl} M&=&a^{2}\times b^{3}\times(a^{2}\times b^{3})^{2}\times a\times b\\\\&=&1^{2}\times 2^{3}\times (1^{2}\times 2^{3})^{2}\times 1\times 2\\\\&=&1\times 8\times(1\times 8)^{2}\times 2\\\\&=&8\times 8^{2}\times 2\\\\&=&8\times 64\times 2\\\\&=&1\,024\end{array}$

Donc, $\boxed{M=1\,024}$

Soit : $N=(a^{2}\times c)^{3}\times(a^{2}\times c^{3})\times a^{8}\times c^{0}$

Alors, en remplaçant $a\ $ et $\ c$ par leur valeur, on obtient :

$\begin{array}{rcl} N&=&(a^{2}\times c)^{3}\times(a^{2}\times c^{3})\times a^{8}\times c^{0}\\\\&=&(1^{2}\times 3)^{3}\times(1^{2}\times 3^{3})\times 1^{2}\times 3^{0}\\\\&=&(1\times 3^{3})\times(1\times 27)\times 1\times 1\\\\&=&27\times 27\\\\&=&729\end{array}$

Ainsi, $\boxed{N=729}$

2) Comparer les résultats de $M\ $ et $\ N.$

D'après le résultat de la question $1)$, on a : $M=1\,024\ $ et $\ N=729$

Comme $1\,024$ est supérieur à $729$ alors, on peut dire que le résultat de $M$ est plus grand que celui de $N.$

Exercice 10

Calculons :

$2^{2}=2\times 2=4$

$5^{3}=5\times 5\times 5=125$

$(1.5)^{2}=1.5\times 1.5=2.25$

$(2.1)^{3}=2.1\times 2.1\times 2.1=9.261$

Exercice 11

Complétons chacune des égalités suivantes à l'aide de la puissance d'un nombre :

1) $3\times 3\times 3\times 3\times 3=3^{5}$

2) $1.5\times 1.5\times 1.5\times 1.5\times 1.5\times 1.5=(1.5)^{6}$

3) $3.4\times 3.4\times 3.4\times 3.4=(3.4)^{4}$

Exercice 12

Écrivons chacun des nombres décimaux suivants sous la forme $a^{n}$ avec $n$ entier naturel supérieur ou égal à $2\ :$

$8=2^{3}$

$25=5^{2}$

$27=3^{3}$

$81=3^{4}$

$1\,000=10^{3}$

$0.008=(0.2)^{3}$

$0.25=(0.5)^{2}$

$0.027=(0.3)^{3}$

Exercice 13

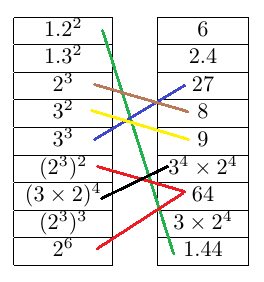
Reproduisons et complétons les tableaux ci-dessous en reliant par une flèche les expressions ayant la même valeur.

Exercice 14

Recopions chacune des égalités ci-dessous et remplaçons le point d'interrogation par l'entier convenable :

$14^{2}=7^{2}\times 2^{2}$

$6^{4}=2^{4}\times 3^{4}$

$(1.3)^{7}=(1.3)^{5}\times(1.3)^{2}$

$a^{n}\times a^{5}=a^{n+5}$

Exercice 15

Recopions et complétons chacune des égalités ci-dessous :

$2^{2}\times 2^{4}=2^{6}$

$(1.4)^{6}\times(1.4)^{4}=(1.4)^{10}$

$a^{2}\times a^{4}\times a^{3}=a^{9}$

Exercice 16

Recopions et complétons chacune des égalités ci-dessous par une puissance d'un nombre décimal :

On rappelle que si $a$ est un nombre décimal, $m\ $ et $n\ $ deux entiers naturels alors, on a :

$$a^{m}\times a^{n}=a^{m+n}$$

En appliquant cette propriété de la puissance dans $\mathbb{D}$, on obtient :

$(14.3)^{2}\times(14.3)^{5}=(14.3)^{2+5}=(14.3)^{7}$

$(0.4)^{7}\times(0.4)^{5}=(0.4)^{7+5}=(0.4)^{12}$

$4^{3}\times 4^{21}=4^{3+21}=4^{24}$

Exercice 17

Recopions et complétons chacune des égalités ci-dessous par une puissance d'un nombre décimal :

On rappelle que si $a$ est un nombre décimal, $m\ $ et $n\ $ deux entiers naturels alors, on a :

$$(a^{m})^{n}=a^{m\times n}$$

En appliquant cette propriété de la puissance dans $\mathbb{D}$, on obtient :

$(14.3^{2})^{5}=(14.3)^{2\times 5}=(14.3)^{10}$

$(0.4^{7})^{5}=(0.4)^{7\times 5}=(0.4)^{35}$

$(2^{5})^{1}=2^{5\times 1}=2^{5}$

$(11^{7})^{5}=11^{7\times 5}=11^{35}$

Exercice 18

Mon camarade de classe a effectué les calculs ci-dessous :

a) $4^{2}=2^{4}$

b) $2^{5}=32$

c) $(7\times 5)^{6}=7^{6}\times 5^{6}$

d) $2\times 7^{3}=(2\times 7)^{3}$

e) $2\times 3^{2}=36$

f) $(11^{7})^{5}=11^{12}$

Recopions les égalités fausses et corrigeons-les.

d) $2^{3}\times 7^{3}=(2\times 7)^{3}$

e) $(2\times 3)^{2}=36$

f) $(11^{7})^{5}=11^{35}$

Exercice 19

Recopions et complétons les égalités ci-dessous :

a) $3\times 3\times 3\times 3\times 3\times 3=3^{6}$

b) $7\times 7\times 7\times 2\times 2\times 2\times 2=2^{4}\times 7^{3}$

c) $4\times 4\times 4\times 4\times 4\times 4=4^{6}=(2^{2})^{6}$

d) $10\times 10\times 10\times 10\times 10=(2\times 5)^{5}$

e) $(2\times 3)^{5}=2\times 2\times 2\times 2\times 2\times 3\times 3\times 3\times 3\times 3$

f) $(2\times 3)^{5}=2^{5}\times 3^{5}$

Exercice 20

1) Citons tous les nombres plus petits que $20$ qui s'écrivent sous la forme $2^{n}$ avec $n$ un entier naturel supérieur ou égal à $1.$

$$2\;;\ 4\;;\ 8\;;\ 16$$

En les mettant sous la forme $2^{n}$ on trouve :

$$2^{1}\;;\ 2^{2}\;;\ 2^{3}\;;\ 2^{4}$$

2) Citons tous les nombres plus petits que $35$ qui s'écrivent sous la forme $3^{n}$ avec $n$ un entier naturel supérieur ou égal à $1.$

$$3\;;\ 9\;;\ 27$$

En les mettant sous la forme $3^{n}$ on obtient :

$$3^{1}\;;\ 3^{2}\;;\ 3^{3}$$

Exercice 21

Un commerçant possède $5$ caisses contenant chacune $5$ cartons ; chaque carton contient $5$ paquets ; chaque paquet contient $5$ objets. Déterminons le nombre total d'objets que le commerçant possède.

Comme chaque caisse contient $5$ cartons alors, le nombre total de cartons est donné par :

$\begin{array}{rcl}\text{nombre total de cartons}&=&\text{nombre total de caisses}\times 5\\\\&=&5\times 5\\\\&=&5^{2}\end{array}$

Ensuite, comme chaque carton contient $5$ paquets alors, le nombre total de paquets est donné par :

$\begin{array}{rcl}\text{nombre total de paquets}&=&\text{nombre total de cartons}\times 5\\\\&=&5^{2}\times 5\\\\&=&5^{3}\end{array}$

Enfin, comme chaque paquet contient $5$ objets alors, le nombre total d'objets est donné par :

$\begin{array}{rcl}\text{nombre total d'objets}&=&\text{nombre total de paquets}\times 5\\\\&=&5^{3}\times 5\\\\&=&5^{4}\end{array}$

En calculant, on trouve : $5^{4}=625$

Ainsi, le commerçant possède au total $625$ objets.

Exercice 22

1) a) Calculons le carré du double de $6.$

Le double de $6$ est égal à : $2\times 6$

$\begin{array}{rcl}\text{Alors, le carré du double de }6&=&(2\times 6)^{2}\\\\&=&12^{2}\\\\&=&144\end{array}$

Donc, le carré du double de $6$ est égal à : $144$

b) Calculons le double du carré de $6.$

Le carré de $6$ est égal à : $6^{2}$

$\begin{array}{rcl}\text{Alors, le double du carré de }6&=&2\times 6^{2}\\\\&=&2\times 36\\\\&=&72\end{array}$

Donc, le double du carré de $6$ est égal à : $72$

2) a) Calculons le triple du cube de $4.$

Le cube de $4$ est égal à : $4^{3}$

$\begin{array}{rcl}\text{Alors, le triple du cube de }4&=&3\times 4^{3}\\\\&=&3\times 64\\\\&=&192\end{array}$

Donc, le triple du cube de $4$ est égal à : $192$

b) Calculons le cube du triple de $4.$

Le triple de $4$ est égal à : $3\times 4$

$\begin{array}{rcl}\text{Alors, le cube du triple de }4&=&(3\times 4)^{3}\\\\&=&12^{3}\\\\&=&1\,728\end{array}$

Donc, le cube du triple de $4$ est égal à : $1\,728$

Exercice 23

1) Montrons que : $4a^{2}\times 25b^{2}=(10ab)^{2}$

On a : $4a^{2}\times 25b^{2}=4\times a^{2}\times 25\times b^{2}$

Or, on sait que : $4=2^{2}\ $ et $\ 25=5^{2}$

Remplaçons alors $4\ $ et $\ 25$ par $2^{2}\ $ et $\ 5^{2}.$

On obtient :

$\begin{array}{rcl}4a^{2}\times 25b^{2}&=&4\times a^{2}\times 25\times b^{2}\\\\&=&2^{2}\times a^{2}\times 5^{2}\times b^{2}\\\\&=&(2\times a\times 5\times b)^{3}\\\\&=&(2\times 5\times a\times b)^{2}\\\\&=&(10\times a\times b)^{2}\end{array}$

Ce qui montre que : $4a^{2}\times 25b^{2}=(10ab)^{2}$

2) Montrons que : $8a^{3}\times 27b^{3}=(6ab)^{3}$

On a : $8=2^{3}\ $ et $\ 27=3^{3}$

Donc, en remplaçant $8\ $ et $\ 27$ par $2^{3}\ $ et $\ 3^{3}$, on obtient :

$\begin{array}{rcl}8a^{3}\times 27b^{3}&=&8\times a^{3}\times 27\times b^{3}\\\\&=&2^{3}\times a^{3}\times 3^{3}\times b^{3}\\\\&=&(2\times a\times 3\times b)^{3}\\\\&=&(2\times 3\times a\times b)^{2}\\\\&=&(6\times a\times b)^{3}\end{array}$

D'où, $8a^{3}\times 27b^{3}=(6ab)^{3}$

Auteur:

Diny Faye & Lassana Diakhaté