Statistique - 4e
Classe:
Quatrième
La statistique est une branche des mathématiques qui a pour objectif de recueillir, de classer, de réduire puis de traiter et d'analyser des données afin d'en faire une déduction (établir des prévisions).
I. Vocabulaires et exemples
Activité :
Considérons le village de Keur Moussa.
1) Comment appelle-t-on les hommes et les femmes qui habitent Keur Moussa ?
2) Combien de quartiers y-a-t-il dans Keur Moussa ?
3) Quelles sont les différences entre les habitants de Keur Moussa ?
4) Quelle est le nombre d'hommes ? de femmes ?
5) Quelles sont les ethnies représentées?
Solution :
1) Ils représentent la population de Keur Moussa
2) Il y a 8 quartiers : ndiayène, payène, ndiobènetaye, ASC(babilone), diamaguène, ndiakhate, ndiagne, tianaba,(échantillon)
3) a) Taille, poids, age,(caractère quantitatif)
b) Ethnies, sexe, religion,(caractère qualitatif)
4) Hommes=17638, femmes=24167 (caractère quantitatif)
5) Les ethnies représentées sont:
I.1 Population
L'ensemble sur lequel on recueille les données est appelé population.
La population a des propriétés appelées caractères.
I.2 Échantillon
Un échantillon est un sous ensemble de la population.
Remarque :
Lorsque l'effectif de l'échantillon est $n$, on dit qu'on a un échantillon de taille $n$.
I.3 Individu
Tout élément de la population est appelé individu.
I.4 Caractère
Un caractère est toute information qu'on peut étudier sur la population.
Exemple 1 :
Considérons l'ensemble des élèves d'une classe.
L'ensemble des élèves de la classe est une population.
Chaque élève de la classe est un individu.
Un sous ensemble d'élèves de la classe forme un échantillon.
Sur cette population, on peut étudier les caractères : ages, taille, race, ethnie, poids, nationalité, notes
Exemple 2 :
Considérons l'ensemble des entreprises du Sénégal en $2002.$
L'ensemble de ces entreprises est une population.
Chaque entreprise est un individu.
Un sous ensemble d'entreprise forme un échantillon
Sur cette population d'entreprises, on peut étudier les caractères : nombre d'employés, chiffre d'affaires de l'année $2000$, salaire des employés
Remarque 1
Un caractère est quantitatif ou qualitatif
Un caractère est quantitatif, lorsqu'il peut être exprimé par un nombre (par mesure comptage).
Exemple :
Sur une population d'étudiants, les caractères : nationalité, race, ethnie, et situation matrimoniale sont qualitatifs.
Remarque 2
Un caractère quantitatif est discret ou continu.
Un caractère est discret lorsqu'il est susceptible de prendre toutes les valeurs d'un intervalle.
Exemple :
Sur une population d'étudiants, le caractère taille est continu. Par contre le caractère nationalité est discret.
I.5 Variables
La variable ou la série statistique est toutes les valeurs prises par les modalités.
II. Classement des données statistiques
II.1 Séries statistiques brutes
Voici la taille des élèves d'une classe de $4^{e}$ :
$$\begin{array}{cccccc} 150&145&150&160&155&155 \\ 175&175&150&170&165&155 \\ 150&160&175&170&160&170 \\ 150&165&170& & & \end{array}$$
II.2 Séries statistiques ordonnées
$$\begin{array}{|c|c|c|c|c|c|c|c|}\hline\text{Taille des élèves en }cm & 145 & 150 & 155 & 160 & 165 & 170 & 175 \\ \hline\text{Effectifs} & & & & & & & \\ \hline\end{array}$$
II.2.1 Modalité
La modalité est toute valeur possible d'un caractère étudié.
Exemple 1 :
Sur une population d'étudiants, les modalités du caractère mention obtenue au bac sont : Passable, Assez Bien, Bien, Très Bien.
Exemple 2 :
Considérons une population formée de quatre enfants d'une même famille, âgés respectivement de 12 ; 8 ; 3 et 1 ans.
Chacune de ces valeurs est une modalité du caractère age.
Remarque
Dans le cas d'un caractère continu, les modalités sont appelées des classes.
Une classe est un intervalle du type $[a\;;\ b[$, il est obtenu par regroupement des valeurs du caractère.
On admet que le centre d'une classe $[a\;;\ b[$ est $c=\dfrac{a+b}{2}$ et l'amplitude est égale à $b-a.$
II.2.2 Effectif
L'effectif d'une modalité M, le nombre d'individus pour lesquels le caractère prend la valeur M.
L'effectif d'une classe, le nombre d'individus pour lesquels le caractère prend une valeur appartenant à cette classe.
L'effectif partiel est le nombre d'individus d'une modalité.
L'effectif total est le nombre d'individu de la population ou la somme des effectifs partiels. On la note $N.$
II.2.3 Mode
Le mode d'un caractère est la modalité qui a l'effectif le plus élevé. C'est la valeur qui a la plus grande fréquence.
Dans le cas où les modalités sont des classes, on parle de classe modale et on prend comme mode le centre de cette classe modale.
Remarque
Le mode est facile à déterminer et d'interprétation rapide, mais il n'est pas souvent unique et n'existe même pas parfois.
II.2.4 Moyenne
Soit $X$ une variable discrète dont les modalités notées dans l'ordre croissant $x_{1}\;,\ x_{2}\;,\ x_{3}\;,\ \cdots\;,\ x_{P}$ sont d'effectifs respectifs $n_{1}\;,\ n_{2}\;,\ n_{3}\;,\ \cdots\;,\ n_{p}$ et de fréquences respectives $f_{1}\;,\ f_{2}\;,\ f_{3}\;,\ \cdots\;,\ f_{p}.$
La moyenne arithmétique de cette série est le réel noté en général $\overline{x}$ et défini par la formule $$\overline{x}=\dfrac{1}{N}\sum_{i=1}^{p}n_{i}x_{i}=\sum_{i=1}^{p}f_{i}x_{i}$$
Dans le cas où les modalités sont des classes : $$\overline{x}=\dfrac{1}{N}\sum_{i=1}^{p}c_{i}n_{i}$$
où les $c_{i}$ sont les centres des classes.
La moyenne est la valeur autour de laquelle tournent toutes les valeurs de la série.
Disposition pratique pour le calcul de la moyenne
$$\begin{array}{|c|c|c|c|c|c|c|}\hline x_{i} & 4 & 5 & 6 & 7 & 9 & \text{Total} \\ \hline n_{i} & 15 & 5 & 5 & 10 & 20 & 55 \\ \hline n_{i}x_{i} & 60 & 25 & 30 & 70 & 180 & 360 \\ \hline \end{array}\qquad \overline{x}=\dfrac{360}{55}=\dfrac{72}{11}$$
II.2.5 Fréquence
Soit $N$ l'effectif total d'une population.
Si $n_{i}$ représente l'effectif d'une modalité $M_{i}$ alors la fréquence de cette classe est $f_{i}=\dfrac{n_{i}}{N}$ ou $f_{i}=\dfrac{100\times n_{i}}{N}\%$ lorsqu'elle est exprimée en pourcentage.
Soit $N$ l'effectif total d'une population.
Si $n_{i}$ représente l'effectif d'une classe $[a_{i}\;;\ b_{i}[$ alors la fréquence de cette classe est $f_{i}=\dfrac{n_{i}}{N}$ ou $f_{i}=\dfrac{100\times n_{i}}{N}\%$ lorsqu'elle est exprimée en pourcentage.
Remarque :
La somme des fréquences est égale à 1.
II.2.6 Pourcentage
Exercice d'application :
On a relevé les tailles en cm de 40 élèves d'une classe de $4^{e}$ :
$$\begin{array}{cccccccc} 161&152&159&168&164&168&153&146 \\ 155&155&163&160&155&160&160&170 \\ 160&180&146&155&159&172&164&160 \\ 155&159&159&158&161&164&152&176 \\ 163&159&155&149&182&155&165&152\end{array}$$
1) Quelle est la population étudiée?
2) Quels sont les individus ?
3)Donne un échantillon de la population.
4)Quel est l'effectif de la population
5) Présente dans un tableau les modalités, les effectifs,les fréquences et les pourcentages.
6) Calcule la taille moyenne des élèves de cette classe.
7) Donne le mode de la série
III. Représentations graphiques
Voici la répartition des groupes ethniques à l'intérieur d'une population.
$$\begin{array}{|c|c|c|c|c|c|c|c|}\hline\text{Groupes}&\text{Sarakolé}&\text{Sérère}&\text{Socé}&\text{Toucouleur}&\text{Wolof}&\text{Maure}&\text{TOTAL} \\ \text{ethniques} & & & & & & & \\ \hline\text{Effectifs}&130&370&160&600&900&110& \\ \hline\text{Fréquences} & & & & & & & \\ \hline\text{Pourcentages} & & & & & & & \\ \hline\text{Angles} & & & & & & & \\ \text{du diagramme} & & & & & & & \\ \text{circulaire} & & & & & & & \\ \hline\text{Angles} & & & & & & & \\ \text{du diagramme} & & & & & & & \\ \text{semi-circulaire} & & & & & & & \\ \hline\end{array}$$
1) Complète le tableau.
2) Représente les diagrammes en bâtons, en bandes, circulaire et semi-circulaire
III.1 Diagramme en bâtons
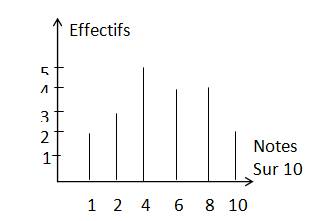
III.2 Diagramme en bandes
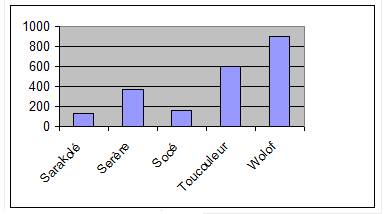
III.3 Diagramme circulaire
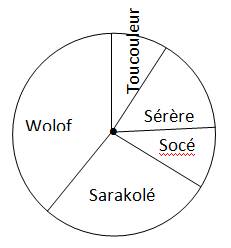
III.4 Diagramme semi-circulaire
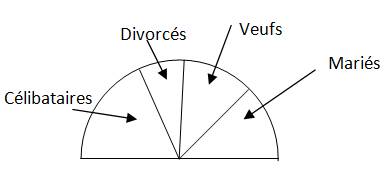
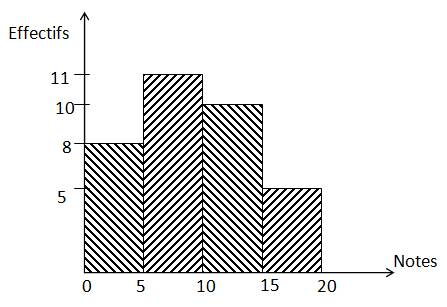
III.5 Histogramme

Commentaires
Tyma gangue (non vérifié)
sam, 06/26/2021 - 01:41
Permalien
Il faut y insérer anglais
Anonyme (non vérifié)
mar, 04/22/2025 - 22:50
Permalien
J'aime votre facon de penser
Ajouter un commentaire