Statistique - TL
Classe:
Terminale
I. Introduction
De manière brève voici rappelé le vocabulaire élémentaire de la statistique
Population :
On appelle population l'ensemble sur lequel porte l'étude menée.
Une population peut être constituée de personnes, d'animaux, d'objets, etc.
Individu :
Tout élément d'une population est appelé individu.
Échantillon :
On appelle échantillon toute partie non vide de la population.
Exemple :
Dans les démocraties mûres, à la veille de la tenue des élections les statisticiens font des sondages portant sur un échantillon de la population électorale pour déterminer les tendances.
Caractère :
C'est toute propriété étudiée sur une population ou l'échantillon.
Sur une population, on peut étudier un ou plusieurs caractères.
Il existe deux types de caractères.
$-\ $Les caractères qualitatifs :
Qui ne s'expriment pas par un nombre réel.
Exemple :
Le groupe sanguin, le sexe, la nationalité,$\ldots$
$-\ $Les caractères qualitatifs :
Qui s'expriment par un nombre réel.
Exemple :
la taille, le poids, l'âge,$\ldots$
II. Séries statistiques doubles
$-\ $Si on étudie un caractère $X$ sur une population, l'ensemble noté $\left(X_{1}\right)$ des valeurs prises par le caractère est dit série statistique simple (ou à une variable).
$-\ $Il arrive qu'on étudie simultanément deux caractères $X$ et sur les individus d'une population donnée.
Dans ce cas, l'ensemble des coupes de valeurs $\left(X_{i}\;,\ Y_{i}\right)$ est appelé série statistique double.
Exemple :
Sur une classe de terminale, on peut étudier simultanément
1. Nuage de points
N.B.
Dans toute la suite, on travaillera sur l'exemple $\left(^{\ast}\right)$ ci-après :
Exemple :
$\left(^{\ast}\right)$ : Voici le relevé de deux caractères étudiés sur une même population.
$$\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline X_{i}&9.6&12.8&18.4&31.2&36.8&47.2&49.6&56.8\\ \hline Y_{1}&70&86&90&104&120&128&144&154\\ \hline \end{array}$$
Dans le plan muni d'un repère orthogonal $(O\;,\ \vec{i}\;,\ \vec{j})$ l'ensemble des points $M_{i}\left(x_{i}\;,\ y_{i}\right)$ est appelé nuage de points.
Exercice d'application :
Représenter le nuage de points de la série double définie par le tableau ci-dessus.
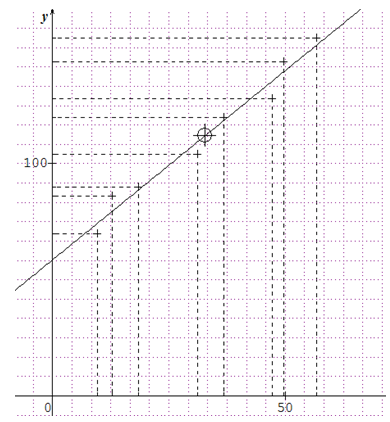
2. Moyennes de $X$ et de $Y$
L'effectif total noté $N$ est égal au nombre d'individus de la population.
Dans l'exemple $N=8$
$-\ $La moyenne de $X$ est noté $\overline{X}$ et on a :
$$\boxed{\overline{X}=\dfrac{x_{1}+x_{2}+\ldots+x_{n}}{N}=\dfrac{1}{n}\sum\limits_{i=1}^{n}x_{i}}$$
$-\ $La moyenne de $Y$ est noté $\overline{Y}$ et on a :
$$\boxed{\overline{Y}=\dfrac{y_{1}+y_{2}+\ldots+y_{n}}{N}=\dfrac{1}{n}=\sum\limits_{i=1}^{n}y_{i}}$$
Exercice d'application :
Dans l'exemple, calculer $\overline{X}$ et $\overline{Y}$
Réponse :
$\overline{X}=32.8$ et $\overline{Y}=112$
3. Point moyen du nuage
Le point moyen du nuage est le point $G\left(\overline{X}\;,\ \overline{Y}\right).$
Dans l'exemple $\left(^{\ast}\right)$ $G(32.8\ ;\ 112)$
4. Variances et écart-types de $X$ et $Y$
La variance de $X$ est de réel noté $V(X)$ et vaut :
$$\boxed{V(X)=\dfrac{x_{1}^{2}+x_{2}^{2}+\ldots+x_{n}^{2}}{n}-\overline{X}=\dfrac{1}{n}\sum\limits_{1}^{n}x_{i}^{n}-\overline{X}}$$
L'écart-type de $X$ est noté $\sigma(X)$ et on a : $\sigma(X)=\sqrt{V(X)}$
On définit de même la variance et l'écart-type de $Y.$
Exercice d'application :
Dans l'exemple $\left(^{\ast}\right)$, calculer la covariance $X$ et $Y$
Réponse :
$\sigma(X)=16.7\ ;\ \sum(Y)=27.60$
5. Covariance de $X$ et $Y$
La covariance de $X$ et $Y$ est le réel noté $cov(X\;,\ Y)$ ou $\sum_{XY}$ défini par :
$$cov(X\;,\ Y)=\dfrac{x_{1}y_{1}+x_{2}y_{2}+\ldots+x_{n}y_{n}}{N}-\overline{X}\overline{Y}=\dfrac{1}{N}\sum\limits_{i=1}^{n}X_{i}Y_{i}-\overline{X}\overline{Y}.$$
Exercice d'application :
Dans l'exemple $\left({\ast}\right)$, calculer la covariance de $x$ et $y.$
Réponse :
$cov(x\;,\ y)=454$
6. Coefficient de corrélation linéaire
On appelle coefficient de corrélation linéaire le réel noté $r(X\;,\ Y)$ défini par :
$$r(X\;,\ Y)=\dfrac{cov(X\;,\ Y}{\sum(X)\sigma(Y)}$$
Exercice d'application :
Dans l'exemple $\left(^{\ast}\right)$, calculer $r(X\;,\ Y)$
Réponse :
$r(X\;,\ Y)=0.985$
N.B :
$r(X\;,\ Y)$ est toujours compris entre $-1$ et $1.$
Plus il est proche de $1$ $($ou de $-1)$, plus on estime qu'il y a une bonne corrélation entre $X$ et $Y.$
III. Ajustement linéaire
Ajuster de manière linéaire un nuage, c'est trouver une droite passant le plus près de tous les points du nuage.
On peut ajuster de plusieurs façons un nuage.
Ajustement par la méthode des moindres carrés : Droites de régression
Ici la droite cherchée s'appelle droite de régression (ou droite d'estimation).
a. droite de régression de $Y$ en $X$
La droite de régression de $Y$ en $X$ est noté $D_{y/x}.$
Son équation est :
$y-\overline{Y}=\alpha\left(x-\overline{X}\right)\text{ avec }\alpha=\dfrac{cov(X\;,\ Y)}{V(Y)}$
b. droite de régression de $X$ en $Y$
La droite régression de $X$ en $Y$ est notée $D_{x/y}.$
Son équation est :
$x-\overline{X}=\alpha^{\prime}\left(x-\overline{X}\right)$ avec $\alpha^{\prime}=\dfrac{cov(X\,;\ Y)}{V(Y)}$
Remarque :
Les droites de régression de $Y$ en $X$ et de $X$ en $Y$ passant toutes deux par le point moyen du nuage.
Exercice d'application :
Dans l'exemple $\left(^{\ast}\right)$, donner équation de $D_{x/y}.$
Réponse :
$V(X)=278.89$ et $V(Y)=761.76$
Donc $D_{y/x}\ :\ x-32.8=\alpha^{\prime}(y-112)\text{ avec }\alpha^{\prime}=\dfrac{454}{761.76}=0.59$
$\Rightarrow\;x=0.59y-33.28.$

Commentaires
Anonyme (non vérifié)
ven, 02/14/2025 - 12:44
Permalien
c intéressant
Ajouter un commentaire