Suites numériques - 1er S
Classe:
Première
Notion de suite numérique
Il arrive que l'on demande, lors de tests psychotechniques par exemple, de compléter ''logiquement'' une suite de nombres
Exemple 1 :
$1$, $2$, $4$, $8$, $16$, $32$, $64$, $128$, $\ldots$
$1$, $4$, $9$, $16$, $25$, $36$, $49$, $64$, $\ldots$
$-3$, $1$, $5$, $9$, $13$, $17$, $21$, $25$, $\ldots$
$1$, $1$, $2$, $3$, $5$, $8$, $13$, $21$, $34$, $\ldots$
En mathématiques, une suite $u$ est une liste ordonnée de nombres réels :
Les éléments de cette liste sont appelés termes de la suite $u$, et sont tous repérés par leur rang dans la liste ; ainsi le premier terme est souvent noté $u_{0}$, le second $u_{1}$ et ainsi de suite $\ldots$
I. Définition
On appelle suite numérique réelle une fonction $U$ d'une partie $A$ de $\mathbb{N}$ vers $\mathbb{R}$
\begin{eqnarray} U\ :\ A\subset\mathbb{N} &\rightarrow & \mathbb{R}\nonumber\\ n &\rightarrow & U(n)\nonumber \end{eqnarray}
Le mot suite désigne donc toute fonction dont l'ensemble de départ est inclus dans l'ensemble $\mathbb{N}$ des entiers naturels.
N.B.
Le plus souvent, $A=\mathbb{N}$ ou $A=\mathbb{N}^{\ast}.$
On a l'habitude de noter les fonctions numériques par $f$, $g$, $h$, etc ... , mais pour les suites, on utilise plutôt les lettres $u$, $v$, $w$, ...
Exemples :
La fonction $U$ définie sur $\mathbb{N}$ par :
$U(n)=n^{2}+n+1$ est une suite numérique réelle
La fonction $V$ définie sur $\mathbb{N}^{\ast}$ par $V(n)=\dfrac{1}{n}$ est une suite numérique réelle
II. Notion d'indice-Notation indicielle
1) Terme d'indice $n$ ou terme général :
$U$ étant une suite numérique réelle, $U(n)$ est appelé terme d'indice $n$ de cette suite $U$ et on note $U(n)=U_{n}$
$U_{n}$ se lit « $U$ indice $n$ » est appelé terme général de la suite $U$
Exemple :
Soit la suite $U$ : $\mathbb{N}\longrightarrow\mathbb{R}$ telle que $U(n)=\sqrt{n^{2}+n+1}$
Le terme d'indice $0$ de cette suite est $U_{0}=\sqrt{1}=1$
Le terme d'indice $1$ est $U_{1}=\sqrt{3}$
Le terme d'indice $n-1$ s'obtient en remplaçant, dans l'expression de $U(n)$, $n$ par $n-1$ :
$U(n-1)=\sqrt{(n-1)^{2}+(n-1)+1}=\sqrt{n^{2}-n+1}$
Le terme $n+1$ est $U_{n+1})=\sqrt{(n+1)^{2}+(n+1)+1}=\sqrt{n^{2}+3n+3}$
Les termes de cette suite sont : $U_{0}$, $U_{1}$, $U_{3}$, $U_{4}$, $\ldots$, $U_{n-1}$, $U_{n}$, $U_{n+1}$, $\ldots$, $U_{2n-1}$, $U_{2n}$, $U_{2n+1}$, $\ldots$
Remarques :
Soit $U$ une suite numérique réelle.
L'ensemble de définitions $I$ de cette fonction $U$ de $\mathbb{N}$ vers $\mathbb{R}$, coïncide avec l'ensemble des indices des termes de cette suite.
Dans ce cas, la suite $U$ est notée $\left(U_{n}\right)n\in I$ et $U_{n}$ qui est un des termes de cette suite.
Remarque :
Ne pas confondre :
$\cdot\ \ $ la suite $(u_{n})$ qui est une application ;
$\cdot\ \ $ le terme de rang $n$, $u_{n}$ qui est un réel ;
$\cdot\ \ \{u_{n}\;,\ n\in\mathbb{N}\}$, ensemble des valeurs de la suite
III. Modes de génération des termes d'une suite
1) Mode explicite :
Lorsque $U_{n}$ est donné en fonction de $n$ , alors on dit que la suite $\left(U_{n}\right)$ est définie de façon explicite.
Exemple :
La suite $\left(U_{n}\right)n\in I\setminus\{0\;,\ 1\}$ telle que $U_{n}=\sqrt{n-2}$, est définie de façon explicite
L'ensemble des indices de cette suite est $\mathbb{N}\setminus\{0\;,\ 1\}=\{2\;,\ 3\;,\ 4\;,\ldots\}$
2) Suite récurrente :
On peut définir une suite en donnant certains de ses premiers termes généraux $U_{n-1}$, $U_{n}$, $U_{n+1}$, $\ldots$ on dit alors que la suite $\left(U_{n}\right)$ est une suite récurrente
Exemple 1 :
Considérons la suite $\left(U_{n}\right)$ telle que $\left(U_{0}\right)=4$ et pour tout entier naturel $n$, $U_{n+1}=3U_{n}+7$
$\left(U_{n}\right)$ est une suite récurrente définie par la donnée de son premier terme $\left(U_{0}\right)$ et la relation $U_{n+1}=3U_{n}+7$ appelée relation de récurrence.
Un terme d'une telle suite ne peut être déterminé que si le terme précédent est connu.
$U_{1}=3U_{0}+7=3\times 2+7=13$
$U_{2}=3U_{1}+7=3\times 13+7=46$
$U_{3}=3U_{2}+7=3\times 49+7=154$
................................
................................
................................
................................
Exemple 2 :
Considérons la suite $(\mathfrak{t})$ telle que :
$\mathfrak{t}_{1}=1$, $\mathfrak{t}_{2}=-3$ , et pour tout $n\in\mathbb{N}^{\ast}$, $\mathfrak{t}_{n+1}=\dfrac{2}{3}\mathfrak{t}_{n}+\mathfrak{t}_{n-1}$
$\mathfrak{t}_{3}=\dfrac{2}{3}\mathfrak{t}_{2}+\mathfrak{t}_{1}=-1,$ $\ldots$
IV. Opérations sur les suites
Dans l'ensemble des suites définies sur une même partie non vide $I$ de $\mathbb{N}$, on peut définir des opérateurs tels qu'addition, soustraction, inverse, multiplication, quotient
Soient $\left(U_{n}\right)n\in I$ et $\left(V_{n}\right)n\in I$ deux suites
$-\ \ $ La somme des suites $\left(U_{n}\right)n\in I$ et $\left(V_{n}\right)n\in I$ est la suite $\left(U_{n}+V_{n}\right)n\in I$ de terme général $U_{n}+V_{n}.$
$-\ \ $ Le produit des suites $\left(U_{n}\right)n\in I$ et $\left(V_{n}\right)n\in I$ est la suite $\left(U_{n}V_{n}\right)n\in I$ de terme général $U_{n}V_{n}.$
$-\ \ $ Si $U_{n}\neq 0$, pour tout $n\in I$, la suite inverse de la suite $\left(U_{n}\right)$ est la suite $\left(\dfrac{1}{U_{n}}\right)n\in I$ de terme général $U_{n}+V_{n}.$
$-\ \ $ Si $V_{n}\neq 0$, pour tout $n\in I$, le quotient des suites $\left(U_{n}\right)n\in I$ et $\left(V_{n}\right)n\in I$ est la suite $\left(\dfrac{U_{n}}{V_{n}}\right)n\in I$ de terme général $\dfrac{U_{n}}{V_{n}}$
V. Monotonie ou sens de variation d'une suite :
1) Suite croissante :
Une suite $\left(U_{n}\right)n\in I$ est croissante si et seulement si
$\forall\,n\in I\;,\ bU_{n}\leq U_{n+1}\text{ ou }U_{n+1}-U_{n}\geq 0$
Exemple :
Soit la suite $\left(U_{n}\right)$ définie par :
$\forall\,n\in\mathbb{N}\;,\ U_{n}=\dfrac{n^{2}-n+2}{2}$
$\forall\,n\in\mathbb{N}\;,\ U_{n+1}-U_{n}=\dfrac{(n+1)^{2}-(n+1)+2}{2}-\dfrac{n^{2}-n+2}{2}=n$
donc pour tout $n\in\mathbb{N}$, $U_{n+1}-U_{n}\geq 0$ ; la suite $\left(U_{n}\right)$ est alors une suite croissante cela peut se traduire par :
$U_{0}\leq U_{1}\leq U_{3}\leq U_{4}\leq\ldots\leq U_{n-1}\leq U_{n}\leq U_{n+1}\leq\ldots$
Remarque :
Une suite $\left(U_{n}\right)n\in I$ est strictement croissante si et seulement si
$\forall\,n\in I\;,\ U_{n+1}-U_{n}>0$ ou $U_{n}<U_{n+1}$
2) Suite décroissante
Une suite $\left(U_{n}\right)n\in I$ est décroissante si et seulement si :
$\forall\,n\in I\;,\ U_{n+1}-U_{n}\leq 0$ ou $U_{n}\geq U_{n+1}$
Exemple :
Soit la suite $\left(U_{n}\right)$ définie par :
$\forall\,n\in\mathbb{N}\;,\ U_{n}=-n^{2}+n-2$
$\forall\,n\in\mathbb{N}\;,\ U_{n+1}-U_{n}=-2n\;;\text{ donc }\forall\,n\in\mathbb{N}\;,\ U_{n+1}-U_{n}\leq 0$
La suite $\left(U_{n}\right)n\in\mathbb{N}$ est alors décroissante ; ce qui équivaut à
$$U_{0}\geq U_{1}\geq U_{2}\geq\cdots\geq U_{n}\geq\ldots$$
Remarque :
Une suite $\left(U_{n}\right)n\in I$ est strictement décroissante si et seulement si :
$\forall\,n\in I\;,\ U_{n+1}-U_{n}<0\text{ ou }U_{n}<U_{n+1}$
3) Monotonie d'une suite
Une suite est dite monotone lorsqu'elle est ou bien croissante ou bien décroissante.
Une suite est dite strictement monotone lorsqu'elle est ou bien strictement croissante ou bien strictement décroissante.
Remarque :
cas d'une suite strictement positive ou bien strictement négative
Une suite $\left(U_{n}\right)n\in I$ est dite positive, lorsque, $\forall\,n\in I\;,\ U_{n}\geq 0$
Une suite $\left(U_{n}\right)n\in I$ est dite strictement positive, lorsque, $\forall\,n\in I\;,\ U_{n}>0$
Une suite $\left(U_{n}\right)n\in I$ est dite négative, lorsque, $\forall\,n\in I\;,\ U_{n}\leq 0$
Une suite $\left(U_{n}\right)n\in I$ est dite strictement négative lorsque, $\forall\,n\in I\;,\ U_{n}<0$
VI. Méthode de raisonnement par récurrence
Exemple 1 :
Soit à démontrer la propriété :
$(1)\quad 1^{2}+2^{2}+3^{2}+\ldots+n^{2}=\dfrac{n(n+1)(2n+1)}{6}\forall\,n\in\mathbb{N}^{\ast}$,
a) Remarquons d'abord que cette propriété est vraie pour $n=1$, car alors le membre de gauche est égal à $1^{2}=1$ et celui de droite à $\dfrac{1\times 2\times 3}{6}=1.$
b) Supposons que la propriété est vraie pour un entier $k$, c'est-à-dire que :
$(2)\quad 1^{2}+2^{2}+3^{2}+\ldots+k^{2}=\dfrac{k(k+1)(2k+1)}{6}.$
Montrons alors qu'elle est vraie pour $n=k+1.$
En effet, d'après $(2)$ :
$\begin{array}{rcl} 1^{2}+2^{2}+3^{2}+\ldots+k^{2}+(k+1)^{2}&=&\dfrac{k(k+1)(2k+1)}{6}+(k+1)^{2}\\ \\&=&(k+1)\left(\dfrac{k(2k+1)}{6}+(k+1)\right)\\ \\&=&(k+1)\left(\dfrac{2k^{2}+7k+6}{6}\right)\\ \\&=&\dfrac{(k+1)(k+2)(2k+3)}{6}\quad(3)\end{array}$
$(3)$ est identique à $(1)$ avec $n=k+1.$
Ainsi, on a démontré que :
$(3)$ Si la propriété est vraie pour $n=k$, alors elle est vraie pour $n=k+1.$
c) Or $(1)$ est vraie pour $n=1$, donc d'après $(3)$ avec $n=1$ , elle est vraie pour $n=2.$
Donc, d'après $(3)$ avec $n=2$, elle est vraie pour $n=3.$
Donc, d'après $(3)$ avec $n=3$, elle est vraie pour $n=4\ldots$
En continuant ce raisonnement, on voit que la propriété $(1)$ est vraie pour tout entier naturel $n.$
De manière générale, nous admettrons le principe suivant, appelé principe de récurrence :
Soit à démontrer une propriété $(P_{n})$ dépendant de l'entier naturel $n.$
(a) Si on démontre qu'elle est vraie pour une certaine valeur $n=n_{0}$,
(b) Et si on démontre que dès qu'elle est vraie pour $n=k$, alors elle est vraie pour $n=k+1$
(c) Alors, on peut conclure qu'elle est vraie pour $n\geq n_{0}.$
Exemple 2 :
Démontrer que :
$\forall\,\geq 1\;,\ 7\text{ divise }2^{n+1}+3^{2n-1}.$
N.B.
On dit que l'entier $k$ divise l'entier $n$ (notation : $k|n$) si et seulement si :
Il existe un entier $p$ tel que : $n=k\times p.$
(a) pour $n=1\;,\ 2^{2}+3^{1}=7=7\times 1\text{ et }7|7$ , donc la propriété est vraie.
(b) Supposons qu'elle est vraie pour $n=k$, c'est-à-dire que : $7|2^{k+1}+3^{2k-1}.$
Il existe donc un entier $p$ tel que $2^{k+1}+3^{2k-1}=7p\quad (\ast).$
Alors, $2^{k+2}+3^{2k+1}=2\left(2^{k+1}\right)+ 9\times 3^{2k-1}.$
D'après $(\ast)$, ceci est égal à :
$2\left(7p-3^{2k-1}\right)+9\times 3^{2k-1}=14p+7\times 3^{2k-1}=7\left(2p+3^{2k-1}\right).$
Donc, $2^{k+2}+3^{2k+1}$ est aussi un multiple de $7.$
On en conclut que :
$\forall\,n\geq 1\;,\ 7\text{ divise }2^{n+1}+3^{2n-1}.$
VII. Suites périodiques
Définition
Soit $p$ un entier naturel non nul.
On dit que la suite $(u_{n}n\in A$ est périodique de période $p$ si, pour tout $n$ de $A$, on a : $u_{n+p}=u_{n}.$
Exemple :
Soit $(u_{n})$ la suite définie sur $\mathbb{N}$ par $u_{n}=(-1)^{n}.$
Pour tout entier naturel $n$, on a $u_{n+2}=u_{n}.$
Cette suite est donc périodique, de période $2.$
Exercices
1) Montrer que les suites $(u_{n})$ et $(v_{n})$ suivantes sont périodiques et déterminer leur période.
a) $u_{n}=\sin\dfrac{n\pi}{2}$
b) $v_{n}=\tan\dfrac{n\pi}{3}$
c) $u_{n}=\cos\dfrac{n\pi}{7}$
d) $u_{n}=(-1)^{n}\cos\dfrac{3n\pi}{7}.$
2) Soit $p$ un entier strictement positif fixé, $E$ la fonction partie entière, $(u_{n})$ la suite définie par :
$$u_{n}=n-pE\left(\dfrac{n}{p}\right).$$
Démontrer que $(u_{n})$ est périodique.
3) Soit $u_{n}$ le chiffre des unités de $n^{2}.$
Démontrer que $(u_{n})$ est périodique.
Préciser la période.
VIII. Représentation graphique d'une suite
Définition
On se place dans un repère $(O\;,\ \vec{i}\;,\ \vec{j}).$
La représentation graphique d'une suite $(u_{n})$ est l'ensemble des points de coordonnées $(n\;;\ u_{n}).$
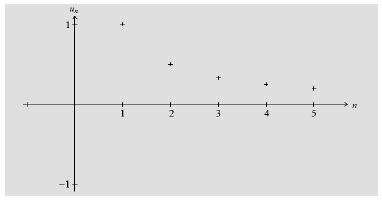
Exemple 1 : (Cas d'une suite définie explicitement)
Soit $(u_{n})$ la suite définie par $u_{n}=\dfrac{1}{n}$ pour $n\geq 1.$
Sa représentation graphique est l'ensemble des points isolés $(1\;;\ 1)$, $\left(2\;;\ \dfrac{1}{2}\right)$, $\left(3\;;\ \dfrac{1}{3}\right)$ ect ...
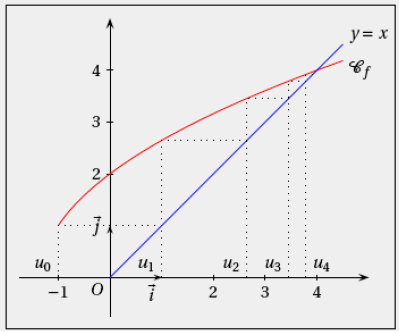
Exemple 2 : (Cas d'une suite récurrente de la forme $u_{n+1}=f(u_{n})$)
Dans ce cas, on ne cherche pas en général à représenter la suite définition ci-dessus mais on préfère représenter ses premiers termes sur l'axe des abscisses.
Pour ce faire, on suit les étapes suivantes
a) On trace la courbe représentative $\mathcal{C}_{f}$ de la fonction $f$ définissant la suite récurrente et de la première bissectrice d'équation $y=x$ ;
b) On place le premier terme $u_{0}$ sur l'axe des abscisses ;
c) On utilise $\mathcal{C}_{f}$ pour construire $u_{1}=f(u_{0})$ sur l'axe des ordonnées ;
d) On reporte $u_{1}$ sur l'axe des abscisses à l'aide de la première bissectrice ;
e) On utilise $\mathcal{C}_{f}$ pour construire $u_{2}=f(u_{1})$ sur l'axe des ordonnées ;
f) etc...
Voici un exemple de construction avec la suite $(u_{n})$ définie par $u_{0}=-1$ et, pour tout $n$ de $\mathbb{N}$, $u_{n+1}=\sqrt{3u_{n}+4}.$
N.B.
Ce type de construction permet de faire des conjectures en termes de variation, de comportement à l'infini, etc.
IX. Limite d'une suite
La notion de limite en $+\infty$ déjà rencontrée à propos des fonctions, s'étend au cas des suites.
Mais cette notion n'est définie que lorsque $n$ tend vers $+\infty.$
Dire qu'une suite $(u_{n})$ a pour limite le réel $\ell$ quand $n$ tend vers $+\infty$ signifie que tout intervalle ouvert de centre $\ell$. contient tous les termes de la suite, sauf un nombre fini d'entre eux.
Dire qu'une suite $(u_{n})$ a pour limite $+\infty$ quand $n$ tend vers $+\infty$ signifie que quel que soit le réel $A$, tous les termes de la suite sont supérieurs à $A$ à partir d'un certain rang.
On a les résultats suivants :
Théorème 1 :
a) $\lim_{n\rightarrow +\infty}\sqrt{n}=+\infty$ ;
$\lim_{n\rightarrow +\infty}n^{2}=+\infty$ ;
$\lim_{n\rightarrow +\infty}n^{3}=+\infty.$
b) $\lim_{n\rightarrow +\infty}\dfrac{1}{\sqrt{n}}=0$ ;
$\lim_{n\rightarrow +\infty}\dfrac{1}{n}=0$ ;
$\lim_{n\rightarrow +\infty}\dfrac{1}{n^{2}}=0$ ;
$\lim_{n\rightarrow +\infty}\dfrac{1}{n^{3}}=0.$
Théorème 2 :
Les résultats concernant les opérations sur les limites de fonctions s'étendent aux limites de suites.
Exemple :
Soit la suite $(u_{n})$ définie par :
$u_{n}=\dfrac{3n^{3}-5n^{2}+1}{2n^{3}+1}.$
Alors $\lim_{n\rightarrow +\infty}u_{n}=\lim_{n\rightarrow +\infty}\dfrac{3n^{3}}{2n^{3}}=\dfrac{3}{2}.$
Soit $(u_{n})$ une suite du type $u_{n}=f(n)$ :
Si $\lim_{x\rightarrow +\infty}f(x)=1$, alors $\lim_{n\rightarrow +\infty}u_{n}=1.$
(Nous admettrons ce résultat).
Les théorèmes vus sur les limites finies de fonctions s'appliquent donc aux suites de ce type.
En conséquence, on récupère dans ce cas tous les théorèmes sur les opérations algébriques, les limites de référence, ainsi que les théorèmes de comparaison, en particulier le théorème des ''gendarmes''.
Exemples :
1) Soit $\left(u_{n}\right)$ la suite définie sur $\mathbb{N}^{\ast}$ par $u_{n}=\dfrac{2n+3}{n+1}.$
On a $u_{n}=f(n)$ où $f$ est la fonction définie par $f(x)=\dfrac{2x+3}{x+1}.$
On sait que : $\lim_{x\rightarrow +\infty}\dfrac{2x+3}{x+1}=\lim_{x\rightarrow +\infty}\dfrac{2x}{x}=2.$
D'où : $\lim_{n\rightarrow +\infty}u_{n}=2.$
2) Soit $\left(u_{n}\right)$ la suite définie sur $\mathbb{N}^{\ast}$ par $u_{n}=\dfrac{\sin n}{n}.$
On a $u_{n}=f(n)$ où $f$ est la fonction définie par $f(x)=\dfrac{\sin x}{x}.$
On sait que pour tout $x$ strictement positif,
$$|\sin x|\leq 1\text{ puis : }0\leq\left|\dfrac{\sin x}{x}\right|\leq\dfrac{1}{x}.$$
Il résulte du théorème des gendarmes vu sur les fonctions et qui sera rappelé plus bas, que $\lim_{x\rightarrow +\infty}\dfrac{\sin x}{x}=0$ et par conséquent :
$\lim_{n\rightarrow +\infty}\dfrac{\sin n}{n}=0.$
3) Toute suite constante converge vers son premier terme.
X. Propriétés des suites convergentes
Nous admettrons toutes les propriétés suivantes :
P.1 : Toute suite convergente est bornée.
Attention ! Une suite peut être bornée et divergente (Ex : la suite $\left(u_{n}\right)$ de terme général $u_{n}=(-1)^{n}$).
On déduit de cette propriété que toute suite non bornée est divergente.
P.2 : Si la suite $\left(u_{n}\right)$ converge vers $l$, alors la suite $\left(|u_{n}|\right)$ converge vers $|l|.$
Attention ! Il se peut que la suite $\left(|u_{n}|\right)$ soit convergente et que la suite $\left((u_{n}\right)$ soit divergente (Reprendre l'exemple précédent : $u_{n}=(-1)^{n}).$
P.3 : Règles de comparaison
Soient $\left(u_{n}\right)$ et $\left(v_{n}\right)$ deux suites définies sur un même ensemble $E$ et $l$ un réel.
a) Si, à partir d'un certain rang, on a :
$\left|u_{n}-l\right|\leq v_{n}$ et si l'on a :
$\lim_{n\rightarrow +\infty}v_{n}=0,$ alors on a : $\lim_{n\rightarrow +\infty}u_{n}=l$
$\lim_{n\rightarrow +\infty}v_{n}=\lim_{n\rightarrow +\infty}w_{n}=l$, alors on a :
$\lim_{n\rightarrow +\infty}u_{n}=l.$
b) Si, à partir d'un certain rang, on a :
$v_{n}\leq u_{n}\leq w_{n}$ et si l'on a :
$\lim_{n\rightarrow +\infty}v_{n}=\lim_{n\rightarrow +\infty}w_{n}=l$, alors on a :
$\lim_{n\rightarrow +\infty}u_{n}=l.$
Ce dernier résultat est aussi connu sous le nom de théorème des gendarmes.
Exemple :
Soit $\left(u_{n}\right)$ la suite définie par :
$$u_{n}=\dfrac{1}{n^{2}+1}+\dfrac{1}{n^{2}+2}+\ldots+\dfrac{1}{n^{2}+n}.$$
Pour tout entier $p$ élément de ${1\;,\ 2,\ldots n}$, on a :
$n^{2}+1\leq n^{2}+p\leq n^{2}+n$, d'où :
$$\dfrac{1}{n^{2}+n}\leq\dfrac{1}{n^{2}+p}\leq\dfrac{1}{n^{2}+1}.$$
En sommant ces inégalités pour $p$ allant de $1$ à $n$, on obtient :
$$\dfrac{n}{n^{2}+n}\leq u_{n}\leq\dfrac{n}{n^{2}+1}.$$
Or, $\lim_{n\rightarrow +\infty}\dfrac{n}{n^{2}+n}=\lim_{n\rightarrow +\infty}\dfrac{n}{n^{2}+1}=\lim_{n\rightarrow +\infty}\dfrac{1}{n^{2}}=0$
(Application de la règle analogue sur la limite d'une fonction rationnelle à l'infini).
On en déduit, en utilisant le théorème des gendarmes, que $\lim_{n\rightarrow +\infty}u_{n}=0.$
P.4 : Limite et ordre
Si, à partir d'un certain rang, on a :
$u_{n}\leq v_{n}$ et si l'on a :
$\lim_{n\rightarrow +\infty}u_{n}=l$ et $\lim_{n\rightarrow +\infty}v_{n}=k$, alors on a : $l\leq k.$
Exercice
En déduire les deux propriétés suivantes :
P.5 : Si, à partir d'un certain rang, on a :
$u_{n}\geq 0$ et si l'on a :
$\lim_{n\rightarrow +\infty}u_{n}=l$, alors on a $l\geq 0.$
Autrement dit : la limite d'une suite convergente de réels positifs est un réel positif ou nul. $\dfrac{1}{n!}$
Attention : une suite à termes strictement positifs n'a pas nécessairement une limite strictement positive.
Exemple :
$u_{n}=\dfrac{1}{n}.\ \forall\,n\in\mathbb{N}^{\ast}\;,\ u_{n}>0$, mais $\lim_{n\rightarrow +\infty}u_{n}=0.$
P.6 : Si, à partir d'un certain rang, on a : $a\leq u_{n}\leq b$ et si $\left(u_{n}\right)$ est une suite convergente, alors sa limite appartient à l'intervalle $[a\;,\ b].$
XI. Suite arithmétique
Définition
$r$ étant une constante réelle, on appelle suite arithmétique toute suite récurrente $\left(u_{n}\right)$ définie par la donnée de son premier terme $U_{n_{0}}$ et par la relation de récurrence $u_{n+1}=u_{n}+r$ vérifiée pour tout $n\geq n_{0}.$
Tout terme d'une suite arithmétique est obtenu en ajoutant la raison $r$ de cette suite au terme précédent.
Si $\left(U\right)n\in\mathbb{N}$ est une suite arithmétique de raison , alors :
$U_{1}=U_{0}+r\;,\ U_{2}=U_{1}+r\;,\ldots\;,\ U_{n}=U_{n-1}+r\;,\ U_{n+1}=U_{n}+r\;,\ldots$
Relation entre trois termes consécutifs d'une suite arithmétique :
Si $a\;,\ b$ et $c$ sont dans cet ordre, les valeurs de trois termes consécutifs d'une suite arithmétique de raison , alors :
$r=b-a=c-b$ ; on a alors $2b=a+c$ ; ce qui donne $b=\dfrac{a+c}{2}$
On dit alors que tout terme d'une suite arithmétique, sauf le premier, est la démi-somme ou moyenne arithmétique des deux termes qui l'encadrent.
Par exemple, si $\left(U_{n}\right)n\in\mathbb{N}$ est une suite arithmétique alors
$$U_{1}=\dfrac{U_{0}+U_{2}}{2}\;,\ U_{10}=\dfrac{U_{9}+U_{11}}{2}\;,\ldots\;,\ U_{n}=\dfrac{U_{n-1}+U_{n+1}}{2}.$$
Relation entre deux termes quelconques $u_{n}$ et $u_{p}$ d'une suite arithmétique :
1) si $\left(u_{n}\right)$ est une suite arithmétique de raison $r$ alors :
$$\boxed{\forall\,n\in\mathbb{N}\;,\ u_{n}=u_{0}+nr}$$
Démonstration : par récurrence
$-\ \ $ initiation : $u_{0}=u_{0}+0r$
$-\ \ $ hérédité : supposons que pour $>0$ , $n$ fixé , $u_{n}=u_{0}+nr$
Comme $u_{n+1}=u_{n}+r$ alors d'après l'hypothèse de récurrence, $u_{n+1}=\left(u_{0}+nr\right)+r\;,\ u_{n+1}=u_{0}+(n+1)r$
Donc la propriété est héréditaire
Conclusion
$\forall\,n\in\mathbb{N}\;,\ u_{n}=u_{0}+nr.$
2) $u_{n}$ et $u_{p}$ étant deux termes quelconques d'une suite arithmétique de raison $r$, on a $\boxed{u_{n}=u_{p}+(n-p)r}$
Démonstration :
on sait que $u_{n}=u_{0}+nr$ et que $u_{p}=u_{0}+pr$
Donc $u_{n}-u_{p}=u_{0}+nr-u_{0}-pr$
D'où $u_{n}-u_{p}=(n-p)r$
on a alors $u_{n}=u_{p}(n-p)r$
Sens de variation d'une suite arithmétique
$\left(u_{n}\right)$ étant une suite arithmétique de raison $r$ on a :
$u_{n+1}-u_{n}=r$ pour tout indice $n$.
on en déduit qu'une suite arithmétique de raison $r$, est :
$-\ \ $ strictement croissante si et seulement si $r>0$
$-\ \ $ strictement décroissante si et seulement si $r>0$
$-\ \ $ constante si et seulement si $r=0$
Convergence d'une suite arithmétique de raison $r$
On a : $\forall\,n\in\mathbb{N}$, $u_{n}=u_{0}+nr$
Donc $\lim_{x\rightarrow +\infty}u_{n}=\lim_{x\rightarrow +\infty}\left(u_{0}+nr\right)=\lim_{x\rightarrow +\infty}nr\text{ si }r\neq 0$
Auteur:
Ka, Faye & Mbengue

Commentaires
Anonyme (non vérifié)
jeu, 08/13/2020 - 14:50
Permalien
Formidable
Bcp (non vérifié)
lun, 06/20/2022 - 20:35
Permalien
C’est très important mais
Ajouter un commentaire