Translation et vecteur - 4e
Classe:
Quatrième
I. La translation
I.1 Définition
Soit $A\ $ et $\ B$ deux points du plan. On appelle la translation de tout point $M$ du plan qui amène $A$ en $B$, le déplacement de celui-ci parallèlement à $[AB)$ et dans le sens de $[AB).$
La translation est souvent notée par la lettre $t.$
Donc, $t_{A\rightarrow B}$ est la translation qui amène $A$ en $B$ et $\ t_{B\rightarrow A}$ est la translation qui amène $B$ en $A.$
Si $M'$ est l'image de $M$ par $t_{A\rightarrow B}$ alors :
$\centerdot\ (MM')//(AB)$
$\centerdot\ MM'=AB$
$\centerdot\ [AB)\ $ et $\ [MM')$ ont même sens.
I.2. Construction et propriétés
a) Image d'un point
Soit $A\;,\ B\ $ et $\ M$ des points du plan. Construisons $M'$ image de $M$ par la translation qui amène $A$ en $B\ $ et $\ M''$ l'image de $M$ par la translation qui amène $B$ en $A.$
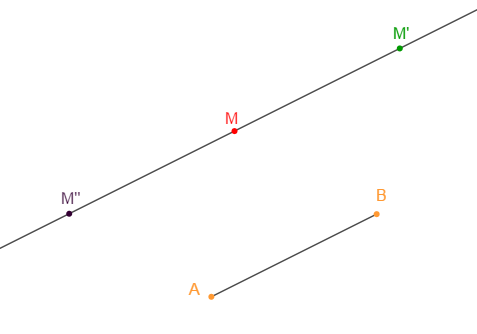
$$t_{A\rightarrow B}(M)=M'\left\lbrace\begin{array}{l} \centerdot\ (MM')//(AB)\\ \\\centerdot\ MM'=AB\\ \\\centerdot\ [MM')\ \text{ et }\ [AB)\ \text{ont même sens}\end{array}\right.$$
$$t_{B\rightarrow A}(M)=M''\left\lbrace\begin{array}{l} \centerdot\ (MM'')//(AB)\\ \\\centerdot\ MM''=AB\\ \\\centerdot\ [MM'')\ \text{ et }\ [BA)\ \text{ont même sens}\end{array}\right.$$
b) Image d'un segment
Soit $A\ $ et $\ B$ deux points du plan. $[IJ]$ un segment du plan.
Construisons l'image de $[IJ]$ par la translation qui amène $A$ en $B.$
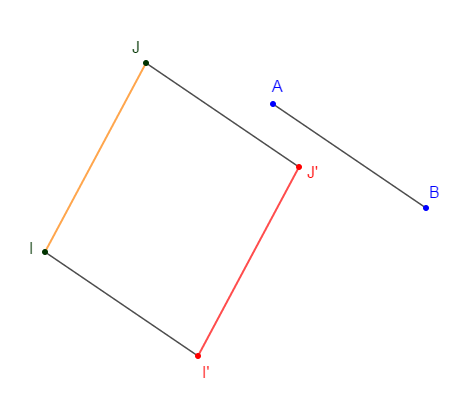
$IJ=I'J'$
$(IJ)//(I'J')$
Propriété
L'image d'un segment par une translation est un segment de même longueur qui lui est parallèle.
c) Image d'une droite
Soit $(\Delta)$ une droite, $A\ $ et $\ B$ deux points du plan. Construisons l'image de $(\Delta)$ par la translation qui amène $A$ en $B.$
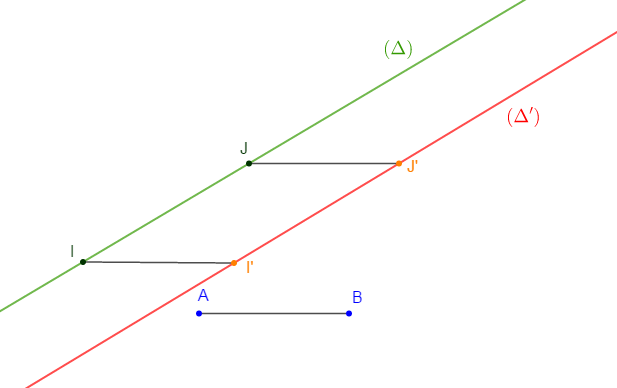
Propriété
L'image d'une droite par une translation est une droite qui lui est parallèle.
Application
Soit $\widehat{ABC}$ un angle de $45^{\circ}.$
$I\ $ et $\ J$ deux points du plan.
1) Construire l'image de $\widehat{ABC}$ par la translation qui transforme $J$ en $I.$
2) Que constates-tu ?
Solution
1) Construction
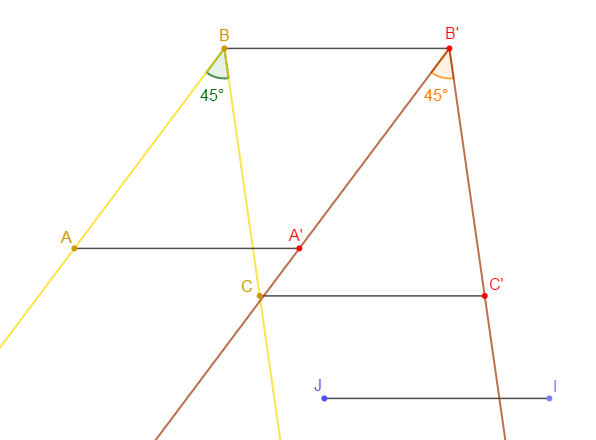
2) On constate que $mes\;\widehat{ABC}=mes\;\widehat{A'B'C'}$
Propriété
L'image d'un angle par une translation est un angle de même mesure.
II. Vecteur
II.1. Définition et notation
Soit $A\ $ et $\ B$ deux points du plan. Le vecteur $(A\;,\ B)$ est noté $\overrightarrow{AB}$ et il est déterminé par :
$-\ $ sa direction : celle de la droite $(AB)$
$-\ $ son sens : le sens de $A$ vers $B$ ou bien le sens du couple $(A\;,\ B)$
$-\ $ sa longueur : la longueur du segment $[AB]$
Exemple
Marquer les points $A\ $ et $\ A'$ tels que $A$ soit distant de $A'$ de $4\;cm.$
Donner les sens, directions et longueurs des vecteurs $\overrightarrow{AA'}\ $ et $\ \overrightarrow{A'A}$
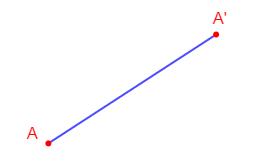
$$\overrightarrow{AA'}\left\lbrace\begin{array}{l} -\ \text{direction : celle de la droite } (AA')\\ \\-\ \text{sens : de } A\ \text{ vers } A'\\ \\-\ \text{longueur : celle du segment } [AA'] \text{ égale à } 4\;cm\end{array}\right.$$
$$\overrightarrow{A'A}\left\lbrace\begin{array}{l} -\ \text{direction : celle de la droite } (A'A)\\ \\-\ \text{sens : de } A'\ \text{ vers } A\\ \\-\ \text{longueur : celle du segment } [A'A] \text{ égale à } 4\;cm\end{array}\right.$$
N.B : Si $\vec{u}$ est un vecteur du plan tel que $\vec{u}=\overrightarrow{AB}$ où $A\ $ et $\ B$ sont des points du plan alors, on dit que le vecteur $\vec{u}$ est un représentant du vecteur $\overrightarrow{AB}.$
II.2. Vecteurs égaux
Deux vecteurs sont dits égaux s'ils ont même direction, même sens et même longueur.
N.B : Si $\vec{u}$ est un vecteur du plan alors, son opposé est noté $-\vec{u}.$ Il a la même direction, la même longueur que le vecteur $\vec{u}$ mais de sens opposé à celui de $\vec{u}.$
Exemple
Soit $ABCD$ est un parallélogramme
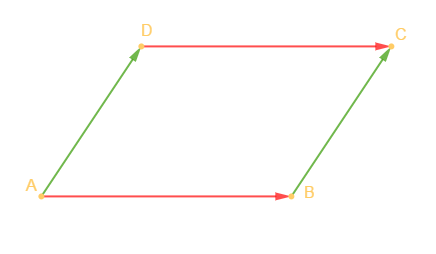
alors, on a :
$\overrightarrow{AB}=\overrightarrow{DC}\ $ et $\ \overrightarrow{BA}=\overrightarrow{CD}$
$\overrightarrow{BA}\ $ et $\ \overrightarrow{DC}$ sont opposés $\overrightarrow{BA}=-\overrightarrow{DC}$
II.3. Parallélogramme et vecteur
$-\ $ Si $ABCD$ est un parallélogramme alors $\overrightarrow{AB}=\overrightarrow{DC}$
$-\ $ Si $\overrightarrow{AB}=\overrightarrow{DC}$ alors, $ABCD$ est un parallélogramme (voir l'exemple précédent)
II.4. Milieu d'un segment et vecteur
$-\ $ Si un point $I$ est milieu d'un segment $[AB]$ alors,
$$\overrightarrow{AI}=\overrightarrow{IB}$$
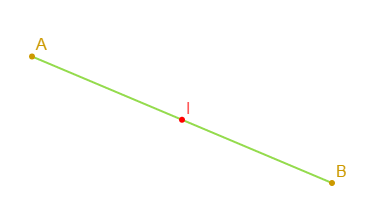
$-\ $ Si les points $A\;,\ B\ $ et $\ I$ sont tels que $\overrightarrow{AI}=\overrightarrow{IB}$ alors, $I$ est milieu du segment $[AB].$
En effet, $\overrightarrow{AI}+\overrightarrow{BI}=\vec{0}$ (vecteur nul)
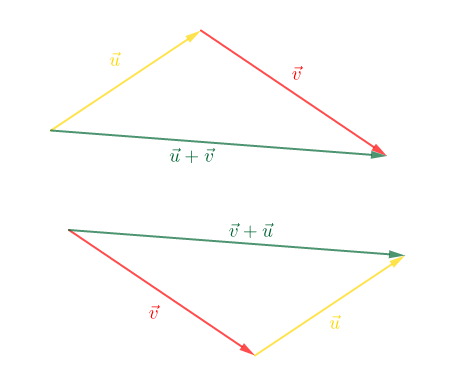
II.5. Somme des vecteurs
Soit $\vec{u}\ $ et $\ \vec{v}$ deux vecteurs du plan.
$\vec{u}+\vec{v}$ est aussi un vecteur du plan.
Application
Construire $ABCD$ un parallélogramme. Indiquer sur la même figure les vecteurs suivants :
$$\overrightarrow{AB}+\overrightarrow{AC}\;,\quad\overrightarrow{AD}+\overrightarrow{DC}$$
Solution
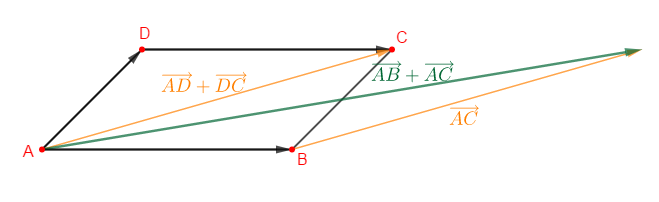
N.B : Pour tout vecteur $\overrightarrow{AB}$ du plan et $M$ un point du plan, on a :
$$\overrightarrow{AB}=\overrightarrow{AM}+\overrightarrow{MB}$$
C'est la relation de Chasles.
Auteur:
Mamadou Siradji Dia

Commentaires
Anonyme (non vérifié)
ven, 06/10/2022 - 15:58
Permalien
Je suis Professeur. Et j
Ajouter un commentaire