Équation et Inéquation à une seule inconnue 3e
Classe:
Troisième
I. Équation
I.1 Équation produit ou équation de la forme (ax+b)(cx+d)=0
La résolution de ce type d'équation s'appuie sur la propriété suivante : un produit de facteurs est nul si l'un de ses facteurs est nul.
On a : XY=0 si, et seulement si, X=0 ou Y=0
Exemple 1 :
Résolvons les équations suivantes
⋅ (4x−5)(−3x+7)=0
On aura : 4x−5=0 ou −3x+7=0
Alors, 4x=5 ou −3x=−7
Donc, x=54 ou x=−7−3=73
D'où S={54; 73}
⋅ (23x−4)(32x+54)=0
On aura : 23x−5=0 ou 32x+54=0
Alors, 23x=4 ou 32x=−54
Donc, x=4×32=6 ou x=−5−4×23=−56
D'où S={−56; 6}
Exemple 2 :
Certaines équations n'étant pas présentées initialement sous la forme d'équation produit peuvent l'être par la suite par une simple utilisation des techniques de la factorisation.
Résolvons les équations suivantes :
⋅ 4x2=9
On aura : (2x−3)(2x+3)=0
Alors, 2x−3=0 ou 2x+3=0
Donc, 2x=3 ou 2x=−3
Par suite, x=32 ou x=−32
D'où S={−32; 32}
⋅ (3x−2)2=(−2x+3)2
On aura : (3x−2)2−(−2x+3)2=0
Alors, [(3x−2)−(−2x+3)][(3x−2)+(−2x+3)]=0
Donc, (5x−5)(x+1)=0
Par suite, 5x−5=0 ou x+1=0
Ainsi, x=55=1 ou x=−1
D'où S={−1; 1}
⋅ (3x−2)2+(3x−2)(x+3)+(3x−2)=0
On aura : (3x−2)[(3x−2)+(x+3)+1]=0
Alors, (3x−2)(4x+2)=0
Donc, 3x−2=0 ou 4x+2=0
Ainsi, x=23 ou x=−24=−12
D'où S={−12; 23}
I.2 Équation du type |ax+b|=c avec c≥0
La résolution de ce type d'équation s'appuie sur la propriété suivante :
|X|=Y avec Y≥0 si, et seulement si, X=Y ou X=−Y
Exemple 1 : résolvons les équations suivantes
⋅ |3x−5|=7
On aura : 3x−5=7 ou 3x−5=−7
Alors, 3x=12 ou 3x=−2
Donc, x=123=4 ou x=−23
D'où S={−23; 4}
⋅ |−23x+5|=3
On aura : −23x+5=3 ou −23x+5=−3
Alors, −23x=−2 ou −23x=−8
Donc, x=(−2)(−32)=3 ou x=(−8)(−32)=12
D'où S={3; 12}
Exemple 2 : certaines équations n'étant pas présentées sous la forme |ax+b|=c peuvent l'être par la suite, par une utilisation double des deux propriétés suivantes :
si {a≥0b≥0a=balors √a=√b et √X2=|X|
Résolvons les équations suivantes :
⋅ 4x2−9=0
On aura : 4x2=9
Alors, x2=94
Donc, √x2=√94
Par suite |x|=32
Ainsi, x=32 ou x=−32
D'où S={−32; 32}
⋅ 3(2x+6)2=108
On aura : (2x+6)2=1083
Alors, √(2x+6)2=√36
Donc, |2x+6|=6
Par suite 2x+6=6 ou 2x+6=−6
Ainsi, x=0 ou x=−6
D'où S={−6; 0}
Remarques :
Si c<0 l'équation |ax+b|=c n'admet pas de solutions (car une valeur absolue n'est jamais négative).
On écrira S=∅
I.3 Équation du type |ax+b|=|cx+d|
La résolution de ce type d'équation s'appuie sur la propriété suivante :
|X|=|Y| si, et seulement si, X=Y ou X=−Y
Exemple 1 : résolvons les équations suivantes
⋅ |2x−3|=|−3x+7|
On aura : 2x−3=−3x+7 ou 2x−3=3x−7
Alors, 5x=10 ou −x=−4
Donc, x=2 ou x=4
D'où S={2; 4}
⋅ 2|32x+5|=3|23x−4|
On aura : 2(32x+5)=3(23x−4) ou 2(32x+5)=−3(23x−4)
Alors, 3x+10=2x−12 ou 3x+10=−2x+12
Donc, x=−22 ou 5x=2
Ainsi, x=−22 ou x=25
D'où S={−22; 25}
Exemple 2 : certaines équations n'étant pas présentées sous la forme |ax+b|=|cx+d| peuvent l'être par la suite, par une simple utilisation des deux propriétés suivantes
si {a≥0b≥0a=balors √a=√b et √X2=|X|
Résolvons les équations suivantes :
⋅ (3x−5)2=(−2x+7)2
On aura : √(3x−5)2=√(−2x+7)2
Alors, |3x−5|=|−2x+7|
Donc 3x−5=−2x+7 ou 3x−5=2x−7
Par suite 5x=12 ou x=−2
Ainsi, x=125 ou x=−2
D'où S={−2; 125}
⋅ 4(3x−2)2=9(2x+3)2
On aura : √4(3x−2)2=√9(2x+3)2
Alors, 2|3x−2|=3|2x+3|
Donc 2(3x−2)=3(2x+3) ou 2(3x−2)=3(−2x−3)
Par suite 6x−4=6x+9 ou 6x−4=−6x−9
Ainsi, 0=13 (impossible) ou 12x=−5
Ce qui donne x=−512
D'où S={−512}
I.4 Équation faisant intervenir des quotients
La résolution de ce type d'équation s'appuie tout d'abord sur une étude de la condition d'existence de l'équation et dans le cas où la condition d'existence est posée on procède tout simplement à une réduction au même dénominateur et par suite à une élimination des dénominateurs.
Sera solution toute valeur trouvée et différente des valeurs posées au niveau de la condition d'existence.
Exemple : résolvons les équations suivantes
⋅ 2x−33x−2=0
L'équation existe si, et seulement si, 3x−2≠0 c'est à dire x≠23.
Pour x≠23, l'équation devient 2x−3=0 c'est à dire x=32
D'où S={32}
⋅ 3x−22x−3=12
l'équation existe si, et seulement si, 2x−3≠0 c'est à dire x≠32.
Pour x≠32, l'équation devient
6x−4=2x−34x=1x=14
D'où S={14}
⋅ 33x−2+22x−3=0
L'équation existe si, et seulement si, 3x−2≠0 et 2x−3≠0 c'est à dire x≠23 et x≠32
Pour x≠23 et x≠32, l'équation devient
3(2x−3)+2(3x−2)=06x−9+6x−4=012x=13x=1312
D'où S={1312}
II Inéquation
II.1 Inéquation produit ou inéquation de la forme (ax+b)(cx+d)≤0
Exemple 1 : résolvons les inéquations suivantes
⋅ (2x+6)(−3x+3)≤0
On a : (2x+6)(−3x+3)=0 si, et seulement si, 2x+6=0 ou −3x+3=0
c'est à dire x=−3 ou x=1
x−∞−31+∞2x+6−0+|+−3x+3+|+0−(2x+6)(−3x+3)−0+0−
S=]−∞; −3]∪[1; +∞[
⋅ −2x(3x+2)(x+)2≥0
On a : −2x(3x+2)(x+)2=0 si, et seulement si, −2x=0 ou 3x+2=0 ou (x+1)2=0
Alors, x=0 ou x=−23 ou x=−1
x−∞−1−2/30+∞−2x+|+|+0−3x+2−|−0+|+(x+1)2+0+|+|+−2x(3x+2)(x+)2−0−0+0−
S=[−23; 0]
⋅ (3−x)(4+x)<0
On a : (3−x)(4+x)=0 si, et seulement si, 3−x=0 ou 4+x=0
Alors, x=3 ou x=−4
x−∞−43+∞3−x+|+0−4+x−0+|+(3−x)(4+x)−0+0−
S=]−∞; −4[∪]3; +∞[
Exemple 2 : résolvons les inéquations suivantes
⋅ 4x2−9<0
On aura : (2x−3)(2x+3)<0
Alors, (2x−3)(2x+3)=0 si, et seulement si, 2x−3=0 ou 2x+3=0
Donc x=32 ou x=−32
x−∞−3/23/2+∞2x−3−|−0+2x+3−0+|+(2x−3)(2x+3)+0−0+
S=]−32; 32[
⋅ (2x−7)2−(2x−3)2≥0
On aura : [(2x−7)−(2x−3)][(2x−7)+(2x−3)]≥0
Alors, (−4)(4x−10)=0 si, et seulement si, 4x−10=0 c'est à dire x=52
x−∞5/2+∞−4−|−4x−10−0+−4(4x−10)+0−
S=]−∞; 52]
II.2 Inéquation du type |ax+b|≤c avec c>0
La résolution de ce type d'inéquation s'appuie sur la propriété suivante :
|X|≤Y avec Y≥0 si, et seulement si, X≤Y et X≥−Y
Exemple 1 : résolvons les inéquations suivantes
⋅ |−2x+3|≤5
On aura : −2x+3≤5 et −2x+3≥−5
Alors, −2x≤2 et −2x≥−8
Donc, x≥−1 et x≤4

D'où S=[−1; 4]
⋅ |23x−4|≤2
On aura : 23x−4≤2 et 23x−4≥−2
Alors, 23x≤6 et 23x≥2
Donc, x≤6×32 et x≥2×32
Ainsi, x≤9 et x≥3
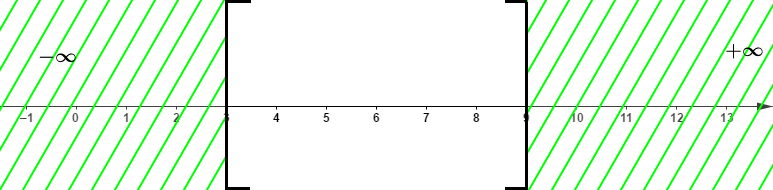
D'où S=[3; 9]
Exemple 2 : certaines inéquations n'étant pas présentées sous la forme |ax+b|≤c peuvent l'être par la suite, par une utilisation successive des deux propriétés suivantes
si {a≥0b≥0a≤balors √a≤√b et √X2=|X|
Résolvons les inéquations suivantes :
⋅ 4x2−9<0
On aura : 4x2<9
Alors, x2<94
Donc, √x2<√94
Par suite |x|<32
Ainsi, x<32 et x>−32
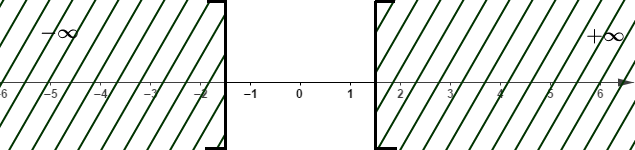
D'où S=]−32; 32[
⋅ −2(x+3)2≥−32
On aura : (x+3)2≤−32−2
Alors, √(x+3)2≤√16
Donc, |x+3|≤4
Par suite x+3≤4 et x+3≥−4
Ainsi, x≤1 et x≥−7
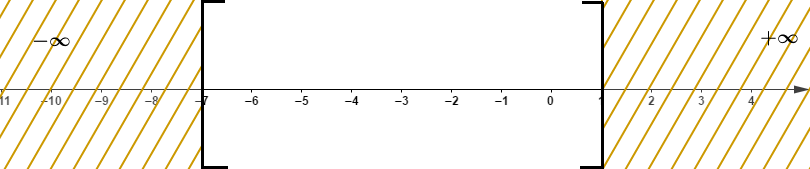
D'où S=[−7; 1]
Remarques :
Si c<0 l'inéquation |ax+b|≤c n'admettra pas de solutions.
On écrira S=∅
II.3 Inéquation du type |ax+b|≥c avec c≥0
La résolution de ce type d'inéquation s'appuie sur la propriété suivante :
|X|≥Y avec Y≥0 si, et seulement si, X≥Y ou X≤−Y
Exemple 1 : résolvons les inéquations suivantes
⋅ |−2x+7|≥5
On aura : −2x+7≥5 ou −2x+7≤−5
Alors, −2x≥−2 ou −2x≤−12
Donc, x≤1 ou x≥6
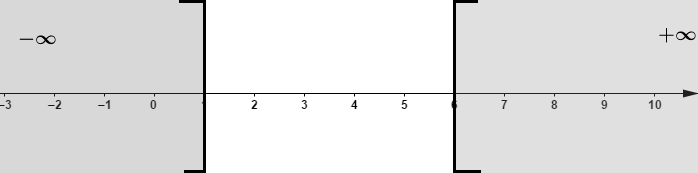
D'où S=]−∞; 1]∪[6; +∞[
⋅ |23x−3|>5
On aura : 23x−3>5 ou 23x−3<−5
Alors, 23x>2 ou 23x<−2
Donc, x>8×32 ou x<−2×32
Ainsi, x>12 ou x<−3
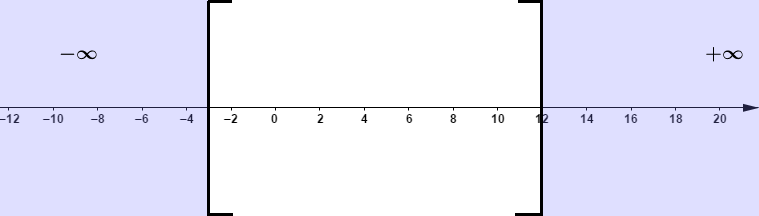
S=]−∞; −3[∪]12; +∞[
Exemple 2 : certaines inéquations n'étant pas présentées sous la forme |ax+b|≥c peuvent l'être par la suite, par une utilisation successive des deux propriétés suivantes
si {a≥0b≥0a≥balors √a≥√b et √X2=|X|
Résolvons les inéquations suivantes :
⋅ 25x2−49≥0
On aura : 25x2≥49
Alors, x2≥4925
Donc, √x2≥√4925
Par suite |x|≥75
Ainsi, x≥75 ou x≤−75
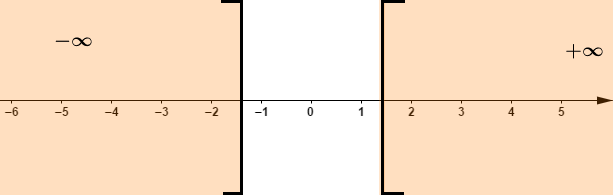
D'où S=]−∞; −75]∪[75; +∞[
⋅ −2(x+3)2<−50
On aura : (x+3)2>−50−2
Alors, √(x+3)2>√25
Donc, |x+3|>5
Par suite x+3>5 ou x+3<−5
Ainsi, x>2 ou x<−8
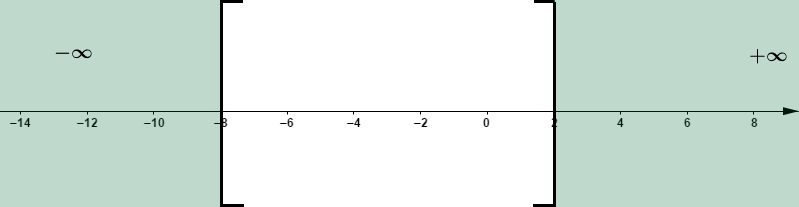
D'où S=]−∞; −8[∪]2; +∞[
Remarques :
Si c<0 l'inéquation |ax+b|>c est toujours vraie, c'est à dire toute valeur de x est solution.
On écrira S=R ou S=]−∞; +∞[
II.4 Inéquation faisant intervenir les quotients
Exemples : résolvons les inéquations suivantes :
⋅ 2x−3−3x+2≥0
L'inéquation existe si, et seulement si, −3x+2≠0, c'est à dire x≠23.
L'inéquation est nulle si, et seulement si, 2x−3=0, c'est à dire x=32.
x−∞2/33/2+∞2x−3−|−0+−3x+2+0−|−2x−3−3x+2−||+0−
S=]23; 32]
⋅ −3(x+1)22x(−x+3)≤0
L'inéquation existe si, et seulement si, 2x(−x+3)≠0, c'est à dire 2x≠0 et −x+3≠0
Ce qui donne x≠0 et x≠3
L'inéquation est nulle si, et seulement si, −3(x+1)2=0, c'est à dire x+1=0.
Ce qui donne x=−1
x−∞−103+∞−3−|−|−|−(x+1)2+0+|+|+2x−|−0+|+−x+3+|+|+0−−3(x+1)22x(−x+3)+0+||−||+
S=]0; 3[∪{−1}
Auteur:
Abdoulaye Ba
Lien cours vidéo:

Commentaires
KHALIFA ABABACA... (non vérifié)
sam, 06/23/2018 - 02:02
Permalien
commentaire
Anonyme (non vérifié)
dim, 01/27/2019 - 16:41
Permalien
Telecharger les pages
Alassane Dia (non vérifié)
mar, 04/19/2022 - 11:45
Permalien
Excellent travail
Anonyme (non vérifié)
mer, 01/18/2023 - 18:15
Permalien
Comment télécharger vos
Philo (non vérifié)
jeu, 02/01/2024 - 21:41
Permalien
Excellent comme d'habitude
Ajouter un commentaire