Vous êtes ici

Corrigé BFEM Maths 2017

Exercice 1

On donne trois réels

$a\;,\ b\$ et

$\ c$ tels que :

$a=7-5\sqrt{2}\;;\quad b=-7-5\sqrt{2}\quad\text{et}\quad c=-7+5\sqrt{2}$

1) Démontrons que le réel

$a$ est l'inverse du réel

$b.$

On a :

$a\$ et

$\ b$ sont inverses si, et seulement si,

$a\times b=1$

Donc, calculons le produit

$a.b$

On a :

$\begin{array}{rcl} a\times b&=&(7-5\sqrt{2})(-7-5\sqrt{2})\\\\&=&(-5\sqrt{2}+7)(-5\sqrt{2}-7)\\\\&=&(-5\sqrt{2})^{2}-(7)^{2}\\\\&=&25\times 2-49\\\\&=&50-49\\\\&=&1\end{array}$

Ainsi,

$a.b=1$ , d'où

$a$ est l'inverse de

$b.$

2) Justifions que

$a\$ et

$\ c$ sont opposés.

On a :

$c=-7+5\sqrt{2}=-(7-5\sqrt{2})$

donc, on voit bien que

$c=-a$

Ce qui prouve que

$a\$ et

$\ c$ sont opposés.

3) Démontrons que

$\dfrac{b}{a}-\dfrac{c}{b}=b^{2}+c^{2}$

En réduisant au même dénominateur on obtient :

$\dfrac{b}{a}-\dfrac{c}{b}=\dfrac{b^{2}-ac}{ab}$

or,

$\ ab=1$ puisque

$a\$ et

$\ c$ sont inverses

donc,

$\dfrac{b^{2}-ac}{ab}=b^{2}-ac$

mais comme

$a\$ et

$\ c$ sont opposés alors,

$a=-c$

par suite,

$b^{2}-ac=b^{2}-(-c)c=b^{2}+c^{2}$

Ce qui montre que

$\dfrac{b}{a}-\dfrac{c}{b}=b^{2}+c^{2}$

4) Calculons

$a^{2}$

On a :

$\begin{array}{rcl} a^{2}&=&(7-5\sqrt{2})^{2}\\ \\&=&7^{2}-2\times 7\times 5\sqrt{2}+(-5\sqrt{2})^{2}\\ \\&=&49-70\sqrt{2}+25\times 2\\ \\&=&49+50-70\sqrt{2}\\ \\&=&99-70\sqrt{2}\end{array}$

dons,

$\boxed{a^{2}=99-70\sqrt{2}}$

Déduisons-en une écriture simplifiée du réel

$w=\sqrt{99-70\sqrt{2}}$

On a :

$w=\sqrt{99-70\sqrt{2}}$

or,

$99-70\sqrt{2}=a^{2}$

donc,

$w=\sqrt{a^{2}}=|a|$

Cherchons alors le signe de

$a$

On a :

$7^{2}=49\$ et

$\ (5\sqrt{2})=5^{2}\times 2=50$

Comme

$49$ est inférieur à

$50$ et que 7 et

$5\sqrt{2}$ sont tous des réels positifs alors,

$7$ est inférieur à

$5\sqrt{2}$

par suite,

$7-5\sqrt{2}<0$ ; donc,

$|a|=-a$

par conséquent,

$w=|a|=-7+5\sqrt{2}$

d'où,

$\boxed{w=-7+5\sqrt{2}}$

Exercice 2

Les notes des 160 candidats à un concours sont consignées dans le tableau suivant :

$\begin{array}{|c|c|c|c|c|c|}\hline\text{Notes}&[10\;;\ 12[&[12\;;\ 14[&[14\;;\ 16[&[16\;;\ 18[&[18\;;\ 20[\\ \hline\text{Fréquences}&0.3&x&0.2&0.15&y \\ \hline\end{array}$

1) La valeur

$0.3$ , fréquence de la classe

$[10\;;\ 12[$ permet de dire que

$30\%$ des candidats ont une note comprise entre 10 et 12.

C'est aussi pareil de dire que $70\%$ des élèves ont une note supérieure ou égale à 12.

2) Calcule

$x\$ et

$\ y$ sachant que

$25\%$ des élèves ont une note supérieure ou égale à 16.

On sait que la fréquence des élèves ayant une note supérieure ou égale à 16 est donnée par le cumul des fréquences des classes

$[16\;;\ 18[\$ et

$\ [18\;;\ 20[.$

Cette même fréquence est aussi égale à

$25\%=0.25$

Donc,

$0.15+y=0.25$

Ce qui donne :

$y=0.25-0.15=0.1$

D'où,

$\boxed{y=0.1}$

Pour calculer

$x$ on utilise le fait que la somme des fréquences est égale à 1.

On a alors :

$0.3+x+0.2+0.15+y=1\$ or,

$y=0.1$

donc,

$0.3+x+0.2+0.15+0.1=1$

par suite,

$x+0.75=1$

par conséquent,

$x=1-0.75=0.25$

Ainsi,

$\boxed{x=0.25}$

3) On donne

$x=0.25\$ et

$\ y=0.1$

a) Calculons la moyenne des notes.

Pour cela calculons d'abord le centre de chaque classe.

On a :

$\begin{array}{|c|c|c|c|c|c|}\hline\text{Notes}&[10\;;\ 12[&[12\;;\ 14[&[14\;;\ 16[&[16\;;\ 18[&[18\;;\ 20[\\ \hline\text{Fréquences}&0.3&0.25&0.2&0.15&0.1 \\ \hline\text{Centres}&11&13&15&17&19 \\ \hline \end{array}$

Ensuite, multiplions chaque centre par la fréquence correspondante.

Enfin, la moyenne des notes sera obtenue en additionnant les produits des centres et fréquences.

Ainsi,

$\begin{array}{rcl} M&=&(0.3\times 11)+(0.25\times 13)+(0.2\times 15)+(0.15\times 17)+(0.1\times 19)\\\\&=&3.3+3.25+3+2.55+1.9\\ \\&=&14\end{array}$

D'où,

$\boxed{M=14}$

b) Construisons le diagramme des fréquences cumulées décroissantes.

Le calcul des fréquences cumulées décroissantes est présenté dans le tableau suivant :

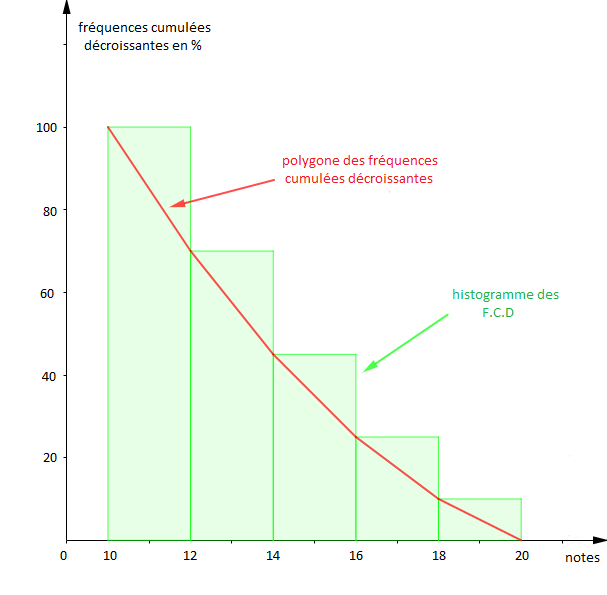
$\text{Diagramme des fréquences cumulées décroissantes}$

Exercice 3

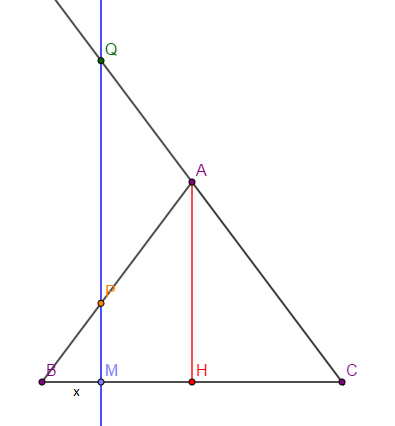
Soit

$ABC$ un triangle isocèle en

$A.$

La hauteur issue de

$A$ coupe le segment

$[BC]$ en

$H.$ On donne

$BC=6\;cm\quad\text{et}\quad AH=4\;cm$

Soit

$M$ le point du segment

$[BH]$ tel que

$BM=x.$

La parallèle à la droite

$(AH)$ et passant par

$M$ coupe la droite

$(AB)$ en

$P$ et la droite

$(AC)$ en

$Q.$

1) Faisons la figure

Calculons

$BH$

$ABC$ étant un triangle isocèle en

$A$ alors, la hauteur issue de

$A$ est aussi la médiatrice du segment

$[BC].$

Donc,

$H$ est milieu de

$[BC]$

ainsi,

$BH=\dfrac{BC}{2}=\dfrac{6}{2}=3$

D'où,

$\boxed{BH=3\;cm}$

2) Montre que

$\dfrac{MP}{AH}=\dfrac{x}{3}.$

On a : les droites sécantes

$(AB)$ et

$(BC)$ coupées par les parallèles

$(MP)$ et

$(AH)$ alors,

$ABH$ et

$BPM$ sont deux triangles en position de Thalès.

Donc, d'après le théorème de Thalès on aura :

$\dfrac{MP}{AH}=\dfrac{BM}{BH}$

or,

$BM=x\$ et

$\ BH=3$

Ce qui donne alors,

$\boxed{\dfrac{MP}{AH}=\dfrac{x}{3}}$

En déduisons

$MP$ en fonction de

$x.$

On a :

$\dfrac{MP}{AH}=\dfrac{x}{3}$

alors,

$MP=AH\times\dfrac{x}{3}$ ; or

$AH=4$

donc,

$MP=4\times\dfrac{x}{3}=\dfrac{4}{3}x$

d'où,

$\boxed{MP=\dfrac{4}{3}x}$

3) Exprimons

$MC$ en fonction de

$x.$

On a :

$BM+MC=BC$

alors,

$MC=BC-BM$ ; or

$BM=x\$ et

$\ BC=6$

donc,

$MC=6-x$

d'où,

$\boxed{MC=(6-x)}$

4) Montrons que

$MQ=\dfrac{4}{3}(6-x).$

On a : les droites sécantes

$(AC)$ et

$(BC)$ coupées par les parallèles

$(MQ)$ et

$(AH)$ alors,

$AHC$ et

$QMC$ sont deux triangles en situation de Thalès.

Donc, d'après le théorème de Thalès on aura :

$\dfrac{AH}{MQ}=\dfrac{HC}{MC}$

Ainsi,

$MQ\times HC=AH\times MC$

par suite,

$MQ=\dfrac{AH\times MC}{HC}$

or,

$AH=4\;,\ MC=6-x\$ et

$\ HC=3$

par conséquent,

$\boxed{MQ=\dfrac{4}{3}(6-x)}$

5) Cherchons les valeurs de

$x$ vérifiant

$MQ=3MP$

On a :

$MQ=3MP$ si, et seulement si,

$\dfrac{4}{3}(6-x)=3\times\dfrac{4}{3}x$

Donc, en résolvant cette équation on trouvera les valeurs de

$x$ vérifiant la relation

$MQ=3MP.$

On a :

$\dfrac{4}{3}(6-x)=3\times\dfrac{4}{3}x$ si, et seulement si,

$(6-x)=3x$

on aura alors :

$4x=6$

donc,

$x=\dfrac{6}{4}=\dfrac{3}{2}$

d'où,

$\boxed{x=\dfrac{3}{2}}$

6) Donnons alors la position du point

$P$ sur le segment

$[AB].$

La valeur

$x=\dfrac{3}{2}$ signifie que le point

$M$ est milieu de

$BH.$

Or, dans le triangle

$ABH$ la droite

$(MP)$ est parallèle à

$(AH)$ et passe par le point

$M$ milieu de

$[BH].$

Donc, d'après la réciproque de la propriété de la droite des milieux dans un triangle,

$(MP)$ passe aussi par le milieu de

$[AB].$

D'où,

$P$ est milieu de

$[AB].$

Exercice 4

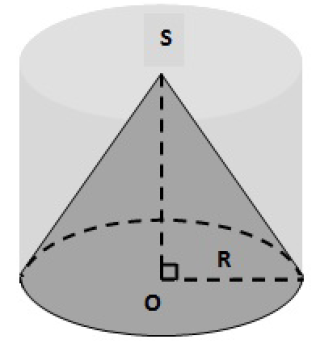
On considère la figure codée ci-dessous.

On donne les formules de calcul de volume de solides ci-dessous :

Volume d'un cône de révolution :

$V_{\text{cône}}=\dfrac{1}{3}\times\pi\times R^{2}\times h$

Volume d'une boule :

$V_{\text{boule}}=\dfrac{4}{3}\times\pi\times R^{3}$

Volume d'un cylindre :

$V_{\text{cylindre}}=\pi\times R^{2}\times h$

$R$ désigne le rayon et

$h$ la hauteur

1) Calculons le volume exact de chacun de ces trois solides pour

$h=R=1\;m$

$-\$ volume d'un cône de révolution :

On a :

$\begin{array}{rcl} V_{\text{cône}}&=&\dfrac{1}{3}\times\pi\times R^{2}\times h\\ \\&=&\dfrac{1}{3}\times\pi\times 1\times 1\\ \\&=&\dfrac{\pi}{3}\end{array}$

donc,

$\boxed{V_{\text{cône}}=\dfrac{\pi}{3}\;m^{3}}$

$-\$ volume d'une boule :

On a :

$\begin{array}{rcl} V_{\text{boule}}&=&\dfrac{4}{3}\times\pi\times R^{3}\\ \\&=&\dfrac{4}{3}\times\pi\times 1\\ \\&=&\dfrac{4\pi}{3}\end{array}$

donc,

$\boxed{V_{\text{boule}}=\dfrac{4\pi}{3}\;m^{3}}$

$-\$ volume d'un cylindre :

On a :

$\begin{array}{rcl} V_{\text{cylindre}}&=&\pi\times R^{2}\times h\\ \\&=&\pi\times 1\times 1\\ \\&=&\pi\end{array}$

donc,

$\boxed{V_{\text{cylindre}}=\pi\;m^{3}}$

2) Exprimons le volume d'une boule et celui d'un cylindre en fonction du volume d'un cône de révolution pour

$R=h.$

On a :

$V_{\text{cône}}=\dfrac{1}{3}\times\pi\times R^{2}\times h$ or,

$R=h$

donc,

$V_{\text{cône}}=\dfrac{1}{3}\times\pi\times R^{3}$

on aura alors :

$\pi\times R^{3}=3\times V_{\text{cône}}$

On a :

$V_{\text{boule}}=\dfrac{4}{3}\times\pi\times R^{3}$ or,

$\pi\times R^{3}=3\times V_{\text{cône}}$

donc,

$\begin{array}{rcl} V_{\text{boule}}&=&\dfrac{4}{3}\times 3\times V_{\text{cône}}\\ \\&=&4\times V_{\text{cône}}\end{array}$

ainsi,

$\boxed{V_{\text{boule}}=4\times V_{\text{cône}}}$

On a :

$V_{\text{cylindre}}=\pi\times R^{2}\times h$ or,

$R=h$

donc,

$V_{\text{cylindre}}=\pi\times R^{3}$

comme

$\pi\times R^{3}=3\times V_{\text{cône}}$ alors,

$V_{\text{cylindre}}=3\times V_{\text{cône}}$

d'où,

$\boxed{V_{\text{cylindre}}=3\times V_{\text{cône}}}$

3) Exprimons le volume de ce récipient en fonction du volume du cylindre.

On a :

$V_{\text{récipient}}=V_{\text{cylindre}}-V_{\text{cône}}$

or, on sait que

$V_{\text{cylindre}}=3\times V_{\text{cône}}$

c'est-à-dire,

$V_{\text{cône}}=\dfrac{1}{3}V_{\text{cylindre}}$

donc,

$\begin{array}{rcl} V_{\text{récipient}}&=&V_{\text{cylindre}}-V_{\text{cône}}\\ \\&=&V_{\text{cylindre}}-\dfrac{1}{3}V_{\text{cylindre}}\\ \\&=&\dfrac{2}{3}V_{\text{cylindre}}\end{array}$

ainsi,

$\boxed{V_{\text{récipient}}=\dfrac{2}{3}V_{\text{cylindre}}}$

Auteur:

Diny Faye