Mouvement d'une particule chargée dans un champ électrostatique E uniforme - Ts

 

Une particule chargée de masse $m$ et de charge $q>0$ est lancée avec un vecteur vitesse $\vec{v}_{0}$, dans une région de l'espace où règne un champ électrostatique $\vec{E}$ uniforme $(\vec{E}\perp\vec{v}_{0}).$

 

Étudier le mouvement de la particule.

Le système est constitué de la particule assimilable à un point matériel et le référentiel d'étude est le référentiel terrestre considéré comme galiléen.

 

Les forces extérieures appliquées à la particule sont la force électrostatique $\vec{F}=q.\vec{E}$ et son poids $\vec{p}=m.\vec{g}$ qui est négligeable par rapport à $\vec{F}.$

 

En appliquant la deuxième loi de Newton, on a : $$\sum \vec{F}_{\text{ext}}=m\vec{a}$$

 

Soit : $$\vec{F}+\vec{p}=m.\vec{a}$$

 

Le poids étant négligeable alors, on obtient : $$\vec{F}=m.\vec{a}$$ 

 

Soit : $$q.\vec{E}=m.\vec{a}$$

 

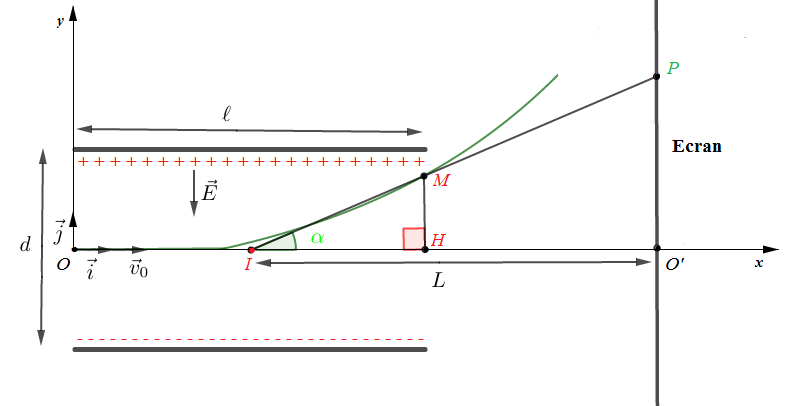
Choisissons comme repère de projection, le repère $(O\;;\ \vec{i}\;,\ \vec{j})$ et supposons qu'à l'instant initial $t_{0}=0$, la particule se trouve au point $O$, origine du repère.

Projetons la relation vectorielle $q.\vec{E}=m.\vec{a}$ suivant les axes du repère. 

 

Soit les vecteurs $\vec{E}\begin{pmatrix} E_{x}=0\\E_{y}=-E\end{pmatrix}\ $ et $\ \vec{a}\begin{pmatrix} a_{x}\\a_{y}\end{pmatrix}$ alors, on a : 

 

$-\ \ $ Suivant l'axe $Ox$

 

$q.E_{x}=m.a_{x}\ $ or, $E_{x}=0$ donc, $a_{x}=0.$

 

Par suite, $v_{x}=\text{cst}$ car $a_{x}=\dfrac{\mathrm{d}v_{x}}{\mathrm{d}t}$

 

Or, à $t_{0}=0\;,\ v_{x}=v_{0_{x}}=v_{0}=\text{cst}.$

 

D'où :  $$\boxed{v_{x}=v_{0}}$$

 

Par ailleurs, $v_{x}=\dfrac{\mathrm{d}x}{\mathrm{d}t}\ \Rightarrow\ \mathrm{d}x=v_{x}\mathrm{d}t=v_{0}\mathrm{d}t$

 

D'où, après intégration ou par passages aux primitives, on obtient : $$x=v_{0}t+x_{0}$$

 

Or, à $t_{0}=0\;,\ x_{0}=0\;,\ y_{0}=0$

 

Par suite, $$\boxed{x=v_{0}t}$$

 

$-\ \ $ Suivant l'axe $Oy$

 

$q.E_{y}=m.a_{y}\ $ or, $E_{y}=-E$ donc, $a_{y}=-\dfrac{q.E}{m}.$

 

Par ailleurs, $\ a_{y}=\dfrac{\mathrm{d}v_{y}}{\mathrm{d}t}\ \Leftrightarrow\ \mathrm{d}v_{y}=a_{y}\mathrm{d}t=-\dfrac{q.E}{m}\mathrm{d}t$

 

Ce qui donne, après intégration ou par passage aux primitives : $$v_{y}=-\dfrac{q.E}{m}t+v_{0_{y}}$$

 

Or, à $t_{0}=0\;,\ v_{0_{y}}=0.$

 

D'où : $$\boxed{v_{y}=-\dfrac{q.E}{m}t}$$

 

Par ailleurs, on a : 

 

$\begin{array}{rcl} v_{y}=\dfrac{\mathrm{d}y}{\mathrm{d}t}\ \Rightarrow\ \mathrm{d}y&=&v_{y}\mathrm{d}t\\ \ \Rightarrow\ \mathrm{d}y&=&-\dfrac{q.E}{m}t\mathrm{d}t\end{array}$

 

L'intégration de cette dernière expression de $(\mathrm{d}y)$ donne : $$y=-\dfrac{1}{2}\dfrac{q.E}{m}t^{2}+y_{0}$$

 

Comme à $t_{0}=0\;,\ x_{0}=0\;,\ y_{0}=0$ alors, $$\boxed{y=-\dfrac{1}{2}\dfrac{q.E}{m}t^{2}}$$

 

Les équations horaires du mouvement sont alors données par : $$\boxed{\begin{array}{rcl} x&=&v_{0}t\\ \\y&=&-\dfrac{1}{2}\dfrac{q.E}{m}t^{2}\end{array}}\qquad\begin{array}{l} (1)\\ \\(2)\end{array}$$

L'équation de la trajectoire $y=f(x)$ est obtenue en éliminant le temps $t$ entre les équations horaires (1) et (2).

 

De l'équation (1), on tire : $t=\dfrac{x}{v_{0}}$

 

En remplaçant cette expression de $t$ dans l'équation (2), on obtient : 

 

$\begin{array}{rcl} y&=&-\dfrac{1}{2}\dfrac{q.E}{m}t^{2}\\\\&=&-\dfrac{1}{2}\dfrac{q.E}{m}\left(\dfrac{x}{v_{0}}\right)^{2}\\ \\&=&-\dfrac{1}{2}\dfrac{q.E.x^{2}}{m.v_{0}^{2}}\end{array}$

 

D'où, l'équation de la trajectoire donnée par : $$\boxed{y=-\dfrac{1}{2}\dfrac{q.E.x^{2}}{m.v_{0}^{2}}}\qquad(3)$$

 

On reconnait alors l'équation d'une parabole d'axe vertical.

 

D'où, la trajectoire est une parabole.

La particule sortira du champ électrostatique lorsque sa trajectoire ne rencontre pas les plaques.

 

A la limite de sortie, la particule est au point $M.$

 

Soit $H$ le projeté orthogonal de $M$ sur l'axe $Ox$ et soit $I$ milieu du segment $[OH].$

 

Ainsi, la particule sortira du champ si, et seulement si, $$MH<\dfrac{d}{2}$$

 

$d$ étant la distance entre les deux plaques.

 

On a : 

 

$\begin{array}{rcl} MH&=&\sqrt{(x_{_{H}}-x_{_{M}})^{2}+(y_{_{H}}-y_{_{M}})^{2}}\\\\&=&\sqrt{(\ell-\ell)^{2}+(0-y_{_{M}})^{2}}\\ \\&=&\sqrt{y_{_{M}}^{2}}\\ \\&=&|y_{_{M}}|\\ \\ &=&\left|-\dfrac{1}{2}\dfrac{q.E.x_{_{M}}^{2}}{m.v_{0}^{2}}\right|\\ \\&=&\dfrac{1}{2}\dfrac{q.E.\ell^{2}}{m.v_{0}^{2}}\end{array}$

 

Par suite, 

 

$\begin{array}{rcl} MH<\dfrac{d}{2}&\Leftrightarrow&\dfrac{1}{2}\dfrac{q.E.\ell^{2}}{m.v_{0}^{2}}<\dfrac{d}{2}\\ \\&\Leftrightarrow&m.v_{0}^{2}.d>q.E.\ell^{2}\\ \\ &\Leftrightarrow&v_{0}^{2}>\dfrac{q.E.\ell^{2}}{m.d}\\ \\&\Leftrightarrow&v_{0}>\sqrt{\dfrac{q.E.\ell^{2}}{m.d}}\end{array}$

 

D'où, $$\boxed{v_{0}>\sqrt{\dfrac{q.E.\ell^{2}}{m.d}}}\qquad(4)$$

 

Ainsi, pour une telle vitesse $v_{0}$, la particule va sortir du champ sans heurter la plaque.

 

Dès la sortie, le mouvement sera rectiligne uniforme car la particule n'est plus soumise à une force électrostatique.

 

Remarque 

 

Comme $E=\dfrac{u}{d}$ alors, la condition de sortie peut encore s'écrire : $v_{0}>\dfrac{\ell}{d}\sqrt{\dfrac{q.u}{m}}.$

Soit $\alpha$ l'angle de déviation de la particule alors, on a : $$\tan\alpha=\dfrac{MH}{IH}$$

 

Or, $\dfrac{1}{2}\dfrac{q.E.\ell^{2}}{m.v_{0}^{2}}\ $ et $\ IH=\dfrac{\ell}{2}$

 

Par suite, 

 

$\begin{array}{rcl} \tan\alpha&=&\dfrac{MH}{IH}\\\\&=&\dfrac{\dfrac{1}{2}\dfrac{q.E.\ell^{2}}{m.v_{0}^{2}}}{\dfrac{\ell}{2}}\\ \\&=&\dfrac{q.E.\ell^{2}}{\ell.m.v_{0}^{2}}\\ \\&=&\dfrac{q.E.\ell}{m.v_{0}^{2}}\end{array}$

 

D'où, $$\boxed{\tan\alpha=\dfrac{q.E.\ell}{m.v_{0}^{2}}}\qquad(5)$$

La déflexion électrique est la distance $O'P.$ Elle est donc déterminée en localisant le point d'impact de la particule sur l'écran.

 

On a : $\tan\alpha=\dfrac{O'P}{IO'}\ \Rightarrow\ O'P=IO'.\tan\alpha\ $ or, $IO'=L.$ 

 

Par suite, $O'P=L.\tan\alpha$

 

D'où, $$\boxed{O'P=L.\dfrac{q.E.\ell}{m.v_{0}^{2}}}\qquad(6)$$