Gravitation universelle - Ts
Classe:
Terminale
I. Force gravitationnelle (Loi de Newton)
Soit les masses $m_{_{A}}$ et $m_{_{B}}$ de deux particules placées respectivement en $A$ et $B$ et séparées d'une distance $r$, les forces d'interaction gravitationnelle entre $m_{_{A}}$ et $m_{_{B}}$, notées $\vec{F}_{_{A/B}}$ et $\vec{F}_{_{B/A}}$, sont attractives, proportionnelles au produit des masses et inversement proportionnelles au carré de la distance qui les sépare.
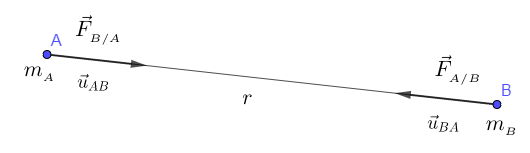
$\vec{F}_{_{A/B}}$ est la force d'attraction de $A$ sur $B$, dirigée de $B$ vers $A$
$\vec{F}_{_{B/A}}$ est la force d'attraction exercée par $B$ sur $A$, dirigée de $A$ vers $B$
Ces deux forces ont la même direction, celle de la droite $(AB).$
De plus, On a :
$\begin{array}{rcl} \vec{F}_{_{A/B}}&=&-\dfrac{\mathcal{G}.m_{_{A}}.m_{_{B}}}{r^{2}}\vec{u}_{_{AB}}\quad\text{or }\ \vec{u}_{_{AB}}=-\vec{u}_{_{BA}}\\ \\&=&-\left(-\dfrac{\mathcal{G}.m_{_{A}}.m_{_{B}}}{r^{2}}\vec{u}_{_{BA}}\right)\\ \\&=&-\vec{F}_{_{B/A}}\end{array}$
D'où, $$\vec{F}_{_{A/B}}=-\vec{F}_{_{B/A}}$$
Ainsi, $\vec{F}_{_{A/B}}$ et $\vec{F}_{_{B/A}}$ sont de sens opposé.
L'intensité de ces forces, exprimée en Newton (N), est donnée par : $$\boxed{F_{_{A/B}}=F_{_{B/A}}=\dfrac{\mathcal{G}.m_{_{A}}.m_{_{B}}}{r^{2}}}\qquad(1)$$ où, $\ \mathcal{G}=6.67\;10^{-11}\;N.m^{2}.kg^{-2}$ est la constante de gravitation universelle.
Exemple
Soit $m_{1}$ et $m_{2}$ deux masses de deux particules distantes de $r.$
Déterminer la force d'interaction gravitationnelle entre ces deux particules.
On donne : $m_{1}=25\;kg\;,\quad m_{2}=75\;,kg\;,\quad r=100\;m$
Résolution
En appliquant la loi de l'attraction gravitationnelle, on obtient : $$F_{_{1/2}}=F_{_{2/1}}=\dfrac{\mathcal{G}.m_{_{1}}.m_{_{2}}}{r^{2}}$$
A.N : $F_{_{1/2}}=F_{_{2/1}}=\dfrac{6.67\;10^{-11}\times 25\times 75}{100^{2}}=1.25\;10^{-11}$
D'où, $\boxed{F_{_{1/2}}=F_{_{2/1}}=1.25\;10^{-11}\;N}$
Remarque
L'interaction gravitationnelle s'applique aussi aux corps non ponctuels à symétrie sphérique dont la masse reste concentrée autour de leur centre d'inertie.
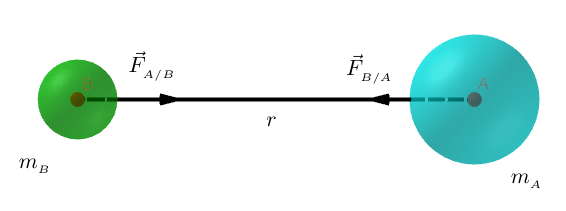
Exemple
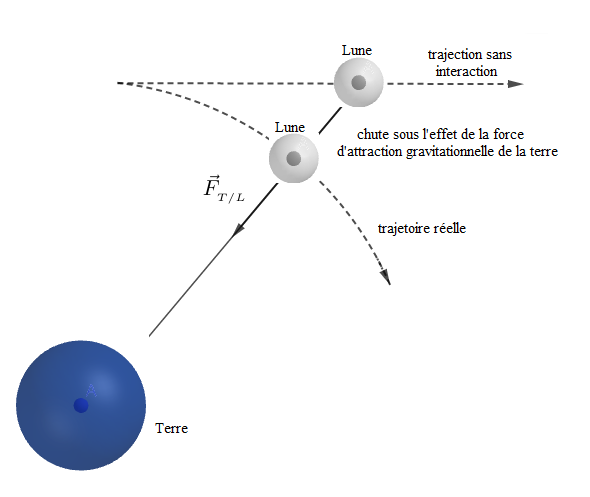
La force d'attraction gravitationnelle exercée par la terre de masse $m_{_{T}}=5.97\;10^{24}\;kg$ sur la lune de masse $m_{_{L}}=7.35\;10^{22}\;kg$, séparée d'une distance $r=3.83\;10^{5}\;km$, a pour intensité : $$F_{_{T/L}}=\dfrac{\mathcal{G}.m_{_{T}}.m_{_{L}}}{r^{2}}$$
A.N : $F_{_{T/L}}=\dfrac{6.67\;10^{-11}\times 5.97\;10^{24}\times 7.35\;10^{22}}{(3.83\;10^{8})^{2}}=2\;10^{20}$
Ainsi, $\boxed{F_{_{T/L}}=2\;10^{20}\;N}$
Sans cette force, la trajectoire de la lune serait rectiligne uniforme. C'est donc cette force d'attraction qui entraîne continuellement la lune dans un mouvement autour de la terre en modifiant sa trajectoire. D'où, l'appellation de force de gravitation.
Remarque
La loi de l'attraction gravitationnelle est un phénomène universel lié à la présence de la matière (masse). Ses effets sont beaucoup mieux perceptibles entre les astres que entre des objets sur terre.
II. Champ de gravitation $\vec{G}$
II.1 Définition
Dans une région de l'espace où règne un champ gravitationnel, en y plaçant une masse $m$, celle-ci est soumise à une fore gravitationnelle $\vec{F}$ définie par : $$\vec{F}=m.\vec{G}$$
$\vec{G}$ est appelé champ de gravitation exprimé en $N.kg^{-1}\ $ ou en $\ N.s^{-2}$
Remarque
$\vec{F}\ $ et $\ \vec{G}$ sont toujours de même sens.
II.2. Champ gravitationnel créé par une masse ponctuelle
Calculons le champ de gravitation créé par une masse ponctuelle $m$ en un point $A$ situé à une distance de $r$ mètres.
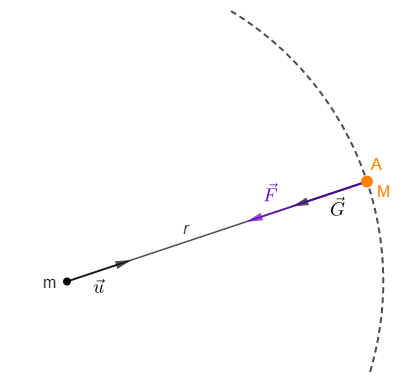
La masse $M$ placée au point $A$ est soumise à une fore gravitationnelle $\vec{F}$ telle que $\vec{F}=M.\vec{G}$
Or, d'après la loi de l'attraction gravitationnelle, $\vec{F}=-\dfrac{\mathcal{G}.m.M}{r^{2}}\vec{u}.$
Donc, $M.\vec{G}=-\dfrac{\mathcal{G}.m.M}{r^{2}}\vec{u}$
Par suite, $\vec{G}=-\dfrac{\mathcal{G}.m}{r^{2}}\vec{u}$
D'où, $$\boxed{G=\dfrac{\mathcal{G}.m}{r^{2}}}\qquad(2)$$
II.3. Champ de gravitation créé par un corps sphérique (une masse non ponctuelle)
Considérons un corps sphérique de rayon $R$ de masse totale $M$ et soit une masse $m$ placée en un point $A$ de l'espace.
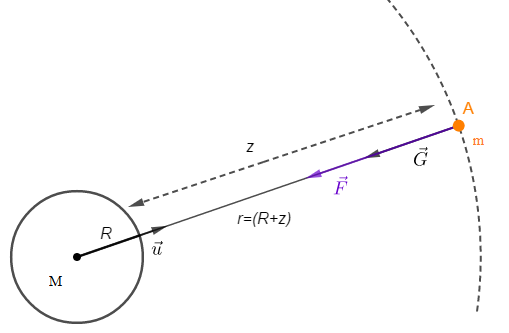
Comme l'interaction gravitationnelle s'applique aussi aux corps non ponctuels à symétrie sphérique alors, le champ de gravitation créé par ce corps sphérique est donné par : $$\vec{G}=-\dfrac{\mathcal{G}.M}{r^{2}}\vec{u}$$
Or, $r=R+z$ donc, $$\vec{G}=-\dfrac{\mathcal{G}.M}{(R+z)^{2}}\vec{u}$$
D'où, $$\boxed{G=\dfrac{\mathcal{G}.M}{(R+z)^{2}}}\qquad(3)$$
II.3. Champ de gravitation créé par la terre
La terre étant un corps sphérique alors, son champ de gravitation sera donné par : $$G_{_{T}}=\dfrac{\mathcal{G}.M_{_{T}}}{(R_{_{T}}+z)^{2}}$$
$\centerdot\ \ $ A la surface de la terre, on a : $z=0$ donc, $$\boxed{G_{_{T}}=G_{0}=\dfrac{\mathcal{G}.M_{_{T}}}{R_{_{T}}^{2}}}$$
avec $M_{_{T}}=5.97\;10^{24}\;kg\;,\ R_{_{T}}=64\;10^{5}\;m$
A.N : $G_{0}=\dfrac{6.67\;10^{-11}\times 5.97\;10^{24}}{(64\;10^{5})^{2}}=9.82$
D'où, $\boxed{G_{0}=9.82\;N.kg^{-1}\simeq g}$
$\centerdot\ \ $ Au voisinage de la terre ; c'est-à-dire pour $z$ très petit devant $R_{_{T}}$, on a :
$\begin{array}{rcl} G_{_{T}}=G_{z}&=&\dfrac{\mathcal{G}.M_{_{T}}}{(R_{_{T}}+z)^{2}}\\ \\&=&\dfrac{\mathcal{G}.M_{_{T}}}{(R_{_{T}}+z)^{2}}\times\dfrac{R_{_{T}}^{2}}{R_{_{T}}^{2}}\quad\text{or }\ G_{0}=\dfrac{\mathcal{G}.M_{_{T}}}{R_{_{T}}^{2}}\\ \\&=&G_{0}.\dfrac{R_{_{T}}^{2}}{(R_{_{T}}+z)^{2}}\\ \\&=&G_{0}\left(\dfrac{R_{_{T}}}{R_{_{T}}\left(1+\dfrac{z}{R_{_{T}}}\right)}\right)^{2}\\ \\&=&G_{0}\left(1+\dfrac{z}{R_{_{T}}}\right)^{-2}\end{array}$
D'après cours de mathématiques, la fonction $(1+x)^{\alpha}$ peut être approchée par $1+\alpha x$, au voisinage de 0 ; c'est-à-dire lorsque $x$ est très petit $(x\ll 1).$
Ainsi, en appliquent cette formulation à l'expression $\left(1+\dfrac{z}{R_{_{T}}}\right)^{-2}$ où $\dfrac{z}{R_{_{T}}}$ est très petit par rapport à 1 du fait que $z\ll R_{_{T}}$, on obtient : $$\left(1+\dfrac{z}{R_{_{T}}}\right)^{-2}=1-\dfrac{2z}{R_{_{T}}}$$
D'où, $$\boxed{G_{z}=G_{0}\left(1-\dfrac{2z}{R_{_{T}}}\right)}$$
III. Champ de gravitation $\vec{G}$ - Champ de pesanteur $\vec{g}$
Le poids $\vec{P}$ d'un objet de masse $m$, situé dans l'environnement terrestre et soumis à l'attraction gravitationnelle de la terre, est approximativement identique à la force d'attraction gravitationnelle $\vec{F}_{_{\text{Terre/Objet}}}$ exercée par la terre sur cet objet.
On a : $\vec{F}_{_{\text{Terre/Objet}}}=\vec{P}\ \Rightarrow\ m.\vec{G}=m.\vec{g}$
Soit : $$\vec{G}=\vec{g}$$
D'où, pour un objet situé à une altitude, $z$, de la terre : $$g_{_{T}}=\dfrac{\mathcal{G}.M_{_{T}}}{(R_{_{T}}+z)^{2}}$$
Par conséquent, à la surface de la terre $(z=0)$, on obtient : $$g_{_{T}}=\dfrac{\mathcal{G}.M_{_{T}}}{R_{_{T}}^{2}}\approx 9.81\;N.kg^{-1}$$
Par analogie, la pesanteur, $g_{_{L}}$, au niveau de la lune est donnée par : $$g_{_{L}}=\dfrac{\mathcal{G}.M_{_{L}}}{R_{_{L}}^{2}}$$
avec $M_{_{L}}=7.35\;10^{22}\;kg\;,\ R_{_{L}}=1737.4\;km$
A.N : $g_{_{L}}=\dfrac{6.67\;10^{-11}\times 7.35\;10^{22}}{(1737.4\;10^{3})^{2}}=1.62$
D'où, $$\boxed{g_{_{L}}=1.62\;N.kg^{-1}}$$
Exemple
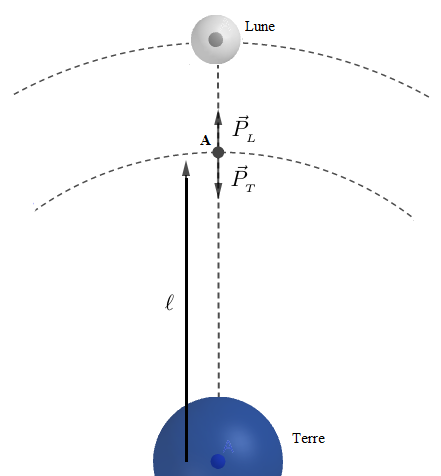
Soit une masse $m$ placée en un point $A$ équigravitationnel entre la terre et la lune.
A quelle distance $\ell$ de la terre se trouve alors la masse $m\ ?$
Données : $M_{_{T}}=5.97\;10^{24}\;kg\;,\ M_{_{L}}=7.35\;10^{22}\;kg\;,\ d=3.83\;10^{5}\;km$
Résolution
Au point équigravitationnel, on a : $$\vec{P}_{_{T}}+\vec{P}_{_{L}}=\vec{0}\ \Rightarrow\ \vec{g}_{_{T}}=-\vec{g}_{_{L}}$$
Soit alors, $$g_{_{T}}=g_{_{L}}$$
Soit $d$ la distance entre la terre et la lune.
Donc, si $\ell$ est la distance entre le point $A$ et le centre de la terre alors, $d-\ell$ sera la distance entre ce même point $A$ et le centre de la lune.
On a :
$\begin{array}{rcl} g_{_{T}}=g_{_{L}}&\Leftrightarrow&\dfrac{\mathcal{G}.M_{_{T}}}{\ell^{2}}=\dfrac{\mathcal{G}.M_{_{L}}}{(d-\ell)^{2}}\\ \\&\Leftrightarrow&\dfrac{M_{_{T}}}{\ell^{2}}=\dfrac{M_{_{L}}}{(d-\ell)^{2}}\\ \\&\Leftrightarrow&\dfrac{M_{_{T}}}{M_{_{L}}}=\dfrac{\ell^{2}}{(d-\ell)^{2}}\\ \\&\Leftrightarrow&\dfrac{\ell}{(d-\ell)}=\sqrt{\dfrac{M_{_{T}}}{M_{_{L}}}}\\ \\&\Leftrightarrow&\ell=(d-\ell)\sqrt{\dfrac{M_{_{T}}}{M_{_{L}}}}\\ \\&\Leftrightarrow&\ell\left(1+\sqrt{\dfrac{M_{_{T}}}{M_{_{L}}}}\right)=d.\sqrt{\dfrac{M_{_{T}}}{M_{_{L}}}}\\ \\&\Leftrightarrow&\ell=\dfrac{d.\sqrt{\dfrac{M_{_{T}}}{M_{_{L}}}}}{\left(1+\sqrt{\dfrac{M_{_{T}}}{M_{_{L}}}}\right)}\end{array}$
Donc, $$\boxed{\ell=\dfrac{d.\sqrt{\dfrac{M_{_{T}}}{M_{_{L}}}}}{\left(1+\sqrt{\dfrac{M_{_{T}}}{M_{_{L}}}}\right)}}$$
A.N : $\ell=\dfrac{3.83\;10^{8}\times\sqrt{\dfrac{5.97\;10^{24}}{7.35\;10^{22}}}}{1+\sqrt{\dfrac{5.97\;10^{24}}{7.35\;10^{22}}}}=3.45\;10^{8}\;m$
D'où, $\boxed{\ell=3.45\;10^{5}\;km}$

A cette distance $\ell$, de la terre, la masse $m$ reste en équilibre entre la terre et la lune.
C'est le même phénomène qui se produit avec les satellites qui doivent se libérer de la pesanteur terrestre pour se mettre sur orbite.

Commentaires
DoulayePro (non vérifié)
lun, 03/29/2021 - 15:44
Permalien
Suggestions
Anonyme (non vérifié)
mer, 12/29/2021 - 18:01
Permalien
merci
Ajouter un commentaire