Vous êtes ici

Solution des exercices : Énergie potentiel - Énergie mécanique - 1 er s

Classe:

Première

Exercice 1

1) Énergie mécanique (énergie totale) du chariot au point

$A$

$E_{m_{A}}=E_{C_{A}}+E_{p_{A}}$

$E_{p}(z)=mgz+cte$

Considérons l'état de référence l'origine

$O$ des cotes

Alors,

$\begin{array}{rcl} E_{p}(z=0)&=&mg\times0+cte\\&=&0\end{array}$

$E_{p}(z)=mgz\;,\ E_{p_{A}}=mgz_{A}\$ et

$\ E_{c_{A}}=\dfrac{1}{2}mv_{A}^{2}$

Ainsi,

$\begin{array}{rcl} E_{m_{A}}&=&\dfrac{1}{2}mv_{A}^{2}+mgz_{A}\\ \\&=&\dfrac{1}{2}\times 1000.0\times 1.80^{2}+1000.0\times10\times30.0\\ \\&=&3.02\cdot 10^{5}\end{array}$

D'où,

$\boxed{E_{m_{A}}=3.02\cdot 10^{5}\;J}$

2) Vitesse du chariot au point

$B$

Le système est conservatif, la conservation de l'énergie mécanique s'écrit :

$\begin{array}{rcl} E_{m_{B}}=E_{m_{A}}&\Rightarrow&\dfrac{1}{2}mv_{B}^{2}+mgz_{B}=E_{m_{A}}\\ \\&\Rightarrow&\dfrac{1}{2}mv_{B}^{2}+0=E_{m_{A}}\\ \\&\Rightarrow&v_{B}^{2}=\dfrac{2E_{m_{A}}}{m}\\ \\&\Rightarrow&v_{B}=\sqrt{\dfrac{2E_{m_{A}}}{m}}\end{array}$

A.N :

$v_{B}=\sqrt{\dfrac{2\times 3.02\;10^{5}}{1000}}=24.6$

D'où,

$\boxed{v_{B}=24.6\;m\cdot s^{-1}}$

3) Énergie potentielle et énergie cinétique du chariot au point

$C$

$\begin{array}{lcl} E_{p_{C}}&=&mgz_{C}\\ \\&=&1000\times10\times25.0\\ \\&=&2.50\cdot 10^{5}\end{array}$

Ainsi,

$\boxed{E_{p_{C}}=2.50\cdot 10^{5}\;J}$

$\begin{array}{rcl} E_{p_{C}}+E_{c_{C}}=E_{m_{C}}&\Rightarrow&E_{c_{C}}=E_{m_{C}}-E_{p_{C}}\quad\text{or, }\ E_{m_{C}}=E_{m_{A}}\\ \\&\Rightarrow&E_{c_{C}}=E_{m_{A}}-E_{p_{C}}\\ \\&\Rightarrow&E_{c_{C}}=3.02\cdot 10^{5}-2.50\cdot 10^{5}\\ \\&\Rightarrow&E_{c_{C}}=5.2\cdot 10^{4}\end{array}$

D'où,

$\boxed{E_{c_{C}}=5.2\cdot 10^{4}\;J}$

4) Vitesse du chariot au point

$D$

$\begin{array}{rcl} E_{m_{D}}=E_{p_{D}}+E_{c_{D}}&\Rightarrow&mgz_{D}+\dfrac{1}{2}mv_{D}^{2}=E_{m_{D}}\quad\text{or, }\ E_{m_{D}}=E_{m_{C}}\\ \\&\Rightarrow&mgz_{D}+\dfrac{1}{2}mv_{D}^{2}=E_{m_{C}}\\ \\&\Rightarrow&mv_{D}^{2}=\dfrac{2(E_{m_{C}}-mgz_{D})}{m}\\ \\&\Rightarrow&v_{D}=\sqrt{\dfrac{2(E_{m_{C}}-mgz_{D})}{m}}\end{array}$

A.N :

$v_{D}=\sqrt{\dfrac{2(3.02\cdot10^{5}-1000\times10\times12.0)}{1000}}=9.92$

D'où,

$\boxed{v_{D}=9.92\;m\cdot s^{-1}}$

Exercice 2

1. Calcul de :

$-\$ l'énergie potentielle de pesanteur de la pierre dans sa position la plus haute

$-\$ l'énergie potentielle de pesanteur de la pierre dans sa position la plus basse

$-\$ la variation d'énergie potentielle de la pierre

1.1 Lorsque l'on choisit comme niveau de référence le niveau du point de lancement de la pierre

$\begin{array}{rcl} E_{p}(Z)=mgz+cte&\Rightarrow&E_{p}(Z=0)=mg\times 0+cte\quad\text{or, }\ E_{p}(Z=0)=0\\ \\&\Rightarrow&cte=0\\ \\&\Rightarrow&E_{p}(Z)=mgz\end{array}$

Par suite,

$E_{p}(Z_{H})=mgz_{H}$

A.N :

$E_{p}(Z_{H})=70\times10\times10\ \Rightarrow\ E_{p}(Z_{H})=7.0\cdot 10^{3}$

Ainsi,

$\boxed{E_{p}(Z_{H})=7.0\cdot 10^{3}\;J}$

$E_{p}(Z_{B})=mgz_{B}$

A.N :

$E_{p}(Z_{B})=70\times10\times -2.0=-14\cdot 10^{2}$

D'où,

$\boxed{E_{p}(Z_{B})=-14\cdot 10^{2}\;J}$

$\Delta\,E_{p}=E_{p}(z_{B})-E_{p}(z_{H})$

A.N :

$\Delta\,E_{p}=-14\cdot 10^{2}-7.0\cdot 10^{3}=-84\cdot 10^{2}$

Ainsi,

$\boxed{\Delta\,E_{p}=-84\cdot 10^{2}\;J}$

1.2 Lorsque Lorsque l'on choisit comme niveau de référence le niveau de la surface de l'eau.

$\begin{array}{rcl} E_{p}(Z)=mgz+cte&\Rightarrow&E_{p}(Z_{eau})=mgz_{eau}+cte\quad\text{or, }\ E_{p}(Z_{eau})=0\\ \\&\Rightarrow&cte=-(70\times10\times (-2.0)\\ \\&\Rightarrow&cte=14\cdot 10^{2}\;J\end{array}$

Donc,

$E_{p}(z)=mgz+14\cdot 10^{2}$

Par suite,

$E_{p}(z_{H})=mgz_{H}+14\cdot 10^{2}$

A.N :

$E_{p}(z_{H})=70\times 10\times 10+14\cdot 10^{2}=84\cdot 10^{2}$

D'où,

$E_{p}(z_{H})=84\cdot 10^{2}\;J$

Soit

$E_{p}(z_{B})=0\;J$ alors,

$\Delta\,E_{p}=E_{p}(z_{B})-E_{p}(z_{H})$

A.N :

$\Delta\,E_{p}=0-7.0\cdot 10^{3} =-7.0\cdot 10^{3}$

Ainsi,

$\boxed{\Delta\,E_{p}=0-7.0\cdot 10^{3} =-7.0\cdot 10^{3}\;J}$

2. Expression énergie potentielle de pesanteur de la pierre lorsqu'elle est située à une altitude

$z$ quelconque

$E_{P}(z)=mgz$

$E_{p}(z)=mgz+14\cdot 10^{2}$

Exercice 3

1. Expression littérale de l'énergie potentielle du skieur en

$A.$

$E_{p}(z)=mgz+cte$

Alors,

$E_{p}(Z_{B})=mgz_{B}+cte\$ or,

$\ E_{p}(Z_{B})=0$

Donc,

$\begin{array}{rcl} mgz_{B}+cte=0&\Rightarrow&mg\times 0+cte=0\\ \\&\Rightarrow&cte=0\\ \\&\Rightarrow&E_{p}(z)=mgz\end{array}$

Ainsi,

$E_{p_{A}}(Z)=mgz_{A}\$ or,

$\ z_{A}=\mathrm{d}\sin\alpha$

Par suite,

$E_{p_{A}}(z)=mg\mathrm{d}\sin\alpha$

A.N :

$E_{p_{A}}(z)=115\times 10\times 10^{3}\times\sin 26.0^{\circ}=5.0\cdot 10^{5}$

D'où,

$\boxed{E_{p_{A}}(z)=5.0\cdot 10^{5}\;J}$

2. Expression littérale de l'énergie cinétique du skieur en

$B.$

Le système est conservatif, la conservation de l'énergie mécanique s'écrit :

$E_{c_{B}}=\dfrac{1}{2}mv_{B}^{2}$

A.N :

$E_{c_{B}}=\dfrac{1}{2}\times115\times 50.5^{2}=1.5\cdot 10^{5}$

D'où,

$\boxed{E_{c_{B}}=1.5\cdot 10^{5}\;J}$

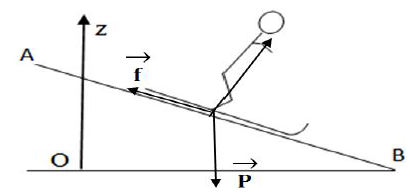
3. Nommons les forces appliquées au système

$\{\text{skieur + équipement}\}$ et représentons les sur un schéma.

Les forces qui exercent sur le système sont :

$\vec{P}\;;\ \vec{R}\$ et

$\ \vec{f}$ éventuellement des forces de frottement

4. Expression du travail de chacune de ces forces.

$\begin{array}{rcl} W_{AB}(\vec{P})&=&\overrightarrow{P}\cdot\overrightarrow{AB}\\ \\&=&mg\,AB\sin\alpha\end{array}$

$W_{AB}(\vec{R})=\vec{R}\cdot\overrightarrow{AB}=0\,J\$ car

$\ \vec{R}\perp\overrightarrow{AB}$

$\begin{array}{rcl} W_{AB}(\vec{f})&=&\vec{f}\cdot\overrightarrow{AB}\\ \\&=&-f\times AB\end{array}$

5. Relation liant la variation d'énergie cinétique du système et le travail des différentes forces.

$\begin{array}{lcl} \Delta\,E_{c}&=&E_{c_{B}}-E_{c_{A}}\\\\&=&W_{AB}(\vec{P})+W_{AB}(\vec{R})+W_{AB}(\vec{f}) \end{array}$

6. Sa vitesse au point

$B$

$\begin{array}{rcl} \Delta\,E_{c}&=&E_{c_{B}}-E_{c_{A}}\\\\&=&W_{AB}(\vec{P})+W_{AB}(\vec{R})\end{array}$

Alors,

$\begin{array}{rcrcl}\dfrac{1}{2}mv_{B}^{2}-0=mg\,AB\sin\alpha+0&\Rightarrow&v_{B}^{2}&=&2g\,AB\sin\alpha\\ \\&\Rightarrow&v_{B}&=&\sqrt{2g\,AB\sin\alpha}\end{array}$

A.N :

$v_{B}=\sqrt{2\times 10\times 10^{3}\times\sin 26.0^{\circ}}=93.6$

D'où,

$\boxed{v_{B}=93.6\,m\cdot s^{-1}}$

7. Détermination de la valeur de ces frottements.

$\begin{array}{rcl} \Delta\,E_{c}&=&E_{c_{B}}-E_{c_{A}}\\\\&=&W_{AB}(\vec{P})+W_{AB}(\vec{R})+W_{AB}(\vec{f})\end{array}$

$\Rightarrow\ \dfrac{1}{2}mv_{B}^{2}-0=mg\,AB\sin\alpha+0-f\times AB$

$\Rightarrow\ f\times AB=mg\,AB\sin\alpha+0-\dfrac{1}{2}mv_{B}^{2}$

$\Rightarrow\ f=m\left(g\sin\alpha-\dfrac{v_{B}^{2}}{2AB}\right)$

A.N :

$f=115\left(10\sin 26.0^{\circ}-\dfrac{50.5^{2}}{2\times 10^{3}}\right)=3.8\cdot 10^{2}$

Ainsi,

$\boxed{f=3.8\cdot 10^{2}\;N}$

Exercice 4

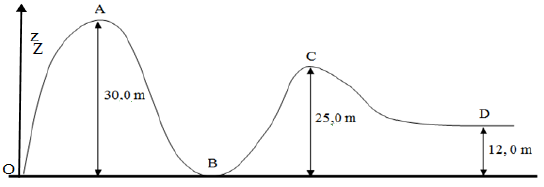
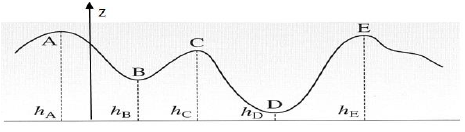
Calcul de la variation d'énergie potentielle de pesanteur du wagonnet passant :

1. de

$A$ à

$B$

Choisissons l'axe

$z$ orienté vers le haut

$E_{p}(z)=mgz+cte$

$\begin{eqnarray} \Delta E_{p} &=& E_{p_{B}}-E_{p_{A}} \nonumber\\\\ &=& mgz_{B}+cte-\left(mgz_{A}+cte\right)\nonumber\\\\ &=& mgz_{B}-mgz_{A} \nonumber\\\\ &=& mg\left(z_{B}-z_{A}\right) \end{eqnarray}$

$\begin{eqnarray} \Delta E_{p} &=& E_{p_{B}}-E_{p_{A}} \nonumber\\\\ &=& mg\left(h_{B}-h_{A}\right)\nonumber\\\\ &=& 65\times 10\times(15-10) \nonumber\\\\ \Rightarrow \Delta E_{p} &=& -65\cdot 10^{2}J \end{eqnarray}$

2. de

$B$ à

$C$

$\begin{eqnarray} \Delta E_{p} &=& E_{p_{C}}-E_{p_{B}} \nonumber\\\\ &=&mg\left(h_{C}-h_{B}\right)\nonumber\\\\ &=&65\times 10\times(15-10)\nonumber\\\\\Rightarrow \Delta E_{p} &=&-65\cdot 10^{2}J \end{eqnarray}$

3. de

$A$ à

$D$

$\begin{eqnarray} \Delta E_{p} &=&E_{p_{D}}-E_{p_{A}} \nonumber\\\\ &=&mg\left(h_{D}-h_{A}\right)\nonumber\\\\ &=&65\times 10\times(5-20)\nonumber\\\\\Rightarrow \Delta E_{p} &=&-97.5\cdot 10^{2}J \end{eqnarray}$

4. de

$A$ à

$E$

$\begin{eqnarray} \Delta E_{p} &=&E_{p_{E}}-E_{p_{A}} \nonumber\\\\ &=&mg\left(h_{E}-h_{A}\right)\nonumber\\\\ &=&65\times 10\times(18-20)\nonumber\\\\\Rightarrow \Delta E_{p} &=&-13\cdot 10^{2}J \end{eqnarray}$

Exercice 8

1. Expression de l'énergie potentielle de pesanteur du solide en en fonction de $m$ , $g$ , et $z$ l'altitude du solide

$E_{p}(z)=mgz+cte$

$\begin{eqnarray} E_{p}(z=0) &=&mg\times 0+cte\nonumber\\\\ &=&0\nonumber\\\\\Rightarrow E_{p} &=&mgz \end{eqnarray}$

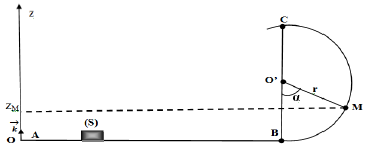
2. Déduction de l'énergie potentielle de pesanteur au point $M$ en fonction de $m$ , $g$ , $r$ , et $\alpha$

$\begin{eqnarray} E_{p_{M}} &=&mgz_{M}\nonumber\\\\\text{or }z_{M} &=&r(1-\cos\alpha)\nonumber\\\\\Rightarrow E_{p_{M}} &=&mgr(1-\cos\alpha) \end{eqnarray}$

3. Pour position $C$ l'énergie potentielle de pesanteur est maximale, car $z_{M}=2r$ la position est maximale.

4. Expression de l'énergie mécanique du solide aux points suivants : $A$ , $B$ et $C$ , sachant que le solide arrive au point $C$ avec une vitesse $v_{C}.$

$\begin{eqnarray} E_{m_{A}} &=&E_{c_{A}}+E_{p_{A}} \nonumber\\\\ &=&\dfrac{1}{2}mv_{A}^{2}+mgz_{A} \nonumber\\\\&=&\dfrac{1}{2}mv_{A}^{2}+0\nonumber\\\\\Rightarrow E_{m_{A}} &=&\dfrac{1}{2}mv_{A}^{2} \end{eqnarray}$

$\begin{eqnarray} E_{m_{B}} &=&E_{c_{B}}+E_{p_{B}} \nonumber\\\\ &=&\dfrac{1}{2}mv_{B}^{2}+mgz_{B} \nonumber\\\\&=&\dfrac{1}{2}mv_{B}^{2}+0\nonumber\\\\\Rightarrow E_{m_{B}} &=&\dfrac{1}{2}mv_{B}^{2} \end{eqnarray}$

$\begin{eqnarray} E_{m_{C}} &=&E_{c_{C}}+E_{p_{C}} \nonumber\\\\ &=&\dfrac{1}{2}mv_{C}^{2}+mgz_{C} \nonumber\\\\&=&\dfrac{1}{2}mv_{C}^{2}+2mgr\nonumber\\\\\Rightarrow E_{m_{C}} &=&\dfrac{1}{2}mv_{C}^{2}+2mgr \end{eqnarray}$

5. Montrons que le solide parcours le périmètre du boucle, on doit avoir $E_{c}(A)>2mgr.$

Les frottements sont négligés, l'énergie mécanique se conserve :

$\begin{eqnarray} E_{m_{A}} &=&E_{m_{C}} \nonumber\\\\ &=&\dfrac{1}{2}mv_{C}^{2}+2mgr \nonumber\\\\\Rightarrow E_{m_{A}} &=& E_{m_{A}}>2mgr \end{eqnarray}$

6. Calcul de la valeur de la vitesse initiale $v_{A}$ pour que le solide arrête au point $C$

$\begin{eqnarray} E_{m_{A}} &=& E_{m_{C}} \nonumber\\\\ &=&\dfrac{1}{2} mv_{C}^{2}+2mgr \nonumber\\\\\text{or }v_{C} &=&0\nonumber\\\\ \Rightarrow E_{m_{A}} &=& E_{c_{A}} \nonumber\\\\ &=&\dfrac{1} {2}mv_{C}^{2}\nonumber\\\\ &=&2mgr\nonumber\\\\\Rightarrow v_{C}^{2} &=&4gr\nonumber\\\\\Rightarrow v_{C} &=&\sqrt{4gr}\nonumber\\\\ &=&\sqrt{4\times 10\times 1.5}\nonumber\\\\\Rightarrow v_{C} &=&7.7\,m\cdot s^{-1} \end{eqnarray}$

Auteur:

Sidy Mouhamed Ndiaye

Commentaires

Anonyme (non vérifié)

mar, 05/12/2020 - 03:56

Vous êtes ici

Solution des exercices : Énergie potentiel - Énergie mécanique - 1 er s

Formulaire de recherche

Exercice 1

Exercice 2

Exercice 3

Exercice 4

Exercice 8

Commentaires

Pages

Ajouter un commentaire

Plain text