Corrigé BFEM maths 2012
Exercice 1
1) Soit : $t=\sqrt{45}+\sqrt{196}-\sqrt{180}-\sqrt{245}$
Écrivons $t$ sous la forme $a\sqrt{b}+c$ où $a\;,\ b\ $ et $\ c$ sont des entiers ; $b$ étant le plus petit entier positif possible.
On a :
$\begin{array}{rcl} t&=&\sqrt{45}+\sqrt{196}-\sqrt{180}-\sqrt{245}\\ \\&=&\sqrt{9\times 5}+\sqrt{4\times 49}-\sqrt{36\times 5}-\sqrt{49\times 5}\\ \\&=&\sqrt{9}\times\sqrt{5}+\sqrt{4}\times\sqrt{49}-\sqrt{36}\times\sqrt{5}-\sqrt{49}\times\sqrt{5}\\ \\&=&3\sqrt{5}+2\times 7-6\sqrt{5}-7\sqrt{5}\\ \\&=&-10\sqrt{5}+14\end{array}$
Donc, $\boxed{t=-10\sqrt{5}+14}$
D'où, $a=-10\;,\ b=5\ $ et $\ c=14$
2) On donne les réels $x=\dfrac{4}{7+3\sqrt{5}}\ $ et $\ y=3\sqrt{5}-7$
a) Écrivons $x$ avec un dénominateur rationnel.
Pour cela, on multiplie le numérateur et le dénominateur par l'expression conjuguée de $7+3\sqrt{5}$ ; c'est à dire $7-3\sqrt{5}.$
On obtient alors :
$\begin{array}{rcl} x&=&\dfrac{4}{7+3\sqrt{5}}\\ \\&=&\dfrac{4\times(7-3\sqrt{5})}{(7+3\sqrt{5})(7-3\sqrt{5})}\\ \\&=&\dfrac{4\times(7-3\sqrt{5})}{(7)^{2}-(3\sqrt{5})^{2}}\\ \\&=&\dfrac{4\times(7-3\sqrt{5})}{49-9\times 5}\\ \\&=&\dfrac{4\times(7-3\sqrt{5})}{49-45}\\ \\&=&\dfrac{4\times(7-3\sqrt{5})}{4}\\ \\&=&7-3\sqrt{5}\end{array}$
D'où, $\boxed{x=7-3\sqrt{5}}$
b) Justifions que $y$ est négatif.
Soit : $y=3\sqrt{5}-7$ alors, $y$ est négatif si, et seulement si, $3\sqrt{5}-7<0$ ; c'est à dire $3\sqrt{5}<7.$
Ce qui revient donc à comparer $3\sqrt{5}\ $ et $\ 7.$
Comme ces deux nombres sont tous positifs alors, les comparer revient tout simplement à comparer leur carré.
On a : $(3\sqrt{5})^{2}=9\times 5=45\ $ et $\ (7)^{2}=49$
Or, $\ 49>45$ donc, $7$ est supérieur à $3\sqrt{5}$
Par suite, $3\sqrt{5}-7<0.$ D'où, $y<0$
c) Justifions que $x=-y$
D'après la question a), on a :
$\begin{array}{rcl} x&=&7-3\sqrt{5}\\ \\&=&-3\sqrt{5}+7\\ \\&=&-(3\sqrt{5}-7)\\ \\&=&-y\end{array}$
Ainsi, $\boxed{x=-y}$
d) Encadrons $x$ à $10^{-2}$ près.
Soit : $x=7-3\sqrt{5}$ avec $2.236<\sqrt{5}<2.237$ alors, on a :
$\begin{array}{rcrcccl} 2.236<\sqrt{5}<2.237&\Rightarrow&-2.237&<&-\sqrt{5}&<&-2.236\\ \\&\Rightarrow&3\times(-2.237)&<&3\times(-\sqrt{5})&<&3\times(-2.236)\\ \\&\Rightarrow&-6.711&<&-3\sqrt{5}&<&-6.708\\ \\&\Rightarrow&7-6.711&<&7-3\sqrt{5}&<&7-6.708\\ \\&\Rightarrow&0.289&<&7-3\sqrt{5}&<&0.292\\ \\&\Rightarrow&0.28&<&7-3\sqrt{5}&<&0.29\end{array}$
Par suite, $\boxed{0.28<x<0.29}$
e) On pose : $z=(x-y)^{2}$
Justifions que $\sqrt{z}=-2y$
On a :
$\begin{array}{rcl}\sqrt{z}&=&\sqrt{(x-y)^{2}}\\ \\&=&|x-y|\end{array}$
Or, d'après la question c), $x=-y$ donc,
$\begin{array}{rcl}\sqrt{z}&=&|x-y|\\ \\&=&|-y-y|\\ \\&=&|-2y|\\ \\&=&|-2|\times|y|\\ \\&=&2\times|y|\end{array}$
Comme d'après la question b), $y$ est négatif alors, $|y|=-y$
Par suite, $\sqrt{z}=2\times(-y)=-2\times y$
D'où, $\boxed{\sqrt{z}=-2y}$
Exercice 2
"Le Sénégal vient d'administrer une belle leçon de démocratie à la face du monde par l'organisation d'élection présidentielle incontestée. Le vaincu reconnait sa défaite, félicite le vainqueur".
Une étude statistique portant sur les $30$ mots de ce texte (un mot quelconque est considéré autant de fois qu'il apparait dans le texte), a donné le diagramme circulaire ci-dessous :
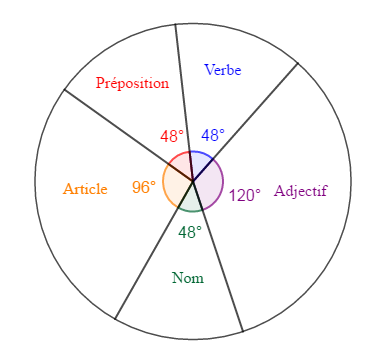
1) Le caractère étudié est la Nature grammaticale des mots.
2) Ce caractère est de nature qualitative.
3) Les modalités de ce caractère sont :
$-\ $ Nom
$-\ $ Adjectif
$-\ $ Verbe
$-\ $ Préposition
$-\ $ Article
4) Dressons le tableau des effectifs de cette série.
Soit $n$ l'effectif partiel d'une modalité occupant un angle égal à $\alpha^{\circ}$ dans le diagramme circulaire ci-dessus.
Soit $N$ l'effectif total égal au nombre total de mots donc, $N=30.$
Alors, on a :
$$\alpha^{\circ}=\dfrac{360^{\circ}\times n}{N}\ \Rightarrow\ n=\dfrac{\alpha^{\circ}\times N}{360^{\circ}}$$
D'où, le le tableau des effectifs suivant :
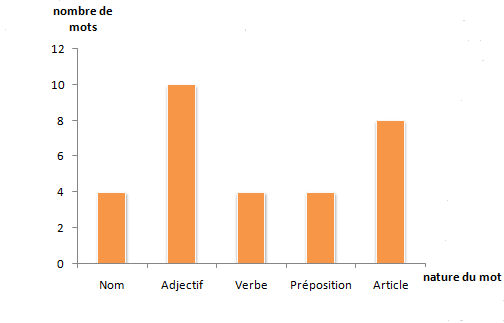
$$\begin{array}{|l|c|c|c|c|c|}\hline\text{Modalités}&\text{Nom}&\text{Adjectif}&\text{Verbe}&\text{Préposition}&\text{Article}\\ \hline\text{Effectifs}&4&10&4&4&8\\ \hline\end{array}$$
5) Construisons le diagramme à bandes de cette série.
Exercice 3
1) Construisons un triangle $MON$ rectangle en $N$ tel que :
$$MN=7.5\;cm\ \text{ et }\ \widehat{MON}=30^{\circ}$$
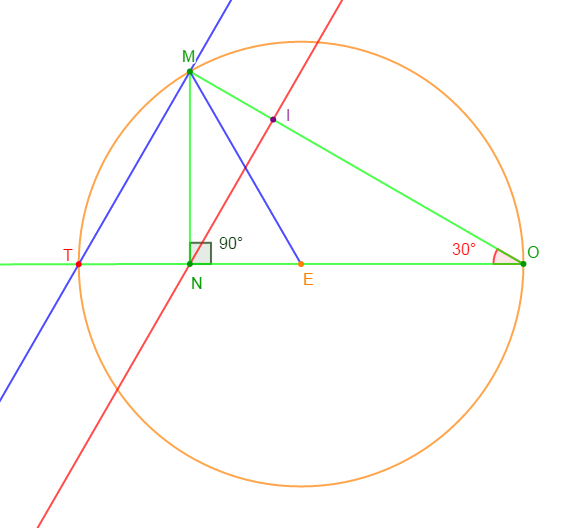
2) Calculons $MO$
$MON$ étant un triangle rectangle en $N$ alors, $\sin\widehat{MON}=\dfrac{MN}{MO}$
Or, $\sin\widehat{MON}=\sin 30^{\circ}=\dfrac{1}{2}$ donc,
$\begin{array}{rcrcl}\dfrac{MN}{MO}=\dfrac{1}{2}&\Rightarrow&1\times MO&=&2\times MN\\ \\&\Rightarrow&MO&=&2\times 7.5\\ \\&\Rightarrow&MO&=&15\end{array}$
D'où, $\boxed{MO=15\;cm}$
Calculons $NO$
De la même manière, on a : $\cos\widehat{MON}=\dfrac{NO}{MO}$
Comme $\cos\widehat{MON}=\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$ alors,
$\begin{array}{rcrcl}\dfrac{NO}{MO}=\dfrac{\sqrt{3}}{2}&\Rightarrow&NO&=&\dfrac{\sqrt{3}}{2}\times MO\\ \\&\Rightarrow&NO&=&\dfrac{\sqrt{3}}{2}\times 15\\ \\&\Rightarrow&NO&=&\dfrac{15\sqrt{3}}{2}\end{array}$
Ainsi, $\boxed{NO=\dfrac{15\sqrt{3}}{2}\;cm}$
3) Soit $I$ le pied de la hauteur issue de $N.$
Calculons $NI$
Comme $MON$ est un triangle rectangle en $N\ $ et $\ I$ le pied de la hauteur issue de $N$ alors, on a :
$$NI=\dfrac{MN\times NO}{MO}$$
Par suite,
$\begin{array}{rcl} NI=\dfrac{MN\times NO}{MO}&=&\dfrac{7.5\times \dfrac{15\sqrt{3}}{2}}{15}\\ \\&=&\dfrac{\dfrac{7.5\times 15\sqrt{3}}{2}}{15}\\ \\&=&\dfrac{7.5\times 15\sqrt{3}}{2\times 15}\\ \\&=&\dfrac{7.5\sqrt{3}}{2}\end{array}$
D'où, $\boxed{NI=\dfrac{7.5\sqrt{3}}{2}\;cm}$
4) La droite passant par $M$ et parallèle à la droite $(NI)$ coupe la droite $(ON)\ $ en $\ T.$
Calculons $MT$
Comme les droites $(MO)\ $ et $\ (ON)$ sécantes en $O$ sont coupées par deux droites parallèles $(NI)\ $ et $\ (MT)$ alors, les triangles $ONI\ $ et $\ OMT$ sont en position de Thalès.
Donc, en appliquant le théorème de Thalès, on obtient : $$\dfrac{ON}{OT}=\dfrac{OI}{OM}=\dfrac{NI}{MT}$$
Ainsi,
$\begin{array}{rcrcl}\dfrac{OI}{OM}=\dfrac{NI}{MT}&\Rightarrow&OI\times MT&=&OM\times NI\\ \\&\Rightarrow&MT&=&\dfrac{OM\times NI}{OI}\end{array}$
Par suite, $\boxed{MT=\dfrac{OM\times NI}{OI}}$
Calculons $OI$
En utilisant les relations métriques dans le triangle rectangle $MNO$, on obtient :
$$NO^{2}=OI\times MO$$
Ainsi, $OI=\dfrac{NO^{2}}{MO}$
Par suite,
$\begin{array}{rcl} OI&=&\dfrac{\left(\dfrac{15\sqrt{3}}{2}\right)^{2}}{15}\\ \\&=&\dfrac{15^{2}\times 3}{4\times 15}\\ \\&=&\dfrac{15\times 3}{4}\\ \\&=&\dfrac{45}{4}\\ \\&=&11.25\end{array}$
D'où, $\boxed{OI=11.25\;cm}$
Autre méthode
$NIO$ étant un triangle rectangle en $I$ alors, $\dfrac{OI}{NO}=\cos\widehat{ION}$
Or, $\cos\widehat{ION}=\cos 30^{\circ}=\dfrac{\sqrt{3}}{2}$
Par suite,
$\begin{array}{rcrcl}\dfrac{OI}{NO}=\dfrac{\sqrt{3}}{2}&\Rightarrow&OI&=&NO\times\dfrac{\sqrt{3}}{2}\\ \\&\Rightarrow&OI&=&\dfrac{15\sqrt{3}}{2}\times\dfrac{\sqrt{3}}{2}\\ \\&\Rightarrow&OI&=&\dfrac{15\times 3}{4}\\ \\&\Rightarrow&OI&=&\dfrac{45}{4}\\ \\&\Rightarrow&OI&=&11.25\end{array}$
Ainsi, $\boxed{OI=11.25\;cm}$
En reportant cette valeur de $OI$ dans l'expression de $MT$, on obtient :
$\begin{array}{rcl} MT=\dfrac{OM\times NI}{OI}&=&\dfrac{15\times\dfrac{7.5\sqrt{3}}{2}}{11.25}\\ \\&=&\dfrac{15\times 7.5\sqrt{3}}{11.5\times 2}\\ \\&=&\dfrac{112.5\sqrt{3}}{22.5}\\ \\&=&5\sqrt{3}\end{array}$
D'où, $\boxed{MT=5\sqrt{3}\;cm}$
5) Soit $E$ le centre du cercle circonscrit au triangle $MOT.$
Démontrons que $MET$ est un triangle équilatéral.
Pour cela, il suffit de montrer que $MT=ME=ET.$
On sait que $MOT$ est un triangle rectangle en $M.$
En effet, $(MT)//(NI)\ $ et $\ (NI)$ perpendiculaire à $(MO)$ donc, $(MT)$ aussi est perpendiculaire à $(MO).$
D'où, $MOT$ est un triangle rectangle en $M.$
Par suite, le centre $E$ du cercle circonscrit au triangle $MOT$ sera le milieu du segment $[OT].$
$M\ $ et $\ T$ appartiennent au cercle circonscrit donc, $\boxed{ET=ME}$
Calculons $ET$
On a : $ET=\dfrac{OT}{2}\ \Rightarrow\ OT=2ET$
Dans le triangle rectangle $MOT$, on a : $\dfrac{MT}{OT}=\sin 30^{\circ}.$
Or, $\sin 30^{\circ}=\dfrac{1}{2}$ donc, $\dfrac{MT}{OT}=\dfrac{1}{2}\ \Rightarrow\ OT=2MT$
Par suite,
$\begin{array}{rcrcl}\left.\begin{array}{rcl} OT&=&2ET\\OT&=&2MT\end{array}\right\rbrace&\Rightarrow&2ET&=&2MT\\ \\&\Rightarrow&ET&=&MT\end{array}$
Ainsi, $\boxed{ET=ME=MT=5\sqrt{3}\;cm}$
D'où, le triangle $MET$ est équilatéral.
Exercice 4
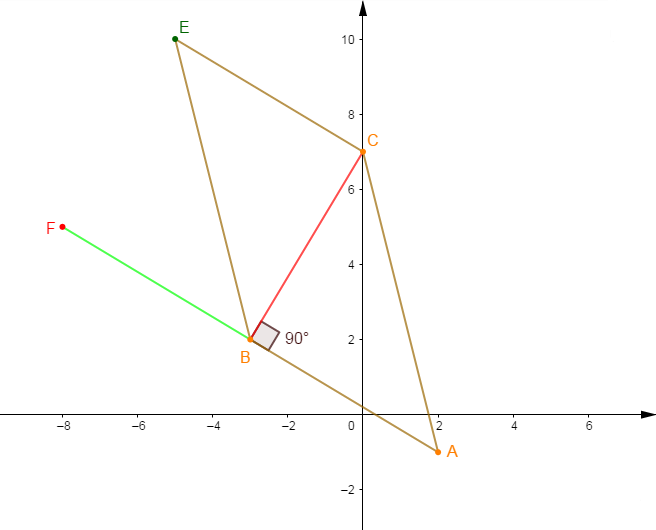
Dans le plan muni d'un repère orthonormal $(O\;,\ \vec{i}\;,\ \vec{j})$ on donne les points :
$$A\begin{pmatrix} 2\\-1\end{pmatrix}\;,\ B\begin{pmatrix} -3\\2\end{pmatrix}\ \text{ et }\ C\begin{pmatrix} 0\\7\end{pmatrix}$$

1) Démontrons que $\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}$ sont orthogonaux.
Calculons d'abord les coordonnées de $\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}$
On a :
$\overrightarrow{AB}\begin{pmatrix} -3-2\\2-(-1)\end{pmatrix}=\begin{pmatrix} -5\\3\end{pmatrix}$
$\overrightarrow{BC}\begin{pmatrix} 0-(-3)\\7-2\end{pmatrix}=\begin{pmatrix} 3\\5\end{pmatrix}$
Donc,
$$\overrightarrow{AB}\begin{pmatrix} -5\\3\end{pmatrix}\quad\text{et}\quad\overrightarrow{BC}\begin{pmatrix} 3\\5\end{pmatrix}$$
Montrons que les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}$ sont orthogonaux.
On a :
$\begin{array}{rcl} x_{\overrightarrow{AB}}\times x_{\overrightarrow{BC}}+y_{\overrightarrow{AB}}\times y_{\overrightarrow{BC}}&=&(-5)\times 3+3\times 5\\ \\&=&-15+15\\ \\&=&0\end{array}$
Donc, les coordonnées des vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}$ vérifient la propriété :
$$x_{\overrightarrow{AB}}\times x_{\overrightarrow{BC}}+y_{\overrightarrow{AB}}\times y_{\overrightarrow{BC}}=0$$
Par suite, les vecteurs $\overrightarrow{AB}\ $ et $\ \overrightarrow{BC}$ sont orthogonaux.
2) Calculons les coordonnées du point $E$ tel que $ABEC$ soit un parallélogramme.
$ABEC$ un parallélogramme alors, $\overrightarrow{AB}=\overrightarrow{CE}$
Or, $\overrightarrow{CE}\begin{pmatrix} x_{E}-0\\y_{E}-7\end{pmatrix}=\begin{pmatrix} x_{E}\\y_{E}-7\end{pmatrix}\ $ et $\ \overrightarrow{AB}=\begin{pmatrix} -5\\3\end{pmatrix}$
Donc,
$\begin{array}{rcrcl}\overrightarrow{AB}=\overrightarrow{CE}&\Leftrightarrow&\begin{pmatrix} -5\\3\end{pmatrix}&=&\begin{pmatrix} x_{E}\\y_{E}-7\end{pmatrix}\\ \\&\Leftrightarrow&\begin{pmatrix} -5\\3+7\end{pmatrix}&=&\begin{pmatrix} x_{E}\\y_{E}\end{pmatrix}\\ \\&\Leftrightarrow&\begin{pmatrix} -5\\10\end{pmatrix}&=&\begin{pmatrix} x_{E}\\y_{E}\end{pmatrix}\end{array}$
Ainsi, $x_{E}=-5\ $ et $\ y_{E}=10$
D'où,
$$E\begin{pmatrix} -5\\10\end{pmatrix}$$
3) Soit $F$ l'image de $B$ par la translation de vecteur $\overrightarrow{CE}.$
Calculons les coordonnées de $F$
On a : $F=t_{\overrightarrow{CE}}(B)$ donc, $\overrightarrow{BF}=\overrightarrow{CE}$
Soit $\overrightarrow{CE}=\begin{pmatrix} -5\\3\end{pmatrix}\ $ et $\ \overrightarrow{BF}\begin{pmatrix} x_{F}-(-3)\\y_{F}-2\end{pmatrix}=\begin{pmatrix} x_{F}+3\\y_{E}-2\end{pmatrix}$ alors, on a :
$\begin{array}{rcl}\overrightarrow{BF}=\overrightarrow{CE}&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{F}+3&=&-5\\ \\y_{F}-2&=&3\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{F}&=&-5-3\\ \\y_{F}&=&3+2\end{array}\right.\\ \\&\Leftrightarrow&\left\lbrace\begin{array}{rcl} x_{F}&=&-8\\ \\y_{F}&=&5\end{array}\right.\end{array}$
Ainsi,
$$F\begin{pmatrix} -8\\5\end{pmatrix}$$
4) Justifions que $B$ est le milieu de $\left[AF\right]$
$ABEC$ étant un parallélogramme alors, $\overrightarrow{AB}=\overrightarrow{CE}$
Or, d'après la question 3) $\overrightarrow{BF}=\overrightarrow{CE}$
Donc, $\overrightarrow{AB}=\overrightarrow{CE}=\overrightarrow{BF}$
Par suite, $\overrightarrow{AB}=\overrightarrow{BF}$
D'où, $B$ est milieu de $[AF]$
Autre méthode
On a :
$\begin{pmatrix}\dfrac{x_{F}+x_{A}}{2}\\ \\\dfrac{y_{F}+y_{A}}{2}\end{pmatrix}=\begin{pmatrix}\dfrac{-8+2}{2}\\ \\\dfrac{5-1}{2}\end{pmatrix}=\begin{pmatrix}\dfrac{-6}{2}\\ \\\dfrac{4}{2}\end{pmatrix}=\begin{pmatrix} -3\\2\end{pmatrix}$
Or, $B$ est de coordonnées $\begin{pmatrix} -3\\2\end{pmatrix}$
Donc, les coordonnées de $B$ vérifient :
$$x_{B}=\dfrac{x_{F}+x_{A}}{2}\quad\text{et}\quad y_{B}=\dfrac{y_{F}+y_{A}}{2}$$
D'où, $B$ est le milieu de $[AF]$
Auteur:
Diny Faye

Commentaires
Anonyme (non vérifié)
mer, 09/02/2020 - 18:22
Permalien
Bon boulot ! ! ! !
Sasa (non vérifié)
lun, 08/02/2021 - 18:57
Permalien
Vraiment merci beaucoup vous
Ajouter un commentaire