Oscillations électriques libres et oscillations électriques forcées - Ts2

 

La bobine et le condensateur étant capables de stocker puis de redonner de l'énergie, nous nous intéresserons aux échanges énergétiques entre les différents composants d'un tel dipôle qui peut se comporter comme un oscillateur électrique.

$\ast\ $L'interrupteur $K_{1}$ est fermé, $K_{2}$ est ouvert

 

 

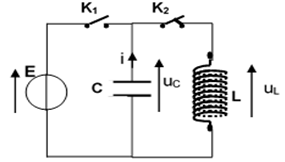
On considère le circuit électrique schématisé ci-dessous, lorsque le condensateur se charge complètement, sa charge est maximale $Q_{\text{max}}.$

 

D'après la loi des tensions : \begin{eqnarray} u_{C} &=& u_{G}\nonumber\\\Rightarrow\dfrac{Q_{\text{max}}}{C}&=&E\nonumber\\\Rightarrow Q_{\text{max}}&=& CE \end{eqnarray} 

 

L'énergie électrique emmagasinée par le condensateur est 

$$E_{e}=\dfrac{1}{2}\dfrac{Q_{\text{max}}^{2}}{C}=\dfrac{1}{2}CE^{2}$$

  

$\ast\ $L'interrupteur $K_{1}$ est ouvert, $K_{2}$ est fermé

 

Le condensateur se décharge dans une bobine pure, on obtient des oscillations électriques libres non amorties (oscillations sinusoïdales). L'oscillogramme ci-dessous représente les variations de la tension $u^{c}$ aux bornes du condensateur 

 

 

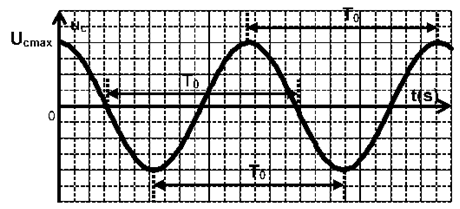
$T_{0}$ est la période propre du circuit $LC$

En ouvrant l'interrupteur $K_{1}$ et en fermant l'interrupteur $K_{2}$ le condensateur se décharge à travers la bobine pure.

 

La loi d'additivité des tensions s'écrit :