I. Introduction
Étymologiquement, une conique est une courbe plane obtenue en coupant un cône de révolution par un plan.
Les coniques propres obtenues ainsi sont les cercles, les ellipses, les paraboles, les hyperboles, mais dans certains cas, l'intersection d'un cône et d'un plan donne un point, une droite ou deux droites, ce sont des coniques impropres ou dégénérées.
Plusieurs définitions des coniques sont possibles (foyers et directrices, définition bifocale,...), la seule qui englobe tous les cas particuliers est la définition analytique suivante : une conique est une courbe plane définie par une équation qui peut s'écrire sous la forme $$ax^{2}+2bxy+cy^{2}+2dx+2ey+f=0$$
II. Définitions par foyer, directrice et excentricité
1. Définitions
$\centerdot\ \ $ Soit $F$ un point du plan, $e$ un réel > 0, et $D$ une droite ne contenant pas $F$, on appelle conique de foyer $F$, d'excentricité $e$, et de directrice $D$, l'ensemble $\Gamma$ des points $M$ du plan tels que :
$MF=e\times d(M,\ D)$ où $d(M,\ D)$ est la distance de $M$ à la droite $D$.
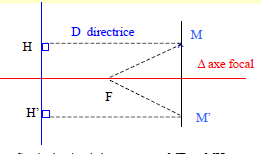
On peut aussi donner la définition ainsi : $M\in \Gamma \Leftrightarrow MF=eMH$ où $H$ est le projeté orthogonal de $M$ sur $D$
Si $0<e<1\;$, la conique $\Gamma$ est une ellipse
Si $e=1\;$, la conique $\Gamma$ est une parabole
Si $e>1\;$, la conique $\Gamma$ est une hyperbole
Sur le dessin ci-dessus, on a $MF=eMH$ avec $e$ tel que $0<e<1\ $ ($e$ de l'ordre de $0.6$)
$\centerdot\ \ $ On appelle axe focal de la conique la droite perpendiculaire à $D$ et passant par $F$.
$\centerdot\ \ $ L'axe focal d'une conique est un axe de symétrie pour la conique.
$\centerdot\ \ $ Un sommet de la conique est un point d'intersection entre la conique et son axe focal.
Quatre coniques ayant même foyer et même directrice.
Parabole $(e=1)\ $ : $\ MF=MH$ et $NF=NH'$
2.Sommets sur l'axe focal
Une conique $\mathbf{C}$ étant donnée par un foyer $F$, son excentricité $e$ et une directrice $D$, cherchons les points de l'axe focal qui appartiennent à la conique. Soit $K$ est le projeté orthogonal de $F$ sur $D$.
Les points $M$ cherchés doivent vérifier $MF=e\times d(M,\ D)$, soit ici $MF=eMK$, les points $M$, $\ F$, $\ K$ étant alignés.
$\centerdot\ \ $ Si $e=1\;;$ $\ MF=MK$ entraîne que le seul point de la conique sur l'axe focal
est le milieu $S$ de $[FK]$ (sommet de $C$).
$\centerdot\ \ $ Sinon $MF=eMK\;$, les points $M$, $\ F$, $\ K$ étant alignés, cela entraîne que
$\overrightarrow{MF}=e\overrightarrow{MK}\ $ ou $\ \overrightarrow{MF}=-e\overrightarrow{MK}$
Il y a donc deux points appelés sommets qui appartiennent à la conique et qui sont sur l'axe focal :
$S$ tel que $\overrightarrow{SF}=-e\overrightarrow{SK}$ soit $\overrightarrow{SF}+e\overrightarrow{SK}=\overrightarrow{0}$, $\ S$ est le barycentre de $(F,\ 1)$;
$\ (K,\ e)$, on a donc $\overrightarrow{FS}=\dfrac{e}{1+e}\overrightarrow{FK}$
et $S'$ tel que $\overrightarrow{S'F}=e\vec{S'K}$ soit $\overrightarrow{S'F}-e\vec{S'K}=\vec{0}$, $\ S'$ est le barycentre de
$(F,\ 1)$; $\ (K,\ -e)$, on a donc $\overrightarrow{FS'}=\dfrac{-e}{1-e}\overrightarrow{FK}$
III. Equation réduite et forme des coniques : première approche
1. Paraboles
Soit $F$ un point du plan, $e$ un réel >0, et $D$ une droite ne contenant pas $F$.
On considère la parabole $\mathcal{P}$ de foyer $F$, d'excentricité $e=1$, et de directrice $D$.
C'est l'ensemble des points $M$ du plan $P$ tels que $MF=d(M\;,\ D)$ ou encore $M\in P \Leftrightarrow MF=MH$ où $H$ est le projeté orthogonal de $M$ sur $D.$
Soit $K$ le projeté orthogonal de $F$ sur $D$.
Considérons un repère orthonormé $(O\;;\ \vec{i}\;,\ \vec{j})$ où $O$ est le milieu de $[FK]$ et
$\vec{i}=\dfrac{1}{OF}\overrightarrow{OF}$.
Notons $p=KF$, $p$ est appelé le paramètre de la parabole.
Alors, dans ce repère, de l'égalité définissant la parabole $MF=d(M,\ D)$, on déduit une équation réduite de la parabole $$y^{2}=2px$$
2. Ellipses
Soit $F$ un point du plan, $e$ un réel de $]0; 1[$, et $D$ une droite ne contenant pas $F$.
On considère l'ellipse $\mathcal{E}$ de foyer $F$, d'excentricité $e$ et de directrice $D$.
C'est l'ensemble des points $M$ du plan $P$ tels que $MF=e\times d(M,\ D)$ ou encore $M\in\mathcal{E} \Leftrightarrow MF=eMH$ où $H$ est le projeté orthogonal de $M$ sur $D$
$\mathcal{E}$ admet deux sommets $S$ et $S'$ (cf.II2) où $S$ est le barycentre de $(F,\ 1)$; $\ (K,\ e)$ et $S'$ est le barycentre de $(F,\ 1)$; $\ (K,\ -e)$.
Considérons un repère orthonormal $(O\;,\ \vec{i}\;,\ \vec{j})$ tel que $O$
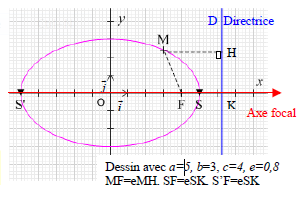
est le milieu de $[SS']$ et avec $K$ projeté orthogonal de $F$ sur $D$
, $\vec{i}=\dfrac{1}{OS}\overrightarrow{OS}$.
Notons $a=OS$, $\ c=OF$ et $b=\sqrt{a^{2}-c^{2}}$
Alors, dans ce repère, de l'égalité définissant l'ellipse $MF=e\times d(M\;,\ D)$, on déduit
une équation réduite de l'ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$
$\centerdot\ \ $ L'équation réduite étant invariante par transformation de $x$ en $-x$ et de $y$ en $-y$, on en déduit que les ellipse admettent deux axes de symétrie $(Ox)$ et $(Oy)$ et donc un centre de symétrie $O$.
$\centerdot\ \ $ De $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$, on déduit $y^{2}=b^{2}\sqrt{1-\dfrac{x^{2}}{a^{2}}}$ et donc que l'ellipse $\varepsilon$ est la réunion des courbes des fonctions $x \rightarrow \dfrac{b}{a}\sqrt{a^{2}-x^{2}}$ et $x \rightarrow -\dfrac{b}{a}\sqrt{a^{2}-x^{2}}$
Ces deux courbes sont symétriques par rapport à $(Ox)$, et les fonctions sont toutes deux définies sur $[-a;\ a]$
3. Hyperboles
Soit $F$ un point du plan, $e$ un réel $e>1$ et $D$ une droite ne contenant pas $F$.
On considère l'hyperbole $\mathcal{H}$ de foyer $F$, d'excentricité $e$, et de directrice $D$.
C'est l'ensemble des points $M$ du plan $P$ tels que $MF=e\times d(M,\ D)$ ou encore $M\in H \Longleftrightarrow MF=eMH$ où $H$ est le projeté orthogonal de $M$ sur $D$.
$\mathcal{H}$ admet deux sommets $S$ et $S'$ (cf.II2) où $S$ est le barycentre de $(F,\ 1)$; $\ (K, e)$, et $S'$ est le barycentre de $(F,\ 1)$; $\ (K,\ -e)$.
Considérons un repère orthonormal $(O;\ \vec{i},\ \vec{j})$ tel que $O$
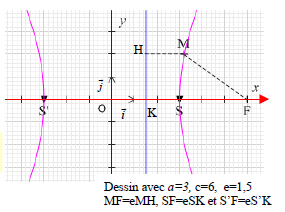
est le milieu de $[SS']$ et avec $K$ projeté orthogonal de $F$ sur $D$.
$\vec{i}=\dfrac{1}{OS}\overrightarrow{OS}$.
Notons $a=OS$, $\ c=OF$ et $b=\sqrt{c^{2}-a^{2}}$
Alors, dans ce repère, de l'égalité définissant l'hyperbole $MF=e\times d(M,\ D)$, on déduit
une équation réduite de l'hyperbole $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$
$\centerdot\ \ $ L'équation réduite étant invariante par transformation de $x$ en $-x$ et de $y$ en $-y$, on en déduit que les ellipse admettent deux axes de symétrie $(Ox)$ et $(Oy)$ et donc un centre de symétrie $O$.
$\centerdot\ \ $ De $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$, on déduit $y^{2}=b^{2}\sqrt{\dfrac{x^{2}}{a^{2}}-1}$ et donc que l'hyperbole $\mathcal{H}$ est la réunion des courbes des fonctions $x \rightarrow \dfrac{b}{a}\sqrt{x^{2}-a^{2}}$ et $x \rightarrow -\dfrac{b}{a}\sqrt{x^{2}-a^{2}}$
Ces deux courbes sont symétriques par rapport à $(Ox)$, et les fonctions sont toutes deux définies sur $]-\infty;\ -a]\cup[a;\ +\infty[$
IV. Paraboles, Ellipses et Hyperboles
1. Paraboles
Soit $p$ un réel non nul.
1.1. Courbes
$\centerdot\ \ $ Paraboles d'axes $(Ox)$
Dans un repère orthonormé $(O;\ \vec{i},\ \vec{j})$ la courbe d'équation $y^{2}=2px$ est la parabole de foyer $F\left(\dfrac{p}{2},\ 0\right)$ et de directrice d'équation $x=-\dfrac{p}{2}$. $\ |p|$ est le paramètre de la parabole, $O$ est le sommet de la parabole.
La parabole d'équation $y^{2}=2px$ est la réunion des courbes des fonctions $x \rightarrow \sqrt{2px}$ et $x \rightarrow -\sqrt{2px}$ symétriques par rapport à $(Ox)$
$\centerdot\ \ $ Paraboles d'axes $(Oy)$
Dans un repère orthonormé $(O;\ \vec{i},\ \vec{j})$ la courbe d'équation $x^{2}=2py$ est la parabole de foyer $F\left(0,\ \dfrac{p}{2}\right)$ et de directrice d'équation $y=-\dfrac{p}{2}$. $\ |p|$ est le paramètre de la parabole, $O$ est le sommet de la parabole.
1.2. Remarques
Quelques éléments pour retrouver rapidement la forme des paraboles à partir d'une équation :
$\centerdot\ \ $ Pour une équation $x^{2}=2py$, ou $y=\dfrac{1}{2p}x^{2}$ du type $y=kx^{2}$, la parabole a $(Oy)$ comme axe de symétrie comme la courbe d'équation $y=x^{2}$
De plus $x^{2}=2py \Longrightarrow y=\dfrac{1}{2p}x^{2}$ donc $\left\{
\begin{array}{rl}
\text{si}& p>0 & \text{pour tout }\ x,&y >0\\
\text{si} &p<0 & \text{pour tout }\ x,&y<0
\end{array}
\right.$
$\centerdot\ \ $ Pour une équation $y^{2}=2px$, la parabole est la réunion des courbes des fonctions $x \rightarrow \sqrt{2px}$ et $x \rightarrow -\sqrt{2px}$.
Ces deux courbes sont symétriques par rapport à $(Ox)$, et les fonctions sont toutes deux définies sur $[0,\ +\infty[$ si $p>0$ et définies sur $]-\infty,\ 0]$ si $p<0$.
1.3. Tangentes
$\centerdot\ \ $ Equation et "règle du dédoublement" :
Pour une parabole d'équation : $y^{2}=2px$ : une équation de la tangente en $M_{0}$ est : $yy_{0}=p(x+x_{0})$
Pour une parabole d'équation : $x^{2}=2py$ : une équation de la tangente en $M_{0}$ est : $xx_{0}=p(y+y_{0})$
Démonstration en exercice, ces équations se retrouvent très facilement en utilisant la "règle du dédoublement"
En passant de l'équation de la courbe à l'équation de la tangente, $x^{2} \rightarrow xx_{0}$, $\ y^{2} \rightarrow yy_{0}$, $\ 2x \rightarrow (x+x_{0})$ et $2y \rightarrow (y+y_{0})$
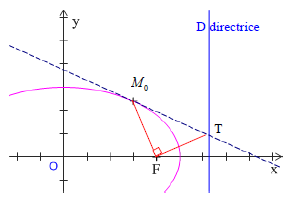
$\centerdot\ \ $ Propriété géométrique
$T$ étant le point d'intersection de la tangente en $M_{0}$ avec la directrice $D$
La tangente $(M_{0}T)$ est la médiatrice de $[FH]$, et le triangle $M_{0}FT$ est un triangle rectangle en $F$.
2. Ellipses
2.1. Courbes
Soient $a>0$ et $b>0$
Dans un repère orthonormé $(O\;,\ \vec{i}\;,\ \vec{j})$, soit $\mathcal{E}$ la courbe d'équation $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$
$-\ $ si $a=b\;$, $\ \mathcal{E}$ est un cercle
$-\ $ si $a\neq b\;$, $\ \mathcal{E}$ est une ellipse de sommets $A(a,\ 0)$, $\ A'(-a,\ 0)$, $\ B(0,\ b)$ et $B'(0,\ -b)$, de centre $O$
Toute ellipse admet exactement deux foyers directrices associées.
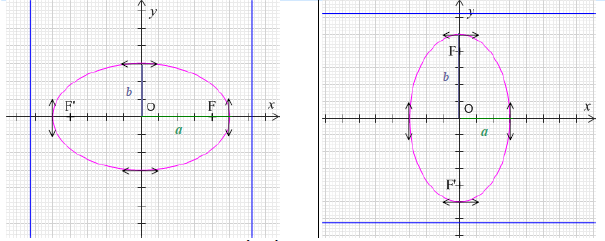
$$\begin{array}{rcl}\text{Ellipse }\ \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1\ \text{ avec }\ a>b& &\text{Ellipse }\ \dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1\ \text{ avec }\ a<b \\ \text{Axe focal }\ (Ox)& &\text{Axe focal }\ (Oy) \\ \text{Avec }\ c=\sqrt{a^{2}-b^{2}}& &\text{Avec }\ c=\sqrt{b^{2}-a^{2}} \\ \text{foyers }\ F(c\;,\ 0)\ \text{ et }\ F'(-c\;,\ 0)& &\text{foyers }\ F(0\;,\ c)\ \text{ et }\ F'(0\;,\ -c) \\ \text{Directrices }\ x=\pm\dfrac{a^{2}}{c}& &\text{Directrices }\ x=\pm\dfrac{b^{2}}{c} \\ \text{excentricité }\ e=\dfrac{c}{a}& &\text{excentricité }\ e=\dfrac{c}{b}\end{array}$$
Remarque :
Pour une ellipse $\mathcal{E}$ d'équation $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ avec $a>b$, $a$ est souvent appelé le "demi grand axe" et $b$ le "demi petit axe" (grand axe = $2a$ et petit axe = $2b$). Dans le cas où $a<b$, c'est $b$ qui est appelé le "demi grand axe" et $a$ le "demi petit axe".
2.2. Tangentes
$\centerdot\ \ $ Pour une ellipse d'équation $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ :
une équation de la tangente en $M_{0}$ est $\dfrac{xx_{0}}{a^{2}}+\dfrac{yy_{0}}{b^{2}}=1$
Démonstration en exercice, cela se retrouve très facilement en utilisant la "règle du dédoublement"
On passe de l'équation de la courbe à l'équation de la tangente $x^{2} \rightarrow xx_{0}$, $y^{2} \rightarrow yy_{0}$
$\centerdot\ \ $ Propriété géométrique
$T$ étant le point d'intersection de la tangente en $M_{0}$ avec la directrice $D$, le triangle $M_{0}FT$ est un triangle rectangle en $F$
3. Hyperboles
3.1. Courbes
Soient $a>0$ et $b>0$
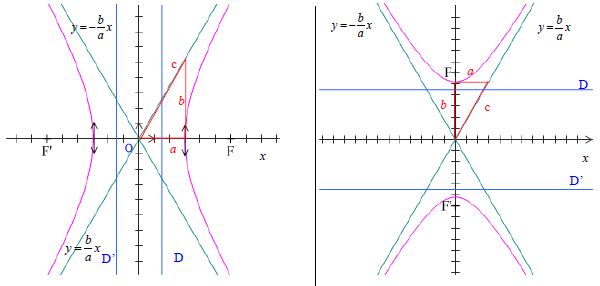
Dans un repère orthonormé $(O\;;\ \vec{i}\;,\ \vec{j})$, les courbes $H_{1}$ et $H_{2}$ d'équations respectives $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ et $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=-1$ sont des hyperboles de $O$, d'axes $(Ox)$ et $(Oy)$
Toute hyperbole admet exactement deux foyers et deux directrices associées.
$$\begin{array}{rcl}\text{Hyperbole }\ \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1& &\text{Hyperbole }\ \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=-1 \\ \text{Axe focal }\ (Ox)& &\text{Axe focal }\ (Oy) \\ \text{asymptotes }\ y=\pm \dfrac{b}{a}x& &\text{asymptotes }\ y=\pm \dfrac{b}{a}x \\ \text{Avec }\ c=\sqrt{a^{2}+b^{2}}& &\text{Avec }\ c=\sqrt{b^{2}+a^{2}} \\ \text{foyers }\ F(c\;,\ 0)\ \text{ et }\ F'(-c\;,\ 0)& &\text{foyers }\ F(0\;,\ c)\ \text{ et }\ F'(0\;,\ -c) \\ \text{Directrices }\ D\;,\ D'\ :\ x=\pm\dfrac{a^{2}}{c}& &\text{Directrices }\ D\;,\ D'\ :\ x=\pm\dfrac{b^{2}}{c} \\ \text{excentricité }\ e=\dfrac{c}{a}& &\text{excentricité }\ e=\dfrac{c}{b}\end{array}$$
$-\ $ Si $a=b$, l'hyperbole est dite équilatère
Propriété :
Dans le repère ayant pour axes les asymptotes $\Delta$ et $\Delta'$, l'équation de l'hyperbole est de la forme $xy=k$
$\left(\text{ on retrouve les fonctions } x \rightarrow \dfrac{k}{x}\right)$
3.2. Tangentes
$\centerdot\ \ $ Equation et "règle du dédoublement" :
Pour une hyperbole d'équation : $\ \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1\ $ : une équation de la tangente en $M_{0}$ est : $\ \dfrac{xx_{0}}{a^{2}}-\dfrac{yy_{0}}{b^{2}}=1$
Pour les hyperboles d'équation ; $\ \dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=-1\ $ : une équation de la tangente en $M_{0}$ est : $\ \dfrac{xx_{0}}{a^{2}}-\dfrac{yy_{0}}{b^{2}}=-1$
Démonstration en exercice. Ces équations se retrouvent très facilement en utilisant la "règle du dédoublement"
On passe de l'équation de la courbe à l'équation de la tangente, $x^{2} \rightarrow xx_{0}$, $y^{2} \rightarrow yy_{0}$
$\centerdot\ \ $ Propriété géométrique
$T$ étant le point d'intersection de la tangente à l'hyperbole en $M_{0}$ avec la directrice $D$, le triangle $M_{0}FT$ est un triangle rectangle en $F$
4. Définition bifocale des ellipses et des hyperboles
4.1. Ellipses
$\centerdot\ \ $ Propriété 1 :
Soit $\mathcal{E}$ une ellipse de foyers $F$ et $F'$, de grand axe $[A'A]$, de centre $O$. Si on note $a=OA$, alors pour tout point $M$ de l'ellipse
$$MF+MF'=2a$$
$\centerdot\ \ $ Propriété 2 :
Etant donnés deux points $F$ et $F'$ tels que $FF'=2c$ et un réel $a>c$, l'ensemble des points $M$ du plan tels que $MF+MF'=2a$ est l'ellipse de foyers $F$ et $F'$ et dont la longueur du grand axe est égale à $2a$
$\centerdot\ \ $ Application : construction d'une ellipse : ovale des jardiniers
Pour tracer une ellipse, on peut fixer les extrémités d'une ficelle en deux points $(F et F')$, la ficelle étant de longueur $l=2a$ avec $l>FF'$. On peut ensuite faire coulisser un stylo le long de la ficelle tendue.
La position du stylo étant notée $M$, à tout instant on a $MF+MF'=l=2a$. Le stylo décrit bien l'ellipse de foyer $F$ et $F'$.
Ce principe est utilisé par les jardiniers pour tracer des parterres ovoïdes. Une corde étant attachée à ses extrémités à deux pieux, en faisant coulisser un morceau de bois, ils peuvent ainsi tracer un sillon dans le sol.
4.2. Hyperboles
$\centerdot\ \ $ Propriété 1 :
Soit $\mathcal{H}$ une hyperbole de foyers $F$ et $F'$, de sommets $A$ et $A'$, de centre $O$. Si on note $a=OA$, alors pour tout point $M$ de l'hyperbole
$$|MF-MF'|=2a$$
$\centerdot\ \ $ Propriété 2 :
Etant donnés deux points $F$ et $F'$ tels que $FF'=2c$ et un réel $0<a<c$, l'ensemble des points $M$ du plan tels que $|MF-MF'|=2a$ est l'hyperbole de foyers $F$ et $F'$ et dont la distance entre les sommets est égale à $2a$
V. Equation générale des coniques
Le plan étant rapporté à un repère orthonormé $(O\;;\ \vec{i}\;,\ \vec{j})$ : dans le cas le plus général, une conique $\Gamma$ est une courbe d'équation $P(x,\ y)=ax^{2}+2bxy+cy^{2}+2dx+2ey+f=0$ avec $(a,\ b,\ c,\ d,\ e)\neq (0,\ 0,\ 0,\ 0,\ 0)$
Différents cas se présentent : le plus triviale est celui où $(a,\ b,\ c)=(0,\ 0,\ 0)$, on obtient alors une droite (conique dégénérée)
1. Equation du type $P(x\;,\ y)=ax^{2}+cy^{2}+dx+ey+f=0$ avec $(a\;,\ c)\neq (0\;,\ 0)$
On se place ici dans le cas où dans l'équation, il n'y a pas de terme en $xy$, $(b=0)$
$\centerdot\ \ $ si $a=0$ et $d\neq 0$ ou si $c=0$ et $e\neq 0$, $\ \Gamma$ est une parabole (l'équation contient au moins un terme $x^{2}$, pas de terme en $y^{2}$ et un terme en $y$, ou l'équation contient au moins un terme en $y^{2}$, pas de terme en $x^{2}$ et un terme en $x$)
$\centerdot\ \ $ si $a\neq 0$ et $c\neq 0$
$-\ $ si $a=c$ (coefficient de $x^{2}$=coefficient de $y^{2}$) $\Gamma$ est un cercle, un point ou l'ensemble vide
$-\ $ si $a$ et $c$ sont de même signe alors $\Gamma$ est une ellipse, un point ou l'ensemble vide
$-\ $ si $a$ et $c$ sont de signe contraire alors $\Gamma$ est une hyperbole, ou deux droites
Quelques exemples représentatifs à étudier soigneusement :
$\centerdot\ \ $ Equation 1 : $\ 2x^{2}+x-3y+5=0$ $(e_{1})$ (l'équation contient au moins un terme en $x^{2}$, pas de terme en $y^{2}$ et un terme en $y$)
$(e_{1})$ $\Leftrightarrow$ $2\left(x^{2}+\dfrac{1}{2}x\right)=3y-5$
(on utilise ensuite la mise sous forme canonique c'est à dire qu'on écrit $x^{2}+\dfrac{1}{2}x$ sous la forme de $(x+\ldots)^{2}=$
\begin{eqnarray} (e_{1})&\Leftrightarrow&2\left[\left(x+\dfrac{1}{4}\right)^{2}-\dfrac{1}{16}\right]=3y-5\nonumber \\ &\Leftrightarrow&2\left(x+\dfrac{1}{4}\right)^{2}=3y-5+\dfrac{1}{8}\nonumber \\ &\Leftrightarrow&\left(x+\dfrac{1}{4}\right)^{2}=\dfrac{3}{2}\left(y-\dfrac{13}{8}\right)\nonumber \end{eqnarray}
Soit $I\left(\dfrac{-1}{4};\ \dfrac{13}{8}\right)$), si $M(x\;,\ y)$ dans le repère $(O\;;\ \vec{i}\;,\ \vec{j})$, alors $M(X\;,\ Y)$ dans $(I;\ \vec{i},\ \vec{j})$ avec $$\left\lbrace\begin{array}{lllll} X&=&x-x_{I}&=&x+\dfrac{1}{4}\\ Y&=&y-y_{I}&=&y-\dfrac{13}{8}\end{array}\right.$$
Donc dans le repère $(I\;;\ \vec{i}\;,\ \vec{j})$, l'équation devient $X^{2}=\dfrac{3}{2}Y$ ou $Y=\dfrac{3}{2}X^{2}$ la conique est donc une parabole d'axe $(IY)$ de sommet $I$
(remarque $X^{2}=\dfrac{3}{2}Y$ $\Longrightarrow$ $Y\geqslant 0$ donc $y\geqslant \dfrac{13}{8}$ la courbe est "au dessus" de la droite d'équation $y=\dfrac{13}{8}$)
$\centerdot\ \ $ Equation 2 : $\ 4x^{2}+2y^{2}+3x-y+1=0$ (termes en $x^{2}$ et en $y^{2}$ précédés de coefficients de même signe donc $\Gamma$ est une ellipse, un point ou l'ensemble vide)
$4x^{2}+2y^{2}+3x-y+1=0$ $\Longleftrightarrow$ $4\left(x^{2}+\dfrac{3}{4}x\right)+2\left(y^{2}-\dfrac{1}{2}y\right)+1=0$ (on utilise ensuite la mise sous forme canonique c'est à dire qu'on fait apparaître dans $(x^{2}+\dfrac{3}{4}x)$ un développement de $(x+\ldots)^{2}$ et idem avec $(y^{2}-\dfrac{1}{2}y)$
\begin{eqnarray} M(x\;,\ y)\in\Gamma&\Leftrightarrow&4\left[\left(x+\dfrac{3}{2}\right)^{2}-\dfrac{9}{4}\right]+2\left[\left(y-\dfrac{1}{4}\right)^{2}-\dfrac{1}{16}\right]+1=0\nonumber \\ &\Leftrightarrow&4\left(x+\dfrac{3}{2}\right)^{2}+2\left(y-\dfrac{1}{4}\right)^{2}=\dfrac{65}{8}\nonumber \end{eqnarray}
ou $\dfrac{32}{65}\left(x+\dfrac{3}{2}\right)^{2}+\dfrac{16}{65}\left(y-\dfrac{1}{4}\right)^{2}=1$
en multipliant par $\dfrac{8}{65}$ de manière à faire apparaître 1 dans le second membre
on a donc $M(x\;,\ y)\in \Gamma$ $\Longleftrightarrow$ $\dfrac{\left(x+\dfrac{3}{2}\right)^{2}}{\dfrac{65}{32}}+\dfrac{\left(y-\dfrac{1}{4}\right)^{2}}{\dfrac{65}{16}}=1$
ceci nous montre que la conique est une ellipse de centre $I\left(\dfrac{-3}{2}; \dfrac{1}{4}\right)$ (dans le repère $(I, \overrightarrow{i}, \overrightarrow{j})$,
l'équation deviendrait $\dfrac{X^{2}}{\dfrac{65}{32}}+\dfrac{Y^{2}}{\dfrac{65}{16}}=1$),
ellipse du type $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}$ avec $a<b$ ici $a=\sqrt{\dfrac{65}{32}}$, $b=\sqrt{\dfrac{65}{16}}=\dfrac{\sqrt{65}}{4}$ ellipse d'axe focal $(IY)$
$\centerdot\ \ $ Equation 3 : $3x^{2}+3y^{2}+6x-9y+1=0$ (coefficient de $x^{2}$=coefficient de $y^{2}$) $\Gamma$ est un cercle, un point ou l'ensemble vide
\begin{eqnarray} M(x\;,\ y)\in\Gamma&\Leftrightarrow&x^{2}+y^{2}+2x-3y+\dfrac{1}{3}=0\nonumber \\ &\Leftrightarrow&(x+1)^{2}-1+\left(y-\dfrac{3}{2}\right)^{2}-\dfrac{9}{4}+\dfrac{1}{3}=0\nonumber \\ &\Leftrightarrow&(x+1)^{2}+\left(y-\dfrac{3}{2}\right)^{2}=\dfrac{35}{12}\nonumber \end{eqnarray}
La conique est donc le cercle de centre $I\left(-1;\ \dfrac{3}{2}\right)$ et de rayon $\sqrt{\dfrac{35}{12}}$
$\centerdot\ \ $ Equation 4 : $-4x^{2}+2y^{2}+x-3y+1=0$
\begin{eqnarray} M(x\;,\ y)\in\Gamma&\Leftrightarrow&-4\left(x^{2}-\dfrac{1}{4}x\right)+2\left(y^{2}-\dfrac{3}{2}y\right)+1=0\nonumber \\ &\Leftrightarrow&-4\left[\left(x-\dfrac{1}{4}\right)^{2}-\dfrac{1}{16}\right]+2\left[\left(y-\dfrac{3}{2}\right)^{2}-\dfrac{9}{4}\right]+1=0\nonumber \\ &\Leftrightarrow&-4\left(x\frac{1}{4}\right)^{2}+2\left(y-\dfrac{3}{2}\right)^{2}=\dfrac{13}{4}\nonumber \\ &\Leftrightarrow&-\dfrac{\left(x-\dfrac{1}{4}\right)^{2}}{\dfrac{13}{16}}+\dfrac{\left(y-\dfrac{3}{2}\right)^{2}}{\dfrac{13}{8}}=1\nonumber \end{eqnarray}
avec $\left\{
\begin{array}{lcl}
X &=& x-\dfrac{1}{4}\\
\\
Y &=& y-\dfrac{3}{2}
\end{array}
\right.$
(c'est à dire en prenant $I\left(\dfrac{1}{4}; \dfrac{3}{2}\right)$ comme nouvelle origine, on obtient
$-\dfrac{X^{2}}{\dfrac{13}{16}}+\dfrac{Y^{2}}{\dfrac{13}{8}}=1$)
Soit une équation du type $-\dfrac{X^{2}}{a^{2}}+\dfrac{Y^{2}}{b^{2}}=1$ avec $a<b$ ici $a=\sqrt{\dfrac{13}{16}}$, $b=\sqrt{\dfrac{13}{8}}$
La conique est donc une hyperbole de centre $I$, d'axe focal $(Iy)$ dont les asymptotes ont pour équation, asymptotes $Y=\pm \sqrt{2}X$ soit $y-\dfrac{3}{2}=\pm \sqrt{2}\left(x-\dfrac{1}{4}\right)$ avec $c=\sqrt{a^{2}+b^{2}}=\sqrt{\dfrac{39}{16}}=\dfrac{\sqrt{39}}{4}$,
les foyers $F\left(0,\ Y=\dfrac{\sqrt{39}}{4}\right)$ et $F'\left(0,\ Y=-\dfrac{\sqrt{39}}{4}\right)$
Directrices $D$, $\ D'$ $Y=\pm \dfrac{13}{8}\times \dfrac{4}{\sqrt{39}}=\pm \dfrac{\sqrt{13}}{2\sqrt{3}}$

2. Equation du type $P(x\;,\ y)=ax^{2}+2bxy+cy^{2}+2dx+2ey+f=0$ avec $b\neq 0$
La différence par rapport au paragraphe précédent vient du fait que l'équation contient un terme en $xy$.
Mais, en fait, on peut toujours se ramener au cas où $b=0$, ceci par un changement de repère bien choisi (cf.paragraphe 22)
2.1. Approche rapide : équation aux pentes
Considérons $P(x\;,\ y)=\underbrace{ax^{2}+2bxy+cy^{2}}_{A(x,\ y)}+\underbrace{2dx+2ey+f}_{B(x,\ y)}$
De la même manière que pour une fonction, pour déterminer les pentes des asymptotes obliques (directions asymptotiques) il faut d'abord chercher $\lim_{x\to \pm \infty} \dfrac{f(x)}{x}$, ici, on fait apparaître l'expression $m=\dfrac{y}{x}$ et on s'intéresse au comportement de l'expression quand $x$ et $y$ tendent vers l'infini, leur rapport $m$ restant constant
En divisant par $x^{2}$ l'équation initiale, cela donne
$a+2b\left(\dfrac{y}{x}\right)+c\left(\dfrac{y}{x}\right)^{2}+2d\left(\dfrac{1}{x}\right)+2e\left(\dfrac{y}{x^{2}}\right)+f\left(\dfrac{1}{x^{2}}\right)=0$
On a donc $\dfrac{A(x,\ y)}{x^{2}}=a+2b\left(\dfrac{y}{x}\right)+c\left(\dfrac{y}{x}\right)^{2}=cm^{2}+2bm+a$
On ne considère que $a+2b\left(\dfrac{y}{x}\right)+c\left(\dfrac{y}{x}\right)^{2}=cm^{2}+2bm+a$, les autres devenant négligeables.
Méthode :
On étudie l'équation du second degré : $cm^{2}+2bm+a=0$ (équation aux pentes)
$\centerdot\ \ $ si $B(x,\ y)\neq 0$ ($B(x,\ y)=2dx+2ey+f$)
Discussion selon les racines de : $cm^{2}+2bm+a=0$
$-\ $ si l'équation n'a pas de racine : il n'a pas de branches à l'infini, la conique est une ellipse
$-\ $ si l'équation a 2 racines distinctes $m_{1}$ et $m_{2}$ : il y a 2 branches à l'infini, la conique est une hyperbole d'asymptotes de pentes $m_{1}$ et $m_{2}$
$-\ $ si l'équation a une racine double $m_{1}$ alors, il n'a qu'une branche à l'infini, la conique est une parabole d'axe de pente $m_{1}$
Exemple :
$x^{2}+y^{2}-2xy+2x+y+1=0$, on divise par $x^{2}$ l'équation initiale
$1+\dfrac{y^{2}}{x^{2}}-2\frac{y}{x}+2\frac{1}{x}+\dfrac{y}{x^{2}}+\dfrac{1}{x^{2}}=0$
l'équation aux pentes est $m^{2}-2m+1=0$ soit $(m-1)^{2}=0$ il y a 1 racine double $m=1$.
C'est une parabole dont l'axe est parallèle à la de pente $m(m-1)$, soit $y=x$
$\centerdot\ \ $ si $B(x,\ y)=0\ $ ($B(x,\ y)=2dx+2ey+f$)
$P(x,\ y)=ax^{2}+2bxy+cy^{2}=0$, discussion selon les racines de : $cm^{2}+2bm+a=0$
$-\ $ si l'équation n'a pas de racine : il n'a pas de points qui vérifient l'équation $P(x,\ y)=ax^{2}+2bxy+cy^{2}=0$
$-\ $ si l'équation a 2 racines distinctes $m_{1}$ et $m_{2}$ : la conique est dégénérée on a deux droites d'équation $y=m_{1}$ et $y=m_{2}$
$-\ $ si l'équation a une racine double $m_{1}$ la conique est dégénérée on a une droite d'équation $y=m_{1}$
Exemple :
$6x^{2}-xy-y^{2}=0$, l'équation aux pentes est $-m^{2}-m+6=0$, elle admet $m=2$ et $m=-3$ comme solution donc l'ensemble des points qui vérifient $6x^{2}-xy-y^{2}=0$ est la réunion des deux droites d'équation $y=2x$ et $y=-3x$
(cf. autre méthode en exercice)
2.2. Centre de la conique
On se place ici dans le cas où la conique est non dégénérée $B(x,\ y)=2dx+2ey+f\neq 0$
Dans le cas où la conique est une conique à centre (cercle, ellipse, hyperbole) :
Les coordonnées $x_{0}$ et $y_{0}$ du centre sont solution de : $\dfrac{\partial P(x,\ y)}{\partial x}=0$ et $\dfrac{\partial P(x,\ y)}{\partial y}=0$
Si ce système n'a pas de solution, la conique est une parabole
Exemple :
pour $x^{2}+y^{2}-2xy+y+1=0$, le système s'écrit
$$\left\{
\begin{array}{lcl}
2x-2y+2 &=& 0\\
2y-2x+1 &=& 0
\end{array}
\right.$$
Le système n'a pas de solution donc la conique est une parabole.
2.3. Axes de symétrie d'une hyperbole :
Les axes de symétrie d'une hyperbole sont les bissectrices des asymptotes, ils font un angle $\varphi$ et $\varphi +\dfrac{\pi}{2}$ avec les axes de coordonnées avec
$\tan 2\varphi=\dfrac{m_{1}+m_{2}}{1-m_{1}m_{2}}=\dfrac{2b}{a-c}$
ils passent par le centre $(x_{0},\ y_{0})$ de l'hyperbole, d'où leur équation :
$\dfrac{y-y_{0}}{x-x_{0}}=tg\varphi$ $\quad$ et $\quad$ $\dfrac{y-y_{0}}{x-x_{0}}=\dfrac{-1}{tg\varphi}$
VI. Paramétrages et coordonnées polaires
1. Représentations paramétriques des coniques
$\centerdot\ \ $ Un paramétrage d'un cercle $C$ de centre $O$ et de rayon $R$ est
$$\left\{
\begin{array}{lll}
x &=& R\cos\theta \\
y &=& R\sin\theta
\end{array}
\right.\ \theta\in [-\pi; \pi[$$
cela signifie qu'un point $M(x,\ y)$ appartient à $C$ si et seulement si il existe
un réel $\theta$ de $[-\pi;\ \pi[$ tel que $$\left\{
\begin{array}{lll}
x &=& R\cos\theta \\
y &=& R\sin\theta
\end{array}
\right.$$
$\centerdot\ \ $ Un paramétrage d'un cercle $C$ de centre $I(x_{0};\ y_{0})$ et de rayon $R$ est
$$\left\{
\begin{array}{lll}
x &=& x_{0}+R\cos\theta \\
y &=& y_{0}+R\sin\theta
\end{array}
\right.\ \theta\in [-\pi;\ \pi[$$
$\centerdot\ \ $ Un paramétrage d'une ellipse de centre $O$ d'équation $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ est
$$\left\{
\begin{array}{lll}
x &=& a\cos\theta \\
y &=& b\sin\theta
\end{array}
\right.\ \theta\in [-\pi;\ \pi[$$
$\centerdot\ \ $ Un paramétrage d'une ellipse de centre $I(x_{0},\ y_{0})$ d'équation $\dfrac{(x-x_{0})^{2}}{a^{2}}+\dfrac{(y-y_{0})^{2}}{b^{2}}=1$ est $$\left\{
\begin{array}{lll}
x &=& x_{0}+a\cos\theta \\
y &=& y_{0}+b\sin\theta
\end{array}
\right.\ \theta\in [-\pi;\ \pi[$$
$\centerdot\ \ $ Un paramétrage d'une parabole d'équation $y^{2}=2px$ est
$$\left\{
\begin{array}{lll}
x &=& \dfrac{t^{2}}{2p} \\
y &=& t
\end{array}
\right.\ t\in \mathbf{R}$$
$\centerdot\ \ $ Un paramétrage d'une hyperbole d'équation $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{b^{2}}=1$ est
$$\left\{
\begin{array}{lll}
x &=& cht \\
y &=& sht
\end{array}
\right.\ t\in \mathbf{R}$$
2. Equation polaire d'une conique, l'origine étant au foyer
Soit $O$ point origine, soit $D$ une droite passant par $O$,
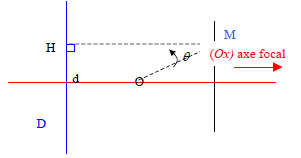
choisissons $(Ox)$ orthogonale à $D$. Soit $d$ le réel tel que
l'équation de $D$ peut s'écrire $x=d$.
Un point $M$ appartient à la conique de foyer $O$ et d'excentricité $e$ ($e>0$)
et de directrice $D$ si $OM=eMH$ ($MF=eMH$ où $F$ foyer) qui équivaut à $OM^{2}=e^{2}MH^{2}$
Cette égalité donne en coordonnées polaires : $\ r^{2}=e^{2}(rcos\theta -d)^{2}$ d'où
$r=\pm e(rcos\theta -d)$, on obtient en résolvant en $r$,
$r=\dfrac{ed}{1+ecos\theta}$ ou $r=\dfrac{ed}{1-ecos\theta}$
Ces deux équations représentent la même courbe : il suffit de changer $\theta$ en $\pi -\theta$ pour s'en convaincre
L'équation de la conique de foyer $O$, de directrice $D$ $x=d$, et d'excentricité $e$ est donc
$r=\dfrac{ed}{1+ecos\theta}$
Propriété :
Soient $p$ et $e$ deux réels positifs. La courbe d'équation polaire
$r=\dfrac{p}{1+ecos\theta}$ est une conique non dégénérée d'excentricité $e$ et de foyer $O$.
VII Image d'une ellipse par affinité
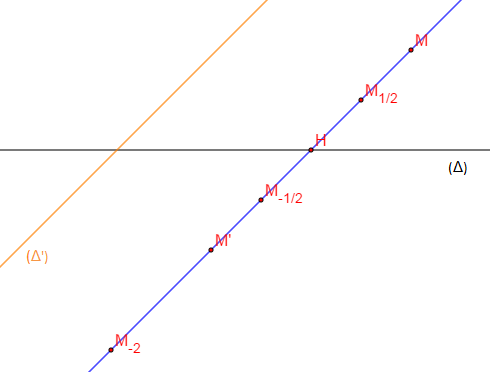
On appelle affinité d'axe $(\Delta)$ de rapport $k\in\mathbb{R}^{*}\setminus\{1\}$ de direction $(\Delta')$, la transformation du plan qui laisse tout point de $(\Delta)$ invariant et qui associe à tout point $M\notin(\Delta)$, le point $M'$ tel que :
$\overrightarrow{HM'}=k\overrightarrow{HM}$, où $H$ est le projeté de $M$ sur $(\Delta)$ parallèlement à $(\Delta')$.
$M_{-2}$ est l'image de $M$ par l'affinité d'axe $(\Delta)$ de direction $(\Delta')$ et de rapport $k=-2$.
$M_{1/2}$ est l'image de $M$ par l'affinité d'axe $(\Delta)$ de direction $(\Delta')$ et de rapport $k=\dfrac{1}{2}$.
Remarques :
Si $(\Delta)\perp(\Delta')$, on parle d'affinité perpendiculaire d'axe $(\Delta)$ et de rapport $k$.
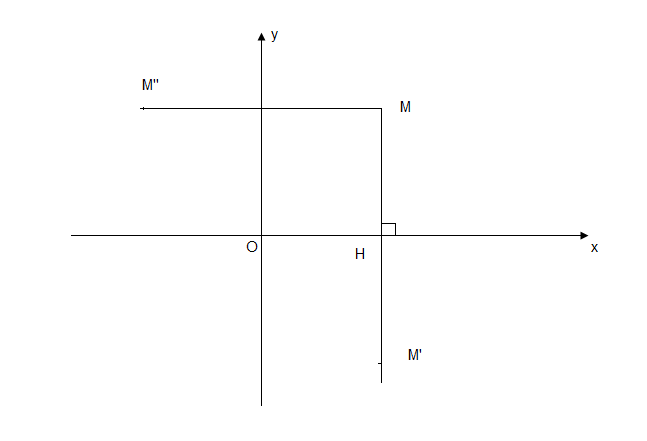
$\centerdot\ \ $ Affinité perpendiculaire d'axe $(x'Ox)$ et de rapport $k$.
Soient $M\begin{pmatrix}
x\\
y
\end{pmatrix}$ et $M'\begin{pmatrix}
x'\\
y'
\end{pmatrix}$, on a $\overrightarrow{HM}'\begin{pmatrix}
0\\
y'-0
\end{pmatrix}$ et $\overrightarrow{HM}\begin{pmatrix}
0\\
y
\end{pmatrix}$
Donc $\overrightarrow{HM'}=k\overrightarrow{HM} \ \Leftrightarrow \ \left\{
\begin{array}{lcl}
x' &=& x \\
y' &=& ky
\end{array}
\right.$
$\centerdot\ \ $ De même, l'affinité perpendiculaire d'axe $(y'Oy)$ et de rapport $k$ est donnée par :
$$\left\{
\begin{array}{lcl}
x' &=& kx \\
y' &=& y
\end{array}
\right.$$
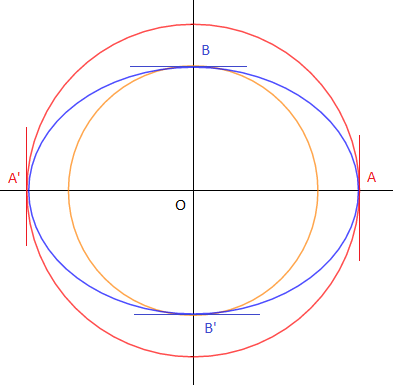
$\centerdot\ \ $ Soit l'ellipse de grand axe $[AA']$, de petit diamètre $[BB']$ et d'équation : $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$.
$\centerdot\ \ $ l'affinité perpendiculaire d'axe $(x'Ox)$ et de rapport $\dfrac{a}{b}$ est donnée par :
$$\left\{
\begin{array}{lcl}
x' &=& x \\
y' &=& \dfrac{a}{b}y
\end{array}
\right.$$
$\centerdot\ \ $ l'affinité perpendiculaire d'axe $(y'Oy)$ et de rapport $\dfrac{b}{a}$ est donnée par :
$$\left\{
\begin{array}{lcl}
x' &=& \dfrac{b}{a}x \\
y' &=& y
\end{array}
\right.$$
$\centerdot\ \ $ L'image de l'ellipse par l'affinité perpendiculaire d'axe $(x'Ox)$ et de rapport $\dfrac{a}{b}$ est le cercle de diamètre $[AA']$
$\centerdot\ \ $ L'image de l'ellipse par l'affinité perpendiculaire d'axe $(y'Oy)$ et de rapport $\dfrac{b}{a}$ est le cercle de diamètre $[BB']$
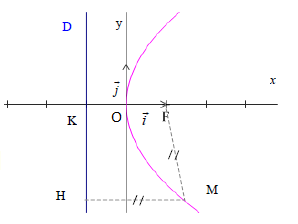




Commentaires
Ahmat Hassan Yerima (non vérifié)
dim, 03/17/2019 - 18:49
Permalien
les exercises de maths
Ajouter un commentaire