Les angles - T S1
I Angles orientés de demi-droites
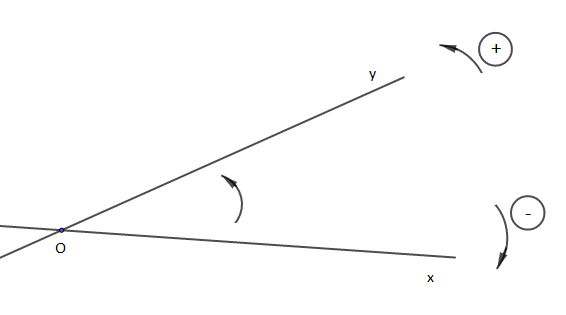
Soient $[Ox)$ et $[Oy)$ deux demi-droites de même origine $O$. L'angle orienté de demi-droites $\left(\widehat{[Ox)\;,\ [Oy)}\right)$ est l'angle qui a pour sommet $O$, pour origine $[Ox)$ et pour extrémité $[Oy).$
II Angles orientés de vecteurs
II.1 Définitions
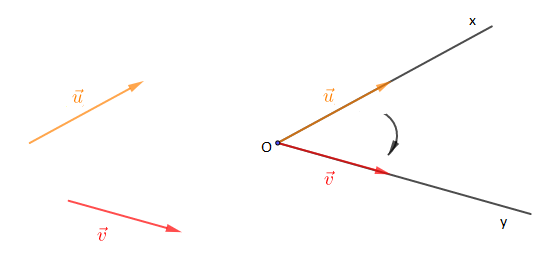
Soient $\vec{u}$ et $\vec{v}$ deux vecteurs, $O$ un point du plan, $[Ox)$ et $[Oy)$ deux demi-droites tels que $\vec{u}$ soit un vecteur directeur de $[Ox)$ et $\vec{v}$ celui de $[Oy)$. L'angle orienté des vecteurs $\vec{u}$ et $\vec{v}$ est noté $\left(\vec{u}\;,\ \vec{v}\right)=\left(\widehat{[Ox)\;,\ [Oy)}\right)$
II.2 Propriétés
$\centerdot\ \ $ $\left(\vec{u},\ \vec{v}\right)=-\left(\vec{v}\;,\ \vec{u}\right)\ (2\pi)$
$\centerdot\ \ $ $(k\vec{u}\;,\ k\vec{v})=\left(\vec{u}\;,\ \vec{v}\right)(2\pi) \quad \forall\;k\neq 0$
$\centerdot\ \ $ $(k\vec{u},\ \vec{v})=\left\lbrace\begin{array}{ll}\left(\vec{u}\;,\ \vec{v}\right)\ (2\pi) & \mbox{ si $k>0$}\\\pi +\left(\vec{u}\;,\ \vec{v}\right)\ (2\pi) & \mbox{ si $k<0$}\end{array}\right.$
$\centerdot\ \ $ $\left(\vec{u}\;,\ \vec{v}\right)+\left(\vec{v}\;,\ \vec{w}\right)=\left(\vec{u}\;,\ \vec{w}\right)\ (2\pi)$
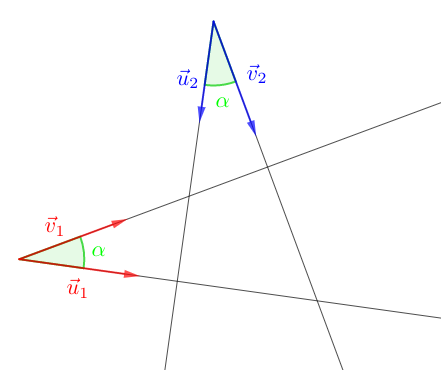
$\centerdot\ \ $ $\vec{u}_{1}\perp\vec{u}_{2}\ $ et $\ \vec{v}_{1}\perp\vec{v}_{2}\ $ alors, $\ \left(\vec{u}_{1},\ \vec{v}_{1}\right)=\left(\vec{u}_{2},\ \vec{v}_{2}\right)\ (\pi)$
III Angles orientés de droites
III.1 Définitions
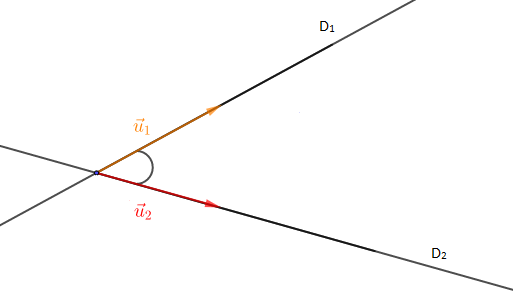
Soient deux droites $D_{1}\ $ et $\ D_{2}$ de vecteurs directeurs respectifs $\vec{u}_{1}\ $ et $\ \vec{u}_{2}$. L'angle orienté de droites $\vec{u}_{1}\ $ et $\ \vec{u}_{2}$ noté $\left(\widehat{(D_{1})\;,\ (D_{2})}\right)=\left(\vec{u}_{1}\;,\ \vec{u}_{2}\right)\ (\pi)$
III.2 Bissectrices
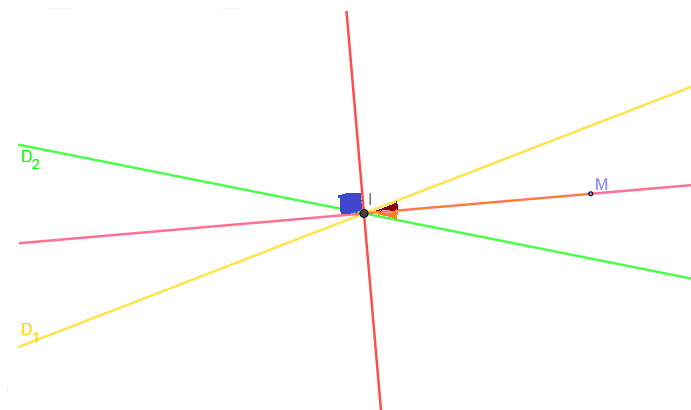
Soient $D_{1}\ $ et $\ D_{2}$ telles que $D_{1}\cap D_{2}=\{I\}.$
Une bissectrice de $(D_{1}\;,\ D_{2})$ est l'ensemble des points équidistants de $D_{1}\ $ et $\ D_{2}$. C'est aussi l'ensemble des points $M$ tels que $(D_{1}\;,\ IM)=(IM\;,\ D_{2}).$ On a deux bissectrices qui sont perpendiculaires.
IV Cocyclicité
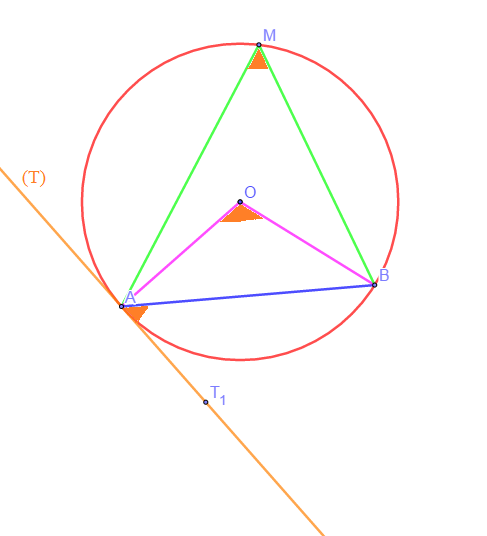
Soit $\mathcal{C}$ un cercle de centre $O\;,\ A\ $ et $\ B$ deux points de $\mathcal{C}\ $ et $\ \mathcal{T}$ la tangente en $A\ $ à $\ \mathcal{C}$. On a :
$\left(\overrightarrow{MA}\;,\ \overrightarrow{MB}\right)$ est un angle inscrit qui intercepte l'arc $\overset{\displaystyle\frown}{AB}$.
$\left(\overrightarrow{OA}\;,\ \overrightarrow{OB}\right)$ est un angle au centre qui intercepte l'arc $\overset{\displaystyle\frown}{AB}$.
$\left(\overrightarrow{MA}\;,\ \overrightarrow{MB}\right)=\dfrac{1}{2}\left(\overrightarrow{OA}\;,\ \overrightarrow{OB}\right)\ (2\pi)=\left(\overrightarrow{AT_{1}}\;,\ \overrightarrow{AB}\right)$ où $T_{1}\in\mathcal{T}.$
Théorème
$\centerdot\ \ $ si $M\ $ et $\ N$ $\in\mathcal{C}$ alors $$\left(\overrightarrow{MA}\;,\ \overrightarrow{MB}\right)=\left(\overrightarrow{NA}\;,\ \overrightarrow{NB}\right)\ (\pi)$$
$\centerdot\ \ $ si $\left(\overrightarrow{MA}\;,\ \overrightarrow{MB}\right)\ $ et $\ \left(\overrightarrow{NA}\;,\ \overrightarrow{NB}\right)$ interceptent le même arc alors $$\left(\overrightarrow{MA}\;,\ \overrightarrow{MB}\right)=\left(\overrightarrow{NA}\;,\ \overrightarrow{NB}\right)\ (2\pi)$$
$\centerdot\ \ $ Les points $A\;,\ B\;;\ C\ $ et $\ D$ sont cocycliques (appartiennent à un même cercle $\mathcal{C}$) ou alignés si, et seulement si, $$\left(\overrightarrow{BC}, \overrightarrow{BD}\right)=\left(\overrightarrow{CA}\;,\ \overrightarrow{CD}\right)\ (\pi)$$
Auteur:
Seyni Ndiaye & Diny Faye

Commentaires
Abdourahmane Ba (non vérifié)
mar, 06/21/2022 - 20:24
Permalien
je veut apprendre Mathématique
Ajouter un commentaire