Vous êtes ici

Amplificateur opérationnel : montages dérivateur et intégrateur - 1er s

Classe:

Première

L'Amplificateur Opérationnel a été initialement conçu pour effectuer des calculs mathématiques dans les calculateurs analogiques.

Il est aujourd'hui miniaturisé dans un circuit intégré composé d'une vingtaine de transistors.

Il est d'un emploi très courant en électronique

Ce chapitre se consacre aux fonctions de dérivation et d'intégration de l'amplificateur opérationnel

$(AOP)$

I. Types de montages

1. Dérivateur

1.1. Schéma du montage

Un circuit dérivateur de base avec amplificateur opérationnel se fait en mettant un condensateur sur la liaison d'entrée.

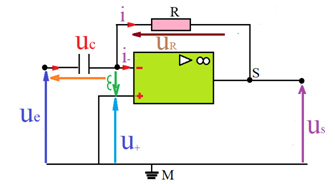
1.2. Expression de la tension de sortie Vs(t)

$L'AOP$ étant considéré comme parfait

La loi des mailles appliquée à l'entrée de

$l'AOP$ s'écrit :

$\begin{array}{rcl} u_{e}-u_{c}+\varepsilon+u_{+}&=&0\\\Rightarrow\;u_{e}-u_{c}+0+0&=&0\\u_{e}&=&u_{c} \end{array}$

La loi des mailles appliquée à la sortie de

$l'AOP$ s'écrit :

$\begin{array}{rcl} u_{S}+u_{R}+\varepsilon-u_{+}&=&0\\\Rightarrow\;u_{S}&=&-u_{R}\\\text{Comme }u_{R}=Ri\quad\text{et}\quad i=\dfrac{\mathrm{d}q}{\mathrm{d}t}=\dfrac{\mathrm{d}Cu_{c}}{\mathrm{d}t}=C\dfrac{\mathrm{d}u_{c}}{\mathrm{d}t}\\u_{e}&=&u_{c}\\\Rightarrow\boxed{u_{S}=-RC\dfrac{\mathrm{d}u_{e}}{\mathrm{d}t}} \end{array}$

$RC$ est une constante de temps.

La tension de sortie du montage est proportionnelle à la dérivée de la tension d'entrée.

Ce montage dérive une tension d'entrée.

2. Intégrateur

2.1. Schéma du montage

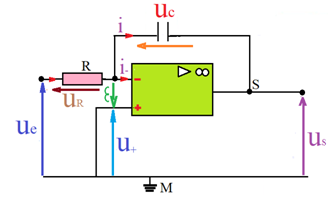
Un circuit intégrateur de base avec amplificateur opérationnel se fait en mettant un condensateur sur la boucle de rétroaction.

2.2. Expression de la tension de sortie $Vs(t)$

$L'AOP$ étant considéré comme parfait.

La loi des mailles appliquée à l'entrée de

$l'AOP$ s'écrit :

$\begin{array}{rcl} u_{e}-u_{R}+\varepsilon+u_{+}&=&0\\\Rightarrow\;u_{e}-u_{R}+0+0&=&0\\u_{R}&=&u_{e}\\\Rightarrow\;Ri&=&u_{e}\\\Rightarrow\;i&=&\dfrac{u_{e}}{R} \end{array}$

La loi des mailles appliquée à la sortie

$l'AOP$ s'écrit :

$\begin{array}{rcl} u_{S}+u_{c}+\varepsilon-u_{+}&=&0\\\Rightarrow\;u_{S}+0+0&=&0\\\Rightarrow\;u_{S}&=&-u_{c}\\\text{Comme }u_{c}=\dfrac{q}{C}\quad\text{et}\quad q=\int\;i\mathrm{d}t\\&=&\dfrac{1}{C}\int\dfrac{u_{e}}{R}\mathrm{d}t\\&=&\dfrac{1}{RC}\int\;u_{e}\mathrm{d}t\\u_{e}&=&u_{c}\\\Rightarrow\boxed{u_{S}=-\dfrac{1}{RC}\int\;u_{e}\mathrm{d}t} \end{array}$

$RC$ est une constante de temps.

La tension de sortie du montage est proportionnelle à l'intégrale de la tension d'entrée :

Ce montage intègre une tension d'entrée.

II. Applications

1. Visualisations des tensions à l'oscilloscope

1.1. Cas d'une tension triangulaire à l'entrée

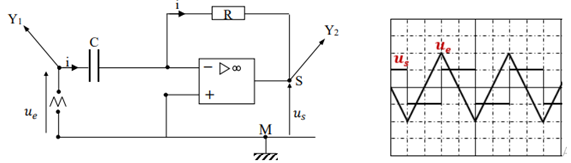
Si la tension d'entrée

$u_{e}$ est un signal triangulaire, la tension de sortie

$u_{S}$ est un signal carré

1.2. Cas d'une tension créneau à l'entrée

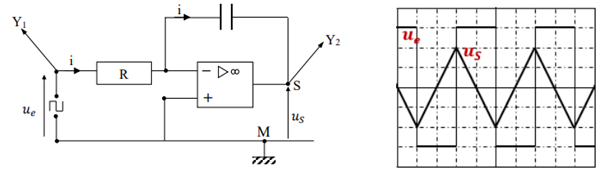
La réponse à une tension d'entrée

$u_{e}$ rectangulaire est une tension de sortie

$u_{S}$ triangulaire

2. Intérêt des montages

$-\$ Un montage dérivateur permet de transformer une tension d'entrée en sa dérivée.

$-\$ Un montage intégrateur permet de transformer une tension d'entrée en primitive.

Auteur:

Sidy Mouhamed Ndiaye

Commentaires

Anonyme (non vérifié)

mar, 04/01/2025 - 17:06

Permalien

C'est magnifique l

C'est magnifique l'exploitation

répondre

Ajouter un commentaire

form.antibot { display: none !important; } You must have JavaScript enabled to use this form.

Vous êtes ici

Amplificateur opérationnel : montages dérivateur et intégrateur - 1er s

Formulaire de recherche

I. Types de montages

1. Dérivateur

1.1. Schéma du montage

1.2. Expression de la tension de sortie Vs(t)

2. Intégrateur

2.1. Schéma du montage

2.2. Expression de la tension de sortie Vs(t)Vs(t)

II. Applications

1. Visualisations des tensions à l'oscilloscope

1.1. Cas d'une tension triangulaire à l'entrée

1.2. Cas d'une tension créneau à l'entrée

2. Intérêt des montages

Commentaires

C'est magnifique l

Ajouter un commentaire

Plain text

2.2. Expression de la tension de sortie $Vs(t)$