Condensateurs : capacité, énergie emmagasinée - 1er s
Classe:
Première
Moins nombreux que les résistances, les condensateurs sont cependant très répandus dans les montages électroniques.
A l'inverse des résistances qui sont presque toutes identiques, les condensateurs ont des formes et des encombrements très divers.
Cela s'explique par les technologies variées qui conviennent aux différentes applications de ces éléments.
I. Condensateur
1. Constitution et représentation symbolique
Un condensateur est constitué de deux surfaces conductrices appelées armatures séparées par un isolant appelé matériau diélectrique (air, plastique...)
Sa représentation symbolique est :
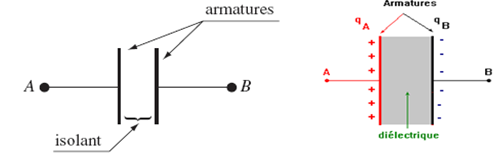
2. Exemples de condensateurs
Il existe des condensateurs de différentes tailles, formes, et de différents matériaux conducteurs et/ou diélectriques qui possèderont tous la même représentation symbolique.
Le condensateur est dit « plan » si ses armatures sont planes et parallèles.
A l'intérieur d'un condensateur plan, il existe un champ électrique uniforme de valeur constante.
II. Charge et décharge du condensateur
1. Dispositif expérimental
Considérons le montage comportant un galvanomètre, un générateur de force électromotrice (f.é.m.) E, un interrupteur simple allumage et le condensateur.
Remarque :
Le galvanomètre mesure les quantités d'électricité traversant son cadre, dans un sens comme dans l'autre.
2. Charge d'un condensateur
2.1. Expérience
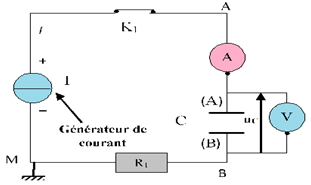
On utilise un générateur source de tension continue de force éléctromotrice $E$ et on réalise le montage suivant :
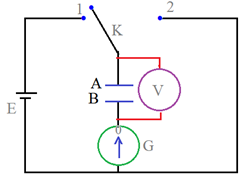
On utilise dans cette expérience un galvanomètre ou un ampèremètre à zéro centrale.
On bascule l'interrupteur $K$ à la position (1).
On observe que l'ampèremètre indique le passage d'un courant électrique durant un temps très court et que le voltmètre indique que la tension aux bornes du condensateur $U_{AB}=E.$
On dit que le condensateur est chargé et le courant électrique qui passe dans le circuit s'appelle courant de charge.
2.2. Interprétation
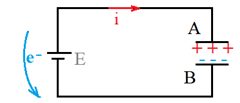
Le courant de charge résulte d'un déplacement des électrons de l'armature $A$ vers l'armature $B$ du condensateur, et à cause de l'existence du diélectrique entre les armatures, les électrons s'accumulent sur l'armature $B.$
L'armature $A$ perd le même nombre d'électrons gagnés par l'armature $B$ et condensateur devient chargé.
On appelle charge $"q"$ du condensateur, la valeur absolue de la quantité d'électricité que porte chaque armature $q=q_{A}=-q_{B}$
Une fois chargé, le condensateur conserve la charge électrique $"q"$ sur ses armatures et la tension $u_{AB}=E$ entre ses bornes, même lorsqu'on le débranche
3. Décharge d'un condensateur
3.1. Expérience
Lorsque le condensateur est chargé on bascule l'interrupteur $K$ à la position (2).
On constate la déviation de l'aiguille du galvanomètre dans le sens contraire pendant un temps très court et le voltmètre indique une annulation rapide de la tension aux bornes du condensateur.
3.2. Interprétation
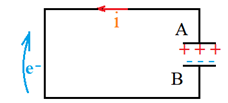
En déplaçant l'interrupteur à la position (2) on relie les armatures entre elles .Les électrons accumulés sur l'armature $B$ reviennent à l'armature $A$ et un courant de décharge apparait dans le circuit dans le sens inverse du courant de charge.
Lorsque le condensateur se décharge, la tension entre ses bornes est nulle.
4. Relation entre la charge et l'intensité
L'intensité du courant électrique est le débit de porteurs de charges qui traverse la section du conducteur par unité de temps.
Lorsque le courant est continu : $I=\dfrac{Q}{t}$
Lorsque le courant est variable : $i=\dfrac{\mathrm{d}q}{\mathrm{d}t}$
Dans le cas d'un condensateur : $i=\dfrac{\mathrm{d}q_{A}}{\mathrm{d}t}=\dfrac{\mathrm{d}q}{\mathrm{d}t}$ ; $q$ étant la charge portée par l'armature qui porte la charge
II. Capacité du condensateur
1. La charge du condensateur à courant constant
Le condensateur est initialement déchargé.
Le générateur délivre un courant d'intensité constante $I$
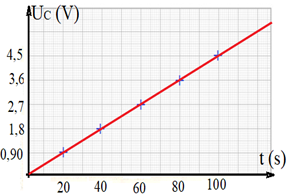
$$\begin{array}{|l|c|c|c|c|c|c|} \hline u_{C}\ (V)&0&20&40&60&80&100\\ \hline t\ (s)&0.00&0.90&1.8&2.7&3.6&4.5\\ \hline \end{array}$$
Observations :
On ferme l'interrupteur $K_{1}$ et on relève l'évolution de la tension $u_{c}$ aux bornes du générateur en fonction du temps.
Exploitation :
Traçons le graphe représentation la tension aux bornes du condensateur en fonction du temps
La courbe obtenue est une est une droite qui passe par l'origine : $u_{c}$ est donc proportionnelle à $t.$
On peut alors écrire : $u_{c}=u_{AB}=kt$ (1)
La quantité d'électricité $q$ mise en jeu pendant la charge du condensateur et l'intensité du courant $I$ en régime permanent : $q=It.$ (2)
Des relations (1) et (2), on tire :
$\begin{array}{rcl} t&=&\dfrac{u_{c}}{k}\\&=&\dfrac{q}{I}\\\Rightarrow\;q&=&\dfrac{I}{k}u_{c} \end{array}$
D'où la relation : $\boxed{q=Cu_{c}}$
$q$ en coulombs $(C)$
$u_{c}$ en volts $(V)$
$C$ en farads $(F)$
La charge d'un condensateur est proportionnelle à la tension $U_{C}$ entre les armatures.
Le coefficient de proportionnalité dépend des propriétés du condensateur.
Il caractérise sa capacité à acquérir une certaine charge
2. Capacité d'un condensateur plan
La valeur de la capacité $C$ ne dépend que des caractéristiques de l'élément capacitif (nature du diélectrique isolant, surface des armatures, distance entre elles...)
Exemple : pour un condensateur plan : $\boxed{C=\dfrac{\varepsilon S}{e}}$
$S$ : aire de la surface des armatures en $m^{2}$
$e$ : distance entre les armatures en $m$ et $C$ en $F$
$\varepsilon$ : permitivité absolue de l'isolant en $F\cdot m^{-1}$
On pose : $\varepsilon=\varepsilon_{r}\varepsilon_{0}$ avec $\varepsilon_{0}$ permittivité du vide et $\varepsilon_{r}$ $r$ sans dimension appelée permittivité relative qui
3. Association de condensateurs
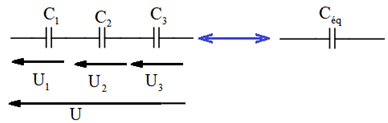
3.1. Association en série
$\begin{array}{rcl} Q&=&Q_{1}+Q_{2}+Q_{3}\\\Rightarrow\;Q&=&C_{1}U+C_{2}U+C_{3}U\\\Rightarrow\dfrac{Q}{U}&=&C_{1}+C_{2}+C_{3}\\\Rightarrow\boxed{C_{éq}=C_{1}+C_{2}+C_{3}} \end{array}$
Pour $n$ condensateurs : $$C_{éq}=C_{1}+C_{2}+C_{3}+\ldots\ldots C_{n}\Rightarrow\boxed{C_{éq}=\sum_{i=1}^{n}C_{i}}$$
La capacité équivalente à un groupement de condensateurs en parallèle est égale à la somme des capacités des différents condensateurs :
Remarque :
L'association en parallèle permet d'obtenir une capacité plus importante que celles des condensateurs utilisés dans le groupement.
4. Limite d'utilisation d'un condensateur
4.1. Tension nominale
C'est la tension supportable par le condensateur.
Elle permet un fonctionnement adéquat du condensateur.
4.2. Tension de claquage
C'est la tension limite au-delà de laquelle, le condensateur est détruit.
Le diélectrique perd ainsi son caractère d'isolant.
4.3. Champ disruptif
Le champ disruptif est le champ électrostatique au-delà duquel le diélectrique perd son caractère isolant.
Ce champ n'est pas supportable par le condensateur.
$\boxed{E_{d}=\dfrac{U_{c}}{d}}$ Avec $U_{c}$ : tension de claquage et d'épaisseur du diélectrique.
III. Énergie emmagasinée
1. Énergie stockée dans le condensateur
1.1. Mise en évidence expérimentale
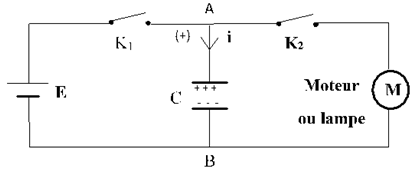
$\bullet\ $L'interrupteur $K_{2}$ restant ouvert, on ferme l'interrupteur.
Le condensateur se charge.
$\bullet\ $On ouvre $K_{1}$ et on ferme
Le condensateur se décharge dans le moteur (la lampe) qui tourne (s'allume)
Le condensateur avait donc emmagasiné de l'énergie qu'il a restituée au moteur (lampe) au cours de sa décharge.
3.2. Expression de l'énergie emmagasinée
On démontre que l'énergie d'un condensateur chargé sous une tension $U$ est donnée par la relation :
$$\boxed{E_{c}=\dfrac{1}{2}Cu^{2}\quad\text{ou}\quad E_{c}=\dfrac{1}{2}\dfrac{q^{2}}{C}\quad\text{ou}\quad E_{c}=\dfrac{1}{2}qu}$$
$E_{c}$ : en joules $(J)$
$C$ : en farads $(F)$
$u$ : en volts $(V)$
$q$ : en coulombs $(C)$
Ajouter un commentaire