Devoir n° 1 - Physique chimie - Ts

 

1) Un alcool saturé non cyclique dénommé $A$ a pour composition centésimale massique $68.2\%$ de carbone et $13.6\%$ d'hydrogène. 

 

Déterminer sa formule brute.

 

2) L'oxydation du composé $A$ par le permanganate de potassium en excès produit les composés $B$ et $C.$

 

$C$ donne une teinte rose au papier $pH.$ 

 

$B$, chauffé avec de la liqueur de Fehling, fait apparaître un précipité rouge, et par ailleurs précipite la $2.4-DNPH.$

 

a) Conclure sur la nature des produits $A$, $B$, et $C$

 

b) Donner les différentes formules semi-développées possibles de $A.$

 

3) Pour préciser la nature du composé $A$, on réalise l'addition d'une molécule d'eau sur un alcène $D.$

 

Cette réaction donne un produit majoritaire $E$ et également le composé $A$ minoritaire.

 

a) Sachant qu'un atome de carbone de $D$ porte trois liaisons simples carbone-carbone, donner les noms et les formules des composés $A$, $B$, $C$, $D$ et $E.$

 

b) Écrire l'équation de la réaction d'addition sur $D$ produisant $E.$

 

4) Dans un montage à reflux, on chauffe un mélange équimolaire de $A$ et d'acide éthanoïque. 

 

Dans le ballon, on a introduit $3.3\,mL$ d'alcool $A$ de densité $0.8.$ 

 

Après avoir stoppé la réaction, on dose l'acide éthanoïque restant dans le ballon par une solution d'hydroxyde de sodium de concentration $C_{b}=0.1\,mol\cdot L^{-1}.$ 

 

L'équivalence est atteinte pour un volume de base ajouté $V_{b}=150\,mL.$

 

a) Écrire l'équation de la réaction ayant eu lieu entre $A$ et l'acide éthanoïque.

 

b) Calculer le rendement de cette réaction.

 

c) Quelle est la masse du produit formé ?

 

d) La réaction a-t-elle atteint la limite communément admise pour une telle réaction ?

 

Données : 

 

masses molaires en $g\cdot mol^{-1}$ : $C$ : $12$ ; $O$ : $16$ ; $H$ : $1$

Au cours d'une séance de travaux pratiques, on réalise la synthèse d'un ester, l'éthanoate de pentyle, par deux méthodes, afin de montrer que le contrôle de l'évolution d'un système chimique peut s'effectuer par changement de l'un des réactifs.

 

La méthode $n_{01}$ consiste à faire réagir de l'acide éthanoïque avec une quantité stœchiométrique de pentan $-1-$ ol.

 

La méthode $n_{02}$ consiste à faire réagir de l'anhydride éthanoïque avec une quantité stœchiométrique de pentan $-1-$ ol.

 

a) Écrire les formules semi-développées de l'acide éthanoïque, du pentan $-1-$ ol et de l'anhydride éthanoïque. 

 

Entourer les groupes caractéristiques et nommer les familles des composés correspondantes.

 

b) Écrire les équations chimiques des deux réactions envisagées.

 

c) Déterminer les volumes d'acide carboxylique et d'anhydride d'acide, notés $V_{1}$ et $V_{2}$, nécessaires à la préparation d'un mélange stœchiométrique avec $50\,mL$ de pentan $-1-$ ol.

 

II. Sur le protocole de $TP$, on peut lire :

 

Méthode $n_{01}$ 

 

$-\ $ dans un ballon introduire $50\,mL$ de pentan $-1-$ ol, le volume $V_{1}$ d'acide éthanoïque calculé précédemment et $1\,mL$ d'acide sulfurique. 

 

Ajouter quelques billes de verre (ou pierre ponce) et chauffer à reflux pendant $1$ heure.

 

Méthode $n_{02}$ 

 

$-\ $ dans un ballon bien sec, introduire $50\,mL$ de pentan $-1-$ ol. 

 

Sous la hotte, verser, avec beaucoup de précautions et lentement, en agitant après chaque ajout, le volume $V_{2}$ d'anhydride éthanoïque calculé précédemment.

 

Ajouter quelques billes de verre et chauffer à reflux pendant $20$ minutes.

 

a) Quel est le rôle de l'acide sulfurique ajouté dans la méthode $n_{01}$ ?

 

b) Quel est le rôle des billes de verre ?

 

c) Pourquoi réalise-t-on l'expérience à chaud ?

 

d) Donner le schéma annoté du chauffage à reflux

 

III. Après refroidissement des deux ballons, on verse chaque mélange réactionnel dans de l'eau, on agite, puis on transvase dans une ampoule à décanter. 

 

Quelle que soit la méthode de préparation utilisée, on observe dans les deux ampoules deux couches de liquides non miscibles, dont l'une est l'ester. 

 

Après traitement de la phase convenable, on pèse la masse d'ester formée : 

 

méthode $n_{01}$ : $m_{1}=30\,g$ ; 

 

méthode $n_{02}$ : $m_{2}=52\,g$

 

a) Faire un schéma du contenu de l'ampoule à décanter dans le cadre de la méthode $n_{01}.$ 

 

On justifiera la position des deux phases.

 

b) Calculer le rendement dans chaque cas.

 

c) Quelle est la méthode la plus avantageuse en terme de rendement ?

 

d) Pour la méthode $n_{01}$, on peut éliminer l'eau formée du mélange réactionnel et ainsi obtenir l'ester avec un meilleur rendement. 

 

Justifier ce résultat en utilisant le tableau des données ci-dessous. 

 

Pour quelle raison le rendement est-il meilleur ?

 

Données:

$$\begin{array}{|c|c|c|c|} \hline &\text{Masse volumique en }g\cdot cm^{-3}&\text{Masse molaire}&\text{Température d’ébullition}\\ & &\text{moléculaire en }g\cdot mol^{-1}&TE\\ \hline \text{Pentan}-1-ol&0.81&88&118\\ \hline \text{Acide éthanoïque}&1.05&60&117\\ \hline \text{Anhydride éthanoïque}&1.08&102&\\ \hline \text{Ester}&0.87&130&143\\ \hline \end{array}$$

Une piste $ABCD$ est formée d'une partie $AB$ rectiligne qui fait un angle $\alpha$ avec la verticale, une partie $BC$ ayant la forme d'un arc de cercle de centre $O$ et de rayon $r$, et enfin une partie $CD$ verticale (voir fig). 

 

 

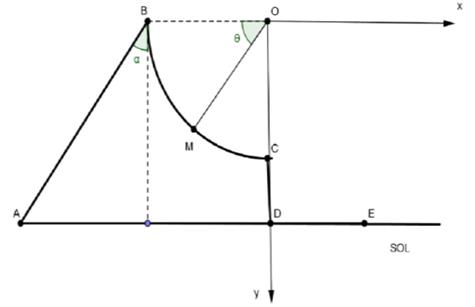
Données : 

 

$\alpha=60^{\circ}$, 

 

$g=10\,m/s^{2}$, 

 

$BO=CO=r=1m$, 

 

$OD=2m.$

 

Un solide S de masse $m=200\,g$ est lancé de $A$ vers $B$ avec une vitesse $V_{A}.$

 

1. Déterminer la nature du mouvement de $A$ à $B.$ 

 

Les frottements sont assimilables à une force $f=mg/4$ $($les frottements n'existent qu'entre $A$ et $B$ seulement$.)$

 

2. Calculer la vitesse minimale avec laquelle il faut lancer le solide $S$ du point $A$ pour qu'il arrive en $B$ avec une vitesse nulle.

 

3. Le solide $S$ descend de $B$ vers $C$ sans vitesse initiale.

 

3.1 Donner l'expression de sa vitesse en $M$ en fonction de $g$, $r$ et $(OB\;,\ OM)=30^{\circ}$

 

3.2 Trouver l'expression de la réaction $R$ en $M$ de la piste en fonction de $g$, $m$ et $8.$ 

 

La calculer.

 

4. Donner les caractéristiques de la vitesse du solide $S$ en $C.$

 

5. Le solide $S$ quitte la piste à $t=0$ et arrive au sol au point $E.$

 

6. Donner l'équation de la trajectoire du solide dans le repère $(O\ ;\ x\ ;\ y).$

 

Déterminer les coordonnées du point de chute $E.$

« Les personnages et les situations de ce récit étant purement fictifs, toute ressemblance avec des personnes ou des situations existantes ou ayant existé ne saurait être que fortuite.»

 

 

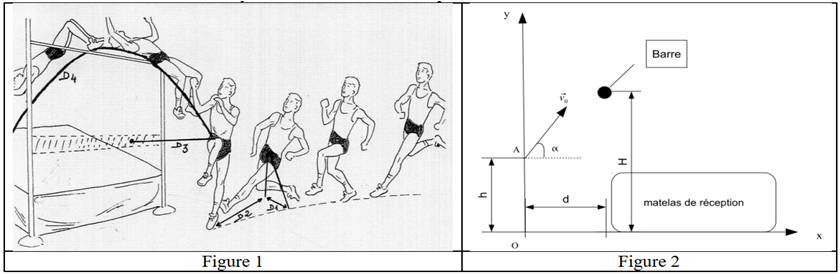
$-\ $ Afin d'améliorer son saut, l'athlète, qui suit des études en Terminale S, visualise grâce à une vidéo le saut effectué lors de son dernier entraînement Figure 1

 

$-\ $ Elle souhaite connaître la distance $d$ qui sépare son pied d'appel de l'aplomb de la barre pour éviter de retomber sur la barre ou de faire tomber la barre après le franchissement de celle-ci.

 

$-\ $ D'après ce qu'elle a vu dans son cours de physique, elle va essayer d'appliquer les lois du mouvement d'un projectile dans le champ de pesanteur.

 

L'angle entre le vecteur vitesse $\overrightarrow{V_{0}}$ et le plan horizontal du sol est noté $\alpha.$

 

Hypothèses simplificatrices proposées par son professeur de sciences physiques :

 

$-\ $ Les frottements avec l'air seront négligés

 

$-\ $ La poussée d'Archimède sera négligée.

 

$-\ $ Seul sera étudié le mouvement du centre de gravité $G$ de l'athlète.

 

$-\ $ Le mouvement du centre de gravité $G$ se fera dans un plan

 

$-\ $ Le champ de pesanteur est constant et égal à $g=9.80\,m\cdot s^{-2}.$

 

$-\ $ Le schéma de la situation est donné sur la figure 2 (l'échelle n'est pas respectée).

1) Préciser le référentiel à utiliser ainsi que le système.
 

2) En utilisant les hypothèses simplificatrices, quelle(s) est (sont) le(s) force(s) qui s'applique(nt) sur l'athlète ?

1) Rappeler à l'athlète l'énoncé de la deuxième loi de Newton.

 

2) En appliquant la deuxième loi de Newton, déterminer les équations horaires du mouvement de $G.$

 

3) Montrer que l'équation de la trajectoire peut se mettre sous la forme $y(x)=Ax^{2}+Bx+C.$ 

 

On donnera Les expressions littérales de $A$, $B$ et $C$ et on précisera leurs unités respectives (si elles existent).

La barre est placée à une hauteur $H=1.78\,m$ ; le centre d'inertie de l'athlète est tel que $h=1.00\,m$

 

L'angle $\alpha$ est égal à $60^{\circ}.$

 

1) Montrer que la vitesse initiale $V_{0}$ peut se mettre sous la forme que $V_{0}=\sqrt{\dfrac{2g(H-h)}{\cos\alpha}}$ 

 

2) Calculer la vitesse initiale $V_{0}$, d'abord en $m/s$ puis en $km/h$, dans les conditions indiquées.

 

3) La valeur trouvée pour la vitesse initiale est-elle aberrante ?

1) Montrer que la distance $d=\dfrac{2g(H-h)}{\tan\alpha}$

 

2) Calculer la distance $d$ pour $H=1.78\,m$ ; $h=1.00\,m$ et $\alpha=60^{\circ}$

 

3) La valeur trouvée pour la distance $d$ est-elle aberrante ?

1) Son entraîneur lui conseille d'éloigner sa prise d'appel de la barre quand celle-ci est placée plus haute.

 

L'expression précédente de $d$ confirme-t-elle ce conseil ?

 

L'athlète est-elle sûr de franchir la barre ? 

 

Que doit-elle modifier dans le cas contraire

Un faisceau d'électrons homocinétiques pénètre en $O$ entre les plaques horizontales $P$ et $N$ d'un condensateur plan, avec une vitesse initiale $V_{O}$ de norme $V_{O}=8\times 106ms^{-1}$ (voir figure ci-dessous). 

 

 

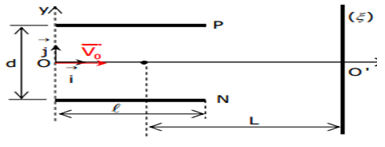
La tension entre les plaques est $U=V_{P}-V_{N}$, la plaque $P$ étant au potentiel le plus élevé

 

1) En appliquant le théorème du centre d'inertie, exprimé dans le repère orthonormé les équations horaires du mouvement d'un électron dans le champ. 

 

On négligera le poids de l'électron devant la force électrique.  

 

2) En l'équation de la trajectoire des électrons dans le champ et préciser sa nature

 

Quelle valeur maximale doit avoir $U$ pour que les électrons sortent du champ sans heurter les plaques ? 

  

3) Cette condition étant réalisée, on recueille les électrons sur un écran $(\mathfrak{C})$ placé à une distance $L=36\,cm$ du centre $I$ des plaques. 

 

Soit $Y$ l'ordonnée du point d'impact des électrons sur l'écran. 

 

Calculer le rapport  

 

4) Citer une application de la déviation d'un faisceau d'électron dans un champ électrique uniforme.   

 

Données : 

 

Distance entre les plaques : $d=5\,cm.$ 

 

Longueur des plaques : $l=10\,cm$

$$\text{Durée : }04\text{ heures}$$