Devoir n° 5 - Physique chimie - Ts2
Classe:
Terminale
Exercice 1 : Identification des solutions aqueuses
On prépare au laboratoire quatre solutions aqueuses ayant toutes la même concentration molaire : $C=10^{-2}mol\cdot L^{-1}$
$A$ : solution d'hydroxyde de sodium $NaOH$ ;
$B$ : solution de chlorure d'ammonium $NH_{4}Cl$ ;
$C$ : solution de chlorure de sodium $NaCl$ ;
$D$ : solution d'ammoniac $NH_{3}$
On remplit quatre flacons $($numérotés de $1$ à $4)$ avec ces solutions
Pour identifier le contenu de chaque flacon, on mesure le $pH$ de chaque solution
Les résultats sont regroupés dans un tableau
$$\begin{array}{|c|c|c|c|c|} \hline \text{Flacon }n^{\circ}&1&2&3&4\\ \hline pH&7.0&10.6&12.0&5.4\\ \hline \end{array}$$
1. Justifier la solution se trouvant dans chaque flacon.
Justifier le choix, pour chaque solution, à l'aide de l'équation-bilan de la réaction et justifier l'ordre de grandeur du $pH$ mesuré
2. Donner l'expression de la constante d'acidité du couple acide/base responsable du $pH$ de la solution $B$
Citer tous les couples acide/base présents dans la solution $B.$
3. Calculer la concentration des ions $H_{3}O^{+}$ de cette solution, en déduire la concentration des molécules d'ammoniac $NH_{3}$
4. Calculer le pourcentage $\alpha$ (coefficient de dissociation) d'ions ammonium en molécules d'ammoniac
On dilue $10$ fois la solution $B.$
Son $pH$ est égal $6.1$
5. Calculer la nouvelle concentration en ions $H_{3}O^{+}$ et la concentration des molécules d'ammoniac
6. Comment procéder pour préparer $100\,mL$ de cette solution diluée ?
7. Quelle est la nouvelle valeur du pourcentage $\alpha'$ d'ions ammonium transformés en molécules d'ammoniac.
8. Comparer $\alpha$ et $\alpha'.$
Quel est l'effet de la dilution sur l'équilibre chimique du couple $NH_{4}^{+}/NH_{3}$
On mélange $150\,mL$ de la solution $B$ avec $150\,mL$ de la solution $D$
9. Comment appelle-t-on une telle solution ?
Expliquer brièvement le comportement de cette solution.
Exercice 2
I. On mélange à $t=0$, dans un erlenmeyer un volume $v_{1}=50\,cm^{3}$ d'une solution aqueuse d'iodure de potassium $(K^{+}+I^{-})$ de concentration molaire $C_{1}$ avec un volume $v_{2}=100\,cm^{3}$ d'une solution aqueuse de peroxodisulfate de potassium $(2K^{+}+S_{2}O_{8}^{2-})$ de concentration molaire $C_{2}=0.1\,mol\cdot L^{-1}.$
La température maintenue fixe égale $25C^{\circ}.$
Il se forme le diiode $(I_{2})$ selon la réaction supposée totale d'équation chimique :
$$2I^{-}\ +\ S_{2}O_{8}^{2-}\ \rightarrow\ I_{2}\ +\ 2SO_{4}^{2-}$$
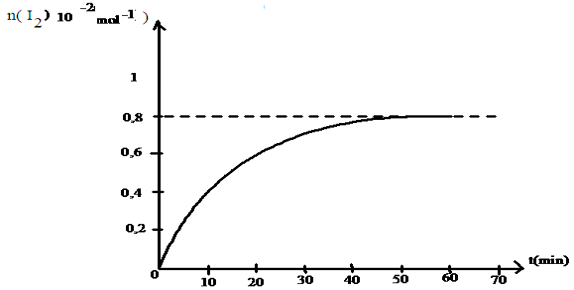
La courbe de la figure 1 représente la variation de la quantité de diiode $I_{2}$ en fonction de temps
1.1 Montrer alors que les ions $I^{-}$ est le réactif limitant.
1.2 En déduire alors la concentration molaire $C_{1}$ de la solution aqueuse d'iodure de potassium
2. En déduire la quantité de matière de chaque entité chimique présente dans le système à la date $t_{1}$
3.1 Définir la vitesse instantanée de la réaction.
3.2 Déterminer en expliquant la méthode utilisé les vitesses aux dates $t_{1}=20\,min.$ et $t_{2}=50\,min.$
3.3 Comment évolue cette vitesse de formation au du temps ?
Justifier la réponse
II. Dans le but d'étudier l'influence de certains facteurs cinétiques sur la vitesse moyenne de la réaction des ions $I^{-}$ avec les ions $S_{2}O_{8}^{2-}$, on réalise les expériences suivantes :
On considère trois béchers $(A)$ et $(B)$ et $(C)$, contenant chacun :
$-\ $ un volume $V_{1}=40\,mL$ d'une solution aqueuse $(S_{1})$ d'iodure de potassium $(K^{+}+I^{-})$ de concentration molaire $C_{1}=0.5mol\cdot L^{-1}$,
$-\ $ un volume $V'=10mL$ d'une solution diluée d'empois d'amidon.
$-\ $ un volume $V_{0}=0.5\,ml$ d'une solution aqueuse (s) de thiosulfate de sodium $(2Na^{+}+S_{2}O_{3}^{2})$ de concentration molaire $C_{0}=0.2\,mol\cdot L^{-1}.$
$\bullet\ $ Au contenu du bécher $(A)$, on ajoute quelques gouttes de sulfate de fer $II$,
$\bullet\ $ Au contenu du bécher $(B)$ on ajoute encore $20\,mL$ d'eau glacée.
$\bullet\ $ le bécher $(C)$ utilisé comme témoin
A l'instant $t=0$, on ajoute simultanément au mélange contenu dans chacun des trois béchers un volume $V_{2}=10\,ml$ d'une solution de peroxodisulfate de potassium $(2K^{+}+S_{2}O_{8}^{2-})$ de concentration molaire $C_{2}=0.05\,mol\cdot L^{-1}$ et déclencher aussitôt le chronomètre.
On note, pour chaque système chimique, la durée qui s'écoule entre l'instant initial et l'instant d'apparition d'une coloration bleue noire.
Les résultats sont consignés dans le tableau ci-dessous :
$$\begin{array}{|c|c|c|c|} \hline \text{bécher}&(A)&(B)&(C)\\ \hline \Delta\,t\ (min)&0.5&0.9&0.6\\ \hline \end{array}$$
1. En faisant appel aux calculs nécessaires et aux conditions expérimentales
a) Quels sont les différents facteurs cinétiques mis en jeu par ces trois expériences.
b) Préciser leurs influences sur la vitesse de la réaction ?
Exercice 3
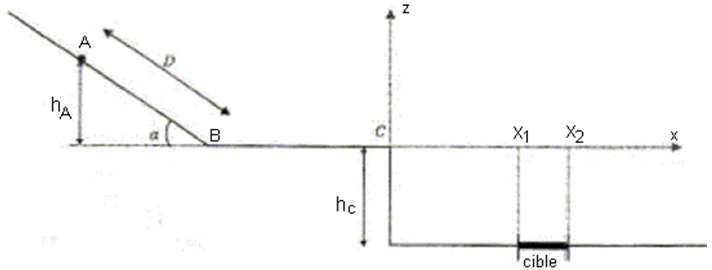
Le jeu schématisé ci-dessous consiste à placer un boulet sur un plan incliné de telle façon qu'il atteigne la cible.
Le boulet est tout d'abord lâché en $A$ sans vitesse initiale.
Le système étudié est le boulet assimilé à un point.
Toute l'étude est dans un référentiel galiléen.
On néglige les frottements.
$a=30^{\circ}$ ;
$D=AB=0.50\,m$ ;
$L=BC=0.20\,m$ ;
$h_{C}=0.40\,m$ ;
$m=10\,g$ ;
$g=9.8m/s^{2}.$
1. Étude du mouvement du boulet entre $A$ et $B$ :
1.1 Le système étudié est le boulet une fois lâché en $A.$
Faire l'inventaire des forces extérieures agissant sur le boulet.
Représenter ces forces sur un schéma sans soucis d'échelle.
1.2 On choisit l'altitude du point $C$ comme référence pour l'énergie potentielle de pesanteur $E_{pp}=0$ pour $z_{c}=0.$
$-\ $ Donner l'expression de l'énergie potentielle de pesanteur au point $A$ et vérifier qu'elle vaut $E_{pp}(A)=2.5\cdot10^{-2}J.$
$-\ $ En déduire l'expression puis la valeur de l'énergie mécanique du système au point $A.$
$-\ $ En déduire la valeur de l'énergie mécanique au point $B.$
Justifier.
1.3 Montrer que l'expression de la vitesse au point $B$ est $v_{B}=\sqrt{(2g\,D\sin\alpha)}.$
2. Étude de la chute du boulet après le point $C$ :
On étudie le mouvement du centre d'inertie $G$ du boulet après le point $C.$
L'origine des temps est prise lorsque le boulet est en $C.$
Le mouvement étant rectiligne et uniforme entre $B$ et $C$, la vitesse en $C$ est la même qu'en $B$ : $v_{C}=v_{B}=2.2\,m/s.$
2.1 On précise que l'action de l'air est négligée.
$-\ $ Énoncer la deuxième loi de Newton.
$-\ $ Appliquer cette loi au boulet lorsqu'il a quitté le point $C.$
$-\ $ Déterminer les composantes du vecteur accélération dans le repère $(C\;,\ x\;,\ z).$
2.2 Déterminer les composantes du vecteur vitesse dans le repère $(C\;,\ x\;,\ z).$
$-\ $ L'expression des composantes du vecteur position dans le repère $(C\;,\ x\;,\ z)$ est :
$$x=\sqrt{(2g\,D\sin\alpha)\cdot t}\ ;\ z=\dfrac{1}{2}gt^{2}$$
$-\ $ En déduire l'équation de la trajectoire donnant l'expression de $z$ en fonction de $x.$
2.3 On veut déterminer si le boulet atteint la cible $E$ dont l'abscisse est comprise entre $x_{1}=0.55\,m$ et $x_{2}=0.60\,m.$
$-\ $ Calculer le temps nécessaire pour que le boulet atteigne le sol.
$-\ $ En déduire l'abscisse $x_{S}$ du boulet lorsqu'il touche le sol.
2.4 Quelle distance $D$ faudrait-il choisir pour atteindre le point de la cible à l'abscisse $x_{S}=0.57\,m$ ? (la durée de la chute étant la même)
Exercice 4 : Radioactivité
On donne l'extrait de la classification périodique des éléments
$$\begin{array}{|c|c|c|c|c|c|} \hline \text{Symbole de l'élément}&Pb&Bi&Po&At&Ru\\ \hline \text{Numéro atomique }Z&82&83&Z&85&86\\ \hline \end{array}$$
1. Le nucléide de polonium $_{Z}^{210}Po$ est radioactif ; c'est un émetteur $\alpha.$
Sa désintégration donne le noyau fils $_{Z'}^{A'}X.$
Dans le noyau fils, le nombre de neutrons est égal à celui de protons $+42$
En indiquant les règles utilisées, déterminer $A'$, $Z'$ et $Z$
2. A une date origine $t=0$, un échantillon de polonium contient $N_{0}$ noyaux radioactifs
A une date $t$, on détermine le nombre $N$ de noyaux non désintégrés en évaluant le rapport.
On obtient les résultants :
$$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Date (en jours)}&0&40&80&100&120&150\\ \hline \dfrac{N}{N_{0}}&1&0.82&0.67&0.61&0.55&0.47\\ \hline -\ln\dfrac{N}{N_{0}}& & & & & & \\ \hline \end{array}$$
2.1 Définir la période radioactive $T$ d'un radionucléide.
2.2 Compléter le tableau avec les valeurs de $-\ln\dfrac{N}{N_{0}}$
2.3 Tracer la courbe : $-\ln\dfrac{N}{N_{0}}=f(t)$ ; avec $t$ en jours
Échelles :
$-\ $ en abscisse : $1\,cm$ pour $20$ jours ;
$-\ $ en ordonnée : $1\,cm$ pour $0.1$
3.1 A la date $t=T$, que vaut $-\ln\dfrac{N}{N_{0}}$ ?
En la valeur de la période $T$ du polonium
3.2 Établir en fonction de $T$ l'expression de la constante radioactive $\lambda$ d'un radionucléide
3.3 Calculer $\lambda$ pour le polonium et dire ce que cette constante représente pour la courbe précédente.
Exercice 5
I. En un point $M$ de l'espace se superpose deux champs magnétiques $\overrightarrow{B_{1}}$ et $\overrightarrow{B_{1}}$ créés par deux aimants dont les directions sont orthogonales.
Leurs intensités sont respectivement $B_{1}=3\cdot10^{-3}T$ et $B_{2}=4\cdot10^{-3}T.$
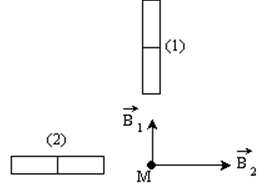
1. Déterminer les pôles des deux aimants.
2. Représenter graphiquement le champ résultant $\overrightarrow{B}$
3. Calculer $B$ et $\alpha=\left(\overrightarrow{B_{1}}\;,\ \overrightarrow{B}\right).$
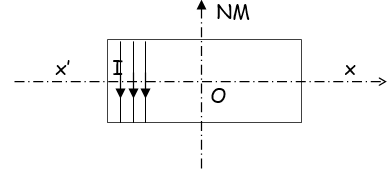
II. Un solénoïde d'axe $X'X$, de longueur $L=50\,cm$ et comportant $400$ spires est disposé de telle façon que son axe soit perpendiculaire au plan du méridien magnétique.
1. Déterminer l'angle de rotation $\alpha$ d'une aiguille aimantée mobile sur un axe vertical placée au centre $0$ du solénoïde lorsqu'on fait passer dans, ce dernier un courant d'intensité $I_{1}=0.04\,A.$
2. a) Déterminer l'intensité $I_{2}$ du courant qu'il faudrait faire passer dans le solénoïde pour avoir une rotation de l'aiguille aimantée d'un angle $\alpha=45^{\circ}$
b) Déterminer dans ce cas la valeur du champ magnétique résultant au point $O.$
3. Indiquer comment il faut disposer l'axe du solénoïde pour que l'aiguille aimantée ne tourne pas, lorsqu'on fait passer un courant dans celui-ci.
On donne :
$B_{h}=2\cdot10^{-5}T$
$\mu_{O}=4\pi\cdot10^{-7}(SI)$
$$\text{Durée }4h$$

Commentaires
ATIKPA (non vérifié)
dim, 09/06/2020 - 04:41
Permalien
Télécharger
DIOMANDE (non vérifié)
jeu, 02/18/2021 - 02:24
Permalien
BON SITE
GOUDIABY
mer, 04/05/2023 - 15:05
Permalien
Avoir le bac
WANIKO YAO APIN... (non vérifié)
ven, 05/09/2025 - 15:24
Permalien
Épreuves pour révision
Ajouter un commentaire