Dipôles passifs - 2nd S
Classe:
Seconde
I. Dipôles
1. Notion de dipôle
Un dipôle est un composant de circuit électrique qui comporte deux bornes ou pôles.
2. Catégorisation des dipôles
On distingue deux types de dipôles.
2.1. Les dipôles passifs
Un dipôle est dit passif s'il n'apparait aucune tension entre ses bornes lorsqu'il est branché seul aux bornes d'un voltmètre.
2.2. Dipôles actifs
Un dipôle est dit actif s'il apparait une tension entre ses bornes lorsqu'il est branché seul aux bornes d'un voltmètre.
3. Montage potentiométrique
3.1. Le Montage
Le potentiomètre est un conducteur ohmique qui possède d'une prise de tension intermédiaire variable.
Si on applique entre $A$ et $B$ une tension on obtient entre $B$ et $C$ une tension $U_{CB}$
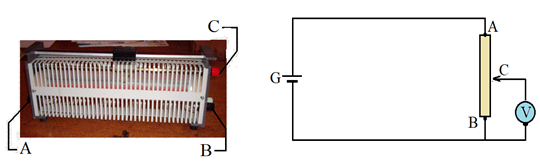
3.2. Utilisation du potentiomètre
On utilise le potentiomètre pour obtenir de tensions continues réglables
$-\ $ Tension entre $A$ et $B$
$U_{AB}=6V$ cette tension fixée par le générateur
$-\ $ Tension entre $C$ et $B$
$U_{CB}$ est une tension continue mais réglable.
Quand $C$ vient en $B\ $ $U_{CB}=0$
Quand $C$ vient en $A$
Les points $C$ et $A$ sont électriquement indifférents
$$U_{CB}=U_{AB}=6V$$
II. Dipôle passif linéaire
1. Étude d'un résistor ou d'un conducteur ohmique
1.1 Caractéristique d'un résistor
1.1.1. Définition
On appelle caractéristique d'un dipôle la représentation (très souvent expérimentale) d'une relation fonctionnelle entre deux grandeurs physiques.
En électricité quand les grandeurs sont la tension $U$ et l'intensité $I$
$-\ $ La caractéristique tension-intensité d'un dipôle est la courbe représentant les variations de l'intensité $I$ dans le dipôle en fonction de la tension $U$ à ses bornes $I=f(u)$
$-\ $ La caractéristique intensité-tension d'un dipôle est la courbe représentant les variations de la tension $U$ à ses bornes en fonction de l'intensité $I$ du courant qui le traverse.
1.1.2. Expérience
Montage
Considérons le montage suivant

Tracé de la caractéristique
En agissant sur le rhéostat $R_{h}$ on fait varier $I_{AB}$ lue sur l'ampèremètre pour chaque valeur de $I_{AB}$ on lit $U_{AB}$ sur le voltmètre.
Une expérience permet d'obtenir le tableau de valeurs suivantes
$$\begin{array}{|l|c|c|c|c|c|c|} \hline U_{AB}\;(V)&0&0.9&1.5&2.4&3.0&3.7\\ I_{AB}\;(mA)&0&30&50&80&100&123\\\hline \end{array}$$
Ce tableau nous permet de tracer la caractéristique intensité-tension
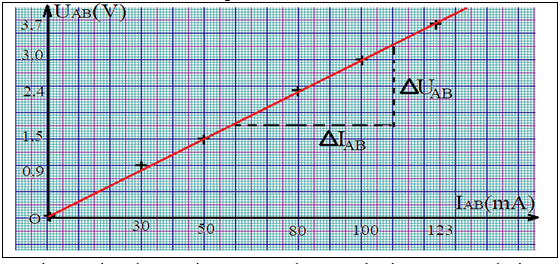
La caractéristique intensité-tension d'un résistor ou conducteur ohmique est une droite passant par l'origine limitée à la valeur maximale de $I_{AB}$ supportable par le résistor le résistor est un dipôle passif linéaire.
On obtiendrait la même courbe en intervertissant les bornes du résistor $U_{AB}=f\left(I_{AB}\right)$ le résistor est un dipôle symétrique.
Le coefficient directeur de la droite est appelé résistance noté $R$
La résistance électrique traduit la propriété des matériaux à s'opposer au déplacement des électrons.
Dans l'expérience décrite :
\begin{eqnarray} R &=&\dfrac{\Delta U_{AB}}{\Delta I_{AB}}\nonumber\\\\ &=&\dfrac{3.25-1.75}{(110-60)\cdot10^{-3}}\nonumber\\\\\Rightarrow R &=&30\Omega \end{eqnarray}
1.2. Loi d'ohm
Énoncé :
La tension appliquée aux bornes d'un conducteur ohmique est une fonction linéaire de l'intensité qui le traverse.
$$\boxed{U=RI}$$
Remarque :
La loi d'ohm s'écrit aussi
$$\boxed{I=GU\quad\text{avec}\quad G=\dfrac{1}{R}}$$
$G$ inverse de la résistance est appelé conductance et s'exprime en siemens $(S)$
1.3. Résistance d'un fil conducteur cylindrique et homogène
Soit un fil métallique de longueur $l$ et de section $S$
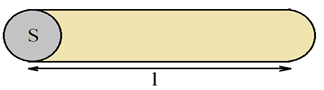
On démontre expérimentalement que la résistance d'un conducteur cylindrique et homogène est :
$-\ $ proportionnelle à sa longueur l
$-\ $ inversement proportionnelle à l'aire de sa section $\mathcal{S}$
$-\ $ variable avec sa nature et sa température selon un facteur s'appelle résistivité du conducteur
$$\boxed{R=\rho\dfrac{l}{S}}$$
$R$ en ohms $(\Omega)$ ; $l$ en mètres $(m)$ ; $S$ en mètres carrés $(m^{2})$ et $\rho=$ en ohms mètres $(\Omega m)$
Remarque :
L'inverse de la résistivité est la conductivité noté gamma s'exprime en siemens $(sm)$
2. Associations de dipôles ohmiques
2.1. L'association en série
Branchons-en série trois résistors de résistances

\begin{eqnarray} U_{AD}&=& U_{1}+U_{2}+U_{3}R_{1}I+R_{2}I+R_{3}I\nonumber\\\\ &=&\left(R_{1}+R_{2}+R_{3}\right)I\nonumber\\\\ &=& RI\nonumber\\\\\text{avec }R &=& R_{1}+R_{2}+R_{3} \end{eqnarray}
$R$ la résistance est équivalente qui permet de remplacer une association de plusieurs résistances.
Généralisation
Pour $n$ dipôles ohmiques différents en série la résistance équivalente est donnée par la relation
$$\boxed{R_{e}=\sum_{1}^{n}R_{i}}$$
Si les résistances sont toutes identiques alors
$$\boxed{R_{e}=nR}$$
1.2. L'association en parallèle
Branchons trois conducteurs ohmiques en parallèles entre deux points $A$ et $B$
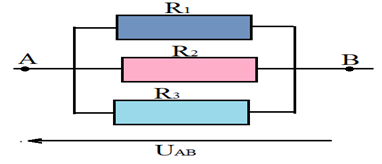
\begin{eqnarray} U_{AB}&=& R_{1}I_{1}\nonumber\\\\ &=&R_{2}I_{2}\nonumber\\\\ &=&R_{3}I_{3}\nonumber\\\\\Rightarrow I_{1} &=&\dfrac{U_{AB}}{R_{1}}\;, \end{eqnarray}
$I_{2}=\dfrac{U_{AB}}{R_{2}}\;,$
$I_{3}=\dfrac{U_{AB}}{R_{3}}\;,$
$\text{Or }I=I_{1}+I_{2}+I_{3}\\\\\Rightarrow I=\dfrac{U_{AB}}{R_{1}}+\dfrac{U_{AB}}{R_{2}}+\dfrac{U_{AB}}{R_{3}}$
\begin{eqnarray} &=&\left(\dfrac{1}{R_{1}}+\dfrac{1}{R_{2}}+\dfrac{1}{R_{3}}\right)U_{AB}\nonumber\\\\ &=& G_{1}U_{AB}+G_{2}U_{AB}+G_{3}U_{AB}\nonumber \\\\ &=&\left(G_{1}+G_{2}+G_{3}\right)U_{AB}\nonumber\\\\\Rightarrow G_{e}&=&G_{1}+G_{2}+G_{3} \end{eqnarray}
Pour trois dipôles ohmiques montés en parallèle la conductance équivalente est la somme des conductances
$$\boxed{G_{e}=G_{1}+G_{2}+G_{3}\Rightarrow\dfrac{l}{R_{e}}=\dfrac{l}{R_{1}}+\dfrac{l}{R_{2}}+\dfrac{l}{R_{3}}}$$
Généralisation
Pour $n$ dipôles ohmiques différents montes en parallèle la résistance équivalente est donnée par
$$\boxed{\dfrac{l}{R_{e}}=\sum_{1}^{n}\dfrac{l}{R_{1}}}$$
Si les résistances sont toutes identiques alors
$$\boxed{\dfrac{l}{R_{e}}=\dfrac{n}{R_{e}}\Rightarrow R_{e}=\dfrac{R}{n}}$$
III. Dipôles passifs non linéaires
1. Varistance $(V.D.R)$ (Voltage dépendant résistor) ou $(R.D.T)$ (Résistance dépendant de la tension)
1.1. Représentation symbolique d'une varistance
On représente une varistance par un rectangle barré la lettre $U$ indique que c'est une résistance dépendant de la tension

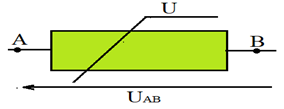
1.2. Caractéristique d'une varistance
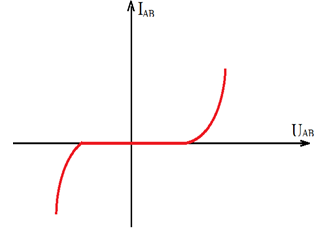
La caractéristique d'une varistance est symétrique par rapport à l'origine : la varistance est un dipôle passif symétrique.
Mais cette caractéristique n'est pas un dipôle linéaire : la varistance est un dipôle non linéaire
2. Diodes
2.1 Diode a jonction
Une diode a jonction (on dit souvent diode tout court) se présente sous la forme d'un petit cylindre de quelques mm de diamètre et portant d'un côté un anneau circulaire.
La borne d'entrée est du côté opposé à l'anneau la borne de sortie du même côté que cet anneau.
2.1.1. Représentation symbolique d'une diode à jonction

Cette représentation comme la diode n'est pas symétrique
Le dessin n'est pas le même quand on va de $A$ vers $B$ et quand on va de $B$ vers $A$
2.1.2. Caractéristique de la diode à jonction
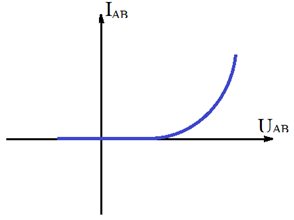
$-\ $ Une diode polarisée dans le sens direct sous une tension supérieure a $U_{s}$ est conductrice $I_{AB}\geq 0$ si $U_{AB}>U_{s}$
$-\ $ Une diode polarisée dans le sens inverse est non conductrice
$I_{AB}=0$ si $U_{AB}<U_{s}$
Remarque :
Une diode à jonction idéale a une tension de seuil nulle $U_{s}=0$
2.2 Diode Zener
2.2.1. Représentation symbolique d'une diode de Zener

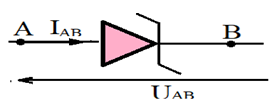
2.2.2. La caractéristique d'une diode de Zener
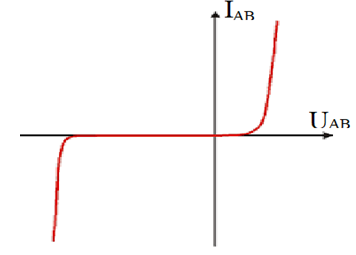
Une diode Zener est conductrice dans le sens direct si elle est polarisée dans le sens direct sous une tension supérieure à la tension de seuil $U_{s}$ $I_{AB}>0$ si $U_{AB}>U_{s}$
Une diode Zener est conductrice dans le sens inverse si elle est polarisée sous une tension inférieure à $-U_{z}$
$I_{AB}<0\quad\text{si}\quad U_{AB}<-U_{z}\quad\text{ou}\quad U_{BA}>U_{z}$
Une diode Zener est non conductrice si la tension a ses bornes est comprise entre $-U_{z}\leq U_{AB}\leq U_{s}$
Remarques :
Une diode Zener idéale a une tension de seuil nulle $U_{s}=0$
Un dipôle ne peut être utilisé dans n'importe quelle condition sans détériorer et rendu hors d'usage.
Le conducteur indique en générale une valeur limite de la tension de l'intensité à ne pas dépasser

Commentaires
Anonyme (non vérifié)
sam, 03/01/2025 - 19:37
Permalien
J'aime beaucoup le résumé du
Ajouter un commentaire