Vous êtes ici

Mouvement d'un solide sur un plan incliné - Ts

Classe:

Terminale

I. Rappels

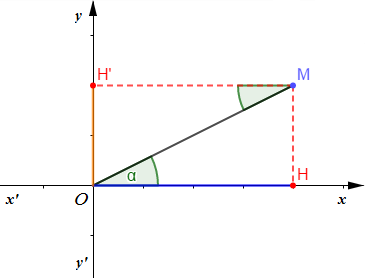
Considérons un repère orthonormé

$(O\;;\ \vec{i}\;,\ \vec{j})$ et soit

$M$ un point.

$H$ et

$H'$ sont les projetés orthogonaux de

$M$ respectivement sur les axes

$(x'x)$ et

$(y'y)$ alors on a :

$\left\lbrace\begin{array}{rcl} OH&=&OM\cos\alpha\\OH'&=&OM\sin\alpha\end{array}\right.$

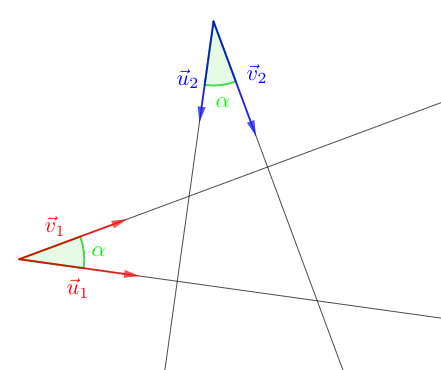
Soient

$\vec{u}_{1}\;,\ \vec{u}_{2}\;,\ \vec{v}_{1}\;,\ \vec{v}_{2}\;$ quatre vecteurs tels que

$\vec{u}_{1}\perp\vec{u}_{2}\;$ et

$\;\vec{v}_{1}\perp\vec{v}_{2}\;$ alors :

$mes\;\widehat{(\vec{u}_{1}\;,\ \vec{v}_{1})}=mes\;\widehat{(\vec{u}_{2}\;,\ \vec{v}_{2})}$

II. Mouvement sur un plan incliné

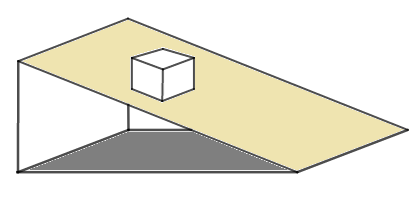
Illustration

Considérons une caisse de forme cubique, de masse

$m$ et de centre de gravité

$G$ , glissant sur un plan incliné d'un angle

$\alpha$ par rapport au plan horizontal.

Supposons qu'à l'instant

$t_{0}=0\;;\ \vec{v}_{0}=\vec{0}.$

Déterminons alors l'accélération et la vitesse de cette caisse à un instant

$t$ quelconque.

Étude du mouvement

$\centerdot\ \$ Le système étudié est la caisse, considérée comme un solide ou un point matériel.

$\centerdot\ \$ Le référentiel d'étude est le référentiel terrestre supposé galiléen.

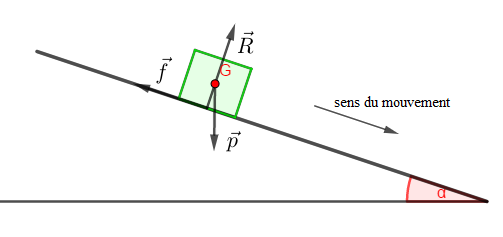
$\centerdot\ \$ Les forces extérieures appliquées au système sont :

$-\ \$ Le poids

$\vec{p}$ ; force exercée par la terre sur la caisse.

$-\ \$ La composante normale

$\vec{R}$ de la réaction du plan incliné sur la caisse.

$-\ \$ La force de frottement

$\vec{f}$ toujours colinéaire et opposée au sens du mouvement.

$\centerdot\ \$ Appliquons le théorème du centre d'inertie ou principe fondamental de la dynamique. On obtient alors :

$\sum \vec{F}_{\text{ext}}=m\vec{a}_{_{G}}=\vec{p}+\vec{f}+\vec{R}$

$\centerdot\ \$ Choisissons comme repère de projection un repère orthonormé

$(O\;;\ \vec{i}\;,\ \vec{j})$ et supposons qu'à l'instant

$t_{0}=0$ , le centre d'inertie

$G$ du solide, considéré comme un point matériel, se trouve à l'origine

$O$ du repère.

$\centerdot\ \$ Projetons la relation

$\ \vec{p}+\vec{f}+\vec{R}=m\vec{a}_{_{G}}$ sur les axes du repère.

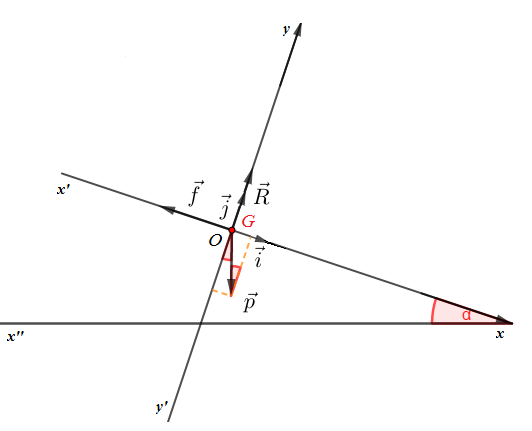
Les expressions des vecteurs

$\vec{f}\;,\ \vec{R}\;,\ \vec{a}_{_{G}}$ et

$\vec{p}$ dans la base

$(\vec{i}\;,\ \vec{j})$ sont alors données par :

$\vec{f}\left\lbrace\begin{array}{rcr} f_{x}&=&-f\\f_{y}&=&0\end{array}\right.\;,\quad\vec{R}\left\lbrace\begin{array}{rcr} R_{x}&=&0\\R_{y}&=&R\end{array}\right.\;,\quad\vec{a}_{_{G}}\left\lbrace\begin{array}{rcl} a_{_{G_{x}}}&=&a_{_{G}}\\a_{_{G_{y}}}&=&0\end{array}\right.$